英国《数学教学》中的数学文化活动分析

唐恒钧, 蒋逸卿, 郑蓉蓉

(浙江师范大学 教育学院,浙江 金华 321004)

0 引 言

当前,数学文化的教育价值已被越来越多人认可,数学文化也逐渐成为数学课程与教学的重要组成部分.《普通高中数学课程标准(2017版2020年修订)》[1](以下简称《课标》)强调“数学文化应融入数学教学活动,教师应有意识地结合相应的教学内容,将数学文化渗透在日常教学中”,并明确指出数学文化融入和渗透数学教学有重要的数学教育作用.在课程标准的引领下,数学文化融入课堂教学已成为数学教育研究的一个热门话题,然而教师在教学实践中普遍感到数学文化素材不够丰富,且可推广应用的研究成果也比较欠缺[2-3],从国际比较视野下考察如何融入、如何处理数学文化素材的研究也相对较少.

英国也高度重视数学文化的教育价值.英国国家数学课程标准(2000)在“数学的重要性”中充分揭示了数学应用过程的文化相关性[4];英国2014版数学课程标准强调数学是人类优秀文化中的重要组成部分,认为学生需要了解一定的数学发展历史和数学文化,对于文化的理解和认同是发展学生核心素养必不可少的部分[5].

英国数学教师协会(Association of Teachers of Mathematics,简称ATM)出版发行的刊物《数学教学》(《Mathematics Teaching》)创刊于1956年,主要面向中小学数学教育.该期刊对学生的数学文化体验有持续性的关注,长期以论文、讲座报告、论坛记录等多种形式呈现数学教育工作者丰富的数学文化活动的设计构想或实施经验,在英国中小学数学教师界有着广泛而深刻的影响.《数学教学》近年刊发的数学文化类论文中,有哪些值得推广应用的数学文化活动素材?它们有怎样的主题和特色?英国数学教师又是如何处理、运用这些素材的?基于上述问题,本文对该刊近5年所发表的数学文化类论文进行统计和分析,旨在为我国中小学数学教师提供有应用价值的数学文化素材,为数学文化素材的处理、数学文化融入教学提供借鉴.

1 《数学教学》中的数学文化内容

为明确研究对象,选择《数学教学》近5年(2018—2022年)主要内容涉及数学文化方面的论文(数学史类论文不做统计),排除重复论文(多期连载论文分别计次),最终统计得到130篇论文.借鉴林佳乐等[3]的分类框架,将所得论文分为“专题研究”与“教学活动”两大类.“专题研究”是对某个数学文化主题的讨论,共25篇,一般不涉及主题的教学转化.比如Jones[6]呈现了他从发现“素数平方之差为12的倍数”这一规律开始,展开对素数之数学美、与音乐交融之美的自我探寻过程.“教学活动”是作者设计的以数学文化为主题的活动,共105篇,大部分已在课堂中实施.比如,Williams[7]设计了以“计数”和“测量”为主题的活动.活动之一是教师给出一系列粘贴了垂直胶纸带的不同的透明容器,让学生用一个小罐子往容器中倒入一罐水并在胶纸带上进行标注,用来比较各容器的容积大小.图1给出了2018—2022年数学文化教学活动类论文的逐年数量分布情况.

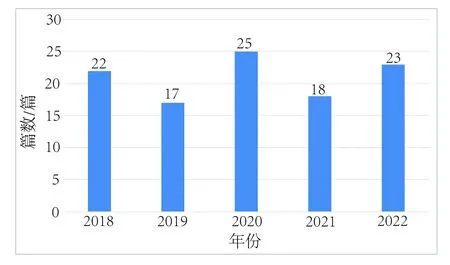
图1 《数学教学》近5年数学文化教学活动论文的数量分布

从图1不难发现,近年来《数学教学》对数学文化教学活动的重视程度较高且呈稳定的态势.值得一提的是,自2020年第271期开始,该刊推出了“Insight”栏目,此后的每一期几乎都会在这一栏目中发布特邀艺术家针对具体数学内容所进行的艺术创作,它们或是数学思维的艺术表达,或是代数内容的可视化加工,或是可用于教学的几何图案设计,呈现了丰富多彩的数学文化素材,这也从一个侧面反映出该刊对数学文化教学活动的重视.

按照不同的主题,近5年105篇数学文化教学活动论文大致可分为5类:数学与自然科学、数学与人文科学、数学与生活、数学与游戏、数学与技术.下面对这5个类别依次介绍和分析.

1.1 数学与自然科学

1.1.1 数学与天文

Johnstone[8]设计了关于“星际穿越—时间旅行”的探究活动.活动中教师首先引发学生对光子在星际间进行时间旅行的思考:正照射到地球的点点星光在其刚出发之时,地球上正发生着什么呢?此时与那束光出发的那一刻是否有某种浪漫的联系?接着让学生选择一个天体(比如金星)以及对于自己而言特殊的一个日期,借助天象模拟软件Stellarium,绘制天体在该日期的位置,找到并点击指定日期离金星最近的恒星,获得该恒星到地球的距离数据,计算该恒星发出的光刚启程时地球所处的时间.整个活动中,学生被深深吸引,不断尝试输入不同的特殊日期进行计算,体会过去与现在若有若无的浪漫联系,这在提高数学运算能力的同时,也能引发运算与实际结合的思考,比如计算日期时需考虑闰年等因素.

1.1.2 数学与物理

Ashton[9]设计了一个借助空气浮力和天平平衡原理来帮助学生理解含有负数的一元一次方程的实验观察活动.教师发现对于负整数作为系数或常数项的方程,如 10-x=7,x-5=11,不管是在教学上还是学生理解上都比较困难.为此,教师使用天平和气球,利用气球的浮力将负数直观地呈现在天平的平衡状态当中(见图2和图3),引导学生观察记录并尝试自己动手操作构造方程.该设计克服了原有用天平平衡原理去理解涉及负整数作为系数或常数项的方程的困难,学生的应用意识和问题解决能力也能在这个过程中得到提升.

图2 负整数作系数的方程的直观化 图3 负整数作常数项的方程的直观化

1.1.3 数学与生物

有学者设计了有关新冠肺炎平面传染动态模型的探索活动[10].教师将实际问题简化,虚构了一种通过空气传播的传染病,规定其传染半径为2 m,学生的任务是随机绘制5条直线路径(人们可以沿着直线路径移动,越来越多的人一起移动则会产生路径的重叠,比如排队等候的时候),建构相关位点,评估潜在的传播点,如图4所示.活动的目的是让学生认识到数学广泛的应用价值,学会用

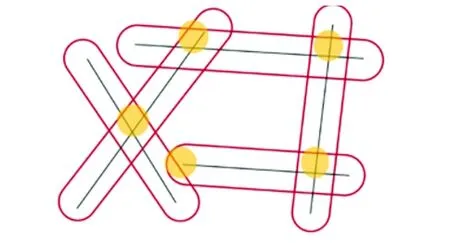
图4 传染病的传播路径

数学的眼光和思维去认识、思考现实生活中的问题,以此培养应用能力及批判质疑精神.

1.2 数学与人文科学

1.2.1 数学与文学

Thompson等[11]借助哈利·波特和隐形斗篷的故事背景设计了一个计数活动以支持学生理解负数的加减法.教师与学生商定:巫师的个数代表正数,负数则由隐形斗篷来表示.教师让学生借助此规则,尽可能多地构造正向和反向的例子.例如,正向的例子“用此规则解释‘4-3’的意义”;反向的例子“用数的加减法算式刻画‘有5个巫师,其中2个穿上了隐形斗篷’”.又比如,对于“4+3”“4-3”“(-4)+(-3)”的含义,第1个指“原有4个巫师,又来了3个巫师后的总数”,第2个表示“原有4个巫师,3个巫师穿上了隐形斗篷后,可见的巫师总数”,第3个表示“原有4件隐形斗篷,再添加3件后的总数”.当有学生提出负数减法的例子,尤其是被减数大于减数时,教师让学生小组探究,结合画图、实物模型操作等方式,借助上述故事背景分析其中的含义.比如,“(-2)-(-7)”可以这样理解:所有的巫师都穿上了隐形斗篷后,还有2件隐形斗篷剩余,现在有人拿走7件斗篷后,我可以看到多少巫师.他们通过课后的调查反馈发现,这样的探究活动得到了许多学生的认可与喜爱,并且有效突破了负数减法的难点,促进了学生的理解.

Jenny等[12]用“Alien′s love underpants”的故事和学生一起探索外星人内裤的测量问题.教师根据故事设置情境:一条巨大的内裤被遗弃在学校的操场,上面写着“请参考外星人裤子尺寸表找到裤子的主人”.接着教师组织学生进行测量的探究,学生主要经历了“测量工具的选择”“度量单位的统一”“测量与数据的收集”“比对并得出结论”4个环节,收集了一系列故事中外星人身体尺寸的数据,通过比对,最终找到了裤子的主人.整个活动中,学生都表现得十分兴奋,在合作、交流、探究中解决问题,树立了用数学探究的信心.

1.2.2 数学与艺术

Knoll[13]设置了“颜色调配”的数学探索活动.教师首先介绍了色彩混合的原理,提出如何通过调配颜色的混合来精准控制混合后的颜色的问题.学生借助图表,记录不同比例的原色墨水混合后产生的色调,深入探究一系列原色墨水混合比例与产出颜色的变化关系.他们认为这是整合数学与艺术的有益探索,在问题解决过程中深入学习比例的知识,促进了学生对知识的理解,培养了学生的数学核心素养.

Charlotte[14]介绍了伊斯兰几何融入数学课堂的例子.首先,向学生展示伊斯兰几何中主要由三角形、六边形、十二边形和这些形状的倍数构造而形成的“六倍图案”(见图5和图6),进而介绍了构造这种图案的基本方法.在了解构造的几种方法后,进一步让学生自主创作以六倍图案为载体的伊斯兰几何图案并分享创作成果.他们认为伊斯兰几何图案的创作活动融合了数学、艺术和历史的元素,能够提高学生几何推理的能力,培养合作探究的意识与能力.

图5 伊斯兰几何六倍图案(一) 图6 伊斯兰几何六倍图案(二)

1.3 数学与生活

1.3.1 数学与个人生活

Barbara母子俩[15]设计了一个年龄数字与几何图形相结合的数学活动,其灵感来源于Derek为庆祝母亲Barbara100岁生日所制作的贺卡中的有趣图案.教师首先呈现出这种贺卡图案的设计思路(见图7),数字64表示母亲第1次见Derek时的年龄,36表示母亲和Derek在一起的时间,82+62=102正好是母亲现在的年龄.在理解图案的设计思路后,学生进行小组合作,为家庭成员设计制作类似的卡片图案,并在课堂上进行展示.各组学生讨论和推测所展示的图案代表年龄的大小.在这样制作与互动的过程中,学生能够吸取各方意见及时调整原有的图案,反思其中的数学方法,充分发挥自身的数学创造力.

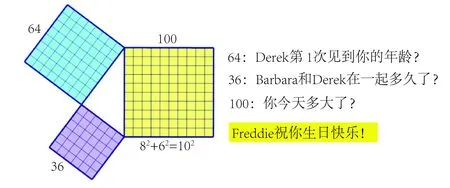
图7 贺卡图案

Cotton[16]设计了“虚拟假期”和“这东西有多大”的活动.在第1个活动中,教师让学生选择一个他们想去的地方并制定一个虚拟的假期计划.计划中包括交通工具的选择、时间的安排、住宿及景点规划等等,最后查询相关信息确定旅行的费用.如果目的地与本地使用的货币不同,则还需确定两地货币的汇率关系,以便准备足够的货币进行兑换.在第2个活动中,学生需要整理众多书籍,教师让学生测量所有书籍的长度、重量,并寻找合适的容器来装这些书,这个活动可以发展学生的量感以及测量的意识.

1.3.2 数学与社会生活

Archer等[17]将气候危机的问题引入课堂,让学生探究应用数学方法减少学校碳排放,实现碳中和的方案.学生被分成若干个小组,每个小组拥有50万英镑的预算,教师给出了5个可能的方案并依次介绍,50万英镑的预算最多只能选择一个方案实施,每个小组需要制定标准(如每千磅减少的碳排放量)以判断5个方案的优劣,从而做出选择.在第2个任务中,学生被要求将剩下的预算用于购置太阳能板,教师提供了2家公司所售太阳能板的基本参数,每个小组需要商讨确定选择哪个公司的太阳能板并给出理由.这个活动能够让学生感受到数学在现实世界中所扮演的角色,体会数学是帮助人们理解世界、改造世界的有力工具.

Coles等[18]以博茨瓦纳降雨量变化的预测为情景,设计了教学活动,旨在让学生将学习过的平均数、中位数、众数等数学知识应用于现实问题的解决中.教师介绍博茨瓦纳的基本情况,并给出了使用9种气候模型预测博茨瓦纳未来降雨量变化的结果(如表1所示).学生被要求利用这组数据写一份书面报告来告知博茨瓦纳的农民未来气候变化和存在的风险.在处理表1的数据时,学生采取了不同的方法,具体有计算平均数、众数、中位数等.在讨论中,学生发现采用不同的方法所得到的预测结果很不相同,比如使用平均数就抵消了变化而显示出较小的波动,使用众数则显示未来降雨量的减少.通过使用真实的数据和模型,学生可以体会到数学工具对气候预测的影响,感受到气候变化的不确定性和气候预测的复杂性.

表1 博茨瓦纳降雨量预测

1.4 数学与游戏

Shaw[19]设计了“手指数学”的教学活动以帮助学生学习乘法表.规则如下:从小拇指到大拇指依次记为6,7,8,9,10(见图8).以7×8为例,将记为7的手指和记为8的手指抵在一起(见图9),这2根手指及其下面的手指每根计10,产生 50,用剩余的手指,一只手上的手指数乘以另一只手的手指数,然后得到3×2=6,最后将2个结果相加给出最终答案为56.

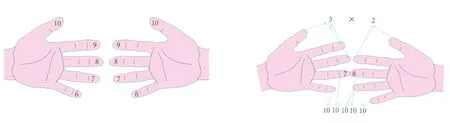
图8 手指的编号 图9 “手指数学”计算的过程

Huntley[20]将一种名为“三振出局”的游戏引入课堂以提升学生的数学运算能力.教师首先给出一行0～20的数列,要求学生选择数列中的3个数字用加法或减法组成算式.例如选择4+3=7,那么学生需要把4和3划去并把7圈起来.在紧接着的下一轮,对手必须以前一轮的运算结果开头做出算式,比如 7+11=18.之后便重复先前的操作即可,要注意的是算式中另外2个数必须选择尚未使用过的数字.随着数字的减少,算式构造也会逐渐变难,直至一方不能用余下的数字构造出合理的算式时,另一方就获胜了.

1.5 数学与技术

Vos等[21]将桑基图运用到课堂教学之中.教师首先以挪威牛奶制造商年度报告中的真实数据为例,绘制并介绍了桑基图.接着学生分组完成教师分发的任务卡片上的问题,这些问题都与上述牛奶加工的桑基图相关,使学生加深对桑基图的理解和认可.在学生对桑基图有一定程度的了解后,教师便让每个小组选择自己感兴趣的主题进行桑基图的创作.他们认为,桑基图为数学和社会学科的交叉、融合提供了载体,能够很好地培养学生在复杂的社会情境中提取信息、分析数据并进行推理的能力.

Rumbelow等[22]探讨了影视制作技术在数学课堂中的应用并进行了实践.该教学活动的主题为“对自然现象的建模”,教师先让学生借助视频剪辑软件创建海浪运动的视频,然后使用动态几何软件(如Geogebra)制作曲线的动画模型,最后结合视频剪辑软件进行美化形成个人的建模作品.这项活动表明,在自然界中捕捉优美的动态短片,并与图形化的动态数学模型相结合,可以拓展对自然与数学之美的欣赏方式,提高审美情趣.

2 数学文化活动的特点

通过对《数学教学》近5年数学文化活动论文的分析,总结得到如下5个方面的特点:

第一,主题丰富,形式多样.《数学教学》中的数学文化活动主题异彩纷呈,涵盖了数学与自然科学、数学与人文科学、数学与生活、数学与游戏、数学与技术等多个领域,且每一类主题之下还包含各具特色的子类.这些主题绝大部分源于生活,与现实联系紧密,在激发学生探究兴趣、提升探究本领方面效果显著.此外,数学文化活动中,任务的形式也各具特色,有的为博茨瓦纳农民撰写书面报告来告知气候的变化和风险[18],有的创作伊斯兰几何图案的艺术作品[14],有的替学校设计碳中和实施方案[17],有的用数学知识创作音乐作品[23].多样化的任务形式为数学课堂注入无限活力,学生能够在做中学,在学中做,在做中创.

第二,聚焦现实,与时俱进.《数学教学》中的许多数学文化活动主题关注社会热点,与时事紧密相关.考察2020年以来的论文便能发现不少以新冠疫情为背景的活动设计,如以传染病模型为主题的教学活动、适用于线上教学模式的数学游戏、关注全球生态环境问题的活动计划等.

第三,活动设计倡导合作,主体多元化.在数学文化活动的设计上,提倡活动设计的主体多元化,倡导理论研究者、专业技术人员与教育实践者的通力协作.如博茨瓦纳降水预测的教学活动由Coles(数学教育学教授)、Daron(应用气象科学家)、Rolph(中学数学教师)合作设计实施;桑基图的教学活动则由数学教育学教授Vos和数学教师Omobude协作完成.上述例子甚多,此处不再一一枚举.

第四,重视情境,体验真实.在情境的运用方面,尤其关注情境的真实性.例如在桑基图的教学活动中,教师选用了牛奶制造商年度报告中的真实数据绘制桑基图;在文献[10]中设计者采用了出生率与死亡率、性别平等、全球变暖等真实情境设计活动.基于真实情境设计的活动能够引导学生主动探索知识,提高解决社会生活实际问题的能力.

第五,技术介入,深度融合.在设计与实施活动时重视信息技术的融入.除了最基本的使用动态几何软件直观呈现知识、丰富课堂互动外,数学文化活动设计还重视用信息技术支持数学建模和探究活动的开展,支持学生之间的交流合作.比如上述海浪运动建模的例子中,学生从海浪短片的捕捉到模型的建立再到最后成品的制作,活动全程都在Geogebra,iMovie等软件的支持下进行,借助信息技术对大自然进行建模并创作电影,为学生创造力的发展提供了来源、动力及技术保障.

3 启示与反思

基于对《数学教学》中数学文化活动论文内容及特点的分析,发现其中存在不少值得借鉴的方面.

3.1 数学文化素材的选择与处理

《数学教学》所体现的英国数学课堂中的数学文化活动,其主题与形式丰富多样且往往聚焦时下,创设贴近学生生活的真实情境问题,以问题解决为导向贯通数学与现实,可以让学生体会到数学的广泛适用性,加深对数学的理解.当前我国数学文化的教学设计呈现出片段式、问题情境式、一课一评式和专题研究式等4大类[24],在形式类型、深入程度等方面相较于以前都取得了一定的发展,但设计难度依旧很大,创新的尺度、融合的深度仍是需要持续探索的话题.在选取素材、设置驱动性任务并组织教学活动时,需要考虑以下几个方面:首先,素材所提供的任务(问题)是否有真正的意义.即,是否能真正驱动学生探索,让学生迫切想知道答案.其次,素材背景与学生生活现实的相关性.选取素材时需要考虑素材背景下所能设计的问题与活动是否与学生有内在的关联性.再次,数学是否真的有助于问题的解决.即,使用数学的思想方法去解决问题是否比其他方法更容易、更有效.最后,素材所提供的任务(问题)是否能促进更广泛、更持久的讨论.学生能否意识到课堂活动中解决的问题只是真实问题解决过程中的一部分,问题解决永远处于进行时.

因此,在素材的选择与处理时,可以选取与学生的生活经验相联系且具有他们可识别价值的素材;设计驱动性问题时要对素材适度加工,以凸显数学问题解决的实际意义以及数学思想方法的独特优势;教师对素材需要有深刻理解,设计的问题应具有延展性以促进学生更广泛而深刻地思考,从而彰显数学文化的教育价值.

3.2 合作研究模式的实现方式

《数学教学》中数学文化活动论文呈现出高校数学文化和数学教育的理论研究者与一线数学教师紧密合作的特点.不仅如此,其中不少案例还包括特定领域专业技术人员的全面参与.这种合作研究模式是如何形成的?以文献[18]的活动为例,数学教育理论研究者与气象专家共同制定了课堂实施的整体框架,其中课堂任务来源于气象专家的研究课题,一线教师丰富完善了实施细节并进行了教学实践.教学活动中,数学结果所反映的实际意义学生可能无法自主解读并完全理解,气象专家则提供了专业的说明.在3个层面主体的协作下,活动任务获得了真实数据的进一步支撑,实施形式得到了进一步的丰富,实施效果能够及时被科学评估.因此,开发主题丰富、设计科学、内容生动的数学文化活动,需要数学教育理论研究者以及专业技术人员与一线教师的通力协作,这样才能产出更多有推广应用价值的研究成果.

3.3 信息技术的介入与运用

信息技术在《数学教学》所呈现的英国数学课堂的数学文化活动中,充当了学生进行数学探索和发现的工具.比如学生借助动态几何软件(DGS)对折纸进行建模,在此过程中探索、发现并应用几何性质[25];使用Excel随机生成具有特定结构的方程,通过对大量随机方程的观察和探讨促进对数学本质的抽象与理解[26].事实上,信息技术作用于教育的过程与效果的认识是信息技术融入教学的关键,在信息技术支持下开展数学文化活动,学生在其提供的丰富资源和多样方法中自主探索、主动学习,信息技术的融入助推数学文化与数学教学真正融合为一体.