均匀弹性杆弯曲振动的机电等效电路

李凤鸣, 刘世清, 许 龙, 陈赵江

(1.浙江师范大学 应用声学研究所,浙江 金华 321004;2.中国计量大学 理学院,浙江 杭州 310018)

0 引 言

板、梁或杆是机械振动及土木建筑等结构工程中的重要构件.在超声学特别是功率超声领域,杆形或盘形变幅器,如等截面杆、锥形和指数形变截面杆及各种剖面形状的盘形振子等[1-5],作为功率超声换能器振动系统的重要组件,一方面能起到振幅放大作用,以提高振子声能辐射效率;另一方面具有阻抗变换功能,以实现换能器与负载之间的阻抗匹配,提高声能传输效率.由于压电超声换能器是一种复杂的机电耦合振动系统,其理论设计常采用机电类比等效电路法进行分析.与传统解析法相比,等效电路法在分析处理振动问题、特别是机电耦合系统的振动问题时尤为便捷,求解过程及物理意义更加直观明了.

弹性振子的振动模式主要包括纵向、扭转、弯曲及径向几种单一振动模式,以及纵扭、纵弯、纵径等几种复合振动模式.目前,对于杆或盘形振子的纵向[6-7]、扭转[8-9]及径向[10-14]等几种单一振动模式的机电等效电路研究较多,且已比较完备,而对弯曲振动模式机电等效电路的研究相对比较欠缺,其振动分析基本上仍采用经典解析理论方法.文献[15-16]利用传递矩阵法推导出弯曲模式超声变幅杆的特性参量表达式;文献[17]分别基于4种梁理论,利用解析法对超声变幅杆的弯曲振动频率特性进行了数值计算与分析.

本文基于弹性力学理论与机电类比原理,以经典Shear梁和Euler-Bernoulli梁为研究对象,结合边界条件,推导了均匀截面杆形振子弯曲振动的机电类比等效电路,并在等效电路基础上得出了共振频率方程.探讨了矩形截面均匀弹性杆几何尺寸对其各阶次弯曲共振频率的影响,并进行了有限元数值计算和验证.

1 均匀弹性杆弯曲振动分析

在振动力学中,受横向载荷的杆亦称梁,梁和杆均属于一维结构.设一均匀弹性杆形振子的两端所受横向力分别为F1和F2,振动速度分别为υ1和υ2,弯矩分别为M1和M2,如图1所示.由振动理论可知,弹性杆在弯矩作用下将产生横向弯曲振动.以下将依据弹性梁理论与机电类比原理,并结合相应的力学边界条件,得出杆两端力与质点振速的关系,进而得出其弯曲振动机电类比等效电路及共振频率方程.

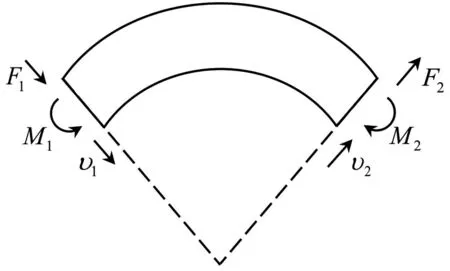
图1 杆元段的力学分析

2 均匀弹性杆的弯曲振动机电等效电路

2.1 Shear弹性梁

对于均匀截面弹性Shear梁(杆),在无激励条件下,其动力学方程[18]为

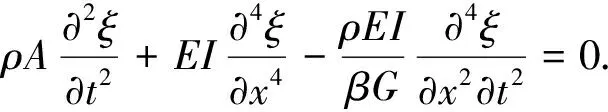
(1)

式(1)中:ξ(x,t)为杆的横向位移;ρ为材料密度;A为杆的横截面积;E为弹性模量;I为惯性矩[截面为矩形时,I=wh3/12(w为矩形截面宽度,h为矩形截面高度),截面为圆形时,I=πr4/4(r为圆截面半径)];β为与截面形状相关的剪应力系数(矩形截面为5/6,圆形截面为9/10);G=E/[2(1+σ)]为剪切弹性模量;σ为泊松比.由式(1)得杆的横向位移通解为

ξ(x,t)=[a1cos(kx)+a2sin(kx)+a3cosh(λx)+a4sinh(λx)]exp(jωt).

(2)

式(2)中:a1,a2,a3和a4均为积分常数,由边界条件确定;k和λ的表达式分别为:

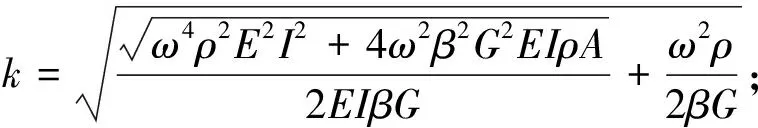
(3)

(4)

式(3)和(4)中,ω=2πf为角频率.

由式(2)可得杆的横向弯曲振动速度、弯矩和横向力分布函数分别为:

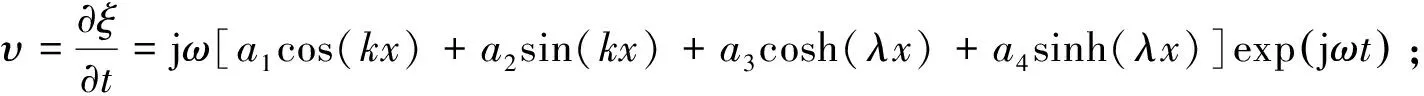
(5)

(6)

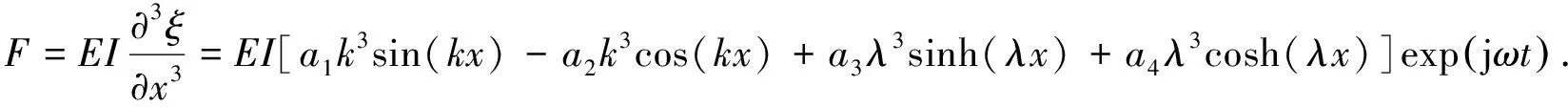
(7)

对于长为l、两端自由的均匀弹性杆,其两端弯矩均为0.图1所示的边界条件为:当x=0时,υ=υ1,F=F1,M=M1=0;当x=l时,υ=-υ2,F=F2,M=M2=0.各力学参量的具体表达式分别为:

υ1=jω(a1+a3)exp(jωt);

(8)

υ2=-jω[a1cos(kl)+a2sin(kl)+a3cosh(λl)+a4sinh(λl)]exp(jωt);

(9)

M1=EI(-a1k2+a3λ2)exp(jωt)=0;

(10)

M2=EI[-a1k2cos(kl)-a2k2sin(kl)+a3λ2cosh(λl)+a4λ2sinh(λl)]exp(jωt)=0.

(11)

将式(10)代入式(8)可得:

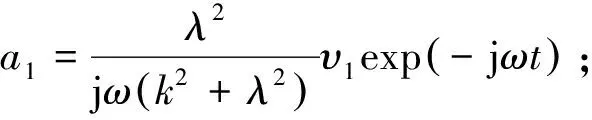
(12)

(13)

将式(12)和式(13)代入式(9)和式(11)可得:

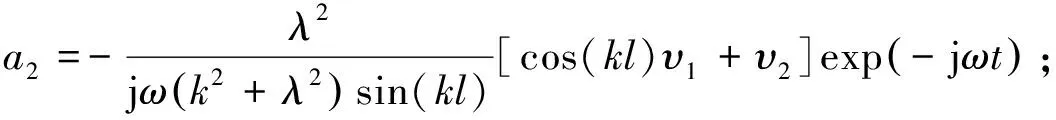
(14)

(15)

将a1,a2,a3和a4这4个待定常数代入杆两端的横向力表达式(7),整理得杆的两端力与质点横向振动速度的关系式为:

F1=EI(-a2k3+a4λ3)exp(jωt)=

(16)

F2=EI[a1k3sin(kl)-a2k3cos(kl)+a3λ3sinh(λl)+a4λ3cosh(λl)]exp(jωt)=

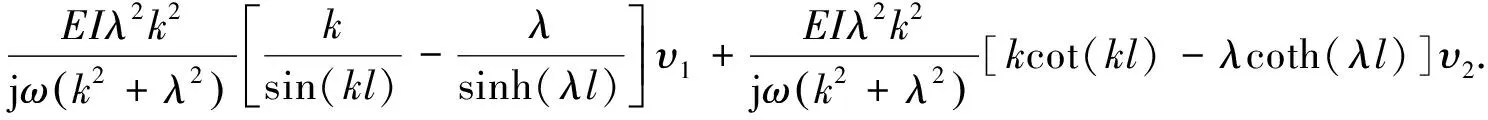
(17)

式(16)和式(17)可以进一步写成如下形式:

F1=z1υ1+z2υ2;

(18)

F2=z2υ1+z1υ2.

(19)

式(18)和式(19)中,z1和z2为均匀弹性杆的横向弯曲振动机械阻抗,其表达式分别为:

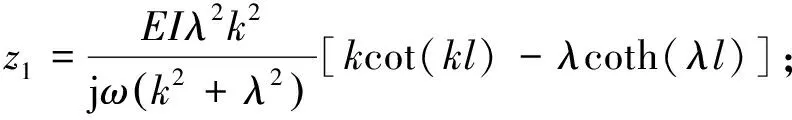
(20)

(21)

依据双端口等效网络理论,由式(18)和式(19)可得均匀弹性杆弯曲振动的T型等效电路如图2所示.

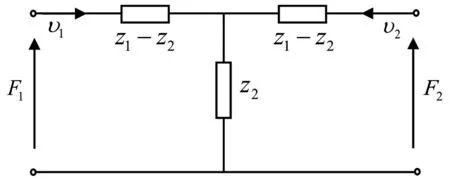
图2 均匀弹性杆弯曲振动的机电等效电路

2.2 Euler-Bernoulli弹性梁

式(1)中,若忽略剪切变形对弯曲振动的影响,则得均匀弹性杆在无激励条件下的动力学方程为

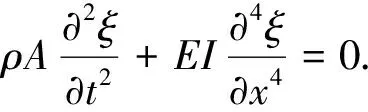
(22)

由式(22)可得杆的横向振动位移分布函数为

ξ(x,t)=[a1cos(kx)+a2sin(kx)+a3cosh(kx)+a4sinh(kx)]exp(jωt).

(23)

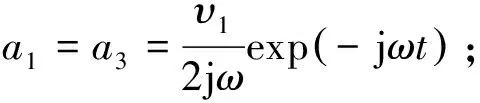
(24)

(25)

(26)

将a1,a2,a3和a4这4个待定常数代入杆两端的横向力可得:

F1=EIk3(-a2+a4)exp(jωt)=

(27)

F2=EIk3[a1sin(kx)-a2cos(kx)+a3sinh(kx)+a4cosh(kx)]exp(jωt)=

(28)

由式(27)和式(28)可知,杆两端的横向力F与振速υ同样满足式(18)和式(19)的互易关系,故振子的弯曲振动等效电路与图2相同,其机械阻抗z1和z2的表达式分别为:

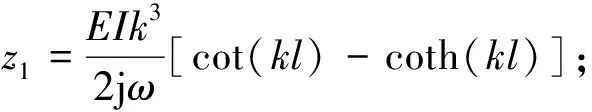
(29)

(30)

由等效电路图2可得两端自由均匀弹性杆的弯曲振动输入机电阻抗表达式为

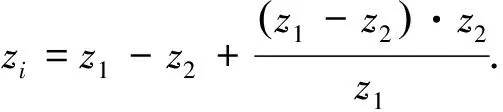
(31)

两端为自由边界情况下,均匀弹性杆弯曲振动的共振频率方程为

Im[zi]=0.

(32)

共振频率方程反映了振子弯曲振动的共振频率与其几何尺寸、材料参数和截面形状之间的相互依赖关系.当均匀弹性杆的几何尺寸、材料参数和截面形状确定后,可通过频率方程求出振子的各阶弯曲振动共振频率,或者给定频率,求出相应的几何尺寸.

3 有限元仿真

为验证上述等效电路模型的正确性,利用Comsol有限元软件计算分析了不同几何尺寸杆的弯曲振动共振频率.选取振子的材料为钢,材料特性参数为:密度ρ=7 850 kg/m3;泊松比σ=0.28;弹性模量E=2.05×1011Pa.通过计算分析长度l=200 mm、宽度w=20 mm、高度h=10 mm的两端自由矩形截面均匀弹性杆的弯曲振动共振频率,得到其各阶次弯曲共振模态的振型图和共振频率值,图3分别为其第1和第6阶弯曲共振模态振型图.

(a)第1阶弯曲共振振型 (b)第6阶弯曲共振振型

图3(a)和图3(b)分别为有限元计算得到的矩形截面均匀弹性杆第1阶和第6阶弯曲共振模态振型图.由图3可以看出,杆在弯曲共振模态下有较均匀的横向位移振幅;弯曲振动位移节点数(m)与阶次(n)满足n-m=1的关系,在实际工程应用中,振动位移节点通常作为系统固定或支撑位置.

利用等效电路法和有限元法分别计算分析了上述算例的前10阶弯曲振动共振频率,理论与仿真计算结果如表1所示.表1中:fE,fS和fC分别为利用Euler-Bernoulli梁等效电路法、Shear梁等效电路法和有限元数值计算得到的弯曲振动共振频率;Δ1=|fE-fC|/fC和Δ2=|fS-fC|/fC分别为2种梁弯曲共振频率的理论与仿真结果之间的相对误差.由表1可以看出,杆的弯曲振动共振频率及其相对误差随其振动阶次的增加而增大;Euler-Bernoulli梁共振频率的理论与仿真误差随振动阶次升高而快速增大;但Shear梁共振频率的理论与仿真误差较小,且在较大的弯曲振动阶次范围内吻合较好.

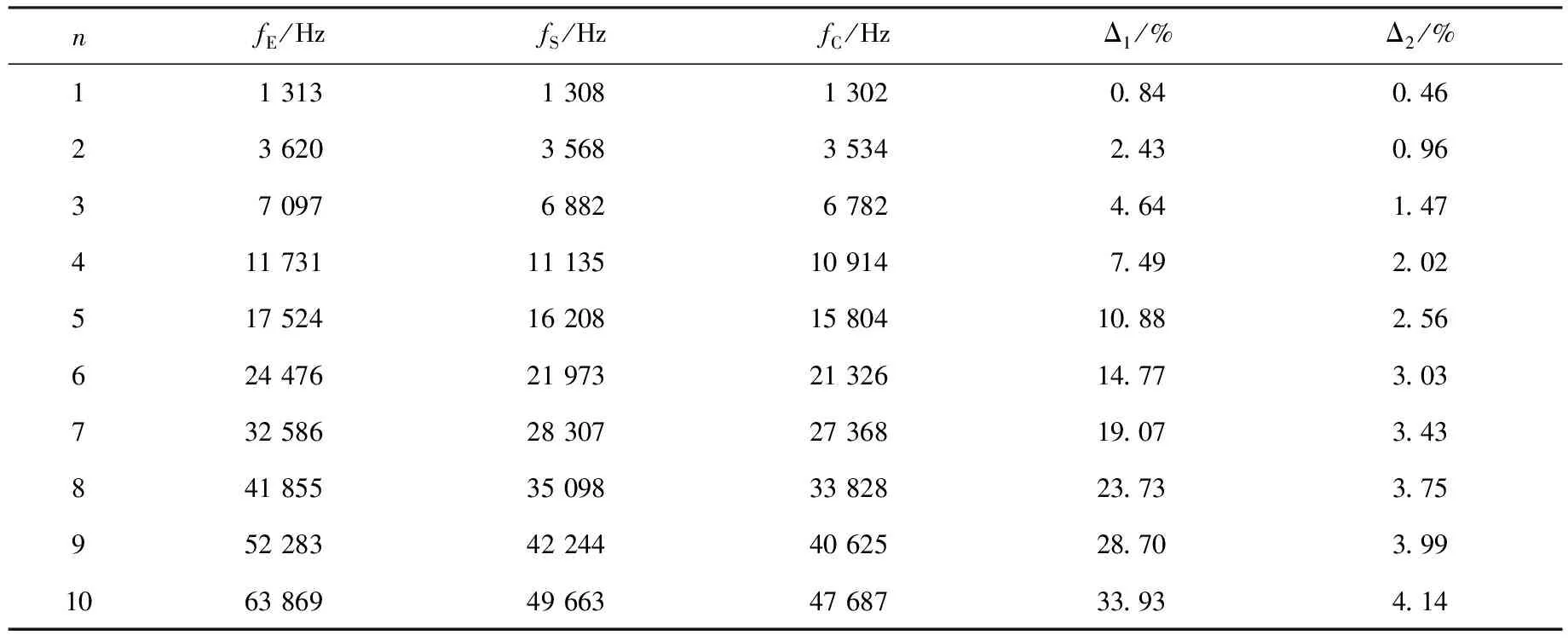
表1 矩形截面均匀弹性杆的各阶弯曲共振频率

选取长l=300 mm、宽w=20 mm的矩形截面均匀弹性杆为算例,探讨了杆的各阶弯曲振动共振频率与高度之间的关系,以长高比K=l/h表示矩形截面均匀弹性杆的不同几何尺寸.理论与仿真计算结果见图4.

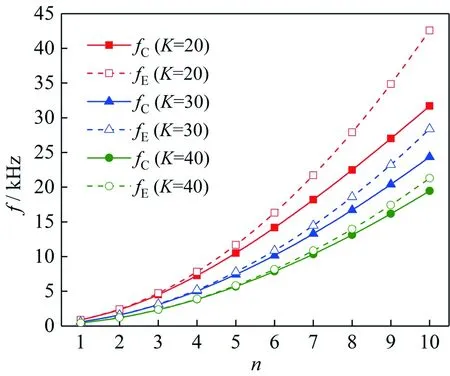
(a)Euler-Bernoulli梁理论计算值和仿真值 (b)Shear梁理论计算值和仿真值

选取高度h=10 mm、宽度w=20 mm的矩形截面均匀弹性杆为算例,探讨了杆的各阶弯曲振动共振频率与长度之间的关系,理论与仿真计算结果如图5所示.

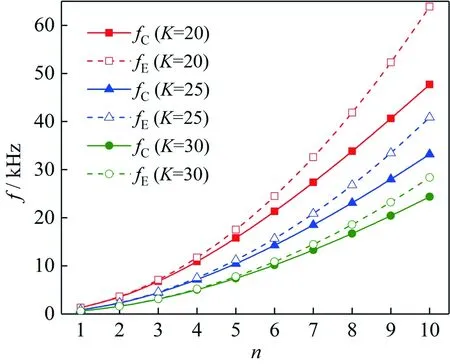
(a)Euler-Bernoulli梁理论计算值和仿真值 (b)Shear梁理论计算值和仿真值

由图4和图5可知,2种梁理论计算的均匀弹性杆弯曲共振频率值的误差随其振动阶次的增加而增大,随其长高比的增加而减小;Euler-Bernoulli梁理论等效电路法适用于计算振动阶次较低和长高比较大的杆弯曲振动共振频率;Shear梁理论等效电路法计算的杆弯曲共振频率与有限元法的计算结果吻合较好.

误差主要来源:一方面是杆的弯曲振动并非理想的一维波动,而是复杂的三维弹性动力学问题;另一方面随着杆的弯曲,共振频率的升高,三维弹性动力学的转动惯性、剪切变形的影响更加显著;此外,Euler-Bernoulli梁理论因忽略了截面转动惯性和剪切变形,故适用于求解弯曲振动阶次较低和长高比较大的动力学问题;Shear梁理论考虑了剪切变形,可大幅提高计算杆弯曲振动的尺寸范围和振动阶次.

4 结 论

基于Shear梁和Euler-Bernoulli梁理论的均匀弹性杆动力学方程与机电类比原理,推导了其机电类比等效电路及共振频率方程;探讨了矩形截面均匀弹性杆的前10阶弯曲振动的共振频率与其长度和高度之间的依赖关系,并进行了有限元仿真计算和验证,研究结果表明:

1)均匀弹性杆弯曲振动的等效电路与传统杆形超声振子的纵向和扭转振动类似,可用互易T型等效电路来描述.

2)通过等效电路法计算得到杆的弯曲共振频率理论与数值仿真结果误差随其弯曲振动阶次的升高而增大,而随其长高比的增加而减小.

3)Euler-Bernoulli梁理论等效电路适用于计算振动阶次较低和长高比较大的杆弯曲振动共振频率,Shear梁理论可大幅提高计算杆的尺寸范围及弯曲振动阶次.

值得指出的是,本文研究的均匀弹性杆弯曲振动等效电路较现有的解析理论及矩阵传递法,其物理意义更明确、求解更简便,从而为分析和处理杆形振子的弯曲振动问题,特别是由杆形振子组成复合振动系统的纵弯和扭弯等耦合振动提供了一种等效电路分析方法.