受媒体报道和治疗影响的传染病模型的最优控制分析
2023-11-09刘中凯刘俊利刘白茹
刘中凯, 刘俊利, 刘白茹
(西安工程大学 理学院,陕西 西安 710048)
传染病的每次大规模流行都会造成人口减少,经济下滑,而面对传染病的重大危害,如何采取有效措施快速控制传染病的进一步扩散并使得经济成本最低,成为了学者们研究的重要课题.
文献[1-2]建立了一个疟疾传染病模型,利用最优控制理论得到了使疾病灭绝的最佳条件,而当疾病无法灭绝时,利用庞特里亚金最大值原理得到了控制疾病的最优条件.文献[3]建立了一个结核病模型,并考虑到二次感染的情况,通过分析得到了最优控制策略,极大地降低了疾病的控制成本,并有效减少了感染者和潜伏者的数量.文献[4]研究了结核病与艾滋病联合感染传播的传染病模型,分析了各种组合策略对疾病传播的影响,并利用增量成本效益比分析所有控制措施的成本效益,最终得到了控制疾病传播的最优策略.文献[5]以喀麦隆发生的结核病为例,建立了一个具有控制措施的传染病模型,找到了控制结核病的最佳方法.结果表明,通过多种控制措施相结合的方法控制结核病,可以大幅降低经济负担,并有效遏制结核病的扩散.文献[6]建立了一个关于控制疟疾传播的数学模型,通过理论分析和数值模拟发现,当蚊帐使用率约为10%以及约50%的感染者得到有效治疗时,对疟疾的控制效果最好,控制成本最低.文献[7]提出了一个带有疫苗接种和治疗的传染病模型,为了使传染病的控制成本最低,利用最优控制理论研究了时变控制措施的情况,得到了最优控制策略.文献[8]考虑了一个受媒体报道宣传影响的SEI传染病模型,并利用最优控制理论进行分析,得到了使目标函数值最小的最优条件,通过数值模拟直观表现了控制措施对疾病扩散的抑制作用.文献[9]建立了一个SIRS传染病模型,研究了降低传染率和提高恢复率两种最优控制措施对疾病扩散的影响,并利用最优控制理论得到了有效控制疾病传播且成本最低的方法,研究表明,采取治疗等有效措施后,疾病逐渐被控制并最终消亡.文献[10]考虑了具有媒体报道和潜伏期时滞的传染病模型,对模型进行了最优化理论分析,得到了使感染者人数最少且媒体宣传费用最低的最优控制策略.文献[11]研究了具有疫苗接种、媒体报道和治疗3种控制措施的传染病模型,对3种控制措施进行了最优化分析,得到了抑制麻疹传播的最优控制策略,结果表明,在抑制麻疹传播方面,媒体的宣传报道和疫苗接种比治疗措施更加有效.
媒体的宣传对控制传染病具有重要作用,媒体报道提高了人群的防控意识,使其行为发生改变,近而阻碍疾病传播. 而对感染者进行相关治疗也是控制传染病的有效手段,所以本文在文献[10-11]的基础上将易感者分为无意识易感者和有意识易感者,并考虑到治疗者会被二次感染的情况,建立具有媒体报道和治疗措施的传染病模型.为了降低媒体报道和治疗的成本以及感染者数量,建立了最优控制系统,并利用最优化理论对系统进行分析,得到了使感染者数量最少且经济成本最低的最优控制措施.
1 模型的建立
根据仓室模型的建模思想,将总人口共分为5个仓室:无意识易感者Sn(t),有意识易感者Sa(t),感染者I(t),接受治疗的患者T(t)以及媒体报道信息量M(t).设人口总数为N(t),则N(t)=Sn(t)+Sa(t)+I(t)+T(t).设人口的输入率为A,人口自然死亡率为d,因病死亡率为a,β0和β1分别表示染病者对无意识易感者和有意识易感者的传染率,β2表示染病者对接受治疗的患者的传染率, 根据生物学意义,假设β0>β1,β0>β2.λ表示易感者从无意识到有意识的转化率,λ0表示意识的丧失率,θ表示感染者的治愈率,μ表示媒体项目的贯彻率,μ0表示媒体宣传过程中信息的耗损率.依据以上假设,建立如下模型:
(1)
系统(1)的初始条件为
Sn(0)≥0,Sa(0)≥0,
I(0)>0,T(0)≥0,M(0)≥0.
(2)
假设以上所有参数都是正常数.
下面将研究系统(1)在初始条件(2)下解的非负性和有界性,记
由定理1可知Γ为系统(1)的正向不变集.
定理1系统(1)在条件(2)下的解(Sn(t),Sa(t),I(t),T(t),M(t))始终是非负有界的.
证明首先,易证解的非负性.下面证明解的有界性.
总人口N(t)满足下列微分方程
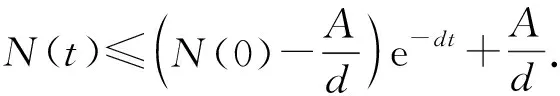
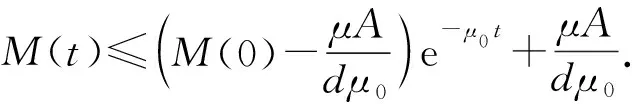
2 基本再生数和无病平衡点的稳定性分析
其中Q=θ+d+a.

证明系统(1)在无病平衡点E0处的特征方程为
(Z+d)(Z+μ0)(Z+λ0+d)(Z+a+d)×
(3)
显然,方程(3)有4个负根:Z1=-d,Z2=-μ0,Z3=-λ0-d,Z4=-a-d.而Z5=(R0-1)Q,则当R0<1时,Z5<0,无病平衡点E0是局部渐近稳定的;当R0>1时,Z5>0,无病平衡点E0是不稳定的. 定理2得证.
定理3当R0≤1时,系统(1)的无病平衡点E0在Γ内是全局渐近稳定的.
证明构造Lyapunov函数L=I,则L沿系统(1)轨线的全导数为
β0I(Sn+Sa+T)-(θ+d+a)I≤
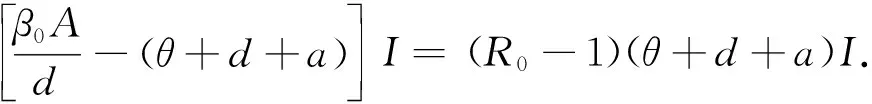
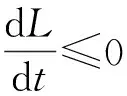
3 地方病平衡点的局部稳定性和疾病的持久性
解得
(5)
其中
X1=λμβ2(a+d)>0,X2=λμ(a+d)>0,
X3=β1β2(μ0β0+λμ)>0,
X4=μ0β0β2(λ0+d)+β1(a+d)(μ0β0+λμ)>0,
X5=μ0β0(λ0+d)(a+d)>0.
由(5)式和系统(4)可得关于I*的方程:
I*3+pI*2+qI*+r=0,
其中
p=
定义h(I*)=I*3+pI*2+qI*+r.
结合定理3可得下列结论.
定理4(ⅰ) 当R0≤1时,系统(1)不存在正平衡点.
(ⅱ)当R0>1时,系统(1)至少存在一个正平衡点.
定理5当R0>1且β1≥β2时,系统(1)的正平衡点E*是局部渐近稳定的.

H1=λM*+β0I*+d,
H2=λM*(β1I*+d)+(β0I*+d)(β1I*+λ0+d),
dβ0β1β2I*2(β1I*-β2I*)+
显然,H1>0,H2>0,H3>0.又因为β0≥β1≥β2,所以H4>0,H5>0,因此矩阵JE*为负定矩阵,即矩阵JE*的特征值都具有负实部.从而当R0>1时,地方病平点E*是局部渐近稳定的. 定理5得证.
β1和β2分别表示染病者对有意识易感者和接受治疗的患者的传染率,患者接受相关治疗后可以获得一定程度的免疫.因此,患者二次感染的概率应该低于第一次感染的概率,所以假设β1≥β2是合理的.
根据文献[13-14]中的证明方法可以得到疾病的持久性.

4 最优控制模型
考虑到媒体报道的过程以及对感染者进行治疗的过程都需要高额的费用,为了使防控成本最低且被感染的人数最少,用最优控制函数μ1(t)代替意识转化率λ,用最优控制函数μ2(t)代替治疗率θ进行最优控制理论分析.
首先,考虑总成本函数:
J[μ1(·),μ2(·)]=
(6)
控制系统为
系统(7)的初始条件与系统(1)的初始条件相同. (6)式中tf为控制措施的结束时间,各部分含义如下:
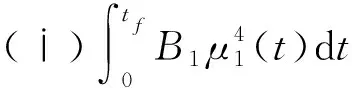

最优控制问题的拉格朗日函数为
(8)
控制变量μ1(t)和μ2(t)满足控制集:
Uad={(μ1,μ2)∈L(0,tf)|0≤μi(t)≤1,i=1,2}
.
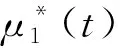
下面在时间区间[0,tf]内对控制最优解μi(i=1,2)进行分析.
系统(7)存在伴随变量λi=(λ1,λ2,λ3,λ4,λ5),则哈密尔顿函数为
H(Sn,Sa,I,T,M,μ1,μ2,λi)=
λ1(A-μ1(t)MSn-β0SnI+λ0Sa-dSn)+
λ2(μ1(t)MSn-β1SaI-λ0Sa-dSa)+
λ3(β0SnI+β1SaI+β2TI-μ2(t)I-aI-dI)+
λ4(μ2(t)I-β2TI-aT-dT)+λ5(μI-μ0M).
进而得到如下系统:
(9)
系统(9)满足横截性条件:λi(tf)=0,i=1,2,3,4,5.根据控制条件和哈密尔顿函数可得
解得
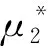

为了进一步反映最优控制函数μ1(t)和μ2(t)对疾病传播的控制效果,下面根据实际意义进行数值模拟.
5 数值模拟
本节将对最优控制函数μ1(t)和μ2(t)进行数值模拟. 首先,设定参数值如下:
A=2,β0=0.006,λ0=0.005,
d=1/78,β1=0.003,a=0.1,β2=0.002 5,
μ=0.3,μ0=0.1,μ1max=0.9,μ2max=0.9,
B1=5 000,B2=1 000.
(10)
在参数(10)下,取初值(100,10,8,3,1),考虑同时采取两种控制措施与不采取任何控制措施的情况下,染病者数量的变化(图1a). 当媒体报道和治疗两种控制措施同时实施时,控制措施函数μ1(t)和μ2(t)随时间的变化情况见图1b.
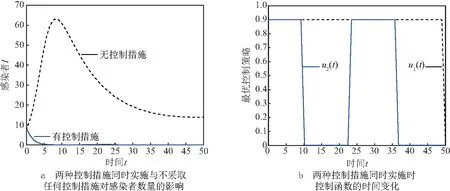
图1 初值为(100,10,8,3,1)时,控制效果对比图及控制措施函数的时间变化图
由图1a可以看出,当疾病出现时,如果不采取控制措施,疾病将暴发并流行,而当采取媒体报道和治疗两种控制措施时,可以有效减少感染者数量,抑制疾病传播,并使疾病最终消亡. 由图1b可以看出,μ1(t)以最大值对疾病进行持续性控制,而μ2(t)以最大值对疾病进行间歇性控制.这说明媒体的持续报道在传染病的控制过程中具有重要作用,但仅通过媒体报道改变人们的行为并不能达到最优效果,只有采取媒体报道与治疗相结合的方法,才能达到控制疾病传播的最优效果.
在参数(10)下,取初值(32,2,12,0,2),比较仅采取媒体报道控制措施与不采取任何控制措施对染病者数量的影响,研究控制函数μ1(t)随时间的变化情况(图2).由图2a可以看出,媒体报道可以有效降低感染者数量,抑制疾病传播,但并不能使疾病消亡.由图2b可以看出,μ1(t)始终以最大值对疾病进行控制,说明当人群中出现感染者时,为了防止人们的防控意识松懈,使人们在传染病流行期间始终保持正确的防控行为,减少不必要的接触,达到控制传染病的最优效果,媒体必须持续不间断地对传染病进行报道.

图2 初值为(32,2,12,0,2)时,控制效果对比图及控制措施函数的时间变化图
在参数(10)下,取初值(100,0,40,30,0),将只采取治疗的控制措施与不采取任何控制措施对感染者数量的影响进行对比,结果见图3a.控制措施函数μ2(t)随时间的变化情况见图3b.由图3a可以看出,治疗可以有效降低感染者数量,抑制疾病传播. 由图3b可以看出,μ2(t)以最大值对传染病进行间歇性控制.当μ2(t)以最大值对传染病进行控制时,可使感染者数量迅速降低,控制效果明显.而当μ2(t)停止对传染病进行控制时,感染者的数量又迅速增加,说明当传染病流行时,若只采取治疗的控制措施,尽管可以使用控制成本最低的最优控制策略,但使成本最低的同时并不能使传染病消亡或者趋于稳定.若为了控制经济成本而停止采取控制措施,则存在传染病二次暴发的可能性.

图3 初值为(100,0,40,30,0)时,控制效果对比图及控制措施函数的时间变化图
综上,当传染病出现时,如果不采取任何控制措施,传染病将会暴发并流行,而采取一定控制措施能够有效抑制传染病的流行暴发,甚至使其消亡.而在对传染病的控制效果上,采取多种防控措施相结合的方法比采取单一控制措施的效果更加明显.
6 结论
文章首先建立了一个受媒体报道和治疗共同影响的传染病模型,证明了模型解的非负性和有界性. 计算得到了模型的基本再生数和无病平衡点,并且证明了无病平衡点的局部稳定性和全局稳定性.分析了地方病平衡点的存在性和局部稳定性,并给出了疾病持久性的定理.为了使感染者数量最低且控制疾病传播扩散的费用最少,以媒体报道和治疗作为两种控制措施,建立了最优控制模型,并利用庞特里亚金最大值原理得到了最优控制策略.最后根据实际情况进行了数值模拟.研究发现,当传染病出现时,通过媒体报道可以提高人群的防控意识,使其行为发生改变,进而对疾病的传播起到一定的抑制作用;通过对感染者进行治疗,也可以有效降低感染者数量,但同时采取媒体报道和治疗两种措施对疾病流行的抑制效果最为明显.因此,当疾病暴发时,只采取单一的控制措施是远远不够的,应该采取多种控制措施相结合的策略,进行全方位控制,以谋求防控成本最低、传染病危害最小.
附录:
