面向复杂地质构造煤田的地震勘探关键技术

杨广宪

（中国煤炭地质总局地球物理勘探研究院，河北涿州 072750）

0 引言

随着煤炭资源枯竭，煤矿开采普遍进入地质构造复杂区及深部开采区，褶皱、断裂及小尺度地质体异常发育，矿区采掘工作面穿越地质构造带成为常态，给矿井工作面掘进及回采带来许多不利因素［1］，矿井生产安全、经济效益面临挑战，期望获得高精度的地质勘探成果，对地震勘探技术提出了更高的要求。在实际工作中，通过深入研究、试验对比，形成了以全方位地震采集，层析精校正、叠前偏移、时频分解、属性反演等为代表的一套完整高精度地震勘探技术体系，即全方位三维地震采集技术，高精度三维地震成像技术，精细地震解释技术［2-3］。在几个复杂地质构造勘探区应用中，极大提高了地震勘探的成果精度，满足了煤炭开采、开发的地质需要。

1 全方位三维地震采集技术

相比早期常规窄方位观测系统，全方位三维地震采集具有360°空间连续滚动观测的特点，各属性样点在三维空间域分布均匀，纵横比接近1∶1，有均匀的炮检距和方位角分布，纵横向都能获得均等的地震波场信息，能够突出各方向有效信息［4］。全方位连续滚动能够最大限度减小采集脚印，从而减小观测系统噪音，获得高保真地震信号［5］。具备均匀炮检距、方位角和覆盖次数的地震数据，通过“三高”地震资料处理，可以真实、完整的揭示地质构造的空间形态，能够最大能力提取有效地质信息和属性参数。

某煤田早期进行过地震勘探，采用束状窄方位观测系统采集，纵横比小于0.5，图1a 为其观测系统波场图，激发和接收形成的波场方位单一、狭窄，地质构造的呈现存在局部性。从图1c地震剖面可知：煤系地层与上覆地层呈角度不整合接触，几条大断层切割煤层，小断层、褶曲极其发育，但成像存在局部模糊现象，多解性严重，无法真实、高精度呈现地质体的面貌，地质构造空间展布比较粗糙，解释误差较大［6］；为解决测区复杂的地质构造问题，后期采用全方位观测系统重新采集，在各个方位上均匀分布炮检距，纵横比为1∶1，图1b 所示：波场在整个空间传播，呈现一个球形等时面，对地质构造的呈现具有全面性。从图1d地震剖面可知：早期成像模糊的区域，变得清晰准确，小断层分布更精细，地质构造的属性更加准确，刻画地质构造的能力显著提高，取得了丰富的高精度地质成果。可见全方位观测系统采集的优势，使地震成果精度远高于窄方位观测系统，是高精度地震勘探的关键技术。

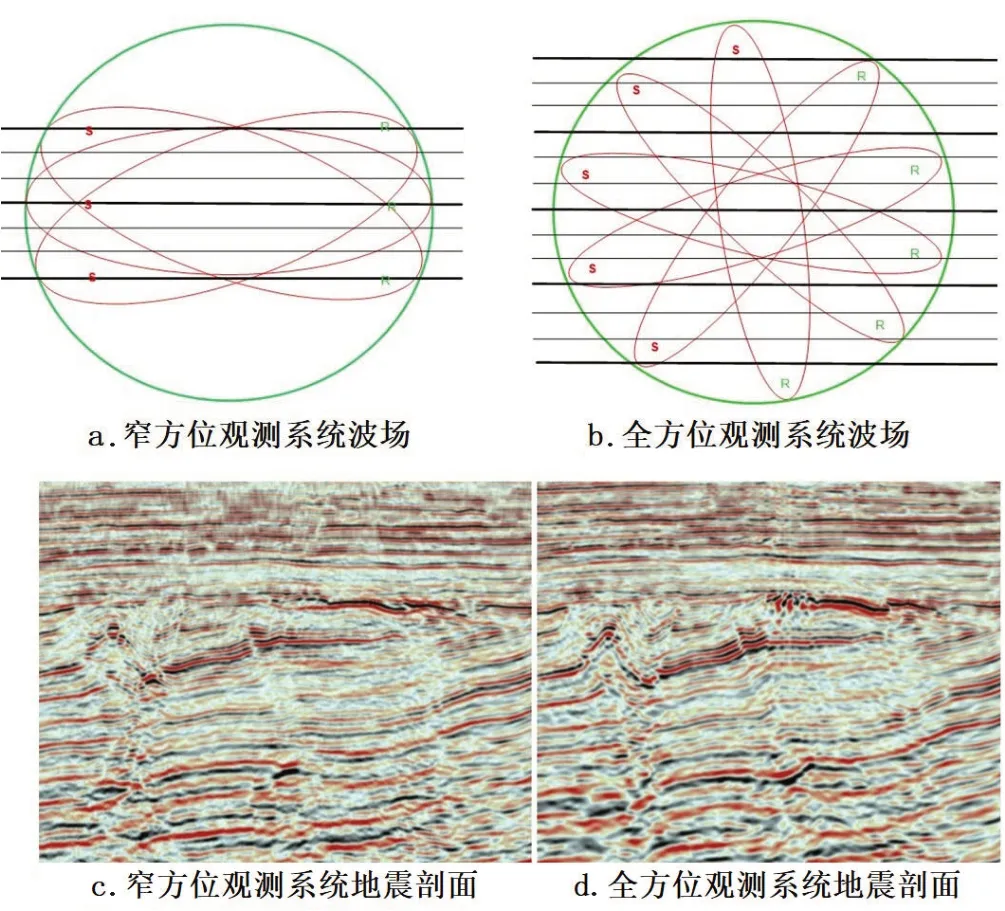
图1 窄方位与全方位观测系统地震剖面对比Figure 1 Comparison of seismic sections between narrow azimuth and omnidirectional observation systems

2 高精度三维地震成像技术

高信噪比、高保真度、高分辨率的“三高”地震资料处理技术，是地震勘探反射波成像的重要手段，包含的内容很多，本文只简单阐述三个影响高精度地震成像的关键技术。

（1）层析静校正技术

在某些地区，静校正工作一方面已经成为衡量资料处理技术水平高低的重要标准，另一方面又成为提高资料处理质量的瓶颈［7］。层析静校正技术是目前较先进的方法，其原理是对地下介质进行网格化，并假设每个网格单元内是均匀的，通过射线反演，计算介质模型。把网格划分足够小，且保证观测密度足够大，就能够准确求取网格单元介质模型，进而获得整个勘探区的近地表模型，即可以解决短波长静校正问题，也能够解决长波长静校正问题，满足了复杂地区高精度勘探需求［8］。

初至波旅行时间与近地表模型之间的关系：

对式（1）离散化成矩阵方式，通过对代数方程组（2）求解，获取近地表模型

式（1）、（2）中：t为地震信号旅行时间；s(x，y，z)为模型单元介质慢度函数；dl为地震波旅行距离的微分；T为地震信号旅行时间矩阵；A为地震波旅行距离矩阵；S为单元网格慢度矩阵。

早期的静校正方法为折射静校正技术，图2a 为某山前地带煤田折射法求取的近地表模型，结果为简单的层理结构，地层间存在准确速度界面，是典型的理论性模型，与测区近地表模型是不符的。图3a是测区原始地震记录，图3b是折射法静校正后的地震记录，可见静校正效果一般，虽单炮记录地表一致性明显改善，但静校正误差较大。

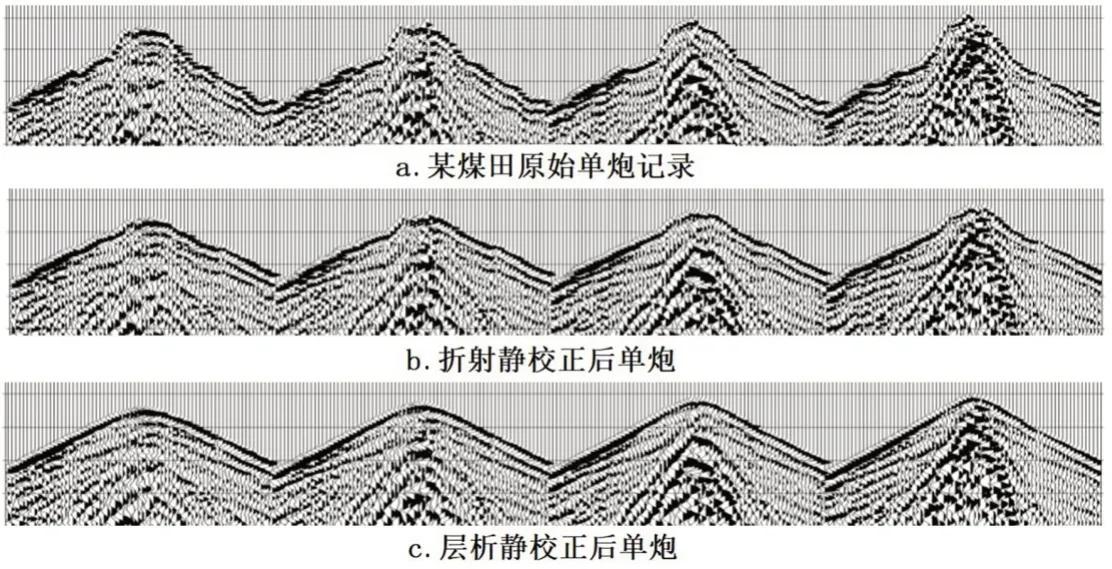
图3 折射法与层析法静校正后单炮对比Figure 3 Single shot comparison between refraction method and tomography method after static correction

随着技术的发展，当前较好的静校正方法为层析静校正技术，为提高测区的勘探精度，对该煤田原有地震勘探数据进行了二次处理工作，主要是应用层析静校正技术。图2b 为层析法求取的近地表模型，可见介质间不存在明确的速度界面，体现了介质在整个空间的渐变分布，山前地带特征明显，与现实中的近地表介质模型状态是一致的。图3c 是层析法静校正后的单炮记录，与图3b相比，静校正精度大幅提高，效果差异明显，说明层析静校正技术是复杂勘探区高精度成像的关键技术。

（2）保真去噪技术

地震勘探的各种干扰信号中，严重影响“三高”成像精度的是规则噪声，尤其那些呈现一定的双曲特征，频带与有效波频带重合，能量较强的干扰信号，影响最为严重且去除难度较大。锥形滤波去噪技术是一种基于十字排列域噪声衰减方法：在频率波数域设计滤波器，三维锥形滤波器以其形态为锥形而得名［9］。

三维锥形器滤波器的设计原理是：对三维原始叠前地震数据体，沿检波线、炮线方向排序抽取数据，经傅里叶变换到频率、波数域，依据实际资料的频率、速度范围等参数设计锥形滤波器。设三维地震记录的原始信号为p(x，y，t)，滤波因子为h(x，y，t)，有效地震反射信号为q(x，y，t)，三者在时空域中满足以下褶积关系：

对式（3）进行傅里叶变换，得到频率、波数域有效信号、原始信号、滤波因子的相乘关系：

式（3）、（4）中：x、y为纵横向炮检距；t为地震信号旅行时间；kx、ky为纵横向视波数；ω为地震信号角频率。

设计三维锥形滤波器，主要根据不同地区面波、地滚波传播速度与有效波传播速度的差异，多采用速度带通或速度带陷两种方式，应用频率波数域锥形滤波方程（4）去除以地滚波、面波为主的规则噪声［10］。图4 是正演模型的单炮记录，混入了一定速度的规则噪声，应用锥形滤波后，噪声几乎被去除干净，而有效信号没有受到影响。

图4 正演模型应用锥形滤波器Figure 4 Conic filter applied to the forward modeling model

图5是某煤田地震勘探单炮记录，含有面波、地滚波等强能量规则噪声，有效波能量相对微弱，信噪比小于1.0，煤层反射波无法成像，属于复杂勘探地区，消除这组规则噪声，改善信噪比，是成败的关键。通过锥形滤波后，噪声几乎全部消除，有效波完全保留，能量明显改善，信噪比大于2.0，保真去噪的目标得以实现，显著提高了煤层反射波成像的信噪比和保真度，锥形滤波去噪技术是“三高”处理的关键技术。

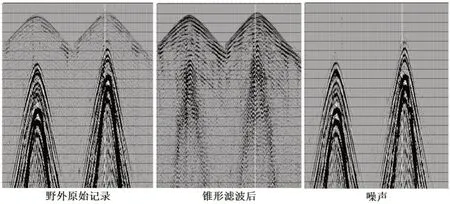
图5 地震资料应用锥形滤波去噪Figure 5 Denoising of seismic data by cone filter

（3）叠前偏移技术

Kirchhoff 积分法是叠前时间偏移的主要方法，既可使速度分析和偏移成像同时进行，又可通过偏移速度分析，对速度模型不断修改，保障叠前时间偏移成像效果，成像质量主要依赖于速度模型的准确性［11］。首先，应用速度分析或老成果的解释速度建立初始速度模型，运行叠前时间偏移并输出CRP道集。然后，应用百分比扫描和剩余速度分析技术，修正初始模型，进一步提高速度模型的精度。通过几次迭代，使速度模型趋于真实，获得最佳偏移成像，高精度呈现复杂微小的地质构造。

叠前时间偏移处理需要在浮动基准面上进行，偏移后再校正到最终基准面上。图6 中S和R分别表示震源和检波点，Ds和Dr分别为震源和检波点与共中心点的垂直距离，ts0和tr0分别为震源和检波点自激自收反射时间，tsc和trc分别是震源和检波点移动到最终基准面的校正量。偏移后的CRP 道集处于浮动基准面上，也可以输出到最终基准面上，用于后续如AVO等反演工作［12］。

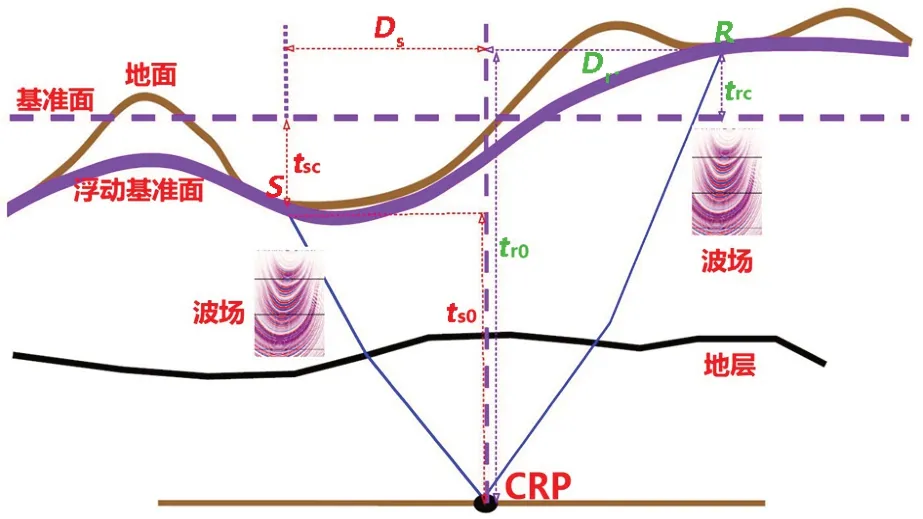
图6 叠前时间偏移原理图Figure 6 Schematic diagram of prestack time migration

叠前时间偏移技术在二次处理工作中，广泛应用，效果显著。图7a为早期叠后偏移的时间剖面和顺层切片，可知测区地处几条大断裂之间，地层呈不同倾角褶曲赋存，产状复杂，空间变化大；存在不同规模的断层，尤其小断层特别发育，像一个破碎的盘子一样，地质构造极其复杂；局部成像模糊，存在多解性，解释精度一般。图7b 是二次处理后，应用了叠前时间偏移技术后的地震剖面及顺层切片，相比图7a，叠前时间偏移的地质构造成像更清晰、准确，小尺度地质构造刻画更加精准，取得高精度地质成果。说明叠前时间偏移在理论和方法上相比叠后时间偏移具有明显的优势，复杂地质构造的成像归位更准确，精度更高。

图7 某煤田叠后（a）与叠前（b）时间偏移对比Figure 7 Comparison of post-stack（a）and pre-stack（b）time migration in a coalfield

3 精细地震解释技术

频谱分解是精细解释的重要技术之一，是基于薄层调谐理论演化而来，其数学原理是离散傅里叶变换或最大熵变换，在短时窗内对地震道信号进行频谱分解。得到的相位谱用于描述地质体边缘的不连续性，呈现地震异常边界或地质构造边界。而得到的振幅谱能够描述储层厚度变化［13］。

小波变换是实现频谱分解的核心，将地震信号的时间-振幅域地震道变换到时间-频率域地震道。随着时窗宽窄、尺度等参数的变化，能够获取不同频率的时频地震道信息，对小尺度、隐伏性地质体的成像具有较强的能力。它能够同时改善地震信号时间分辨率和频率分辨率，对地质构造的空间差异性反映更加突出［14］。

假设地震信号为f(t)，其小波变换：

式中：WT(a，τ)为小波变换函数；a为尺度因子；τ为平移因子；ψ(t)为小波基函数；其傅里叶变换(ω)满足容许性条件，即。

据式（5）可知，随尺度因子a的变化，其窗口的大小和形状都在改变，从而适应不同频率的地震道，适应不同分辨率的要求［15］。围绕时窗设计和小波基函数的选择，小波变换演化出如连续小波变换、S-变换等多种频谱分解方法。不同类型时频分析技术，时频分辨率也有差异，具有各自的特点［16］。

频谱分解技术已广泛应用在二次解释工作中，图8a是某煤田原有常规成果数据体地震剖面及顺层切片，可见煤系地层与上覆地层呈角度不整合接触，赋存多组煤系地层，褶曲、断层发育，地质构造较复杂。但成像局部层理模糊、产状错乱，多解性严重，解释精度一般。图8b是应用频谱分解技术后，用于二次解释的成果数据体地震剖面及顺层切片。可见，地层成像更加丰富，层理关系更加清楚，断层刻画更加精细；在顺层切片图上，地质构造的空间展布更加清晰、准确，分辨率显著提高，获得了高精度地质成果，说明频谱分解技术是精细地震解释的关键技术。

4 结论

早期常规地震勘探的采集、处理、解释技术已无法满足资源勘探的要求，而广泛应用的全方位地震勘探采集、处理和解释技术，需要有针对性的关键技术联合完成。在实际工作中，应用几种地震勘探关键技术的成果表示，相比常规技术都具有较大的优势，能够满足高信噪比、高保真、高分辨率的地质要求，对高精度解决煤田复杂地质构造起到关键作用。