跨河桥交叉口协调控制策略研究——以济南市为例

张统洋,王 婷

(1.中国公路工程咨询集团有限公司,北京 100089;2.北京大唐高鸿数据网络技术有限公司,北京 100191)

1 引 言

受地表河流的影响,在城市路网中存在一种特殊的短连线交叉口——跨河桥交叉口,即跨河道路与两条沿河道路交叉所形成的两个平面交叉口,交叉口间距短,交通关联性强[1]。特别是在交通高峰时段,由于交叉口间容纳交通量不能满足下游车辆排队需求,排队溢出现象时有发生,不仅会导致交叉口死锁,甚至造成局部路网瘫痪,而且大量车辆怠速排队引起的碳排和能耗,也不符合城市绿色发展的理念。因此研究跨河桥交叉口的协调控制显得尤为重要。近年来,国内外对短连线交叉口排队溢出问题的研究渐臻成熟。杨晓光、付晶燕[2]对短连线交叉口进行界定,利用波动理论和车流运行时空图建立了短连线交叉口群的通行能力计算模型,同时注意到相位差会对通行能力产生影响,但未做深入研究;刘岩[3]假设关联交叉口间的相位差为0,以短连线信号交叉口车辆排队长度不大于路段长度为条件,提出了过饱和状态下短连线的延误模型;齐立群[4]将排队长度和相位差的研究相结合,基于波动理论提出饱和条件下动态调节短连线交叉口相位差的方法;杨晓芳、芮丽丽[5]针对短连线交叉口死锁问题,提出了基于车流无缝衔接的短连线交叉口协调控制模型,并以左转车流排队长度为约束,运用波动理论建立了排队约束模型;Liu H X[6]利用波动理论,对拥堵条件下信号控制交叉口的实时的排队长度做出了评价研究;吴先宇,李璐兵[7]基于美国NEMATS-2标准中提出的双环相位结构,针对信号合并和信号协调两类短连线交叉口分别建立两种控制方式对应的信号相位相序设置策略和信号配时方法。以往研究表明,调节相位差多被用作近距离交叉口的协调控制的主要手段,但是其首要目的是保证干线直行车流优先通行,忽视了交叉口左转车流对整个交叉口交通运行的影响。由于跨河桥交叉口间距过短,直行与左转、左转与左转间的车流冲突较普通交叉口更为严重,极易造成整个交叉口的拥堵甚至瘫痪,而鲜有研究对直行和左转车流的通行权分配进行分析探究。由此,以济南市为例,通过分析不同类型跨河桥交叉口的车流离散规律,兼顾直行和左转车流通行权的协调分配,从交叉口信号配时和空间优化设计角度提出相应的协调控制策略,并给出相位差的计算模型。

2 跨河桥交叉口拥堵成因分析

济南市共有4条大型河流及120条中小河流[8],部分河流流经城市内部,形成众多跨河桥交叉口。通过实地踏勘,依据交叉口车流离散规律将跨河桥交叉口归为3类(如表1所示),并发现:济南市城市内部跨河桥交叉口间距普遍小于规定值150 m[9],交通关联性强;为弱化关联交叉口间的相互干扰,在现行交通组织中多将次路(沿河道路)实施单向交通组织,同时压缩交叉口左转车流通行时间,以实现主路(跨河道路)直行车流快捷畅通的目的。但结果却未达到预期目标,拥堵时有发生,其拥堵成因如下。

表1 济南市跨河桥交叉口分类

(1)交通流冲突严重。虽然单向交通使整个交叉口组织简单化,但是直行与左转、左转与左转之间的车流冲突问题依旧严重,大大增加行车延误,车流冲突点如图1所示。

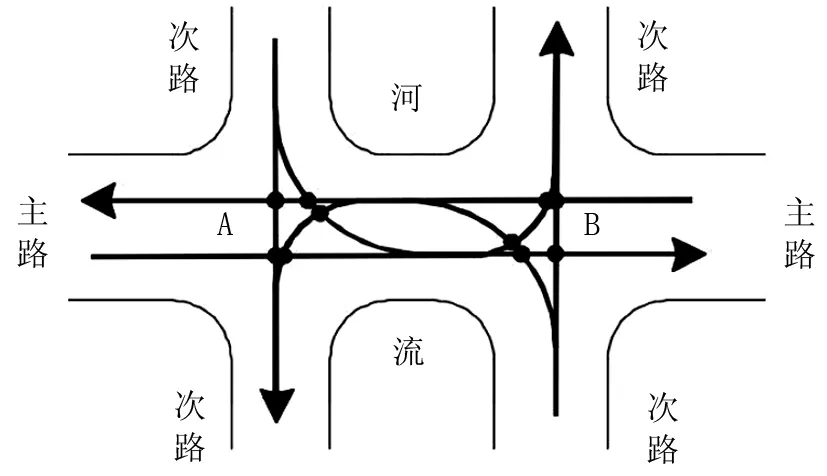
图1 跨河桥交叉口交通流冲突示意图

(2)交叉口间距过短。高峰时段,交叉口左转车流无法在有效绿灯时间内通过交叉口,车辆在交叉口间路段积压排队致使下游交叉口排队车辆经常蔓延至上游,阻碍上游交叉口车辆通行,形成死锁。

当交叉口间距小于交叉口最小间距时需要进行一体化设计[10],因此将跨河桥交叉口看成一个系统,基于车流离散规律,对相位和空间进行优化设计,消除较为严重的冲突点,减少交叉口间排队长度,协调控制各个方向交通流有序高效运行,提高系统通行能力。

3 跨河桥交叉口协调控制策略

3.1 非对称相位设计

Ⅰ型跨河桥交叉口主路采用干线协调控制,不产生排队。但次路左转流量较大,南北进口同时放行左转交通流存在冲突(如图2所示),车辆只能利用可穿越间隙通过交叉口,大大增加行车延误,倘若车辆在交叉口间路段滞留,极易造成交叉口死锁。因此,采用非对称相位设计,即次路各进口分别单独放行,主路各进口同时放行,相位设计如图3所示。

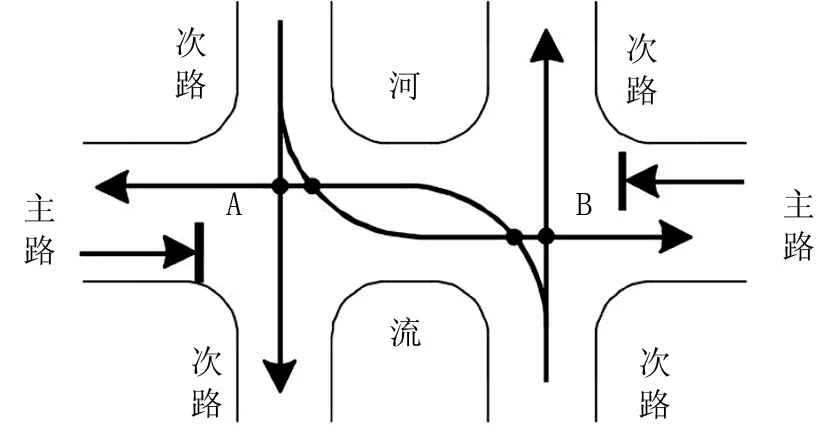
图2 左转车流冲突

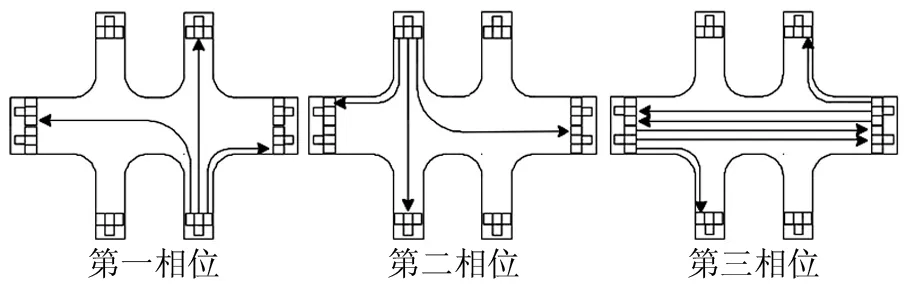
图3 非对称相位设计

假设第一相位为交叉口B南进口放行。当第一相位结束时,南进口与下游交叉口A东进口信号之间存在协调相位差θ,使车队最后一辆车顺畅驶出下游交叉口A,减少车辆滞留。

(1)

式中:L为交叉口间距,m;v为交叉口间的平均行驶速度,m/s。

第二相位与第三相位零相位衔接。交叉口A北进口左转车流可不停车驶出下游交叉口,而主路直行车流跟随左转车流通行实现无缝衔接,提高绿灯时间利用率。相位设计配时图如图4所示。

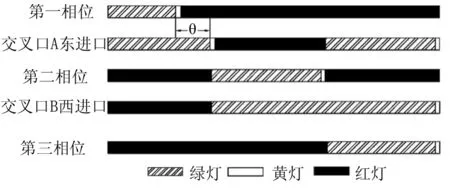
图4 非对称相位设计配时图

3.2 基于波动理论相位设计

针对Ⅱ型跨河桥交叉口间距可满足次路左转车辆排队需求的特点,牺牲左转车流的通行权,使其在交叉口间路段排队以消除左转车流间冲突点,如图5所示,相位设计方案如图6所示。

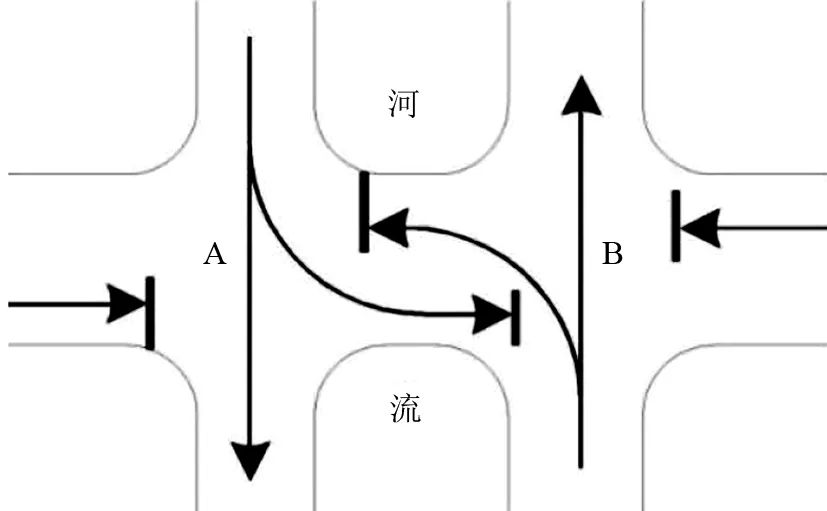
图5 左转车辆冲突消除

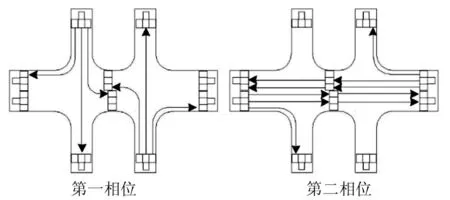
图6 基于波动理论相位设计示意图

同时,为确保排队不溢出,还需运用波动理论对相位差进行优化设计。以交叉口B为例,南进口放行时,直行、右转车流可直接驶出交叉口,左转车辆在交叉口间排队。当左转车流消散波传至交叉口B前,切换相位。因此整个过程的时间关系满足下式

w1(ta+ts)=w2ts

(2)

w1(ta+ts)≤L

(3)

ta=TAE=gBS

(4)

θ=ts

(5)

由以上各式推导可得

(6)

式中:θ为交叉口A东进口与交叉口B东进口与第二相位的相位差,s;ta为停车波波速,km/h;ts为启动波波速,km/h;w1为停车波传播时间,s;w2为启动波传播时间,s;L为交叉口间距,m;TAB为交叉口A东进口红灯时间,s;gBS为交叉口B南进口绿灯时间,s。

另外,为防止交叉口间路段有车辆滞留而产生额外延误,增加下游交叉口绿灯时间η清空滞留车辆,计算方法同公式(1)。

通过公式(6)可以看出,跨河桥交叉口协调相位差与波速和进口绿灯时间有关,并应根据车流到达率和车速进行实时动态调整。相位设计配时如图7所示。

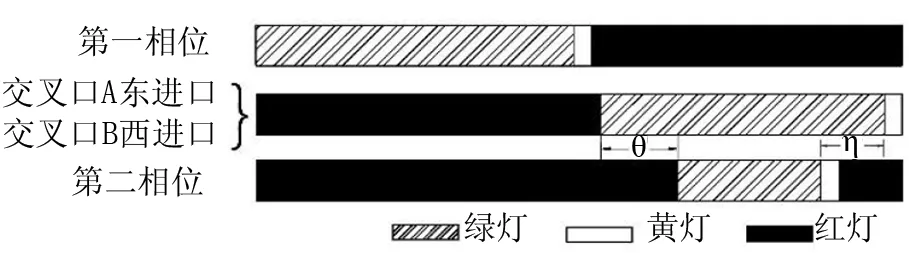
图7 相位设计配时图

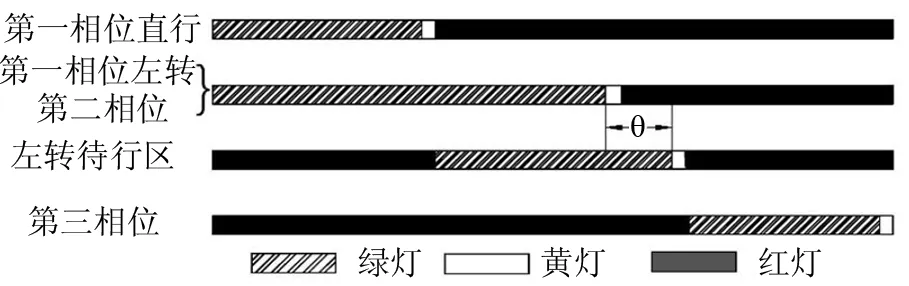
图8 搭接相位设计配时图

3.3 搭接相位设计

Ⅲ型跨河桥交叉口主路左转流量大,现行交通组织主要有两种:一种是主路东西进口直行通行时,左转车辆在进口停车线处停车排队;另一种是左转车辆驶入交叉口间路段并停车排队。前者保障了行车安全但增加了行车延误,后者虽在一定程度上缩短了行车时间,但是对向左转车流相互干扰,易诱发事故。鉴于此,首先对交叉口进行渠化,将交叉口间路段最内侧车道分别改造为对向车流的左转待行区,主路左转车辆利用该区域进行左转,消除了左转车流间的相互干扰。采用搭接相位设计,主路左转车流可充分利用直行绿灯时间驶入相应待行区排队,减少交叉口内的行车时间。

为保证主路左转车辆不发生排队溢出,在第二相位结束时存在相位差θ清空左转待行区内的车辆,θ计算方法同公式(1)。

4 案例分析

选择济南市西工商河路与师范路交叉口作为算例。西工商河路与师范路交叉口属于Ⅱ型交叉口,其中师范路双向四车道,一块板断面形式;西工商河路为南北走向的沿河道路,由西工商河分隔成为西工商河西路和西工商河东路,单车道。两交叉口交通关联性较强,高峰时期该交叉口经常因排队溢出而形成拥堵。交叉口现状流量见表2。

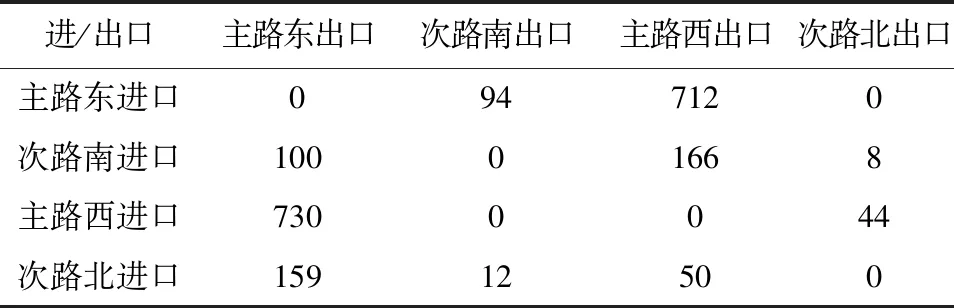
表2 交叉口流量表 单位:veh/h

以此为例,通过优化前后数据对比验证模型的可行性。已知条件如下:两交叉口间距L=42 m,主路绿灯时间为45 s,次路绿灯时间35 s,黄灯时间3 s。停车波波速1.84 km/h,启动波波速14.6 km/h。路段平均车速20 km/h。现状配时方案如图7所示,其中θ=0 s,η=42 s。

应用Ⅱ型相位差计算模型对该交叉口进行优化设计,优化结果对比如表3所示。从表中数据可以看出,配时方案优化后,增加了θ时长,使南北进口左转车辆能够完全驶出交叉口或在交叉口间路段排队,以免堵塞主路通行。与此同时,清空滞留车辆的η时长得以优化减少,整个周期时长大大降低。

表3 优化前后配时对比

利用VISSIM仿真软件设置检测器,从行程时间、排队长度和系统延误三方面,对案例进行仿真对比分析与评价,结果如图9、图10和表4所示。

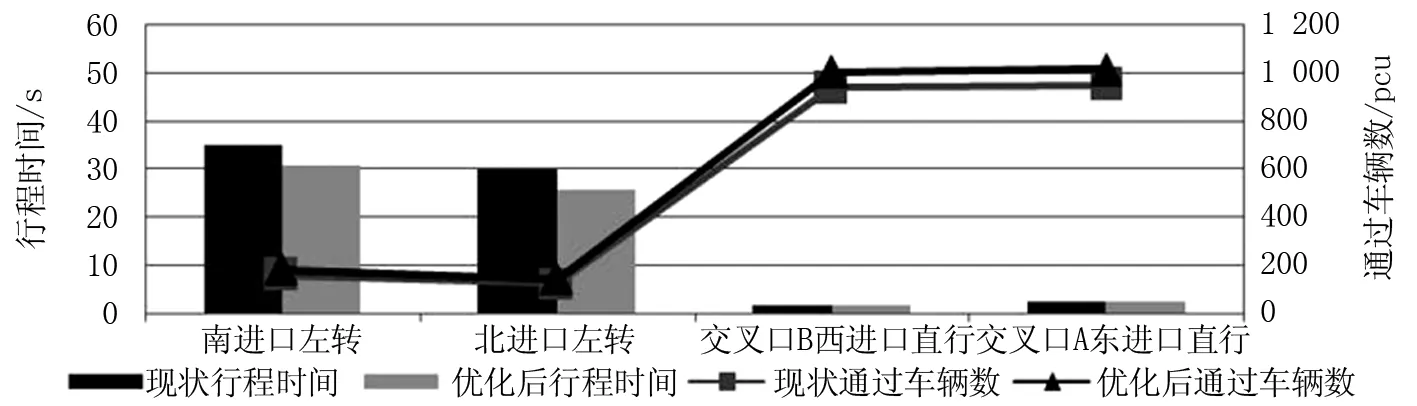
图9 行程时间对比

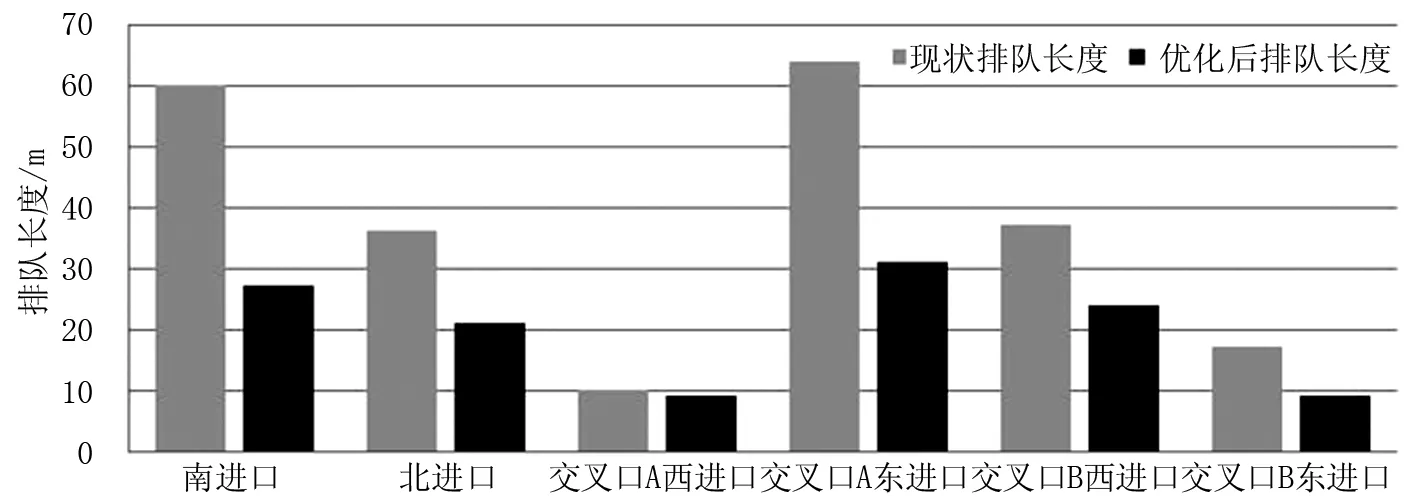
图10 排队长度对比

表4 系统平均延误和通行能力对比

由表4可知,实施协调控制策略之后,在不影响跨河桥交叉口主路直行车流行程时间的同时,南、北进口左转车辆行程时间有较大幅度降低,下降比例分别为13.27%和18.04%,进而提高了该方向的通过能力,通过车辆数分别上涨13.84%和15.32%,主路直行方向通过车辆数也因此增加约7%。各个进口排队长度均有不同比例的下降,尤其是跨河桥交叉口间路段,即交叉口A东进口和交叉口B西进口的排队长度,分别下降51.56%和35.14%,有效的避免了交叉口排队车辆溢流情况的发生。表4数据显示,优化后系统平均延误下降17.50%,整个交叉口系统通行能力提高8.02%,通行效率大大提升。

5 结 论

针对跨河桥交叉口间距短、关联性强,极易发生排队溢流的问题,将整个交叉口作为系统进行一体化设计。在剖析车流特性的基础上将跨河桥交叉口按车流运行规律归为3类,以消除冲突点为原则,避免排队溢出为约束,提高系统通行能力为目标,提出相应的协调控制策略,并推导了相位差的计算模型。运用VISSIM仿真软件对济南市西工商河路与师范路交叉口进行仿真评价,结果显示跨河桥交叉口间的排队长度明显减少,整个交叉口系统通行效率有较高提升,证明模型有效。