风电法兰接触界面不平整对螺栓疲劳寿命的影响研究

赵 伟 赵 达 马奔奔 唐 林

（东方电气风电股份有限公司风电研究设计院，四川 德阳 618000）

0 引言

高强度螺栓是风电领域常见的一种重要连接部件，螺栓的疲劳寿命对连接系统整体的安全性与稳定性有着极大的影响[1]，所以高强度螺栓一直是风电领域的关注重点。

据悉，近年某风场出现了叶片部位3#、4#叶根螺栓断裂的情况。现场检测发现，在螺栓断裂处，法兰接触端面存在0.05～1.2 mm的间隙，如图1所示。为了确定该间隙是否对结构强度及螺栓疲劳寿命造成影响，本文建立了考虑法兰初始缝隙和平整无缝隙两种情况的三维有限元仿真模型，对螺栓极限与疲劳进行了对比分析。最后，提出了一种初始缝隙加垫片的修补方案。修补后，螺栓的疲劳寿命显著提升到了平整无缝隙情况的效果。

图1 3#、4#叶根螺栓断裂位置示意图

1 有限元模型的建立

为了确定该间隙是否对结构强度及螺栓疲劳寿命造成影响[2]，本文建立了考虑法兰初始缝隙和平整无缝隙两种情况下的三维有限元仿真模型。

1.1 轴承的仿真

变桨轴承通常为八点接触盘转轴承，图2为典型的八点接触盘转轴承的截面示意图，共有4个接触对。轴承通常采用负游隙，滚道的半径比滚子半径略大，在轴承不受载荷的初始状态下，滚道和滚子有8个接触点，这8个接触点构成4个接触对，接触对1和3处于45°接触角，接触对2和4处于135°接触角。

图2 变桨轴承滚子滚道接触示意图

滚子如果用实体模拟会带来大量的实体网格以及滚子滚道接触单元，计算速度和收敛性会大受影响，滚子的模拟必须简化。如图3所示，link180单元具有独一无二的双线性刚度矩阵特性，这使其成为一个仅受拉或仅受压的杆单元，这里设置成仅受压的特性来模拟滚子和滚道的接触属性：滚子和滚道接触时传递法向的接触载荷，滚子和滚道分离时不传递载荷。通过一组link180单元来模拟一个滚子，就能很好地模拟该类轴承的非线性接触特性，以及接触角度变化和接触刚度变化特性。

图3 轴承滚子link180单元模拟示意图

1.2 螺栓的仿真

有限元模型中螺栓采用梁杆和实体组合建模形式，螺杆部分采用梁单元，螺母部分必须采用实体建模。螺杆部分采用梁单元如图4所示，螺母部分为A位置，另一侧螺纹啮合部分为B位置，0.5D为螺杆和螺母以及啮合部分的作用点位置。

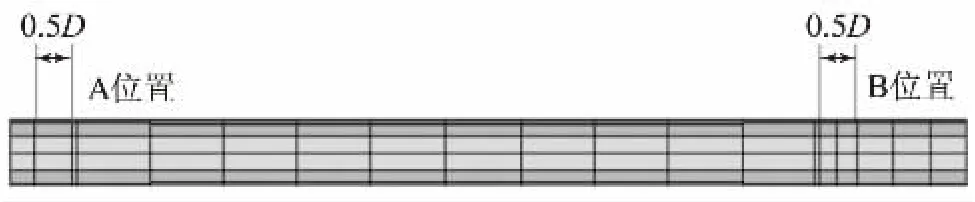
图4 螺杆梁单元建模

螺栓和螺母以及螺纹啮合部分采用载荷伞的方式连接，如图5所示，垂直方向为螺杆梁单元（Beam188），水平方向为啮合部位载荷伞连接梁单元组（Beam4），斜向为啮合部位杆单元组（Link8），并在螺杆单元中间位置施加向中心收缩的螺栓预紧力。

图5 螺栓连接详细示意图

1.3 整体仿真模型的建立

最终建立起的完整有限元模型如图6所示，整个模型共有141万单元，86万节点。变桨轴承和轮毂的连接面采用全约束，叶片上端施加弯矩载荷。整个模型接触关系定义为摩擦系数为0.3的标准接触。

图6 考虑法兰初始缝隙的三维有限元模型

2 极限和疲劳分析

2.1 预紧工况下初始缝隙的变形

法兰接触面平整和初始含有间隙两种情况下，在螺栓施加440 kN预紧力时，法兰之间接触位置的状态如图7所示。显然，接触面平整时，与轮毂端面完全接触，两个接触面的位移相同；当接触面存在间隙时，两侧端面变形不协调，由于预紧力的作用，缝隙会有一定的收缩。初始模型设置的最大间隙为1.25 mm，在预紧力的作用下，最大间隙变为0.92 mm。

图7 施加预紧力时接触面竖向位移

施加相同的预紧力440 kN，接触面平整时，各螺栓的预应力分布相同，最大值为743.2 MPa；接触面局部存在间隙时，螺栓除了承受预紧力，还承受因接触面变形引起的附加弯矩，其间隙位置处螺栓的最大应力值也较平整位置处大11 MPa，最大值为754.2 MPa，如图8所示。

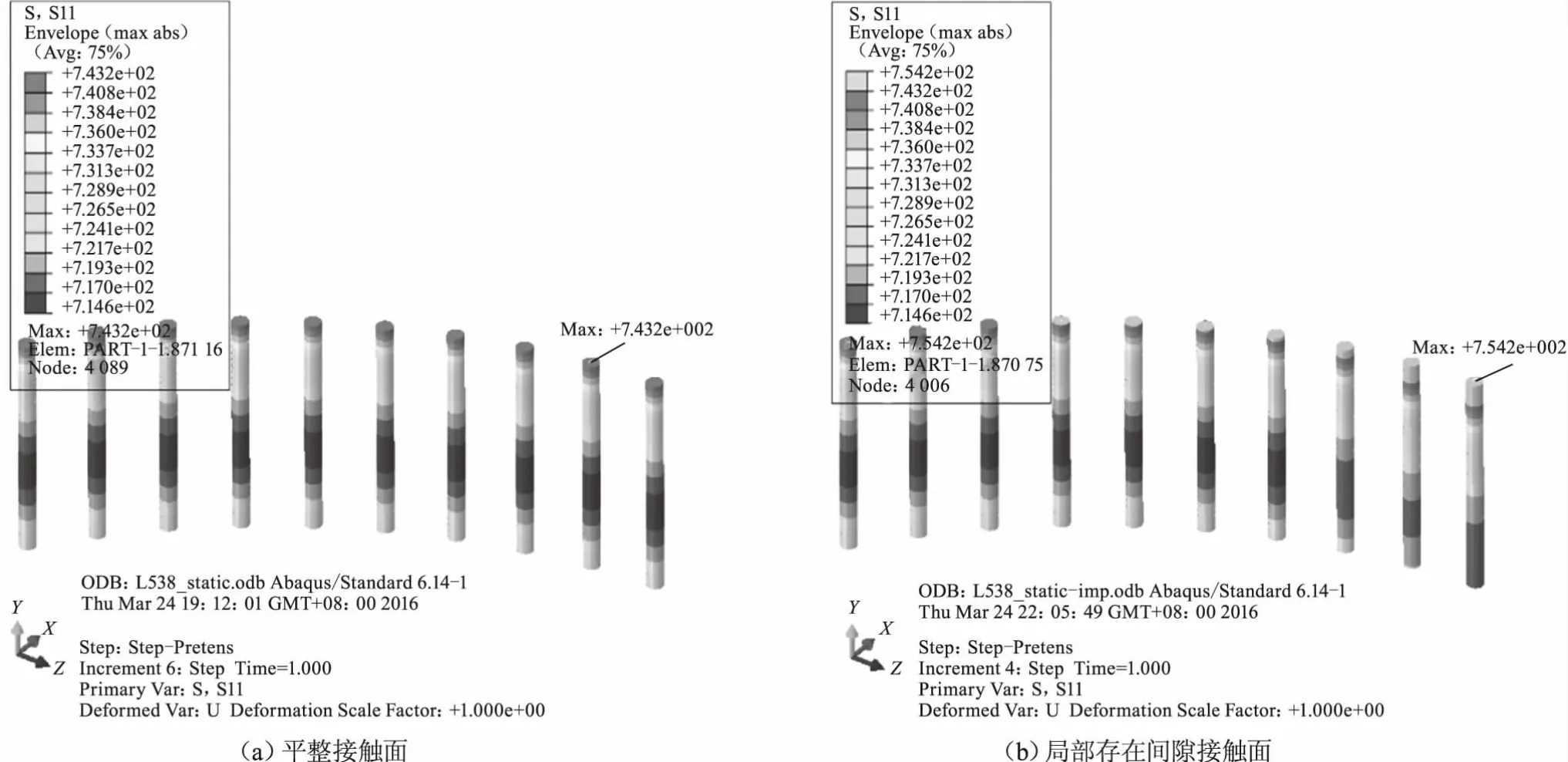
图8 螺栓预应力对比

2.2 弯矩1 000 kN·m下连接螺栓应力对比

变桨轴承和轮毂的连接面采用全约束，叶根弯矩1 000 kN·m。接触面平整时，螺栓的应力最大值为818.7 MPa；接触面局部存在间隙时，螺栓除了承受预紧力，还承受因接触面变形引起的附加弯矩，其间隙位置处螺栓的最大应力值也较平整位置处大53.2 MPa，最大值为871.9 MPa，计算结果如表1、图9所示。

表1 极限强度对比表

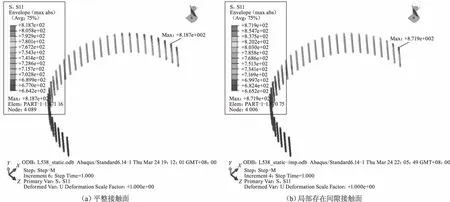
图9 弯矩1 000 kN·m下螺栓预应力对比

综上分析，在两种不同接触面的情况下，各部件极限强度均满足许用强度；当接触面局部含间隙时，各部件的应力值稍大，其连接螺栓的最大应力值比平整接触面的大53.2 MPa。

2.3 螺栓疲劳寿命评估

首先确定螺栓疲劳分析的有限元分析工况：第一步施加最小螺栓预紧力（螺栓的预紧力最小时，工作时相应的应力幅值也大，该方法保守且合理）；第二步在轮毂中心远程载荷点上施加MYZ，分12个方向（0°，30°，60°，…，330°），每个方向又分6个子步将MYZ逐渐施加到18 300 kN·m，这种加载方式同时考虑了载荷大小和载荷方向对螺栓应力的非线性影响。故螺栓疲劳分析的有限元工况数为12×6+1=73个，各载荷步及载荷子步载荷施加位置和载荷大小如表2所示。

表2 螺栓疲劳有限元分析时的载荷工况

螺栓疲劳分析的步骤如下：

（1）从各个有限元工况的分析结果中，针对每个螺栓，可提取MYZ大小和方向对螺栓应力（σaxial，σbending，1，σbending，2）的3个二维应力影响矩阵。

（2）在Matlab中将MYZ的时间序列，包括大小MYZ_M（t）和方向MYZ_D（t）在3个二维应力影响矩阵的基础上进行插值，得到每个螺栓危险截面A和B上的3个应力时间序列（σaxial（t），σbending，1（t），σbending，2（t）），MYZ_M和MYZ_D通过如下公式计算：

式中：d′为轮毂中心至主机架与发电机法兰连接面的距离，d′=3.82 m；d″为发电机重心到螺栓连接面距离，d″=0.718 m；m为发电机自重，m=166 t；g为重力加速度，g=10 m/s2。

（3）依据3个应力时间序列，在Matlab中得到螺栓应力截面圆上每隔30°的点（12个）应力时间序列σ（β，t）；主机架与发电机连接螺栓不仅承受轴向拉伸载荷，还承受弯曲载荷，故有必要对螺栓应力截面圆上的多个点进行疲劳计算。每隔30°的点的轴向应力时间序列如下：

其中，β=0°，30°，…，330°。

（4）通过Matlab程序，利用雨流计数法和Miner理论计算螺栓25年累积疲劳损伤。最终的损伤结果如表3所示，可以看出，平整接触面螺栓设计寿命最大损伤为0.91，满足25年累积疲劳损伤的设计需求；当局部存在初始间隙时，螺栓的最大损伤提高到了13.13，寿命缩短93.07%至1.9年。可见，接触端面存在间隙会显著降低该部位连接螺栓的疲劳寿命[3]。

表3 疲劳损伤对比表

3 初始缝隙消除方法

这里提出了一种加垫片消除法兰接触面初始缝隙的方法，如图10所示。

图10 初始缝隙消除有限元模型设置

为验证该方法的准确性，进行了0～10 000 kN·m弯矩下螺栓最大拉应力幅的对比测试。由图11可以看出，存在初始缝隙时，连接螺栓的载荷—应力幅曲线明显比平整接触面接触状态下的载荷—应力幅曲线高，显然，连接螺栓疲劳寿命也会显著降低。添加垫片进行修补后，连接螺栓的疲劳寿命有明显改善，载荷—应力幅曲线与平整接触面的载荷—应力幅曲线基本吻合，根据载荷谱计算所得的损伤因子小于1（表3），满足使用要求。

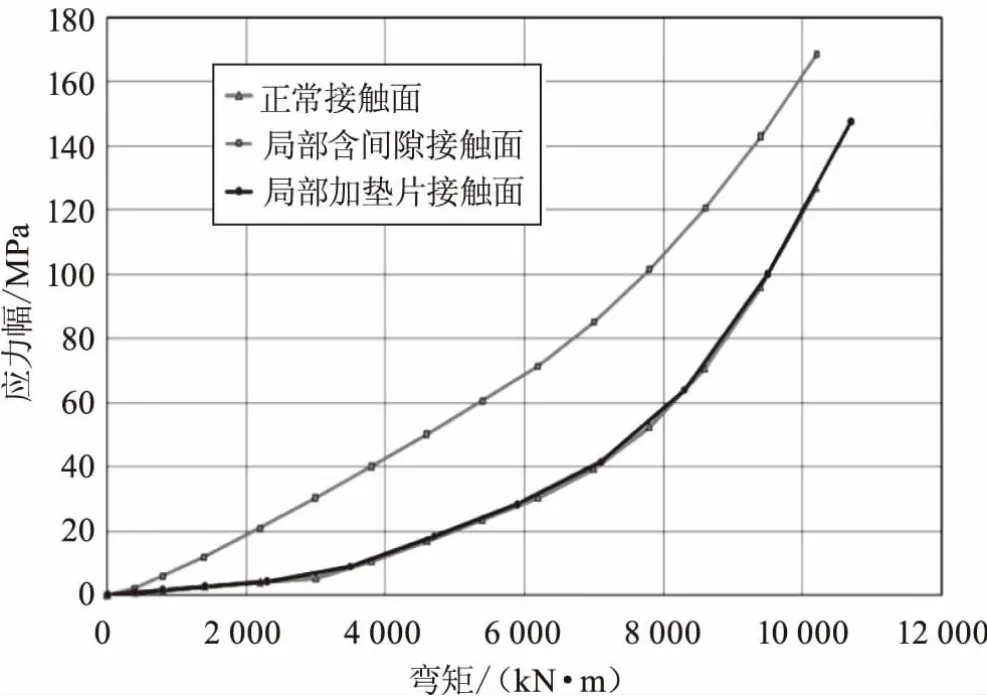
图11 正常接触面、局部含间隙接触面及加垫片修补方案下弯矩—螺栓最大应力幅对比曲线

4 结束语

本文借助有限元分析的手段对变桨轴承法兰接触界面不平整对高强度螺栓疲劳寿命影响的问题进行了研究。通过建立法兰接触面平整和局部含有间隙两种详细的三维实体模型，对比分析了螺栓的受载情况，发现接触缝隙会显著增大螺栓的最大拉应力，使其疲劳寿命显著下降。本文最后提出了一个接触界面之间增加垫片来消除间隙的方法，添加垫片进行修补后，连接螺栓的疲劳寿命有明显改善，载荷—应力幅曲线与平整接触面的载荷—应力幅曲线基本吻合。