改进粒子群优化算法的果园割草机作业路径规划
2023-11-09谢金燕刘丽星王潇洒
谢金燕 刘丽星 杨 欣 王 旭 王潇洒 陈 诺
(河北农业大学 机电工程学院,河北 保定 071000)
我国是水果种植大国,果园种植面积逐年增加,趋向规模化、现代化发展[1-2]。果园杂草过多影响果树生长,机械除草是当前经济效益较高的一种除草方式[3]。规范化种植的果园,果树排列整齐,行间留有较大间距,使得机械除草容易实现。与传统人力驾驶割草机在果树行间逐行往复除草的方法相比,采用农业机械自动导航技术对具有自主导航功能的割草机进行全覆盖作业路径规划,可显著提高割草机的作业效率,降低其作业成本,对果园生产管理更有益[4-5]
全覆盖路径规划是基于环境信息已知前提下,对覆盖固定区域的路径做出合理规划的路径规划方法[5]。Bochtis等[6]提出了一种B-patterns模型,将农机作业时对农田的全覆盖表示为加权图的遍历,寻找最优作业路线等效于寻找使总非工作距离最小的遍历序列。Hameed等[7]则在B-patterns模型的基础上,考虑使农机作业重叠区域最小化问题,提出了基于遗传算法的三阶段路径规划方法。Amalia等[8]以农机全覆盖作业时的工作距离最短为目标,提出了一种进化混合邻域搜索算法来求解不同作业场景下的路径优化问题。国内,孟志军等[9]提出了一种全区域覆盖路径优化方法,通过选择不同优化目标计算出农机最佳作业方向,以此生成沿该方向逐行覆盖地块的作业路径。黄小毛等[10]则考虑了跨行作业的情况,以转弯路径总长度最小为目标,将覆盖矩形农田的各个作业行的调度排序问题转化为经典的旅行商问题。罗承铭等[11]提出了针对四边形田块全覆盖的混合路径,同样对混合路径中的方向平行路径进行调度排优以减少非工作路径长度。现有的全覆盖路径规划研究常将路径规划问题转化为离散的组合优化问题,且主要应用在农田作业中,而对果园环境下的全覆盖路径规划还研究尚少。
不同于大田作业,果园由于果树行的存在而形成了固定的作业结构。果园割草机工作时只需沿着果树行方向从果园的一端到另一端、一行到另一行便可以完成整个果园的割草任务。割草机如何遍历各果树行完成割草任务,并使最终的工作路径最短,是典型的全覆盖路径规划问题[12]。目前,常使用元启发式算法解决此类问题[13]。PSO(Particle swarm optimization)算法是一种基于一群在N维空间的粒子,通过自身与群体的适应度值评价来更新其位置和速度从而探索空间内全局最优解的启发式群体智能算法,具有简单易实现,收敛速度快,搜索范围广等特点,但易陷入局部最优[14]。本研究拟构建割草机作业模型,将果园环境下的割草机作业路径规划问题转化为组合优化问题,并改进PSO算法进行求解,以期为果园环境下的农业装备全覆盖路径规划问题提供理论依据。
1 割草机作业路径特点分析
现代苹果果树更多地采用矮化密植技术种植,为有效发挥该技术优势,对果园建设提出了要求。园区选择较为平缓的坡地,果树株距为1.5~2.0 m,行距3~4 m,同时果树行前后留有地头便于机械化调头[15]。果园割草机正常作业时,每个果树行一般来回收割2次即可完成行间除草任务。大部分果园为了保墒、提温、抑制杂草生长,会选择顺着树行覆黑色地布。铺设地布处无杂草,割草机工作时无需考虑这部分。
规范化布局的苹果园,杂草多生长于果树行间,使得割草机的作业方向与果树行排列方向平行。割草机沿果树行方向行驶的路径可称为方向平行路径;当割草机割完一行杂草,在果园地头处转弯进入下一行,转弯时行驶的路径可称为衔接路径[16]。割草机工作时,方向平行路径与衔接路径交替出现,完成对果园的全覆盖。因此,割草机的工作路径由方向平行路径与衔接路径构成。果园环境确定时,方向平行路径长度一般是固定值。优化割草机工作路径时,不考虑方向平行路径,采用减少衔接路径长度的方式使割草机最终的总路径最短。
2 割草机作业模型构建
2.1 割草机作业行
除草时,割草机沿着果树行来回工作2次,每个果树行由此被割草机重新划分为2个作业行(图1)。
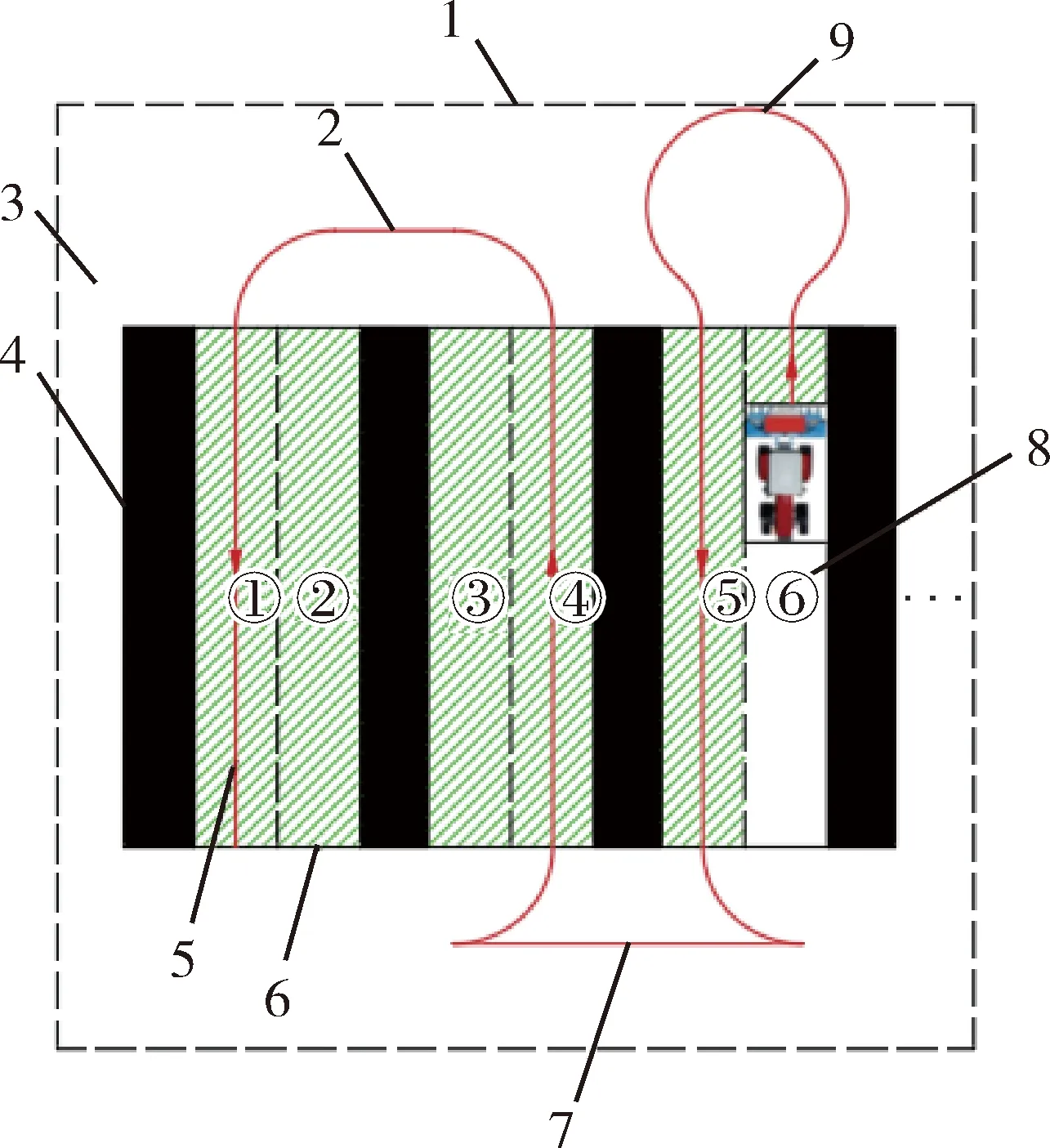
1.矩形果园;2.U型转弯;3.地头;4.地布;5.作业轨迹;6.作业行;7.T型转弯;8.作业行编号;9.Ω型转弯
对方向平行路径的调度优化可显著减少衔接路径的总长度,即地头总转弯距离[11]。当割草机工作参数及果园环境参数确定时,可对作业行进行调度排优来减少总转弯距离,即通过对各作业行间的合理排序完成对割草机作业路径的规划。不同的转弯策略产生的转弯路径不同,要计算总转弯距离,需对割草机作业时选择的转弯策略进行分析。
2.2 地头转弯距离
割草机完成一行割草作业后,需要在果园地头处转弯进入下一行。当具有自主导航功能的轮式果园割草机转弯时,通常使用阿克曼转向。根据割草机作业间距Lw与最小转弯半径r的大小关系,常用的转弯策略有Ω型、U型和T型[17](图2)。
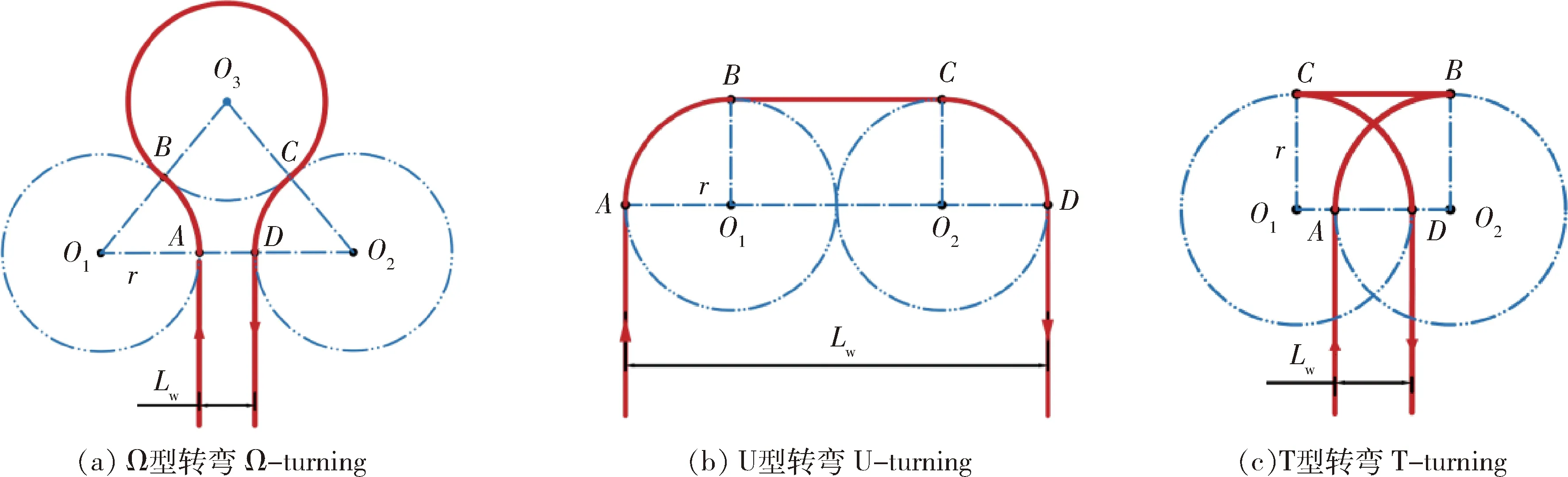
O1和O2为辅助圆圆心;A、B、C和D为转弯路径与圆O1、圆O2的切点;Lw为割草机的作业间距;r为最小转弯半径。
割草机在同一果树行内转弯时转弯路径中不包含地布,而在不同果树行间转弯时则需考虑包含的地布数,以便计算转弯距离。根据该特点,本研究改进Ω型、U型和T型转弯距离计算公式如下:
(1)
dU=(π-2)r+d(i,j)w+mLd
(2)
dT=(π+2)r-d(i,j)w-mLd
(3)
式中:dΩ表示Ω型转弯距离;dU表示U型转弯距离;dT表示T型转弯距离;r为割草机的最小转弯半径;i为当前作业行的编号;j为割草机转入的下一行的编号;d(i,j)为转弯时两作业行间的跨度,d(i,j)=|i-j|,i≠j;w为割草机的作业幅宽;m为转弯时所跨地布数;Ld为地布宽度。
设V={1,2,…,n}为割草机作业行编号的集合,n为总行数;dij为割草机从i行转入j行的转弯距离(∀i,j∈V),且dij=dji,dnn=0。割草机采用T型转弯时需要沿直线倒车,为简化割草机作业,只考虑Ω型转弯和U型转弯,转弯类型的判断方法如下:
(4)
根据作业行间的转弯距离dij构建距离矩阵D如下:
(5)
实际割草机转弯时并非严格按照上述转弯方式进行转弯,为方便计算,不考虑割草机实际转弯路径与理论转弯路径不重合所带来的转弯距离偏差。
2.3 数学模型
以割草机的作业行序列为变量,总转弯距离最小为目标函数,构建割草机作业路径优化模型如下:
1)定义变量:
(6)
式中:xij为割草机是否从i行转入j行的决策变量。
2)目标函数:
(7)
式中:dij为作业行i与j之间的转弯距离。
3)约束条件:
(8)
(9)
式中:a为割草机工作起始行编号;b为割草机工作结束行编号。
(10)
式中:|S|为集合S元素的个数。
式(8)~(10)表示每个作业行仅被割草机遍历1次,且割草机完成作业后不会回到起始行。
3 PSO算法改进
3.1 PSO算法求解离散问题分析
经典PSO算法[18]的核心是通过粒子间相互分享信息使粒子群体由无序转为有目标地向空间内的最优解方向移动,最终获得问题的解。N维搜索空间内,粒子i的位置为Xi=(xi1,xi2,…,xiN),速度为Vi=(vi1,vi2,…,viN),粒子i自身访问过的最佳位置为Pi=(pi1,pi2,…,piN),整个粒子群体访问过的最佳位置为Pg=(pg1,pg2,…,pgN)。粒子速度与位置的更新公式如下:
(11)
(12)
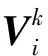
经典的PSO算法常用于在连续定义域上查找数值函数的最小值,割草机作业行的调度排优是离散的组合优化问题,求解时需对算法各部分重新定义[19-20]。
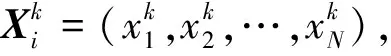
2)粒子的适应度值定义为割草机工作时的总转弯距离,适应度值越小代表粒子找到的作业路径越好。
4)针对离散问题,粒子位置的更新逐步进行,步骤如下:
①记录使粒子i由当前位置转变为最佳位置Pi、Pg的交换序列,在(0,1)范围内随机选取学习因子的值,按c1、c2的概率分别对能转换为Pi、Pg的交换序列进行保留;
②按惯性权重ω值的概率对当前调整序列进行保留;
③将保留的交换序列与调整序列融合,以此作为新的调整序列;
④利用更新后的调整序列对粒子i当前位置进行调整,得到下一次迭代的粒子位置。
3.2 PSO算法改进策略
3.2.1改进惯性权重
惯性权重ω的大小反映当前粒子i的速度受上一代粒子的影响程度,是PSO算法的重要参数。现有的惯性权重模型有3种:常数、时变惯性权重及自适应惯性权重。为找到全局最优解,与静态值相比,动态变化的ω寻优效果更好[21]。本研究基于线性递减惯性权重[22]提出一种非线性递减惯性权重,表达式为:
(13)
式中:Tmax为算法的最大迭代次数;k为当前迭代次数。
图3示出线性与非线性递减惯性权重随搜索进程的变化。可见,相比于线性递减惯性权重,提出的非线性递减惯性权重使ω值在搜索前期较大,加强粒子的全局搜索能力;在搜索后期较小,加强粒子的寻优能力,以便获得更好的最优解。

图3 线性与非线性递减惯性权重随搜索进程的变化
3.2.2改进学习因子
学习因子(c1、c2)决定了粒子向自身及群体访问过的最佳位置靠近的概率,设计得当,将大大提高寻优效率。文献[23]提出了一种时变学习因子:在搜索初期,使控制粒子向自我学习的因子c1值较大,向群体学习的因子c2值较小,便于粒子全局探索;在搜索后期则相反,便于粒子专注寻优。因此,本研究设置学习因子为所提出的非线性递减惯性权重的三角函数,使c1随搜索进程递减,c2随搜索进程递增,同时使PSO算法的3个参数整合为一体,提高算法优化过程的均匀性,具体表达式如下:
c1=sinω
(14)
c2=1-sinω
(15)
学习因子c1、c2随搜索进程的变化见图4。
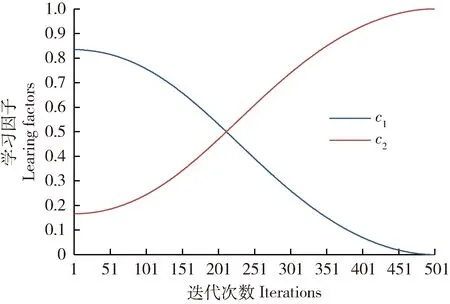
图4 学习因子c1与c2随搜索进程的变化
3.2.3粒子扰动
随着迭代次数的增加,粒子群体逐渐向同一目标区域靠近,容易陷入局部最优,失去多样性。为此,本研究使用交换操作对处于最佳位置处的粒子进行轻微扰动,增加粒子跳出当前局部最优的可能性,以便粒子寻找更好的作业路径。
交换过程为:假设粒子i经过迭代更新后获得的最佳作业行序列为2→5→8→10→7→4→1→3→6→9,随机选取两个作业行进行位置交换,如作业行3和5,则交换后的作业序列为2→3→8→10→7→4→1→5→6→9。作业行序列完成交换后将产生新的作业路径,计算当前新路径的适应度值,并与交换前的适应度值进行对比。若新路径较优,则保留新路径,否则维持原有路径不变。
3.3 IPSO算法实现
本研究提出的IPSO(Improved particle swarm optimization)算法求解果园割草机作业路径规划问题的具体步骤如下:
1)输入果园环境参数及割草机工作参数,构建距离矩阵D。
2)设置算法参数,随机产生粒子群初始位置和速度,计算初始位置的适应度值,将初始位置作为各粒子的最佳位置并挑选出群体中的最佳位置。
3)更新惯性权重、学习因子、粒子位置及适应度值。
4)将更新后各粒子位置的适应度值与其访问过的最佳位置的适应度值进行比较,若当前位置的适应度值更小,则保留其为最佳位置。
5)使用交换操作对处于最佳位置的粒子进行扰动,以便粒子跳出局部最优。
6)更新整个粒子群体的最佳位置,并记录路径。
7)判断当前迭代次数是否达到最大迭代次数。若是,算法终止运行,输出最优作业路径,否则转至步骤3)。
4 仿真试验分析
为验证不同作业行数和割草机工作参数条件下,IPSO算法解决割草机作业路径优化问题时的优化性能,以总转弯距离最小为优化目标,使用Matlab R2020b软件进行仿真试验。试验评价指标为总转弯距离减少率(IPSO算法与PSO算法求解出的最优路径的总转弯距离差值的百分比)、算法收敛速度(寻优迭代次数)和算法耗时。
4.1 不同作业行数下作业路径优化结果分析
使用PSO算法、IPSO算法分别对作业行数为20、40、50、70、80和100行的6类果园进行作业路径优化试验。结合常见果园与割草机特点,设置割草机工作参数:作业幅宽w=0.9 m,最小转弯半径r=2 m;设置果园地布宽度Ld=2 m。设置粒子规模为500,迭代次数500;IPSO算法中,ωmax=1,ωmin=0;PSO算法中,ω=0.5,c1=0.7,c2=0.2。PSO算法属于概率寻优,每次寻优结果不同。因此,每类果园取20次运行结果的平均值作为最终优化结果(表1)。可见,针对选取的6种不同作业行数的果园,相同试验条件下,与PSO算法相比,IPSO算法耗时平均增加约1.0~2.5 s,但均能找到总转弯距离更少的作业路径,总转弯距离减少率为7.52%~32.72%。
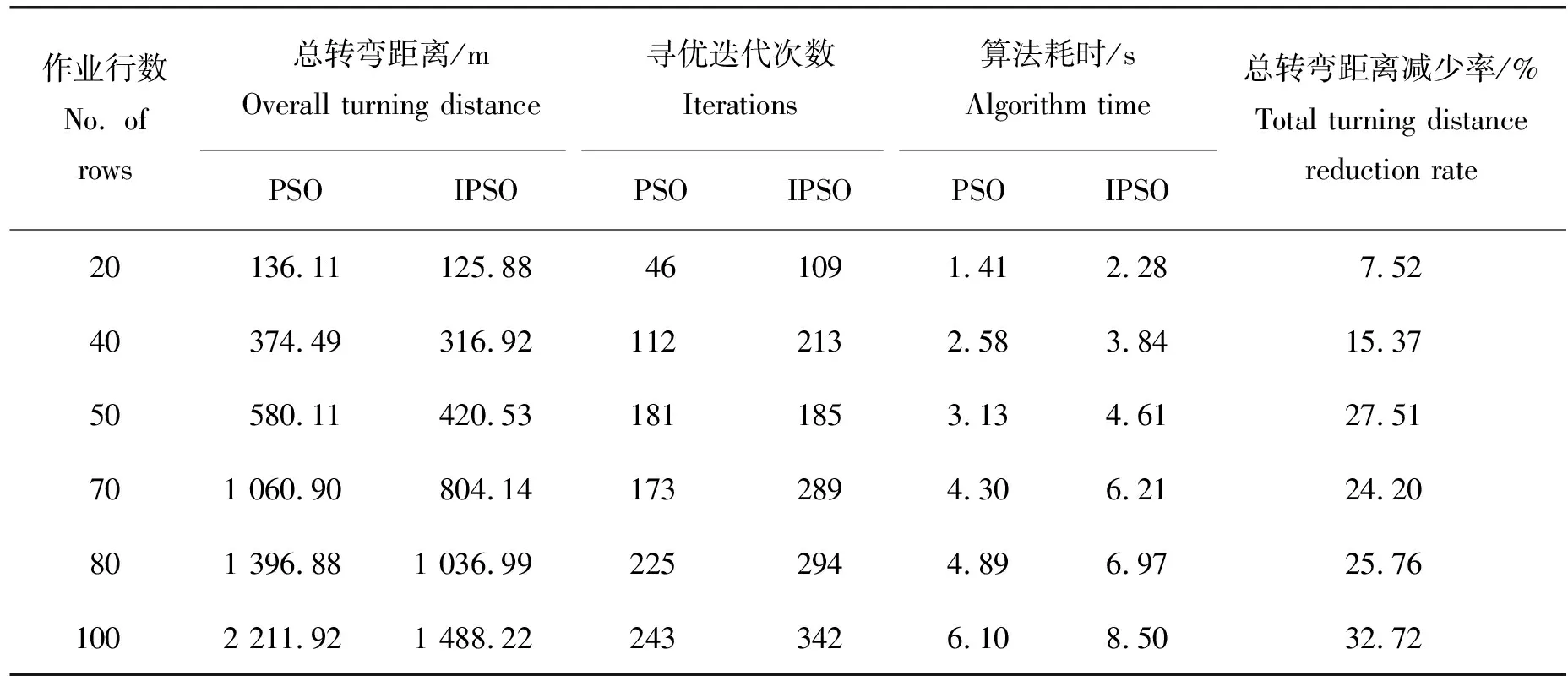
表1 不同作业行数下PSO与IPSO算法寻优结果
选取作业行数为40、70和100行的3类果园,进行算法寻优对比(多次运行取平均值),结果见图5:PSO算法与IPSO算法运行过程稳定,经过多次迭代计算后最终均能找到最优路径且结果趋于稳定;迭代过程中,IPSO算法的收敛速度较慢,但最终的寻优结果均优于PSO算法,且增加作业行数,IPSO算法减少的总转弯距离增大。
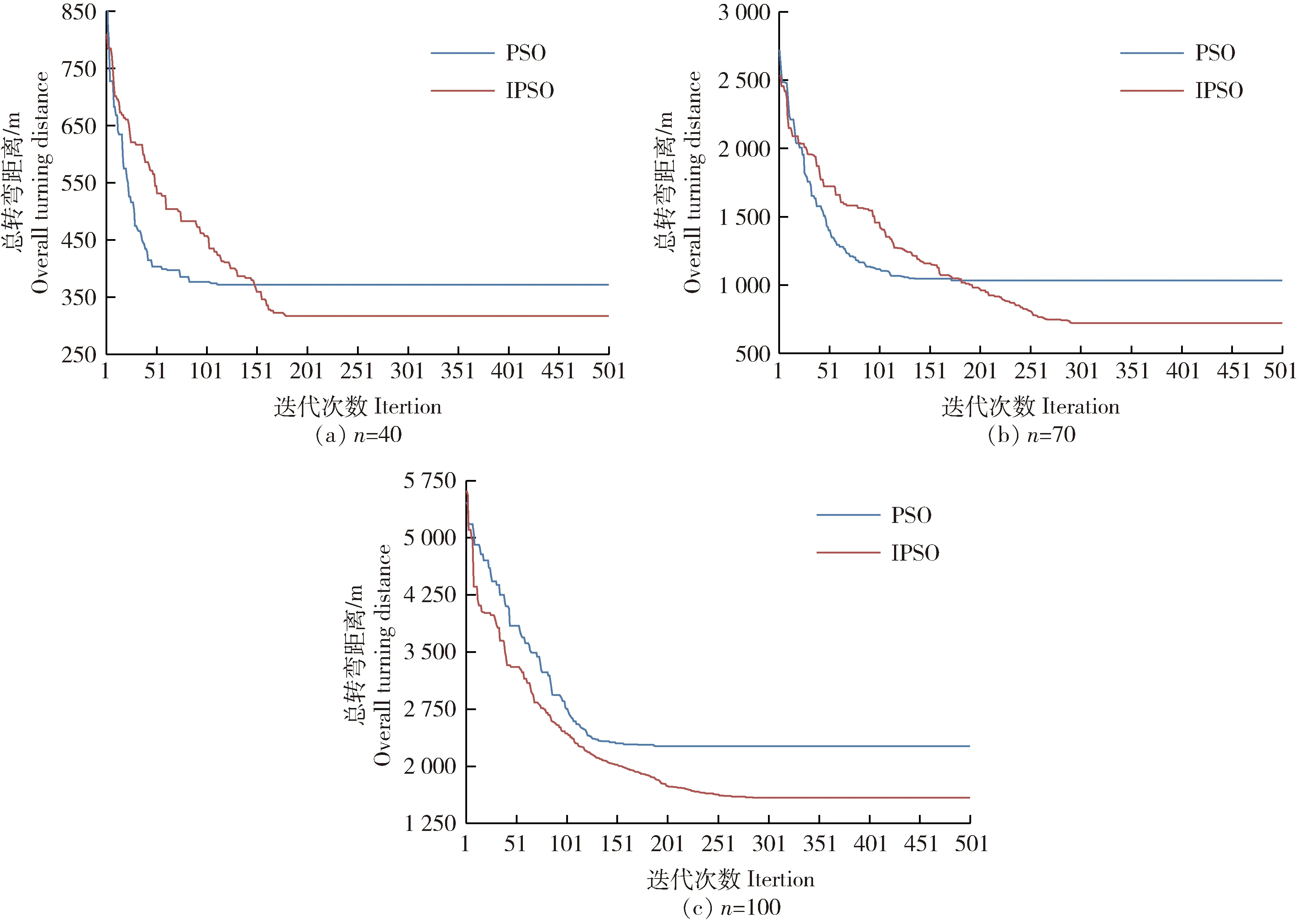
图5 不同作业行数(n)下PSO与IPSO算法寻优过程对比
随着作业行数的增加,寻找最优作业路径的难度呈指数增长。IPSO算法采用改进的惯性权重和学习因子,并对处于最佳位置处的粒子进行轻微扰动,使粒子群能更广泛地搜索解空间,避免了因过早陷入局部最优而停止搜索。与PSO算法相比,IPSO算法虽收敛速度较慢,但能够在大规模搜索的问题中找到更好的最优解。
4.2 不同割草机工作参数下作业路径优化结果分析
保持果园环境参数及算法参数不变,选择不同作业幅宽w、最小转弯半径r的割草机进行作业路径优化试验,并取20次运行结果的平均值作为最终优化结果,见表2。可知,对于不同工作参数的割草机,相同试验条件下,与PSO算法相比,IPSO算法均能找到总转弯距离更少的割草机作业路径。对比不同作业幅宽或最小转弯半径下的总转弯距离,结果显示:当作业幅宽或最小转弯半径减小时,总转弯距离减少。
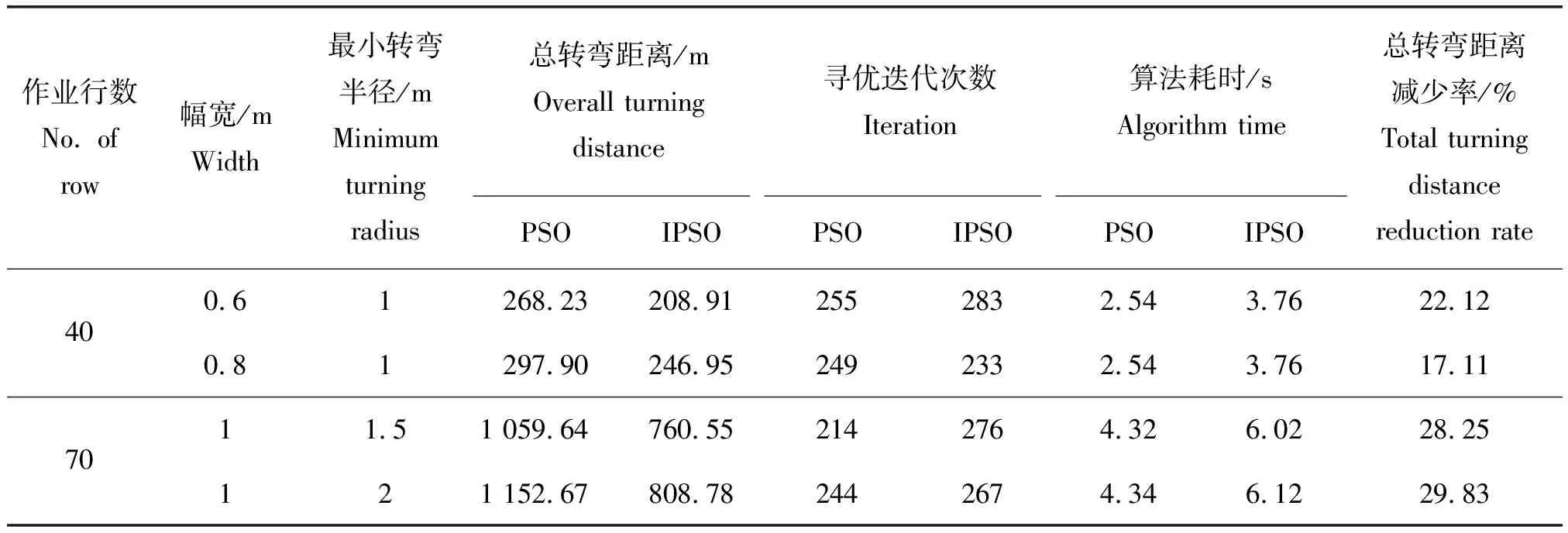
表2 不同割草机工作参数下PSO与IPSO算法寻优结果
通过以上仿真试验,表明了IPSO算法在求解割草机作业路优化问题时的有效性及普适性。
5 田间试验验证
为验证提出的IPSO算法解决割草机作业路径优化问题时的实用性,在标准苹果园内进行田间试验。
1)试验场地:河北省保定市顺平县顺农果品现代农业园区的某一矩形果园。经实地多次测量取平均值,获得果园环境参数为:作业行数30行、行间距4 m、地布宽度Ld=2 m。
2)试验设备:由强视(上海)科技有限公司生产的G33遥控割草机,割草机在试验园内的工作场景见图6。

1.地布;2.作业行编号;3.G33遥控割草机;4.作业行
3)试验评价指标:试验过程中受设备性能、果园路况及人工操作等多方面因素影响,割草机实际行走轨迹与理论计算偏差较大,故使用作业过程中的油耗率g作为评价指标,表达式如下:
(16)
式中:H1为试验前割草机油箱的油量高度;H2为试验后割草机油箱的油量高度;H3为割草机加满油时油箱的油量高度,测得为32 cm。
4)试验过程:①对H1进行测量并记录;②人工遥控G33割草机按照传统逐行割草的方式进行试验;③对H2进行测量并记录;④重复步骤①、②和③,依次对PSO算法、IPSO算法生成的作业路径进行试验。
试验结果见表3。可知,割草机采用算法求解的作业路径比采用传统路径节省油耗,采用IPSO算法求解的作业路径时油耗最小,比传统方法节约 22.51%,比PSO算法节约1.57%。由此,表明了IPSO算法的实用性。
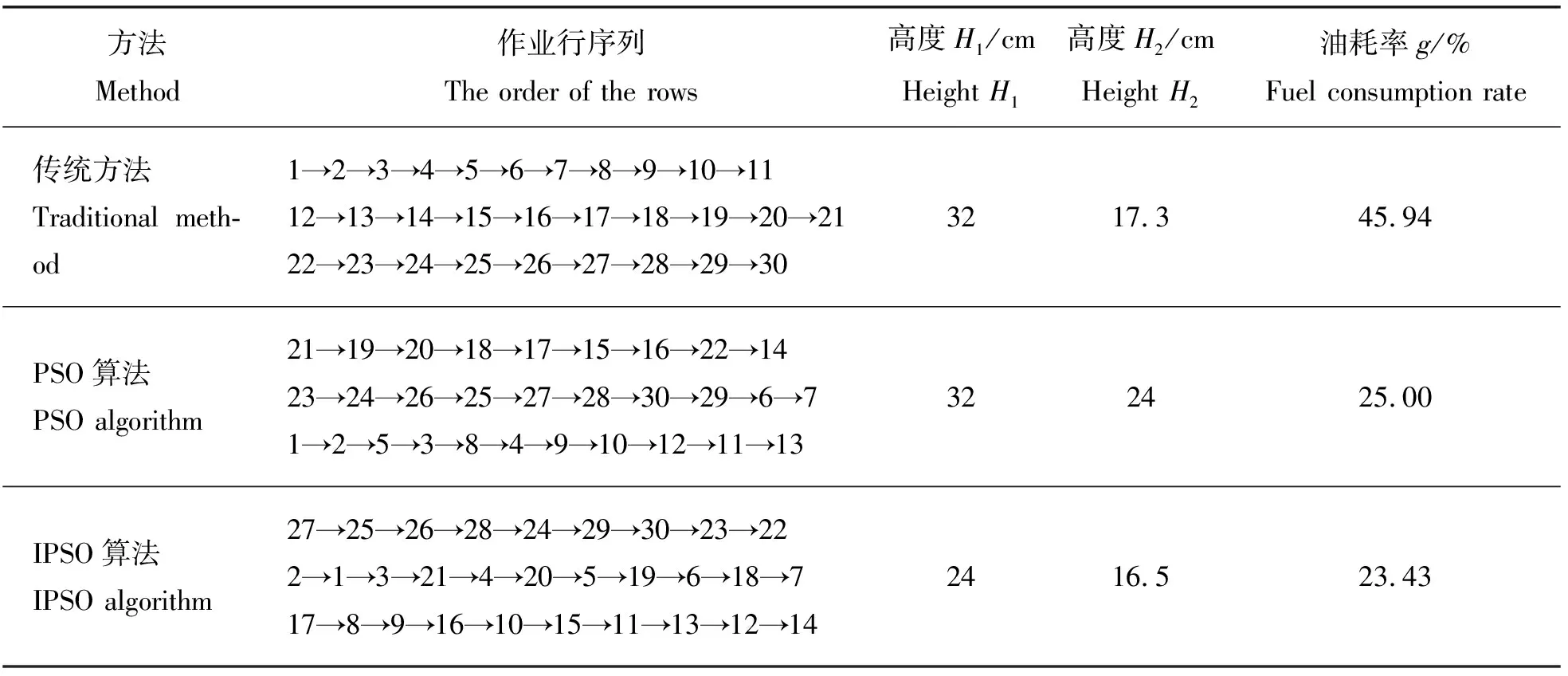
表3 不同作业路径下割草机的油耗结果
6 结 论
本研究针对果园割草机作业路径规划问题,构建了以总转弯距离最小为优化目标的割草机作业模型,并提出一种IPSO算法求解该模型,主要结论如下:
1)提出的随搜索进程非线性动态变化的算法参数及对处于最佳位置的粒子进行轻微扰动的策略能够有效增强PSO算法的寻优能力。不管作业行数或割草机工作参数如何变化,相比于PSO算法,IPSO算法总能找到总转弯距离更少的作业路径。
2)作业行数增加时,与PSO算法相比,IPSO算法减少的总转弯距离增大;保持作业行数不变,减小割草机的作业幅宽或最小转弯半径可减少总转弯距离。
3)割草机实际作业情况下,采用算法规划的作业路径比采用传统路径节省油耗。
此外,IPSO算法求解组合优化问题时的效率相对较低,下一步可以改进其他群体智能算法求解该类问题,以获得更优的割草机作业路径。果园实际生产中离不开机械化操作,果园智能装备路径规划问题还需进一步研究。
