基于VMD-AHA-LSTM 的短期电力负荷预测

穆昱壮，车浩然，夏伟峰，张家豪

（1.海南电网有限责任公司三亚供电局，海南 三亚 572099；2.国电电力朝阳热电有限公司，辽宁 朝阳 122000；3.沈阳工程学院 自动化学院，辽宁 沈阳 110136；4.国家能源集团辽宁电力有限公司沈西热电厂，辽宁 沈阳 110002）

准确地预测电力负荷能够辅助电力部门制定出合理的发电和用电计划，保障电网安全稳定运行［1-2］。然而，随着大规模新能源的并网，电力负荷多样性的不断增加，如何进一步提高短期电力负荷预测的准确性，也成为了众多学者研究的重点。

在当前常见的预测模型中，LSTM 在短期负荷预测时有着收敛快、预测准确度高等优点而被广泛应用［3-5］。由于隐含层节点数和学习率等超参数的选择不同，这就导致了模型的预测效果存在着巨大的差异。为了提高模型效果，文献［6］为寻找LSTM 模型的最优参数，引入了粒子群算法进行优化，仿真结果显示：相较于未经优化的模型，该模型的效果更好，然而粒子群算法中由于参数权重固定，导致算法陷入局部最优，影响优化效果。文献［7］采用了麻雀算法进行寻优，仿真结果表明：经过优化后的LSTM 模型准确度更好，但其也存在局部搜索能力较差的问题，易陷入局部最优。相较于传统优化算法，文献［8］采用了AHA 对模型进行寻优，其仿真结果表明了该算法寻优效果更好，全局搜索能力更强。因此，本文采用AHA 算法对LSTM模型进行优化。

为了更好地发掘出电力负荷历史数据中存在的信息，减少外部噪声干扰，提高预测精度，目前多采用数据分解的方式对负荷数据进行处理［9］。文献［10］采用经验模态分解（EMD）对原始数据进行了处理，经过处理后的预测结果相较于未处理的情况有了较大提升，但EMD存在模态混叠现象，也会造成准确度下降。为了解决此问题，本文采用能克服此问题的VMD对数据进行处理。

综上所述，为了提高短期电力负荷的预测准确度，本文提出了一种基于VMD-AHA-LSTM 的预测方法。该方法首先通过VMD 分解对原始数据进行处理，减小数据噪声，然后通过AHA 对LSTM模型隐含层神经元数与学习率进行寻优，最后将分解数据送入到优化后的模型中进行预测，并对结果进行重组，得到最终预测结果。

1 算法原理

1.1 人工蜂鸟算法

1）引导觅食

在引导觅食过程中，蜂鸟会引导前往最高访问级别的食物源处，然后在这些食物源中挑选出花蜜补充效率最好的作为目标。当目标确认后，蜂鸟开始前往目标点觅食，在搜寻过程中，利用AHA算法对3种飞行方式进行建模。

轴向飞行定义如下：

式中，randi([1,d])表示生成一个从1 到d的随机整数。

对角飞行数学模型如下：

式中，randperm(k)表示建立一个从1 到k的整数随机序列；r为（0，1］的随机数。

全向飞行的定义如下：

模拟引导觅食行为和候选食物源的数学方程如下：

式中，xi(t)为在第t次迭代时第i个食物源的位置；xi,tar(t)为第i只蜂鸟计划访问的目标食物源的位置；a为一个服从标准正态分布的引导因子。

第i个食物源的位置更新如下：

式中，f(⋅)表示函数适应度值。

2）区域性觅食

当蜂鸟到达目标点并吸食花蜜之后，存在一定概率不会继续访问现有食物源，而是去选择自己所在区域的附近寻找新的食物源，新食物源可能比之前的食物源更好。通过模拟蜂鸟在新食物源中的局部搜索与该区域性觅食方案的公式如下：

式中，b是服从标准正态分布的区域性觅食因子。

3）迁徙觅食

如果蜂鸟之前常去的区域出现食物匮乏时，它们就会向较远的地方进行迁徙，以寻找更好的食物源，这种寻找新区域的公式如下：

式中，xwor为种群中匮乏的食物源。

上述优化模型的整体流程如图1所示。

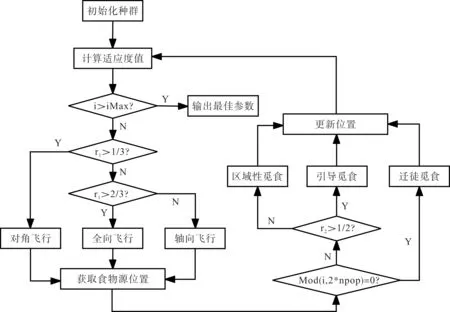
图1 AHA算法流程

1.2 VMD

VMD 作为时频分析方法，其认为任意信号都能由多个中心频率与带宽一定的信号所构成。相对于EMD 分解，VMD 能够克服模态混叠造成的影响，降低时间序列数据的复杂程度，使其平稳化并得到多个分量，适用于分解非线性和非平稳性数据。

1.3 LSTM

传统的循环神经网络（RNN）在处理长期数据时效果不理想，会出现梯度消失等问题，影响预测效果。因此，为了解决此问题，一些学者在RNN 的基础上提出了LSTM 模型，通过添加3个门对RNN存在的问题进行改善，LSTM 模型的基本结构如图2所示。

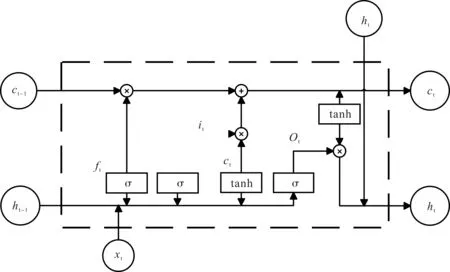
图2 LSTM网络结构

各个模块所对应的表达式如式（8）～式（13）所示：

式中，ft、it、ot分别是遗忘门、输入门和输出门；ct、ci、ht分别表示输入节点、状态单元和中间输出的状态；ht-1与xt表示中间输入状态；W表示各门的矩阵权重；⊙表示向量中元素按位相乘；tanh 与σ表示激活函数；b表示各门偏置向量。

2 模型搭建

考虑到原始负荷数据的复杂性及波动性，对原始负荷数据进行VMD 分解，模型流程如图3所示，具体步骤如下：

图3 模型流程

1）输入原始数据，采用VMD 算法对负荷数据进行处理，将其分解为多个不同分量；

2）通过AHA 优化算法寻找模型最佳参数，将各模态量输入到优化后的LSTM模型中进行训练；

3）将各个模态量的预测结果进行重构，得到最终的预测结果。

3 算例分析

图4 为我国南方某市2016 年1 月真实负荷数据，数据间隔为15 min，每日96 条，共计2 976 条负荷数据。采用最后一天数据作为测试结果，之前数据作为训练集送入到BP、RBF、LSTM、AHALSTM 和本文所提出的模型中进行训练，最后将本文所提出的模型与其他4种模型进行对比。

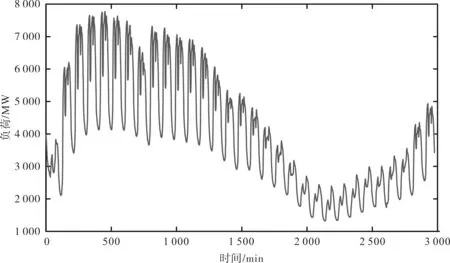
图4 原始电力负荷数据

数据分解结果如图5 所示，从图中可以看出：相较于原始数据，经过分解后的数据随机性明显减小，数据波动逐渐趋于平稳，IMF5也显示出原始数据整体的变化趋势。

图5 VMD数据分解

为了验证本文所提出模型的优越性，分别将其与BP、RBF、LSTM和AHA-LSTM模型进行对比，各模型预测结果的对比情况如图6所示。

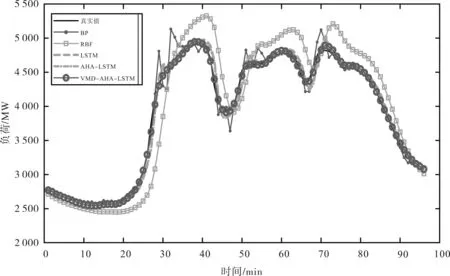
图6 各模型预测结果

从表1中可以清楚地看出：VMD-AHA-LSTM模型相较于BP模型，MAE减小42.1127MW，RMSE减小80.6135MW，MAPE减小0.9857%；相较于RBF模型，本文模型的MAE减小242.8706 MW，RMSE减小303.5504MW，MAPE减小6.0505%；相较于LSTM模型，本文模型的MAE减小38.9665 MW，RMSE减小59.8727MW，MAPE减小0.9315%；相较于AHA-LSTM模型，本文模型的MAE减小30.2694MW，RMSE减小56.0184MW，MAPE减小0.7384%。综上所述，本文所提出的VMDAHA-LSTM模型在各个指标的对比中效果最好，误差最低，准确度最高，预测值与真实值最为接近。

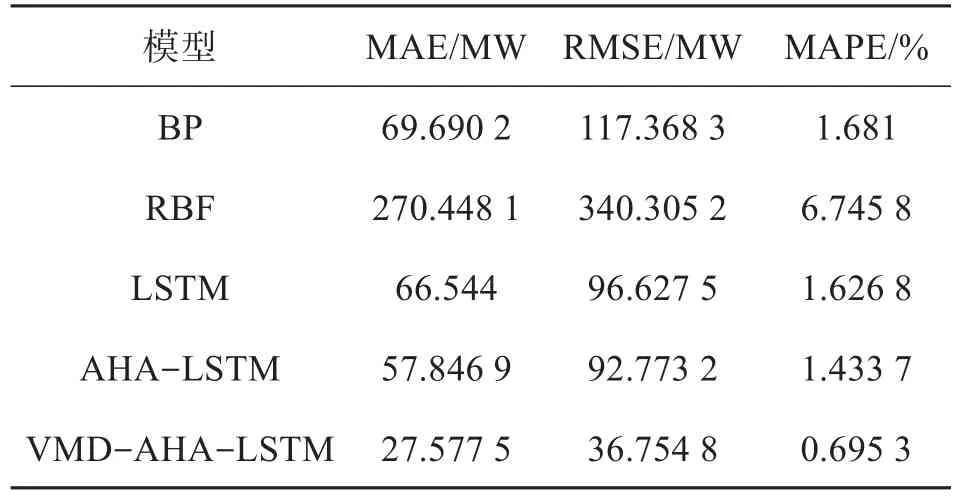
表1 预测结果评估

从图6中可以看出：4种对比模型和本文提出的模型都能对负荷进行较为有效的预测，整体的预测曲线与真实曲线基本吻合，但相比其他模型，本文所提出模型的预测结果更接近真实值，具有较高的预测精度。

为了验证所提出模型的预测效果，本文分别采用根均方差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）作为评估指标对模型进行评价，各模型评估指标结果如表1所示。

4 结语

针对当前复杂原始负荷数据导致的预测难度较大、准确度欠佳等问题，本文设计了一种基于VMD-AHA-LSTM 的短期电力负荷预测模型。首先，采用VMD 对负荷数据进行分解处理，将非平稳数据分解成多个相对平稳的分量；其次，采用AHA 算法对LSTM 模型进行优化，提高模型的预测精准度；最后，采用优化后的模型分别预测各分量值并将其重构，得到最终的预测结果。以我国南方某巿真实数据为例，通过与不同预测模型的预测结果进行对比，得出本文所提出模型在各指标对比中均优于其他模型，预测效果最好。