矿区断裂分形特征及其与冲击地压相关性分析

张满仓,兰天伟,袁永年,张顺峰,王顺翔

(1.国能神东煤炭集团有限责任公司 布尔台煤矿,内蒙古 鄂尔多斯 017200;2.辽宁工程技术大学 矿业学院,辽宁 阜新 123000;3.国家能源集团乌海能源公司 内蒙古利民煤焦有限责任公司,内蒙古 鄂尔多斯 016064;4.辽宁工程技术大学 鄂尔多斯研究院,内蒙古 鄂尔多斯 017010)

自Mandelbrot B B阐述了分形与分维的概念以来,分形维数就成了定量描述分形几何不规则特征的重要参数,并逐渐演化成一门新学科“分形几何学”[1].分形几何已在地貌学、岩石结构、矿床沉积评价、地质灾害等多个学科领域得到了广泛应用[2-5].

崔中良等[6]对川滇黔断裂构造进行分形几何研究,探讨断裂构造分形几何特征与成矿空间分布的关系,阐述了断裂构造分形几何对成矿预测的意义;张渊等[7]对敦煌多坝沟地区的线性构造进行遥感解译,利用分形几何原理求取线性构造分形维数,并将其作为找矿预测的指标;蒋超等[8]基于分形理论确定了广西大瑶山地区热液矿成矿的断裂构造分维临界值,分别给出铅、铜、金等成矿预测分形维数临界值;李飞等[9]研究招远地区的不同方向断裂分形特征,确定NNE和NE向断裂对矿产的控制作用较大;施国栋等[10]计算了安徽省的矿点、水系和断裂的分形维数,并分析三者的分形维数与成矿控矿的定量关系.上述研究多是将分形几何应用于断裂构造成矿、控矿,而且研究分形的尺度较大.冲击地压是煤矿严重的动力灾害之一[11].冲击地压发生机理复杂,影响因素较多,而断裂构造是冲击地压发生的重要地质因素[12],甚至对冲击地压有控制作用[13-14].在矿区角度下探讨断裂构造分形维数与煤矿动力灾害相关关系的文献较少,而且断裂分形维数与冲击地压的相关性研究还处于空白阶段.

黑龙江东部的鹤岗南部矿区和东荣矿区冲击地压灾害严重.因此,本文以鹤岗南部矿区和东荣矿区为工程研究背景,以地质动力区划确定的断裂构造为研究对象,基于分形几何原理,开展系统分形几何研究,对比分析各矿区、矿井的断裂分形几何特征,初步探讨不同矿区、矿井的断裂分形维数与冲击地压发生次数、位置之间的相关性,为深入研究断裂分形维数与冲击地压发生尺度、震级、能量等特性之间的关系奠定基础.

1 矿区地质构造

1.1 区域地质背景

鹤岗南部矿区和东荣矿区位于黑龙江东部地区,该区域发育有多条大型断裂,主要包括敦化—密山断裂、依兰—伊通断裂,断裂为NE走向;大和镇断裂、牡丹江断裂,断裂为近SN走向;同江—跃进山断裂,断裂为NNE走向.其中敦化—密山断裂和依兰—伊通断裂是郯庐断裂北段的两条重要分支,依兰—伊通断裂周边形成了汤原断陷、方正断陷、绥滨坳陷、佳木斯盆地、鸡西盆地、鹤岗盆地等多个新生代断陷盆地,如图1所示.鹤岗南部矿区处于鹤岗盆地,东荣矿区处于绥滨坳陷.

图1 黑龙江东部主要断裂及盆地分布

依兰—伊通断裂带是郯庐断裂带的北延断裂之一,该断裂南起辽宁省开原市,北至黑龙江省鹤岗市萝北县,并向北延伸至俄罗斯.断裂为NE走向,宽度为10～15 km.自1975年以来,根据地震学仪器记载,该断裂带附近共发生331次2.0级以上的地震,其中3.0级以上的地震76次.这表明依兰—伊通断裂带为活动性较强的断裂,区域构造运动较为活跃,对鹤岗盆地和双鸭山-集贤盆地的构造活动有一定的影响.从地质动力环境分析,依兰—伊通断裂及其活动性对鹤岗南部矿区和东荣矿区煤矿冲击地压具有重要影响.

1.2 矿区断裂构造划分

地质动力区划是以煤矿开采的工程块体为研究对象,根据地形地貌的基本形态和主要特征决定地质构造形式的原理,通过对地形地貌的分析,查明断裂的形成与发展,确定断裂构造及断块间的相互作用方式[15].采用应力测量、数值分析、3S集成技术、无人机航拍与航测等手段,确定区域地质构造形式、构造背景、岩体应力状态等,为人类的工程活动提供地质环境信息,预测工程活动可能产生的地质动力效应[16].

基于地质动力区划法,遵循整体到局部的原则,在比例尺1∶2 500 000～1∶10 000的地形图上,依次划分鹤岗南部矿区和东荣矿区的Ⅰ～Ⅴ级断裂构造,确定富力矿、兴安矿、峻德矿、东荣一矿、东荣二矿、东荣三矿等6个矿井的Ⅴ级断块图,分别形成鹤岗南部矿区断裂构造(图2)和东荣矿区断裂构造(图3).

图3 东荣矿区断裂构造及分区

2 矿区断裂分形几何分析

2.1 分形几何计算方法

分形维数有不同的定义和计算方法.分形的对象决定分形维数的计算方法,作为线状的断裂构造主要采用网格法来计算分形维数.网格法是通过改变研究尺度来确定,采用大小、形状相同的正方形网格覆盖研究区断裂构造分布图,统计计算在不同计算尺度下断裂覆盖网格数目.假设计算网格尺度为r,统计网格数目为N(r).大量研究结果表明,网格尺度r和网格数目N(r)满足指数关系:

N(r)=C1r-D1.

(1)

如果将网格尺度r和网格数目N(r)的统计数据拟合在双对数坐标系中,拟合曲线为一条直线,则满足线性回归方程:

lnN(r)=-D2lnr+C2.

(2)

式中:C1,C2为常数;D1,D2为断裂分形维数.

以东荣矿区为例,将断裂构造图划分为47个分区,每个分区尺度为2 km×2 km(如图3所示).在每个分区中,采取3个研究标度,分别以1 km×1 km,0.5 km×0.5 km和0.25 km×0.25 km的尺寸网格去覆盖每个分区,并统计各分区断裂的N(r)值,拟合出lnr与lnN(r)之间的线性回归曲线,得到各分区断裂的分形维数D和相关系数R2.鹤岗南部矿区的分形几何方法与东荣矿区类似,鹤岗南部矿区断裂构造图划分为28个分区.

2.2 鹤岗南部矿区断裂分形几何特征

建立不同尺度网格覆盖鹤岗南部矿区断裂构造图,计算断裂分形维数.鹤岗南部矿区各矿井断裂分形维数线性回归图如图4所示.由图4可知:富力矿断裂分形维数为1.680 5,相关系数为0.990 5;兴安矿断裂分形维数为1.631 7,相关系数0.989 2;峻德矿断裂分形维数为1.552 9,相关系数为0.991 9.这3个矿井断裂线性相关系数均接近1,说明在0.25～2.00 km分形尺度下,断裂具有较好的空间几何结构和自相似性特征.

图4 鹤岗南部矿区各矿井断裂分形维数线性回归曲线

鹤岗南部矿区各矿井分区分形维数对比数据如表1所示.覆盖富力矿的7个分区的分形维数全部高于1.20,介于1.20和1.65之间,这说明该矿内断裂分布不均,具有明显差异性;7,8,11这3个分区的分形维数均高于1.55,说明这些分区的区域断裂构造较为发育,其复杂程度也较高,大部分为NW向断裂.

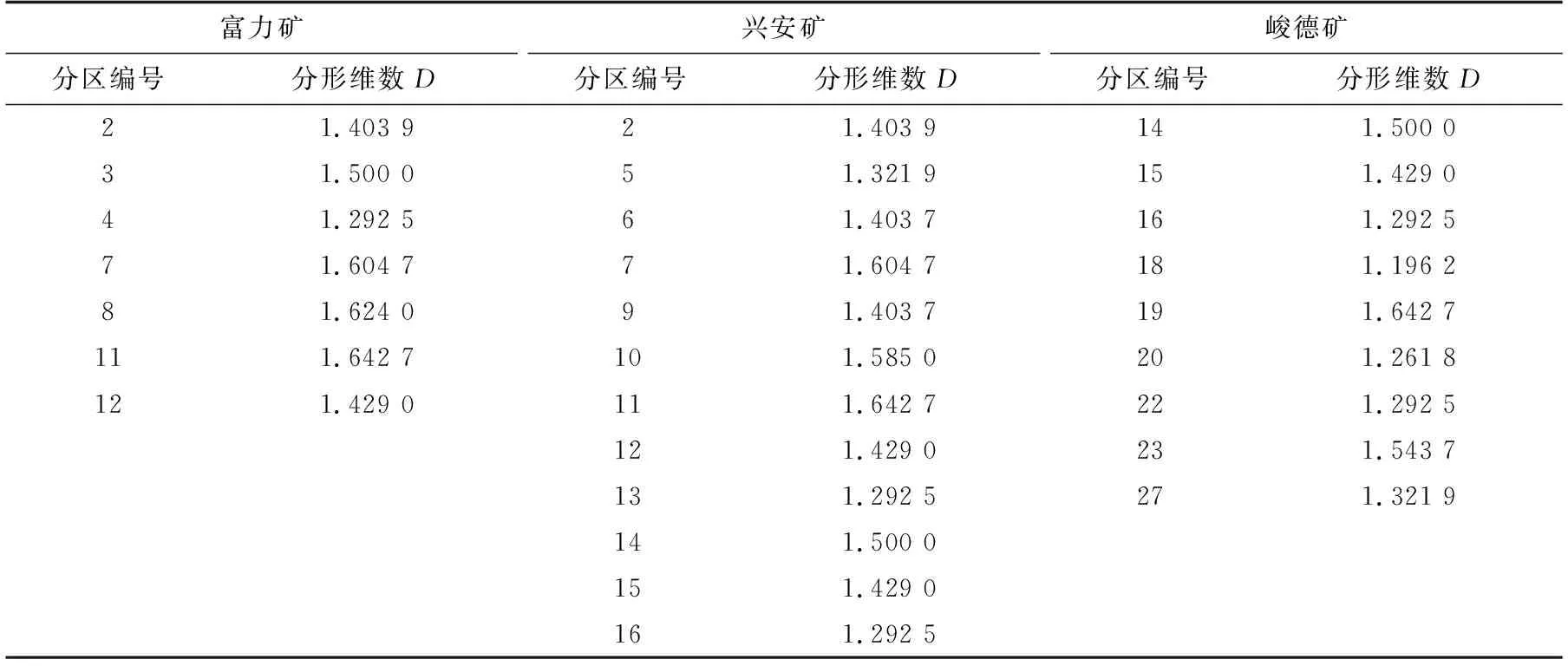
表1 鹤岗南部矿区各矿井分区分形维数对比

兴安矿的12个分区的分形维数均大于1.20,数值在1.20～1.65,差异较大,说明该矿断裂多处发育,但分布不均;7,10,11这3个分区的分形维数全部大于1.55,说明这些区域断裂较为发育,复杂程度较高,大多为NW向断裂和近SN向断裂.

覆盖峻德矿的9个分区的分形维数均大于1.00,数值介于1.00和1.65之间,说明该矿断裂分布不均,各分区断裂分布差异性明显;只有19分区的分形维数高于1.55,说明这一区域断裂密集程度高,发育较好,复杂程度也较高.

2.3 东荣矿区断裂分形几何特征

东荣矿区各矿井断裂分形维数线性回归图如图5所示.由图5可知:东荣矿区3个矿的断裂分形维数分别为1.526 8,1.465 9,1.384 9;线性相关系数分别为0.991 6,0.989 2,0.991 6,直线的拟合程度较高,说明矿井具有较好的分形几何结构特征和统计自相似性.

图5 东荣矿区各矿井断裂分形维数线性回归曲线

东荣矿区各矿井分区分形维数对比数据见表2.对东荣一矿有控制作用的9个分区的分形维数全部高于0.7,介于0.7和1.6之间,这说明该矿内断裂分布不均,各分区断裂分布有明显差异性;只有39分区的分形维数高于1.526 8,说明39分区的断裂构造较为发育,其复杂程度也较高,大部分为NW向断裂.

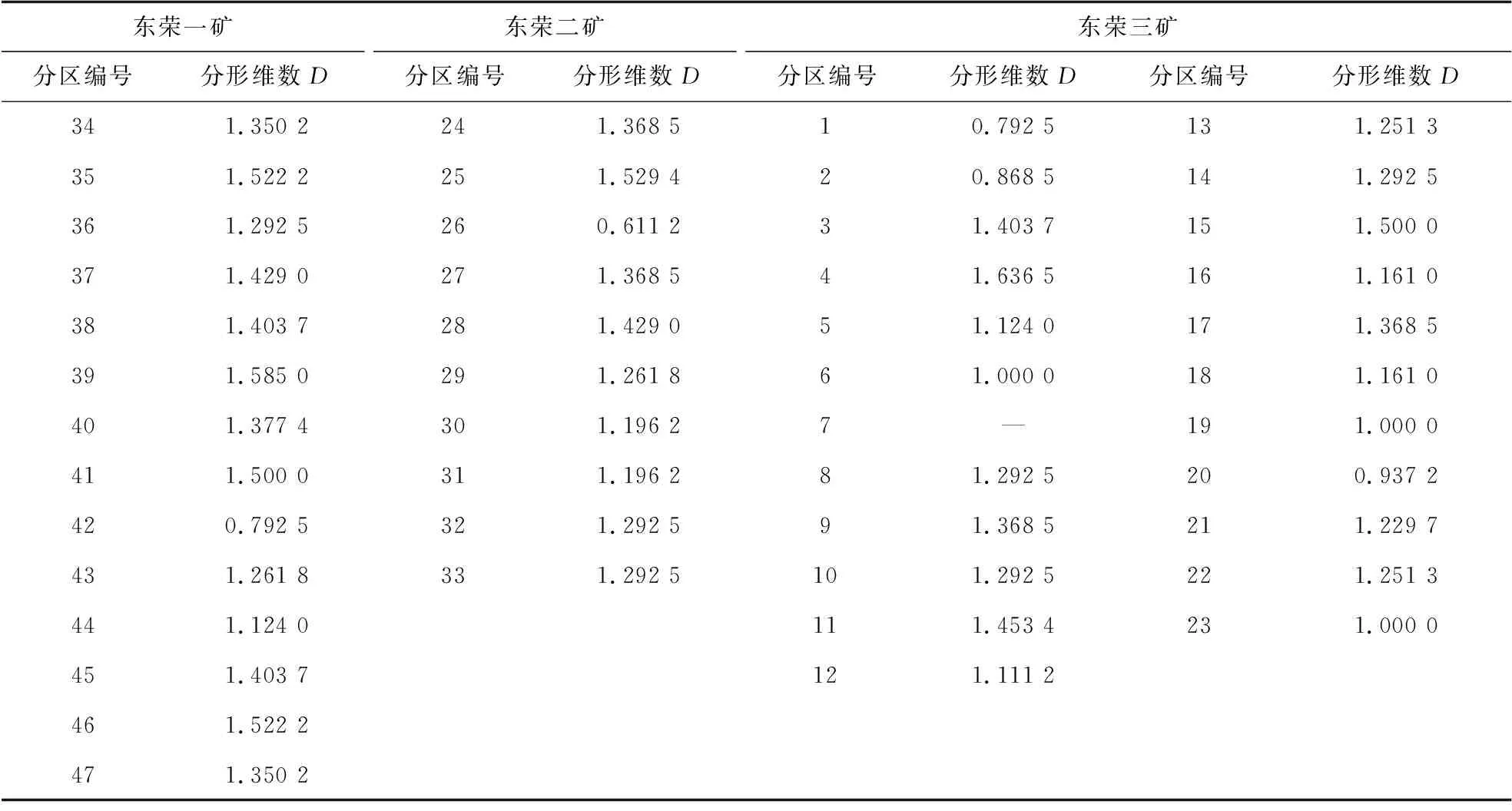
表2 东荣矿区各矿井分区分形维数对比

对东荣二矿有控制作用的8个分区的分形维数均大于0.6,数值在0.6～1.6,差异较大,说明该矿断裂多处发育,但分布不均;只有25分区的分形维数大于1.465 9,说明25分区断裂较为发育,复杂程度较高.

对东荣三矿有控制作用的15个分区的分形维数均大于0.8,数值介于0.8和1.7之间,说明该矿断裂分布不均,各分区断裂分布差异性明显;其中3,4,11,15这4个分区的分形维数高于1.384 9,说明这4个分区断裂密集程度高,发育较好,复杂程度也较高.

3 断裂分形维数与冲击地压相关性分析

鹤岗南部矿区共发生冲击地压46次,其中富力矿发生冲击地压8次,位于多采区、多工作面;兴安矿发生冲击地压12次,位于多采区、多工作面;峻德矿发生冲击地压26次,位于一采区、多工作面.东荣矿区共发生冲击地压14次,均位于东荣三矿一采区、一个工作面.

鹤岗南部矿区和东荣矿区断裂分形维数线性回归图分别如图6和图7所示.从矿区的角度分析,在分区标度为2 km时,鹤岗南部矿区的分形维数为1.552 8,东荣矿区的分形维数为1.448 5,鹤岗南部矿区的分形维数大于东荣矿区的分形维数,冲击地压发生次数也是如此.这说明矿区断裂分形维数与冲击地压发生次数有较好的相关性,断裂分形维数越大,冲击地压发生的可能性也越大.

图6 鹤岗南部矿区断裂分形维数线性回归曲线

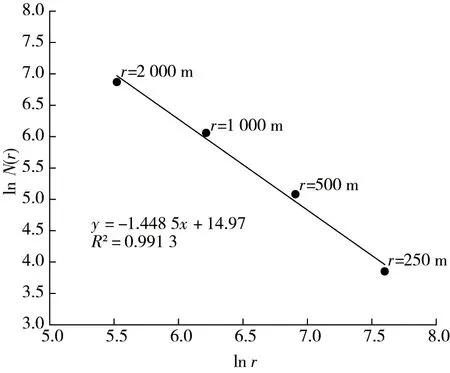
图7 东荣矿区断裂分形维数线性回归曲线

从矿井的角度分析,富力矿分形维数>兴安矿分形维数>峻德矿分形维数>东荣三矿分形维数,而冲击地压发生次数由高到低依次为峻德矿、东荣三矿、兴安矿、富力矿,由此看出矿井断裂分形维数与冲击地压发生次数没有较好的一致性.但是分析各个矿井冲击地压发生位置可以发现,冲击地压有聚集性发生的特点.因此,可以建立冲击地压发生位置与断裂分区分形维数的联系.

鹤岗南部矿区各矿井断裂分形维数如图8所示.富力矿发生冲击地压的位置均位于7分区且分散分布,断裂分区分形维数为1.604 7,高于该矿井大部分分区分形维数,且与矿井断裂分形维数相近;兴安矿发生冲击地压的位置大部分位于11分区且分布较分散,断裂分区分形维数为1.642 7,大于该矿井所有分区的分形维数,且大于矿井断裂分形维数;峻德矿发生冲击地压的位置均位于15分区且分布集中,断裂分区分形维数为1.429 0,与矿井断裂分形维数相近.

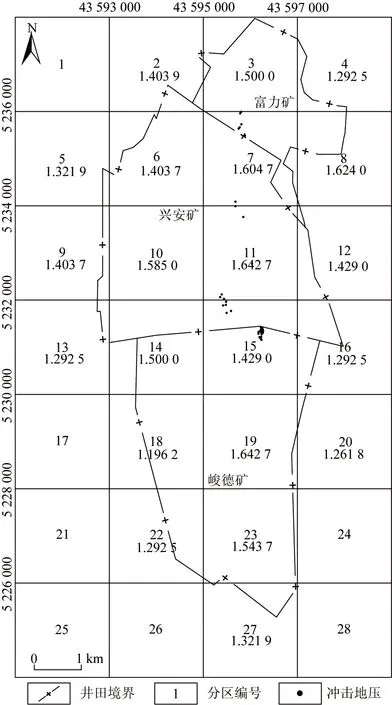
图8 鹤岗南部矿区各矿井断裂分形维数

东荣矿区各矿井断裂分形维数如图9所示.东荣三矿冲击地压发生的位置均位于10分区且分布集中,断裂分形维数为1.292 5,高于该矿井大部分分区分形维数,且与该矿井断裂分形维数相近.从上述分析可知,断裂分区分形维数与冲击地压空间位置有较强的耦合关系,断裂分形维数较大,则冲击地压分散分布;反之,断裂分形维数较小,则冲击地压集中分布.

图9 东荣矿区各矿井断裂分形维数

4 结论

1)在一定分形尺度下,断裂构造具有很好的统计自相似性.

2)不同矿区的断裂构造分形特征具有明显差异,同一矿区下不同矿井的断裂构造分形特征亦是如此.

3)断裂分形维数与冲击地压分布位置和发生次数有较强的相关性,且分区分形维数越大,断裂复杂程度及发育程度亦越高.