基于模糊可靠度的缓和曲线最小长度计算方法研究

朱 福,陈 亚,陈文怡

(吉林建筑大学 交通科学与工程学院，吉林 长春 130118)

0 引言

道路线形设计需满足汽车行驶特性要求，才能保证行车的安全性与舒适性。车辆在平曲线路段行驶时，离心力影响了行车的安全性与舒适性，除需解决横向滑移与倾覆问题外，还需解决横向力的过渡渐变问题[1]。道路线形设计中通过设置缓和曲线使曲率逐渐变化，解决横向力的过渡渐变问题，达到提高行车舒适性的目的。缓和曲线是设置在直线与圆曲线之间或半径相差较大的两个转向相同的圆曲线之间的一种曲率连续变化的曲线[1]。王福建等[2]分析了大量的交通事故，发现不合理的缓和曲线长度影响驾驶员的驾驶行为和行车安全。张合沛等[3]、BRUSTAD等[4]、蒋启平[5]考虑车辆的运行速度及载重对缓和曲线的影响，通过改进缓和曲线的算法使缓和曲线更贴合实际。PAN[6]提出k型曲线，它是一种新的缓和曲线形式，在相同的连接条件下，该曲线的长度要大于回旋线。李诗佳等[7]、胡昌亮等[8]对隧道洞口处和圆曲线半径大于不设超高最小半径条件下设置缓和曲线的必要性进行了讨论分析。富志鹏等[9]、任春宁等[10]对中间带宽度变化分幅过渡方式进行分析，分别给出用三次抛物线替代线性渐变过渡和调整缓和曲线参数两种不同的处理方式。屈强等[11]、杨春雷等[12]采用仿真技术对不同工况进行模拟，对缓和曲线段的排水和行车安全等进行了分析。

目前，学者们[2-12]主要开展了缓和曲线长度对交通安全影响的研究，分析了缓和曲线的布设形式，探讨了缓和曲线路段中间带宽度与排水等问题，而关于缓和曲线最小长度计算方法的适用范围还未见有人涉猎。已有研究表明[13]，公路线形设计参数存在随机性与模糊性。但当前学者们仅基于可靠度理论开展了公路工程结构或线形的设计参数可靠性分析[14～19]，关于公路线形设计参数的模糊可靠性分析还属空白。缓和曲线最小长度的影响因素具有不确定性，且因素之间关系错综复杂，需要用不确定性理论和方法进行分析，为此引入可靠性来确定缓和曲线长度。本文在分析缓和曲线最小长度计算方法适用范围的基础上，以可靠度理论与模糊数学理论为基础，建立了缓和曲线最小长度模糊可靠度功能函数，推导了缓和曲线最小长度的模糊可靠度求解公式，并通过案例进行了验证。考虑缓和曲线长度影响因素的模糊性，将模糊可靠度理论应用于缓和曲线最小长度计算，对提高缓和曲线最小长度可靠度计算精度具有重要意义，可为公路线形设计提供理论依据。

1 缓和曲线最小长度计算方法

1.1 按乘客感觉舒适所需最小长度

缓和曲线上曲率逐渐变化，导致在缓和曲线上行驶车辆的离心加速度逐渐变化，若缓和曲线过短，离心加速度变化快，会让人感觉到一股横向冲击力。依据离心加速度变化率给出使乘客感觉舒适的缓和曲线最小长度计算方法[1]。假设车辆在缓和曲线段行驶所用的时间为t，车辆运行速度为v，则离心力产生的离心加速度表示为：a=v2/r。由图1可知，车辆从缓和曲线起点到达缓和曲线终点，曲率半径r由∞均匀地变化到R，离心加速度由0均匀地增加到v2/R，离心加速度的变化率为：

(1)

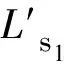
(2)

1.2 按超高渐变率所需最小长度

依据超高计算公式ih=v2/127R-μ可知，运行速度一定时，超高随曲率的变化而变化。因此，缓和曲线段超高值是逐渐变化的，该超高值变化范围内的长度为超高过渡段，在超高过渡段内超高值的变化称为超高渐变率。若超高过渡段太短，路面从双面坡突变到单面坡，会对车辆行驶不利且影响公路线形美观；若超高过渡段太长，导致超高渐变率太小，则会使公路排水不畅[1]。本文只考虑缓和曲线段与超高过渡段相等情形下，选择适中的超高渐变率，根据规范[20]给出的最小超高过渡段长度Ls见式(3):

(3)

(4)

1.3 按行驶时间所需最小长度

(5)

通过分析3种缓和曲线最小长度的计算公式可以得出以下结论:

a.与按行驶时间所需最小长度相比,按乘客感觉舒适所需最小长度与按超高渐变率所需最小长度考虑了圆曲线半径对缓和曲线的影响。

b.按乘客感觉舒适所需最小长度与按超高渐变率所需最小长度均涉及到车辆在缓和曲线段的行驶时间,前者是以行驶时间为桥梁,将离心加速度变化率与缓和曲线最小长度联系起来,后者直接取行驶时间为定值。

c.当运行速度为唯一变量时,按行驶时间所需最小长度、按乘客感觉舒适所需最小长度和按超高渐变率所需最小长度计算的缓和曲线最小长度分别是运行速度的一次函数,二次函数和三次函数,如图2所示。

图2 3种计算公式对比

由图2可知,在不同运行速度条件下,3种公式计算出的缓和曲线最小长度具有明显的差异性。当运行速度位于区间(0,v1)时,按超高渐变率所需最小长度为负值,显然,此时不具有实际意义;当运行速度位于区间(v1,v2)时,缓和曲线最小长度大小关系为:按行驶时间所需最小长度>按乘客感觉舒适所需最小长度>按超高渐变率所需最小长度;当运行速度位于区间(v2,v3)时,缓和曲线最小长度大小关系为:按行驶时间所需最小长度>按超高渐变率所需最小长度>按乘客感觉舒适所需最小长度;当运行速度位于区间(v3,v4)时,缓和曲线最小长度大小关系为:按超高渐变率所需最小长度>按行驶时间所需最小长度>按乘客感觉舒适所需最小长度。由此可见,3种计算公式具有一定的适用范围。

2 缓和曲线最小长度模糊可靠性分析方法

结构可靠性是指结构在规定时间内和规定条件下完成预定功能的能力，并将结构在规定时间内和规定条件下完成预定功能的概率称为可靠度[21]。所谓缓和曲线最小长度模糊可靠性是指在考虑运行速度具有模糊性和随机性的条件下，缓和曲线最小长度在规定时间内和规定条件下完成预定功能的能力。缓和曲线最小长度模糊可靠性分析方法就是从概率的角度分析缓和曲线最小长度安全与失效的可能性大小。若缓和曲线最小长度超过某一数值，不能满足设计规定的功能要求，则在该数值下的状态称为极限状态。该状态是缓和曲线最小长度是否可靠的临界状态，超过这一状态时，缓和曲线最小长度不能完成预定功能。不能完成预定功能的概率，称为失效概率。

2.1 缓和曲线最小长度模糊可靠度功能函数建立

假设模糊功能函数为：

Z=C-E

(6)

式中：C为公路提供设计参数常量；E为驾驶员期望设计参数模糊变量。显然，C和E相互独立。

根据式(6)可以得出极限状态方程为：

Z=C-E=0

(7)

当Z>0时，该路线设计参数满足设计要求；当Z=0时，该路线设计参数处于临界值；当Z<0时，该路线设计参数不满足设计要求，处于失效状态。

根据式(2)、式(4)和式(5)，得出缓和曲线最小长度的模糊可靠度功能函数如表1所示。

表1 3种计算公式的功能函数

2.2 缓和曲线最小长度模糊可靠度求解

(8)

式(8)中的参数可由以下公式[23]进行计算:

(9)

m=∂

(10)

ο=∂+2(ρ-∂)

(11)

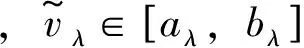
图3 模糊变量的λ-截集

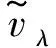
(12)

(13)

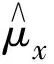
(14)

(15)

Z′i=kiv+bi(i=1,2,3)

(16)

式中：ki为功能函数一次项系数；bi为常数项。

由于功能函数Z′i是v的线性函数，根据概率论中均值和方差的性质，可以得出：

(17)

(18)

缓和曲线最小长度的可靠度通常用可靠指标β和失效概率Pf来表示，两者的关系如图4所示。

图4 可靠指标与失效概率关系

由图4可见，缓和曲线最小长度的可靠指标可以用均值μZ和标准差σZ的比值来表示，即：

(19)

缓和曲线最小长度的失效概率Pf可以表示为:

Pf=1-Φ(β)

(20)

其中，Φ表示标准正态分布函数。该表达式表明，若已知可靠指标的值，则可以确定缓和曲线最小长度的失效概率，并可以用来评价缓和曲线最小长度的可靠性。

3 工程案例与结果分析

3.1 工程案例

某高速公路是中国早期建设的联结南北交通的主动脉，于上世纪 90年代全线通车运营。选取的工程路段(K115～K287)建成时为双向四车道，沥青混凝土路面，设计速度为120 km/h，发生事故路段的运行速度数据[24]，如表2所示。

表2 运行速度统计数据

根据三角模糊数计算参数的定义，分别选取表2中的最大值ρ=124.21 km/h，中间值∂=(118.41+118.01/2)km/h=118.21 km/h和最小值θ=107.47 km/h。将其代入式(9)～式(11)，计算出运行速度的三角隶属函数。如下：

(21)

根据范李等[25]对弯道道路的测试,得出横向力系数同运行速度的关系式如下:

μ=0.25-0.204×10-2v+0.63×10-5v2

(22)

根据规范可得,缓和曲线最小长度参考值C的取值为100 m。若超高旋转轴位于道路内边线,超高渐变率的取值为1/200,旋转轴至行车道外侧边缘的宽度取值为15 m。为使求解过程简化,离心加速度取值为0.55 m/s3。将运行速度为115.84 km/h代入式(22),可以得出μ的取值为0.1,分别求出圆曲线半径取值为650 m与1 000 m条件下3种缓和曲线最小长度的简化后功能函数,如表3所示。

表3 3种停车视距模型的简化功能函数

将当量均值和标准差代入式(17)和式(18)，分别计算圆曲线半径为650 m与1 000 m缓和曲线最小长度的可靠指标和失效概率。其计算结果如表4。

表4 缓和曲线最小长度可靠指标与失效概率

3.2 结果分析

圆曲线半径取值为650 m和1 000 m条件下，缓和曲线最小长度的模糊可靠度失效概率与传统可靠度失效概率的计算结果，见图5。由图5可知，按乘客感觉舒适所需最小长度在圆曲线半径为1 000 m时，模糊可靠度失效概率趋近于0%，说明该公式计算出的缓和曲线最小长度远小于规范规定值，其计算结果不合理。与传统可靠度相比较，模糊可靠度的失效概率小，由此可知，模糊可靠度计算方法比传统可靠度计算精度更高。按超高渐变率所需最小长度在圆曲线半径为650 m时，失效概率达到了99%，并且与模糊可靠度相比，传统可靠度的失效概率更小，说明在采取圆曲线半径极限值时，缓和曲线最小长度达不到超高过渡段最小长度的要求，其计算方法失去实际意义。

(a)R=650 mm时

由于按行驶时间所需最小长度计算过程中不涉及圆曲线半径，仅讨论按乘客感觉舒适所需最小长度和按超高渐变率所需最小长度在不同圆曲线半径条件下，运用模糊可靠度理论计算得到的可靠指标与失效概率的变化规律，见图6。

(a)可靠指标

由图6可知，按乘客感觉舒适所需最小长度与按超高渐变率所需最小长度的可靠指标和失效概率变化区间所对应的圆曲线半径不同，按乘客感觉舒适所需最小长度的可靠指标和失效概率在圆曲线半径为500～750 m的范围内变化明显，按超高渐变率所需最小长度的可靠指标和失效概率在圆曲线半径为750～1 000 m的范围内变化明显。由此可知，在计算缓和曲线最小长度时，若圆曲线半径的取值小，选用按乘客感觉舒适所需最小长度计算公式计算结果更精确，若圆曲线半径的取值大，选用按超高渐变率所需最小长度计算公式计算结果更精确。

上述分析表明，不同的圆曲线半径计算出的失效概存在差异，说明圆曲线半径对缓和曲线最小长度存在一定的影响，然而，我国规范采用按行驶时间所需最小长度计算公式给出的缓和曲线最小长度规定值，忽略了圆曲线半径对缓和曲线最小长度的影响。鉴于我国在公路线形方面没有相关的可靠度统一规范，依据公路工程结构可靠度设计统一标准[26]中对公路安全等级的相关规定，根据模糊可靠度计算方法计算出缓和曲线最小长度失效概率为5%时，运行速度为120 km/h的不同圆曲线最小半径的缓和曲线最小长度推荐值，如表5所示。

表5 不同圆曲线半径条件下缓和曲线最小长度的推荐值

与规范中的缓和曲线长度相比，给出的推荐值考虑了圆曲线半径对缓和曲线的影响，使缓和曲线长度取值更加具体，可提高了车辆在行驶中的安全性。

4 结论

本文详细分析了缓和曲线的研究现状，在考虑缓和曲线最小长度影响因素的随机性与模糊性基础上，推导出了缓和曲线最小长度模糊可靠度计算方法，并通过案例分析对比，得出如下结论：

a.与传统缓和曲线最小长度可靠度计算方法相比，基于模糊可靠度理论推导的缓和曲线最小长度可靠度计算方法得出的可靠指标高，失效概率小，精度更高。

b.将按乘客感觉舒适所需最小长度与按超高渐变率所需最小长度用于缓和曲线最小长度模糊可靠性分析时，按乘客感觉舒适所需最小长度计算公式适用于圆曲线半径较小的工况，按超高渐变率所需最小长度计算公式适用于圆曲线半径较大的工况。

c.规范采用按行驶时间所需最小长度计算公式计算出的缓和曲线最小长度忽略了圆曲线半径的影响，其规定的取值有待商榷。依据按乘客感觉舒适所需最小长度和按超高渐变率所需最小长度的计算公式给出的缓和曲线最小长度推荐值，可使公路线形设计更为安全可靠。