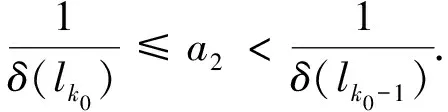Relationships between ΛφBV and BV(q,δ)*
2023-11-08GEAjunWANGHepingYANDunyan
GE Ajun, WANG Heping, YAN Dunyan
(1 School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China;2 School of Mathematical Sciences, Capital Normal University, Beijing 100048, China)(Received 24 November 2021; Revised 8 April 2022)
Abstract In this note, we obtain the sufficient and necessary conditions for the inclusions ΛφBV⊂BV(q,δ), and BV(q,δ)⊂ΛφBV is false when φ satisfies the Δ2 condition.
Keywords Λφ-bounded variation; generalized Wiener class; embedding


where the supremum is taken over all sequences={Ik}={[ak,bk]} of non-overlapping intervals in [0,1],f(Ik)=f(bk)-f(ak).We sayf∈ΛφBVif there exists a constantc>0 such thatVΛφ(f/c)<∞.It is easy to see thatΛφBVis a linear space. The linear spaceΛφBVis a Banach space, which endowed with the norm
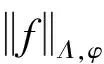
We say thatφsatisfies the condition Δ2if there exista>0 andδ>0 such thatφ(2x)≤δφ(x) for allx∈(0,a].Musielak and Orlicz[1]considered thatΛφBV={f|VΛφ(f)<∞} if and only ifφsatisfies the condition Δ2.
The classΛφBVwas first introduced by Schramm and Waterman[2]in 1982. In the caseφ(x)=xp(p≥1),fis said to be of boundedp-Λ-variation function. The corresponding classΛBV(p)was introduced in 1980 by Shiba and called by the Waterman-Shiba class. Ifp=1,fis said to be ofΛ-bounded variation, and we denotef∈ΛBV.The corresponding class is the well-known Waterman classΛBV.In the caseΛ={1}, we get the classBVφofφ-bounded variation. More specifically, whenφ(x)=xp(p≥1), we get the classBVpwhich is called the Wiener class. The classBV1is the well known class of bounded variationBV.
It is easily seen from the definition thatΛφBVfunctions are bounded, and the discontinuities of aΛφBVfunction are simple and, therefore, at most denumerable. From Refs. [3-8], we know the classΛφBVhad been studied mainly because of their applicability to the theory of Fourier series and some good approximative properties.
Kita and Yoneda[9]introduced a new function space which is a generalization of Wiener classes (see also Refs. [10-11]). The concept was further extended by Akhobadze[12]who studied many properties of the generalized Wiener classesBV(q,δ) thoroughly (see Ref. [13]) .
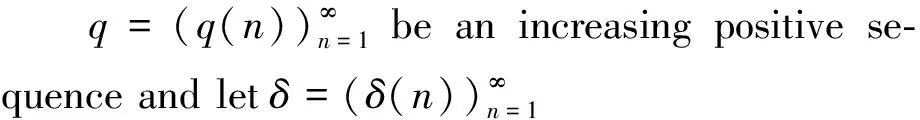


The following result was obtained by Hormozi et al.[15]: forp∈[1,∞),qandδsequence satisfying the conditions in Definition 1.1, the inclusionΛBV(p)⊂BV(q,δ) holds if and only if
In this paper, we extend the results above and obtain the corresponding inclusions ofΛφBVandBV(q,δ).Our main results can be formulated as follows.
Theorem1.1Forqandδsatisfying the conditions in Definition 1.1, the inclusionΛφBV⊂BV(q,δ) holds if and only if
(1)
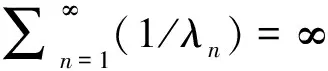
ProofofTheorem1.1
SufficiencySuppose that (1) holds. Letf∈ΛφBV.It suffice to showf∈BV(q,δ).We will prove the inequality
V(f,q,δ)
(2)

LetAbe a positive constant,s∈N,1≤q<∞,0≤xs≤…≤x2≤x1, and

It follows from Wang[16]that
whereφ-1is the inverse function ofφ.We note that

NecessitySuppose (1) does not hold. Then there is an increasing sequence {nk} of positive integers such that for all indicesk
δ(nk)≥2k+2,
(3)
and
(4)
We will construct a functiongsuch thatg∈ΛφBVandg∉BV(q,δ).Let {mk} be a sequence of positive integers such that
1≤mk≤δ(nk),
(5)
and
(6)
Set

Consider
gk(y)

where
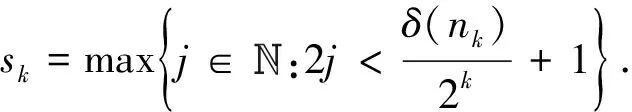
It follows from the definition ofskthat
(7)
By (7) and (3), we have
(8)
IfNk=mk, then
and ifNk=sk, then by (8) and (5) we have
Hence, for allk,
(9)
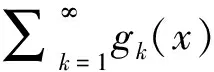
which impliesg∈ΛφBV.
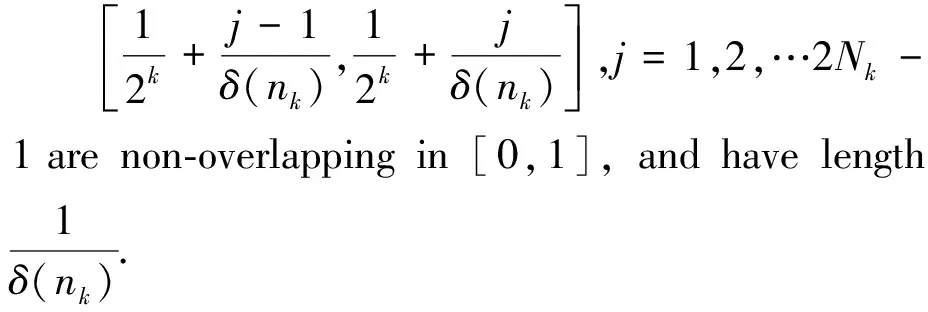

where in the second inequality, we used (9), in the third inequality we used (4) and (6). Sincekwas arbitrary,V(g,q,δ)=∞ which shows thatg∉BV(q,δ).This completes the proof of the necessity.
Theorem 1.1 is proved.
□
ProofofTheorem1.2
We choose a strictly increasing sequence {lk:k≥1} of positive integers such thatl1=1 and
q(lk)≥ln(k+1) for allk≥2.
Set
f(x)
where
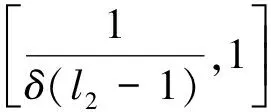
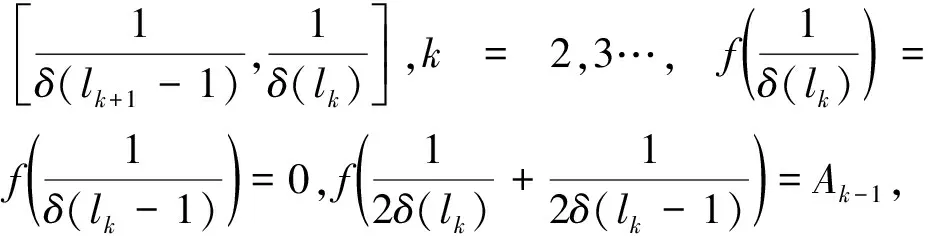
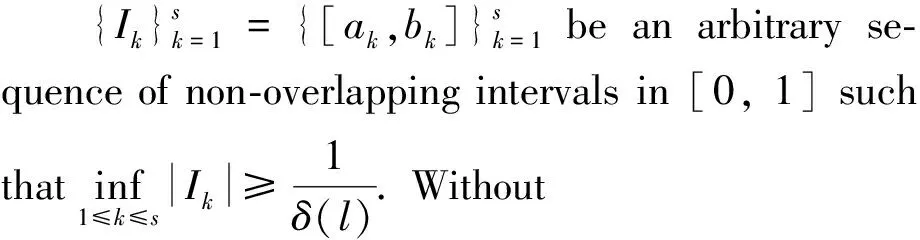
0≤a1 Then |f(b1)-f(a1)|≤Ak0. We also note that {Ak} is non-increasing and It then follows that This impliesf∈BV(q,δ). Next, we show thatf∉ΛφBV.Sinceφsatisfies the condition Δ2, it suffices to prove that VΛφ(f)=∞. We have VΛφ(f) which impliesf∉ΛφBV.The proof of Theorem 1.2 is complete. □