基于梯度提升决策树算法的膨润土膨胀力预测

2023-11-08王琼张佳南高岑苏薇刘樟荣叶为民

世界核地质科学 2023年3期

王琼，张佳南，高岑，苏薇，刘樟荣，叶为民

（同济大学岩土及地下工程教育部重点实验室，上海 200092）

随着经济的迅速发展，能源需求快速增加，高效、清洁的核能在全球能源转型中发挥着越来越重要的作用。然而，核能发电不可避免地会产生放射性强、毒性大、半衰期长的高放射性废物（高放废物）［1］。研究表明：深地质处置是其最为可行可靠的处理方法，即把高放废物埋在距离地表约500～1 000 m 的稳定地质体中，通过设置多重屏障（天然屏障、工程屏障、废物罐）使其与人类生存环境永久隔离［2］。其中，作为工程屏障的缓冲/回填材料需具备水力学屏障、核素阻滞屏障、传导和散失放射性废物衰变热等重要功能［3］。高压实膨润土，由于具有低渗透性、高膨胀性、高阳离子交换能力和较高的核素阻滞能力，目前已被选为高放废物处置库工程屏障的首选材料。

实际工程中，一方面要求缓冲/回填材料的高膨胀能力使施工接缝自封闭，另一方面又要求膨胀力不高于处置库围岩的最小主应力以防止对母岩的侵扰和破坏。因此，膨润土的膨胀性能是评价其缓冲性能的关键指标之一。

国内、外已有众多关于高压实膨润土膨胀力、膨胀变形特性及其影响因素的研究成果。膨润土的膨胀特性依赖于蒙脱石含量和初始条件（干密度和含水量）。不同类型膨润土因其蒙脱石含量不同而具有不同的膨胀性能，蒙脱石含量越高则膨胀力越大［4-5］。膨润土的干密度、含水率（反映吸力）等初始条件会影响其结构，从而在影响膨润土膨胀能力方面表现得尤为重要。干密度越大膨胀力越大［6-9］；而初始含水量对最终膨胀力的影响不明显［10］。此外，在缓冲材料性能改良的研究中发现，纯膨润土中加入砂/岩屑等添加剂时，混合材料的骨架成分会随添加剂掺入率而变化，从而对膨胀力产生影响，表现为混合材料的膨胀性能会随添加剂含量增加而减弱［11］。

事实上，由于膨润土在深地质处置库中作为工程屏障而发挥缓冲/回填作用，故除上述土体本身特性之外，处置库所处耦合环境中各因素也显著影响膨润土的膨胀性能。工程屏障会直接接触到废物罐以传导/散失高放废物衰变热，温度的变化会使膨润土中的水分迁移、脱离并影响膨润土自身结构［12-13］，从而影响其膨胀力［14-16］。并且，膨润土具有较大的离子交换容量，处置库中的高压实膨润土砌块长期受到含盐地下水的化学作用，处置库运营过程中水泥水解造成的碱性环境也易将膨润土中的蒙脱石溶解［17］，因而环境中溶液类型及浓度也是影响其膨胀力的重要因素［18］，膨润土的膨胀力会随溶液浓度的增加而相应减小［19-20］。

综上可知，在实际处置环境中，膨润土膨胀性能的影响因素较多、作用机制复杂，且目前对综合考虑多种因素影响的相关研究尚少，使得处置库耦合环境下膨润土膨胀性能的快速准确预测成为难点。

近年兴起的机器学习方法是数据分析、预测的有效手段，对上述所提出的问题具有很高适用性。在地质工程领域，已有许多学者运用机器学习来研究存在较多影响因素的课题。尤其是机器学习中的梯度提升算法，在多因素影响下的分类、回归问题方面表现优异，常被用于地质体识别［21-22］、成矿预测［23］和地质灾害预测［24］等课题的研究，且能够获得较为准确的预测结果，与本文的研究目标有较强的契合性。

因此，本文采用泛化能力出众的梯度提升决策树（GBDT）算法，通过梳理和总结国内外相关的实验研究成果，以目前世界上较为典型的膨润土为研究对象，选取干密度、含水率、添加剂类型及掺入比、溶液成分及浓度为特征参数，构建了基于GBDT 回归算法的膨润土膨胀力预测模型，以期为我国已经开建的地下实验室现场试验与处置库建设提供设计参数与理论支撑。

1 理论分析

1.1 膨润土的膨胀机理

膨润土是以蒙脱石为主要成分的黏性土，通常含有少量伊利石、高岭石、石英、方解石和长石等矿物。蒙脱石是黏土矿物中最具膨胀性的一类，因此膨润土的膨胀性能与蒙脱石的特性密切相关。蒙脱石是2：1 型层状硅酸盐矿物，由上、下两片硅氧四面体和中间一片铝（镁）氧（羟基）八面体构成，晶体构造如图1 所示。

图1 蒙脱石晶体构造示意图Fig.1 Schematic diagram of the crystal structure of montmorillonite.

膨润土的膨胀包括两个部分，即：晶层膨胀和双电层膨胀。蒙脱石中的硅氧四面体和铝氧八面体中的Si4+和Al3+常被低价阳离子置换，使晶层间产生多余的负电荷，因此晶层间会吸附大半径阳离子（如K+、Na+和Ca2+等）以保持整体的电中性。这些大半径阳离子通常以水化状态存在，可相互交换，因此蒙脱石具有较高的离子交换容量与吸水能力，在遇水时水分子易沿硅氧四面体层进入晶层间，使得晶层间距扩大，宏观上即表现为体积膨胀。另一方面，孔隙中的水与黏土颗粒表面接触时会受到颗粒表面双电层（图2）的电场作用，极性水分子被吸附于土粒周围形成一层结合水膜。当极性水分子不断被吸附、结合水膜逐渐增厚，黏土颗粒即被楔开，颗粒间距增大，导致宏观上的体积膨胀，即双电层膨胀。

图2 双电层结构示意图Fig.2 Schematic diagram of double electric layer structure

1.2 膨润土膨胀力的主要影响因素

膨胀力是指膨胀性土遇水而保持土体积不变所需要的压力［5］。作为膨润土主要矿物成分的蒙脱石晶体结构特殊，使得膨润土具有极其复杂的构造层次——孔隙层次多、形状大小各异，而膨润土吸湿膨胀的性能很大程度上取决于它的孔隙结构，因此，影响膨润土孔隙的因素也会相应地影响到膨润土的膨胀性能。

膨润土的自身性质是决定其孔隙结构的根本因素，可视为内因，包括蒙脱石含量、干密度和含水量等初始条件、膨润土中的添加剂类型和掺入率。并且，高压实膨润土砌块是在处置库中发挥其缓冲/回填作用，故处置库的环境因素对其孔隙结构造成的影响也不容忽视，视为外因，包括环境温度、盐/碱溶液及其浓度。

综上所述，内因和外因都将通过影响膨润土的结构而对其膨胀力造成一定影响。

1.3 GBDT 算法原理

决策树算法（Decision Tree）是机器学习中的一种典型算法，可以解决分类问题与回归分析，是常用的数据预测模型，应用十分广泛。其中，决策树是一种较弱的基学习器，其单棵树预测的准确性比传统分类与回归方法弱，但可通过集成学习的方法将基学习器组合，从而提升决策树的预测效果。 GBDT（Gradient Boosting Decision Tree）便是一种基于集成学习（Ensemble Learning）策略的决策树算法，它由多棵CART 回归决策树组成，通过将所有树的结果相加得出最终结论。

GBDT 提升树采用前向分步算法，基学习器为回归树fm(x)。首先初始化回归树f0(x)=0，则第m步的模型为［25］：

式(1)中：fm-1(x)—当前模型；T(x；Θm)—第m轮的回归树；Θm—第m步的决策树参数。

与二分类问题提升树和回归问题提升树不同，GBDT 算法中的损失函数（Loss Function）L(y，f(x)) 并无指定，可以自定义，这便使得GBDT 算法拥有更广泛的适用性。该算法的核心目标是所增加的每一个基学习器都应使得总体损失越来越小，即第m步应比第m-1 步的损失小：

将损失函数L(y，fm(x))进行一阶泰勒展开，代入上述不等式（推导过程略）［25］，得：

式（4）表明：回归树T(x；Θm)是通过拟合rm(x，y)来训练样本的。将(xi，yi) 代入rm(x，y)，即可得到rmi，进而得到第m步的训练数据集Tm：

式（5）中：n为样本数量，对rm1，rm2，…，rmn进行拟合，可得到第m棵回归树T(x；Θm)，其叶子节点的区域为Rmj，j= 1，2，…，J。

随后，更新基学习器［25］：

最终所得到的回归树为：

综上所述，GBDT 提升树的计算步骤为：计算当前损失函数L(y，fm( )x)的负梯度表达式rm(x，y)；通过rm(x，y)构造新的训练样本Tm并对其进行拟合；得到本步的回归树T(x；Θm)并更新本步的基学习器fm(x)；最后通过相加的方法将基学习器组合成一个强学习器，即最终的梯度提升（GBDT）决策树，进而得到预测结果。

2 GBDT 回归模型构建

2.1 数据集建立和预处理

本文的研究数据来源于国内、外64 篇文献中针对各类型膨润土进行的膨胀力实验研究结果。通过从文献中收集膨胀力实验的相关结果，对其中涉及的膨胀力影响因素进行归纳总结，初步建立了包含1 875条样本数据的数据集。

由于回归算法要求样本的每一特征均有具体值，而上述1 875 条样本中存在因文献说明不清而造成特征值缺失的部分样本，故对这些样本进行数据预处理，包括特征值补全和直接剔除。特征值补全方法为参考采用相似实验方法与材料的文献中的特征值来取值补全。对于难以补全的样本数据则直接剔除。完成数据预处理后，剩余1 063 条有效样本数据，以此作为建立机器学习模型的数据集。

通过结合对文献中实验现象的总结，参考各因素对膨润土膨胀力的影响机制以及对所制作的数据集进行分析，本文以目前世界上较为常见的15 种膨润土为研究对象，选取影响膨胀力的干密度、含水率、添加剂类型及掺入率、溶液成分及浓度因素为样本特征，以膨润土的膨胀力为样本标签，进行后续模型的构建。

数据集制作完毕后，对样本数量较多的8种膨润土（GMZ、Bamer1、Febex、Foca、Kunigel、Kyungju、MX80 和河南信阳膨润土）制作箱线图（图3）进行特征分析，能够较直观地得知各类膨润土的各个特征的取值分布。此外，数据集中各土类的样本数量也存在较大差异（图4），因产自我国内蒙古自治区兴和县的GMZ 膨润土目前产量较大、用途广泛且前人研究较为深入，故其样本数量最多，其次有Febex、MX80，以Avonsea 为最少。

图3 样本特征箱线图Fig.3 Box plots of the sample features

图4 不同类型膨润土的样本数量Fig.4 Number of samples for different types of bentonite

综上，数据集中样本特征分布的情况会对膨润土膨胀力预测模型造成一定的统计学影响，有与采用控制变量方法进行实验所得出的真实结果和规律存在出入的可能性，故用该数据集所搭建的模型并非意在解释膨润土的膨胀力机制，仅为复杂影响因素条件下的膨润土膨胀力提供预测参考。

2.2 模型构建

基于以上数据集的建立，本文以1063 条样本数据的土性、干密度、含水率、添加剂类型及掺入率、溶液成分及浓度这8 个膨胀力的影响因素为样本特征，以膨胀力为样本标签，并将数据集中的所有样本以3：1 的比例划分为训练集和测试集，利用Python 程序语言中sklearn.ensemble 库的GradientBoostingRegressor 类来构建梯度提升决策树回归模型（以下简称为GBDT 回归模型）。采用通过GridSearchCV 网格搜索结合手动参数调优，最终确定模型的最优参数如表1 所示。

表1 GBDT 回归模型最优参数Table 1 Optimum parameters of the GBDT regression model

其他未设置的参数如loss、splitter、subsample、criterion 、min_samples_leaf 、max_features 、alpha和 min_weight_fraction_leaf 即取默认值，见表2。

表2 GBDT 回归模型默认参数Table 2 Default parameters of the GBDT regression model

3 模型检验与分析

3.1 预测效果评估

GBDT 回归模型训练完成后对测试集样本的膨胀力值进行预测，输出训练集、测试集的膨胀力预测值，分别绘制真实值散点与预测值曲线（图5）并分别计算R2（模型评估指标）如下：

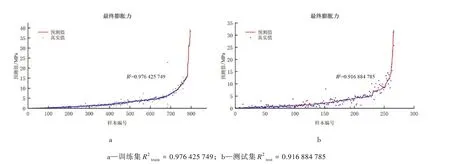
图5 真实值散点与GBDT 回归模型的预测值曲线Fig.5 Experiment data and the prediction curves of the GBDT regression model

模型的R2值能够反映回归模型的方程对样本标签（即膨胀力）的解释能力，即模型的预测准确率。R2越大，则表示模型越好。当模型为最理想效果，即预测值与真实值毫无偏差时，R2得到最大值1。

R2的计算公式如下［26］：

式（8）中：m—样本数量；yi—样本标签真实值；̂—样本标签预测值；—样本标签真实值的平均值。

GBDT 回归模型的R2train值和R2test表明模型对训练集、测试集的预测准确率分别为97.64%和91.69%。虽与训练集相比，测试集的预测准确率有所下降，但仍保持在90%以上的较理想状态，说明该模型并未存在较严重的过拟合情况，在兼顾预测准确率的同时具有良好的泛化能力。

3.2 模型成本分析

由于GBDT 回归模型的学习机制是前向分步算法，即模型每一步都仅学习一个弱学习器，在多轮迭代后逐步逼近优化目标，来实现梯度提升。并且，膨胀力预测问题属于回归问题，相比起分类问题具有较高的复杂度。因此，为了提高准确性而增加预测深度，GBDT 回归模型在训练过程中会产生成千上万颗决策树，对运行模型的机器硬件条件要求较高。

对此，本文将模型的预测效果与机器硬件条件共同纳入考虑，寻找能够兼顾上述两者的模型最优参数，称其为模型成本分析。

通过GradientBoostingRegressor 类的loss_函数输出模型的预测误差随所生成的弱学习器个数的变化（图6），得知拐点出现在第500 个弱学习器生成时，即模型于此时基本达到收敛。本文尝试利用n_estimators=500（即最多生成500 个弱学习器）这一参数重新进行模型训练，计算的模型R2如下：

图6 预测误差随弱学习器个数的变化Fig.6 Variation trend of the prediction error with the number of n_estimators

R2的计算结果显示，将模型生成的最大弱学习器个数由原来的1 500 个缩减为当前的500 个，相应的R2降低幅度非常小，仅从0.917降至0.901。虽然生成1 500 个弱学习器对机器来说并非难以企及，但在试图提高效率和不追求极致准确率的情况下，便可以采用缩减弱学习器个数的方法，找出图像的拐点，求得一个性价比最高的弱学习器个数值。

同理，除了n_estimators 外，其他参数也可通过绘制图像的方法寻找最优值（图7），缩减模型调参成本、减轻机器运行内存压力、提高模型训练性价比。

图7 预测误差随其他参数的变化趋势Fig.7 Variation trend of the prediction error with other parameters

3.3 模型预测效果评价

针对同样的数据集，本文运用Python 程序语言分别编写了多元线性回归模型、一般决策树回归模型、AdaBoost 决策树回归模型、随机森林回归模型的机器学习算法模型，对它们进行训练学习，得到各模所返回的膨胀力预测值、并与真实值进行比较，计算模型R2，绘制模型的膨胀力拟合曲线图（图8～11），从而评价与比较各模型的膨胀力预测效果。

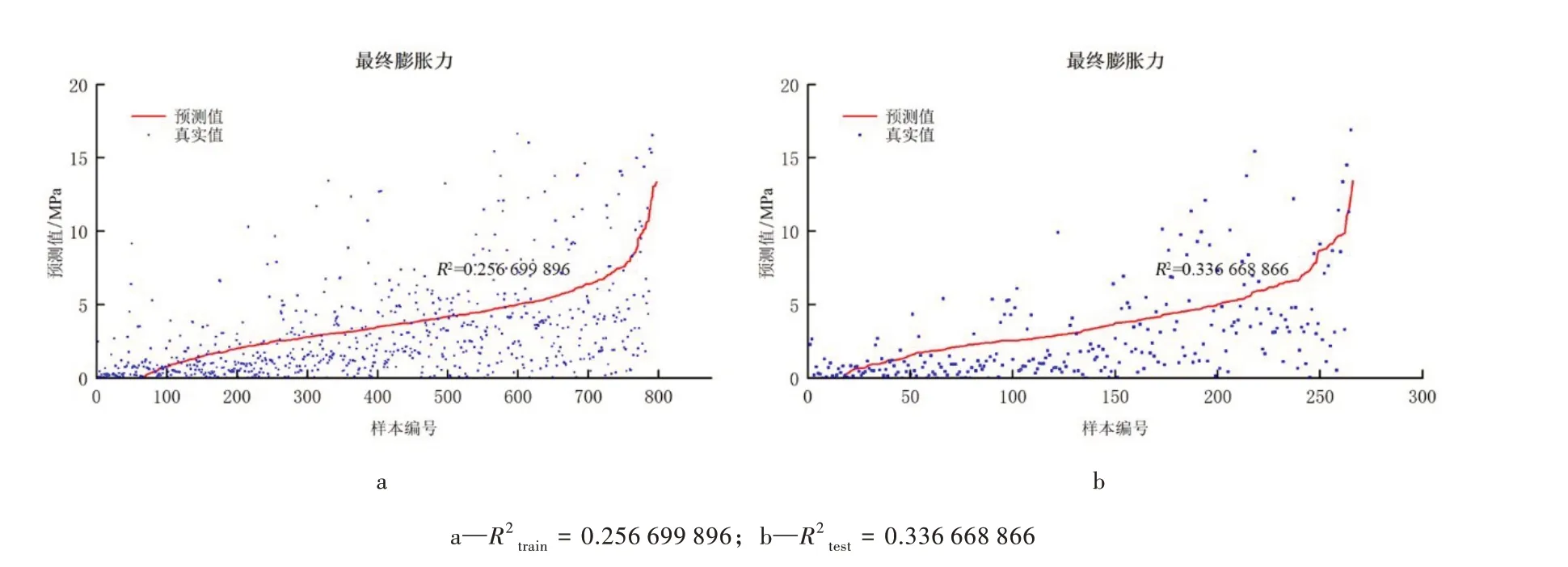
图8 多元回归线性模型预测效果Fig.8 The prediction results of Linear Regression with Multiple Variables

需要说明的是，本文在绘图前先将各模型的输出预测值分别进行升序排序，并以此来编号样本作为横轴，随后绘制预测值曲线和相应的样本编号下的真实值散点，以保证曲线单调和图像美观，因此相同的真实值数据集在不同模型的图像中呈现不同的分布情况。

多元线性回归模型由图8b 可见，该模型的预测准确率仅为33.7 %，说明线性回归并不适用于膨胀力预测。

一般决策树回归模型决策树是机器学习中常用于回归的监督学习算法，通过生成回归决策树来输出样本预测值。由图9b 可见，一般决策树回归模型的预测准确率为56.1 %，对测试集的预测准确率远低于训练集，存在过拟合现象，因此也不适用于膨胀力预测。

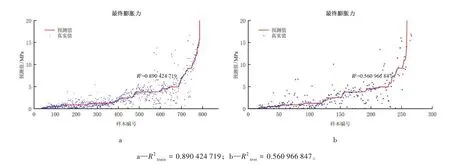
图9 一般决策树回归模型预测效果Fig.9 The prediction results of Decision Tree Regression

AdaBoost 决策树回归模型Boosting 是一种集成学习技术，在回归问题中表现突出。本文用其代表之一的AdaBoost 回归算法来优化一般决策树回归模型，形成AdaBoost 决策树回归模型。由图10a 和b 可见，该模型对训练集、测试集的预测准确率较一般决策树回归模型均有所提升，但78.8 %的准确率仍未达到本文预期。

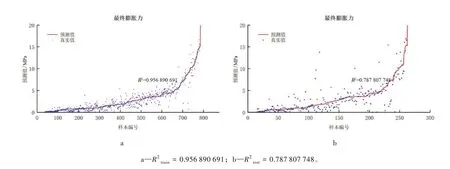
图10 AdaBoost 决策树回归模型预测效果Fig.10 The prediction results of Decision Tree Regression with AdaBoost

随机森林回归模型随机森林算法是一种基于Bagging 策略的集成学习算法，广泛运用于分类和回归任务中。由图11b 可见，随机森林回归模型较一般决策树回归模型预测更为准确，与AdaBoost 决策树回归模型预测水平相当，但仍未达到本文的预期效果。

图11 随机森林回归模型预测效果Fig.11 The prediction results of Random Forest Regression

为了便于比较，将以上四种机器学习算模型与GBDT 回归模型的R2值一同列于表3 中。通过对比R2值，容易看出GBDT 回归模型的预测准确性显著大于以上四种机器学习模型，证明了其在膨胀力预测方面具有良好的优越性与可行性，能够在实际工程中得到很好的应用。

表3 不同机器学习模型的R2 值比较Table 3 Comparison of R2 between different machine learning models

在地下实验室现场试验、高放废物深地质处置库的设计与处置库工程屏障投入实际运营中，对膨润土膨胀力产生影响的因素多而复杂，若采用传统的原位试验与室内试验，会存在工作量大、效率低下等问题，因此难以逐个、逐情况地快速取得这些因素的具体数值。经过本文的研究与分析，在评估了梯度提升决策树回归模型对膨润土膨胀力预测的准确率、模型成本的情况下，认为该模型能够兼顾预测的准确性和泛用性，并且能够快速地获取作为工程屏障的高压实膨润土砌块的膨胀力值，使高效评估工程屏障的工作性能及运营状态成为可能，值得在高放废物深地质处置的工程实践分析中推广和使用。