华家岭雾凇气候特征及预报方法研究

尚军林，雷 俊，姚玉璧，康 林，効碧鸿，李文举，郭俊彬

（1.中国气象局兰州干旱气象研究所/甘肃省干旱气候变化与减灾重点实验室/中国气象局干旱气候变化与减灾重点开放实验室，甘肃 兰州 730020；2.定西市气象局，甘肃 定西 743000；3.兰州资源环境职业技术大学，甘肃 兰州 730021）

雾凇是在湿冷环境里空气中过于饱和的水汽遇冷凝华，冻结在细长物体上的凝附物，多出现在我国北方高山、林区。学者对雾凇的形成条件、微物理过程等进行了广泛研究[1-2]，由于雾凇的分布具有明显的区域性特征，目前有关雾凇的研究多以区域为主，顾光芹等[3]对河北省雾凇时空分布特征及影响雾凇形成的关键气象因子进行了分析，吴素良等[4]对陕西省雾凇分布特征及其物理特征进行了研究，周宏飞等[5]对新疆北部影响雾凇形成的气象因子进行了分析，结果表明，低温、充足的水汽条件、较小的风速或者静风是雾凇形成的重要条件，主要环境成因包括准静止锋、大气垂直结构和逆温层，同时还受到地形、高度等的影响，雾凇通常发生在冻雨、过冷雾、湿雪三种天气条件下[6]，在高山的山顶和冬季迎风坡面地带更易形成雾凇[7]。

雾凇作为一种旅游资源或冰冻灾害，受到国内外学者的关注[8-13]，赵珊珊等[14]、王遵娅等[15]研究表明，受气候变暖影响，中国雾凇日数呈减少趋势，雾凇天气的发生频次与平均气温呈显著负相关。李文静等[16]研究表明，我国雾凇主要出现在江南中北部、贵州中西部及其以北地区，其中北方雾凇分布最广。国内学者也对黄山[8，17]、大兴安岭[18]、衡山[19-20]、长白山[21]等著名旅游景点雾凇形成的气候条件和时空分异规律进行深入研究。

雾凇的预报也是雾凇研究的热点问题之一，国外学者建立了Lenhard、Jones、Imai、Makkonen 等雾凇预报模型[9-10]，Lenhard 模型基于经验，模型过于简单，相关性低，预测效果较差；Jones 和Imai 模型利用逐时资料模拟雾凇的形成过程，参数易于获取，在描述物理过程的同时考虑雾凇随时间的变化以及输入参数的变化；Makkonen 模型是一个与时间相关的数值模型，给出了雾凇增长量与碰撞率、收集率、冻结率以及液态含水量的关系，模拟效果较好。许剑勇等[22]利用影响雾凇景观形成的关键气象因子建立了黄山雾凇旅游气象指数，经实践检验准确率较高，可为气象业务应用提供参考。各地气候特点不同，气象指数的适用性不同，对于山区气候特征明显的华家岭雾凇预报方面研究较少。

华家岭位于甘肃省中部，属典型黄土高原半干旱气候区，海拔2 450.6 m，雾凇的变化特征及其与气象要素的关系具有代表性，尹宪志等[23]对华家岭电线积冰在不同高度、不同方向、不同导线的变化特征及与气温、水汽压、风速等气象要素的关系进行了研究，有关气候变暖背景下华家岭雾凇时空变化特征、影响雾凇形成的气象因子和预报方法的研究较少，本文基于华家岭气象站1951—2020 年气象资料，分析华家岭山区雾凇气候特征和形成条件，并利用判别分析法建立基于常规预报要素的雾凇预报模型，以期为区域防灾减灾及旅游业发展提供参考。

1 资料和方法

1.1 资料来源

利用华家岭气象站1951—2020 年地面气象观测资料及2021 年9 月—2022 年4 月雾凇逐时资料，当日有雾凇发生定义为一个雾凇日。采用气象统计常用的四季划分：冬季（12 月—次年2 月）、春季（3—5 月）、夏季（6—8 月）、秋季（9—11 月）。

2020 年4 月1 日后因观测业务调整，华家岭气象站雾凇人工观测被取消，故本文21 世纪10 年代资料使用2011—2019 年平均资料代替，年际变化不分析2020 年，月际变化4—12 月均值采用1951—2019 年69 a 均值，春、夏、秋季变化特征分析采用1951—2019 年资料，冬季变化特征分析采用1951—2020 年资料，雾凇预报实际效果检验中应用2021年9 月—2022 年4 月智能天气现象仪逐时观测资料。

1.2 分析方法

1.2.1 气候倾向率

气象要素变量Yi公式如下：

式中：ti表示Yi对应的时间，a 为回归常数，b 为回归系数，n 为样本量。

式中：b 为气候变化倾向率，一般以10b 表示某要素的气候变化倾向率。

1.2.2 Mann-Kendall 突变检验

Mann-Kendall 检验法是气象、气候学中常用来进行突变检验的一种方法[24]。设原始时间序列为d1、d2、…、dn，ri表示第i 个样本di＞dj（1≤j≤i）的累积数，

在原序列随机独立等假设下，Sk的均值和方差分别为。将Sk标准化得：

再按逆序列重复上述过程计算UB（k）。给定显著性水平α=0.05，统计量UF 和UB 的临界值为±1.96。UF（k）＞0，表示序列呈上升趋势；反之，呈下降趋势。＞1.96 或＜1.96，表示上升或下降趋势明显。如果UF 和UB 两条曲线出现交点，且交点在临界直线之间，交点对应时刻就是突变开始时间。

1.2.3 Bayes 逐步判别分析

判别分析用于判断一个样品的所属类型，被广泛运用于天气现象的预报。逐步判别是针对多组判别因子，每一步对某一判别因子进行检验，确定该因子是否该剔除，最后逐步得到只含通过检验的因子从而建立判别方程的方法。Bayes 判别分析是结果较为可靠的一种判别分析方法，其主要思想是充分利用各类别的先验信息，根据已有样本的数据信息，总结客观事物的规律并建立判别函数并对其进行分类[25]。采用Bayes 建模方法需要满足2 个条件才能进行业务应用：（1）建模样本的数量不能少于变量数量的8 倍；（2）模型回判验证的准确率＞80%。

对于分为m 个组的研究对象，判别函数一般为：

式中：Yk是判别指标，由研究的对象决定；xk1、xk2、…、xkn是研究变量，ak1、ak2、…、akn是判别系数，Ck为常量。

Bayes 原理可用下式表示：

式中：Ck（k=1，2，…，m）为n 个指标的总体，fk（x）为各类别样本集的概率密度函数；pk为概率密度函数的先验概率。当P（Ck|X）（k = 1，2，…，m）为组内最大值时，确定X∈Ck。

选用1951—2020 年逐日气象资料，因5—9 月雾凇日仅占全年的1.7%，本文仅对10 月—次年4月做预报，连续雾凇日往往首日为雾凇生成日，之后数日处于保持或者消融阶段，故预报时出现连续雾凇时只取首日，排除资料有空值的日期。选取与雾凇相关度较高的日平均气温、日最高气温、日最低气温、日平均水汽压、日平均相对湿度、日最小相对湿度、平均风速等7 个基础气象要素和当日有无降水、前一日有无降水、平均气温日较差、平均水汽压日增量、平均相对湿度日增量、最小相对湿度日增量等6个计算量共13 个变量作为预报因子，为了使各变量具有统一的特征值，首先对各变量进行标准化处理，利用Bayes 判别分析法及SPSS 19.0 统计分析软件对10 月—次年4 月资料分月进行逐步判别分析，建立华家岭雾凇逐月预报模型，并用建模资料进行回判验证。模型通用方程为：

式中：Y0为无雾凇判别方程，Y1为有雾凇判别方程，x0i、x1i（i=1，2，3，…，13）为判别因子，分别对应平均气温、最高温度、最低气温、平均相对湿度、平均风速、平均比湿、最小相对湿度、日较差、相对湿度较前一日增量、最小相对湿度较前一日增量、比湿较前一日增量、当日有无降水、前一日有无降水，C0、C1为常量，a1i、a0i（i=1，2，3，…，13）为对应的判别系数。若判别结果Y1＞Y0则预报有雾凇，否则预报无雾凇。引入建模资料回代至判别方程，检验判别方程的预报准确率PC、TS评分、空报率FAR、漏报率NAR，设预报没有雾凇准确次数为NA、空报次数为NB、漏报次数为NC、准确预报次数为ND，则：

2 结果与分析

2.1 华家岭雾凇气候特征

2.1.1 华家岭雾凇起止时间、持续时间变化特征

1951—2020 年华家岭年平均雾凇日数为69.1 d，雾凇日数1959 年最多，为110 d，2016 年最少，为28 d；雾凇平均初日在10 月15 日，最早出现在9 月6 日（1993 年），平均终日在4 月25 日，最晚出现在6 月8 日（1970 年）；雾凇最长持续时间为27 d，出现在1964 年1 月3 日—1 月29 日和1988 年12 月21 日—1989 年1 月16 日。

2.1.2 华家岭雾凇的季节分布特征

对1951—2020 年华家岭雾凇日数季节变化特征分析表明，冬季雾凇日数最多，为37.3 d，占全年的53.4%，1964 年最多，为62 d，1953 年最少，为10 d；春季次之，平均雾凇日数为18.1 d，占全年的25.9%，1991 年最多（37 d），2014 年无雾凇，为最少年；秋季平均雾凇日数为14.3 d，占全年的20.5%，1967 年最多（34 d），1955 年最少（3 d）；夏季共出现4 次雾凇，平均占全年的0.014%。

2.1.3 华家岭雾凇的月分布特征

对华家岭月平均雾凇日数（图1）进行分析，11月—次年3 月雾凇出现频率最高，为59.9 d，占全年雾凇日数的86.9%，2 月最多，平均雾凇日数为13.1 d，占全年的19% 。华家岭1 a 内除7、8 月其余月份均有雾凇出现。

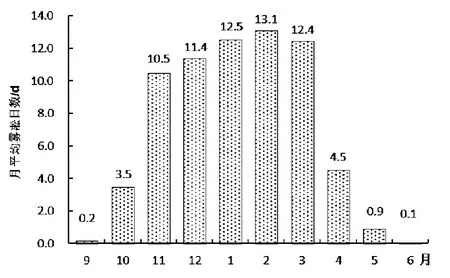
图1 华家岭雾凇月平均日数

2.2 华家岭雾凇日的气象条件分析

影响雾凇形成的因素主要有地形、海拔和气象因素等，其中最主要因素为温度、湿度、风等气象条件。利用箱线图法对华家岭雾凇出现时的日平均风速、日平均气温、日平均比湿、日平均相对湿度等气象条件（图2）分析，结果显示，雾凇日日平均气温最高为5.6 ℃，最低值为-23.1 ℃，均值为-6.0 ℃，中位数为-5.8 ℃，下四分位数为-8.9 ℃，上四分位数为-2.6 ℃，表明雾凇出现时温度集中在-8.9～-2.6 ℃。雾凇的本质是水汽的凝结，最低气温是影响雾凇形成的关键因素，其形成条件要求环境温度必须低于0 ℃，华家岭雾凇日最低气温最大值为0.9 ℃，最小值为-25.5 ℃，均值为-8.6 ℃，中位数为-8.2 ℃，下四分位数为-11.6 ℃，上四分位数为-5.0 ℃。雾凇出现时水汽充足，日平均相对湿度均值为83.7%，下四分位数为76%，上四分位数为94%，相对湿度＜65% 时，出现雾凇的概率＜10%；日平均比湿均值为3.5 g/kg，下四分位数为2.4 g/kg，上四分位数为4.4 g/kg，对于雾凇出现频次最高的冬春季，日平均比湿为3.5 g/kg，为研究区较大值。合适的风速范围对雾凇的形成很重要，风速过小时，目标物水滴捕获不足；风速过大时，水滴在目标物上冻结时间不足，华家岭雾凇出现时，日平均风速下四分位数为2.6 m/s，中位数为3.8 m/s，上四分位数为5.3 m/s，均值为4.0 m/s，最有利于雾凇形成的风速条件为2.6～5.3 m/s。当日平均气温为-8.9～-2.6 ℃、最低气温为-11.6～-5.0 ℃、日平均风速为2.6～5.3 m/s、日平均相对湿度≥65%时，出现雾凇的概率较大。

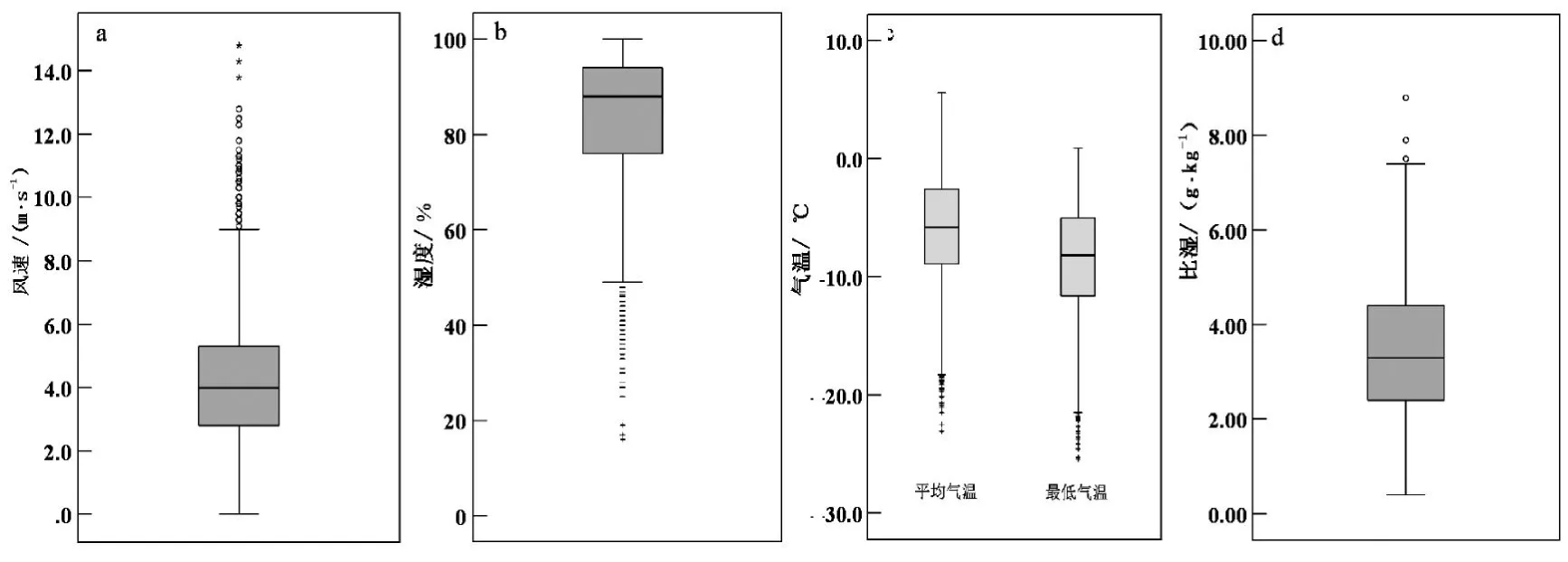
图2 1951—2020 年华家岭雾凇相关气象条件统计箱线图

对华家岭夏季雾凇日及其气象条件进行分析（表1），结果表明，低气温是夏季雾凇形成条件之一，夏季雾凇最低气温均＜0 ℃，这是雾凇形成的必备条件；其次有冷空气侵入，24 h 变压均＞4.0 hPa，日降温幅度＞3 ℃，说明有明显冷空气入侵；三是湿度高，雾凇日平均相对湿度均＞63%并伴有降水；四是较大的风速，夏季雾凇日平均风速为5.3～8.8 m/s，位于秋、冬、春三季有利于形成雾凇的风速条件上四分位数之上（2.6～5.3 m/s），说明夏季需要更强的冷空气及其所引发冷平流才有利于雾凇形成。华家岭夏季雾凇形成的另一个重要因素是地形条件，华家岭位于黄土高原西边界，属温带高寒山区，山体呈东北—西南走势，与冷空气路径基本垂直，干冷空气南下时在华家岭北坡迎风受迫抬升，强度增强，加之该区域夏半年受夏季风影响水汽充足，易形成夏季雾凇。

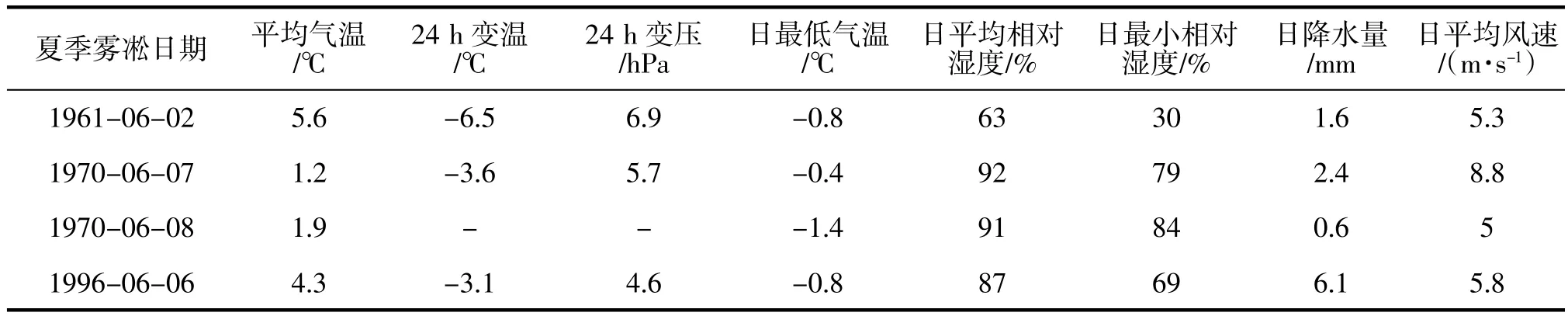
表1 华家岭夏季雾凇及气象条件分析

2.3 华家岭雾凇的气候变化特征

2.3.1 华家岭雾凇年代际变化特征

由1951—2020 年华家岭雾凇日数年代际变化（图3）可知，华家岭年代际平均雾凇日数为47.0～80.2 d，20 世纪90 年代最多（80.2 d），80 年代次之（78.6 d），21 世纪10 年代雾凇日数最少，为47 d。20世纪年平均雾凇日数变化较小，总体呈波动上升趋势，进入21 世纪后明显下降，21 世纪00 年代和10年代分别较20 世纪90 年代减少19.6%和27.1%。21 世纪10 年代与其他各年代平均雾凇日数差异显著，通过0.01 的显著性检验。

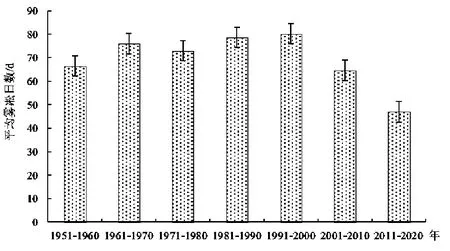
图3 1951—2020 年华家岭雾凇日数年代际变化

2.3.2 华家岭雾凇年际变化特征

根据华家岭气象站1951—2020 年气候资料，利用气候倾向率分析雾凇年际变化趋势、利用Mann-Kendall 法进行突变分析和趋势分析。结果表明，70 年来雾凇日数呈下降趋势，气候倾向率为-2.5 d/10 a（图4a）。对年雾凇日数进行突变检验（图4b），结果显示1950—1952 年、2009—2019 年UF（k）＜0，表明该时期雾凇日数呈减少趋势，2018 年显著减少；1953—2008 年，UF（k）＞0，表明雾凇日数呈增加趋势，其中，1957—1962 年增加趋势显著（P＜0.05），UF（k）和UB（k）曲线在2015 年相交，且交点位于临界线之间，判定2015 年为突变年。综上，70年来华家岭雾凇日数呈波动下降趋势，1957—1962年显著增加，2018 年后减少显著，2015 年为突变年。

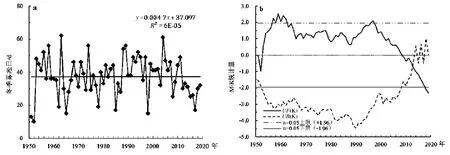
图4 1951—2019 年华家岭雾凇日数年际变化（a）及突变检验（b）

2.3.3 雾凇日数的季节变化特征分析

2.3.3.1 春季雾凇

由春季雾凇日数的年际变化（图5）可知，近70年华家岭春季雾凇日数整体呈减少趋势，气候倾向率为-1.2 d/10 a。1998 年前呈波动上升趋势，气候倾向率为2.5 d/10 a，1998 年后以4.3 d/10 a 的速率下降。Mann-Kendall 突变检验表明，1953—1998 年UF（k）在临界线上下徘徊，春季雾凇日数总体呈较为明显增加趋势，2015 年后显著下降（P＜0.05），UF（k）和UB（k）曲线在2012 年相交，通过对比雾凇日数序列，2012 年为有效突变年。

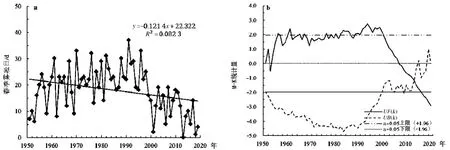
图5 1951—2019 年华家岭春季雾凇日数年际变化（a）及突变检验（b）

2.3.3.2 夏季雾凇

李文静等[16]对中国雾凇分布情况进行分析发现，夏季雾凇分布极少，主要分布在西藏、青海等个别地方，黄土高原夏季雾凇极为罕见。华家岭由于其特殊的地理环境，有气象观测记录以来，1961、1970、1996年夏季6 月出现雾凇4 次，尤其是1970 年6 月7—8 日连续2 d 出现雾凇。

2.3.3.3 秋季雾凇

华家岭1951—2019 年秋季雾凇日数变化如图6 所示。秋季雾凇日数总体呈波动减少趋势，气候倾向率为-1.5 d/10 a（图6a）；1951—1998 年雾凇日数呈波动增加趋势，1958—1965、1967—1969 年增加显著（P＜0.05）；1998 年后呈现减少趋势，2010 年后减少趋势更加明显，秋季UF（k）和UB（k）曲线有3个交点，分别是1998、2000 和2004 年，对比雾凇日数序列确定2004 年为有效突变年。

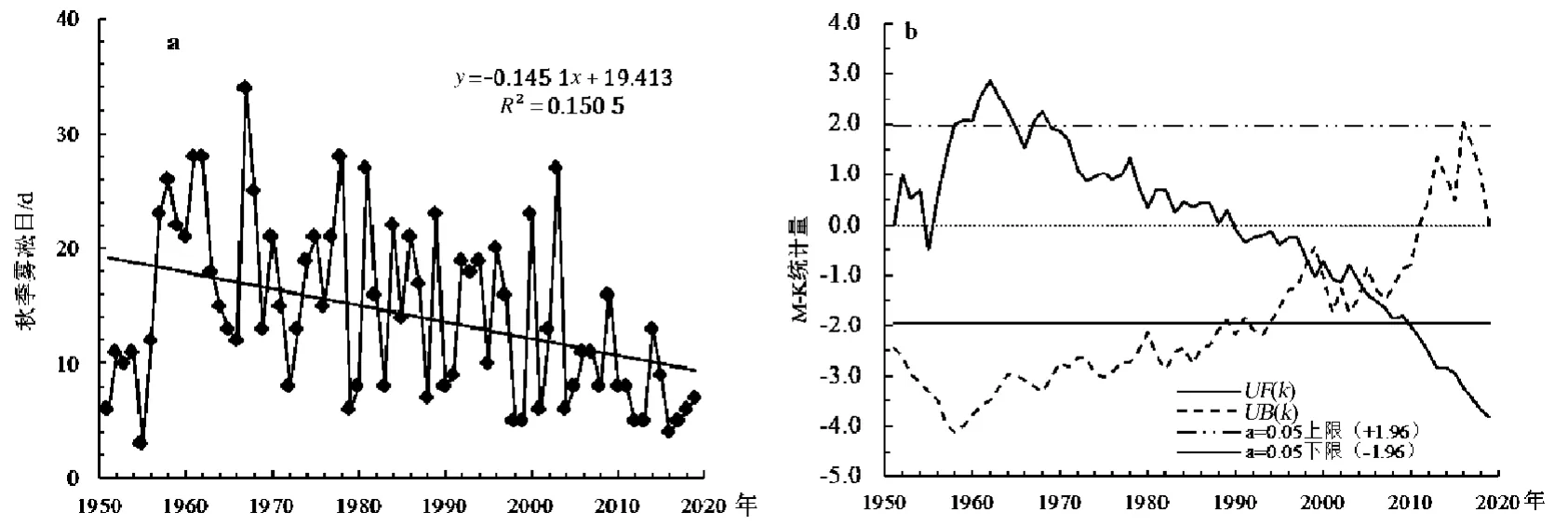
图6 1951—2019 年华家岭秋季雾凇日数年际变化（a）及突变检验（b）

2.3.3.4 冬季雾凇

因无1950 年12 月雾凇资料，本文冬季雾凇日数分析时段为1952—2020 年。对冬季年雾凇变化特征分析（图7）表明，冬季雾凇日数整体气候倾向率为0.05 d /10 a，无显著线性趋势，年际变幅较大。Mann-Kendall 突变检验结果表明，UF（k）与UB（k）曲线交点在1953、1959、1972、1979、2015 年，但根据雾凇日数序列判断，70 年来华家岭冬季雾凇日数并无显著增加或减少时段，故冬季雾凇无有效突变年。

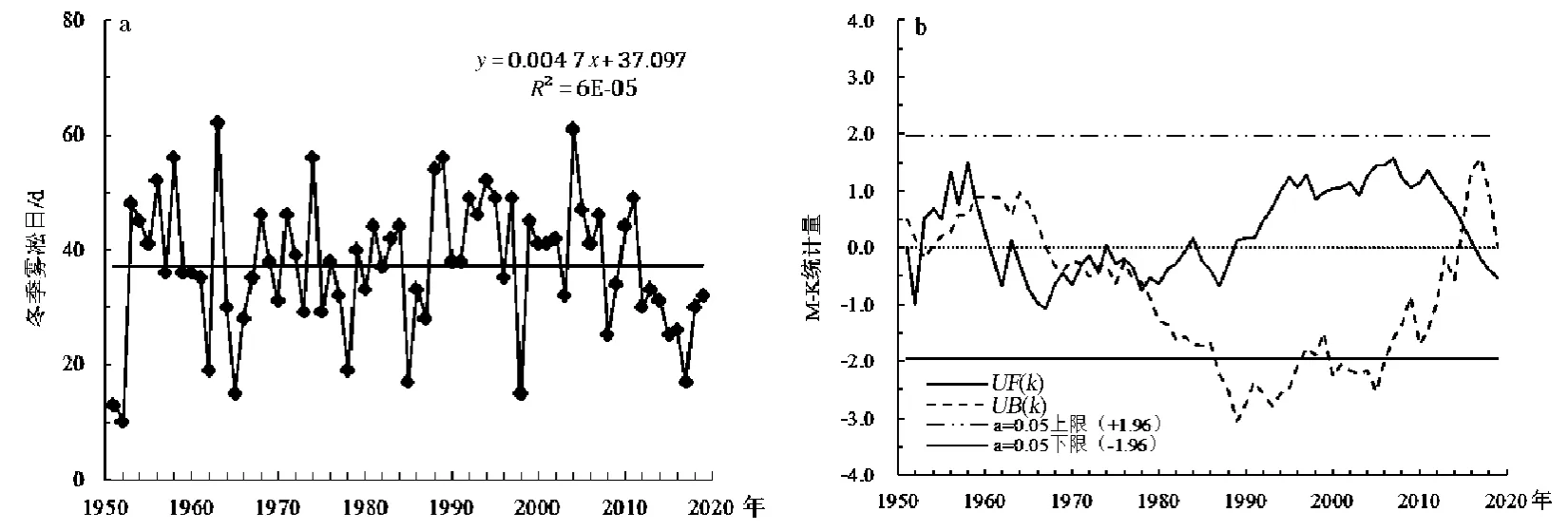
图7 1952—2020 年华家岭冬季雾凇日数年际变化（a）及突变检验（b）

综合分析华家岭雾凇日数分布及其的季节变化（图5～7）可知，近70 年来，各季节变化趋势存在差异，春季（-1.2 d/10 a）、秋季（-1.5 d/10 a）呈减少趋势，其中秋季减少趋势更明显，冬季（0.05 d/10 a）呈微弱增加趋势。

2.3.4 华家岭雾凇月变化特征

对华家岭雾凇月变化（表2）进行分析发现，华家岭雾凇日数月变化趋势不一致，其中1 月呈增加趋势，线性倾向率为1.0 d/10 a，未通过0.05 的显著性检验；其余月份均呈现减少趋势，4、10 月减幅＞3.7 d/10 a，通过0.01 的显著性检验；2 月变化最小，为-0.3 d/10 a。

表2 华家岭1951—2020 年各月雾凇日数变化

2.4 华家岭雾凇预报模型及检验

2.4.1 华家岭雾凇预报模型建立

利用Bayes 逐步判别法对10 月—次年4 月资料进行逐步判别，建立华家岭雾凇逐月判识模型，应用本文建立的判识模型和常规预报因子，建立华家岭雾凇预报模型。表3 为各月判别方程对应系数、常量及回判验证结果，表中系数为0.0 表明该因子未通过检验或因子作用不明显，系数绝对值越大，则该因子对预报雾凇越敏感。由表3 可知，各月敏感的判别因子不尽相同，但多与日平均气温、日平均相对湿度和日平均相对湿度较前一日增量有关。

表3 华家岭雾凇分月判别系数及回判验证结果

由回判验证结果可知，逐月判别方程回判准确率为84.0%～90.8%，均＞80%，且样本数量远远大于因子量的8 倍，满足Bayes 建模方法业务应用的2个条件。但从TS检验来看，各月TS评分均较低，在36.4%～52.0%，TS评分低的主要原因是空报率偏高，4、10、11 月空报率＞50%，10 月达到60.8%，对比月雾凇空报率（表3）和月雾凇日数（图1）可知，4 月（4.5 d）、10 月（3.5 d）平均雾凇日＜10 d，雾凇日数越少，空报率越高，空报率与月雾凇日数呈反比，可见在本文研究的气象条件下华家岭易于形成雾凇的日数要多于实际雾凇日。

2.4.2 华家岭雾凇预报模型应用检验

利用华家岭气象站2021 年9 月—2022 年4 月智能天气现象仪雾凇逐时观测资料和气温、湿度、风速等因子进行预报应用检验（表4）。各月预报准确率为71.4%～96.8%，TS评分为0.0%～75.0%，空报率为25%～100.0%，漏报率为0.0%～25.0%，空报率较高的10 月和3 月都未出现雾凇，且空报次数仅为1次，预报效果较好。

表4 2021 年9 月—2022 年4 月华家岭雾凇预报检验

3 讨论

雾凇作为旅游资源或气象灾害对我国社会和经济的影响较大，研究表明，我国雾凇主要出现在中国北方地区，尤其是新疆北部、东北中部和南部、黄河中下游等地[15]，且存在明显的时空分布特征。对华家岭雾凇气候特征分析发现，研究区雾凇主要集中在冬季，夏季发生的频率最小，与赵珊珊等[14]对中国雾凇研究的结论一致。对研究区雾凇月分布特征分析发现，华家岭雾凇主要出现时段为11 月—次年3月，与已有研究结论一致，2 月雾凇出现频次最多，1月次之，赵珊珊等[14]基于全国603 个站的雾凇观测资料研究表明，中国雾凇出现频率1 月最大，12 月次之，与本研究区研究结论存在差异。本研究中，华家岭雾凇天气过程主要出现在20 世纪90 年代以前，较全国大范围持续性雾凇天气过主要出现在20世纪80 年代的研究结论明显滞后[15]。

气温、相对湿度和风速等气象因子对雾凇的形成有重要影响[26-27]，研究区秋、冬和春季雾凇形成的重要因素均为日平均气温、最低气温、风速和相对湿度，强冷空气入侵及其所引发的冷平流是研究区夏季雾凇形成的重要原因，此外，地形因素也是华家岭夏季雾凇形成的主要因子之一。

受气候变暖影响，我国冷事件出现频次呈现显著下降趋势[28]，我国大部分地区雾凇发生频次同样减少，发生频次与气温呈现显著负相关[14-15]，张志富等[29]对1961—2012 年中国雾凇时空变化特征的研究表明，中国年雾凇日数总体呈减少趋势（-0.6 d/10 a），北方地区减少最明显，长江中下游部分站点有增加趋势，呈现较明显的区域差异特征，孔锋等[30]研究表明，中国雾凇日数减少具有明显的纬向差异，高纬地区减少趋势大于低纬地区，且沿江沿河减少趋势大。本研究中，华家岭雾凇日数总体呈下降趋势，气候倾向率为-2.5 d/10 a，与已有研究结论基本一致[14，29]。突变检验研究表明，20 世纪80 年代末，中国雾凇天气过程出现了突变减少，华家岭雾凇在21 世纪10年代出现了突变减少，较全国明显推迟，减小趋势则更明显，主要原因为区域对气候变暖的响应差异及研究期不同等造成。

廖玉芳等[31]、梁岱云等[32]等对雾凇预报方法进行研究，建立了基于逐时资料的雾凇增长经验模型及雾凇观光指数等。本研究基于Bayes 判别分析法建立了华家岭雾凇预报模型，经试报检验，预报准确率在74%以上，模型简单，基础资料易于获取，便于实现雾凇预报自动化、智能化，具有较好的业务应用效果，该模型使用实况气象要素建立，在业务中则要嵌套常规预报场资料作为预报因子，模型预报准确率还将依赖于常规预报结论准确性，结合高空形势场和大气环流因子等因素或能进一步提高雾凇预报准确率。

4 结论

基于华家岭国家基本气象站1951—2020 年气候资料，应用Mann-Kendall 突变检验、气候倾向率、箱线图法等方法对华家岭雾凇气候变化特征和影响雾凇形成的气象因子进行分析，基于Bayes 逐步判别法建立华家岭雾凇预报模型，得出以下结论：

（1）华家岭年平均雾凇日数为69.1 d，最多110 d，最少28 d，平均初日为10 月15 日、终日为4 月25日，最长持续时间为27 d，主要出现在冬季，其次是春季和秋季，夏季共出现4 次雾凇。1 a 内除7、8 月其余时间均有雾凇出现，2 月雾凇日数最多。

（2）影响华家岭雾凇形成的主要气象因子是温度、湿度和风，华家岭雾凇日气温集中在-8.9～-2.6 ℃、最低气温集中在-11.6～-5.0 ℃、风速维持在2.6～5.3 m/s、相对湿度＞65%。

（3）华家岭年雾凇日数呈减少趋势，气候倾向率为-2.5 d/10 a，2018 年后减少显著，2015 年为突变年。雾凇的变化呈明显的季节差异，秋季减少趋势最明显（-1.5 d/10 a），其次为春季（-1.2 d/10 a），冬季（0.05 d/10a）呈微增加趋势。4、10 月雾凇日数减少趋势最明显（P＜0.01），气候倾向率均为-3.7 d/10 a，1、2 月年际变化最小。

（4）利用Bayes 逐步判别法建立雾凇预报模型，经回判检验，模型分月预报准确率为84.0%～90.0%，漏报率为8.7%～16.2%，试报准确率为71.4%～96.8%，预报性能好，且模型中应用变量为常规预报参量，易于获取，可应用于业务实践。