算法视角下的微积分

焦华

（贵州商学院，贵州贵阳 550014)

微积分的英文名称——calculus，来源于拉丁文中的“石子”“演算”词语，换句话说,微积分的本质就是一种演算法则或计算方法。因此不要觉得微积分有多神秘，它就像大家熟知的加减乘除四则运算一样，只是众多计算方法中的一类算法而已。

从微积分字面释义来看:微分——顾名思义就是事物微小的部分——事物似零非零的部分，这个似零非零的部分从哪里而来？它是从某个事物整体无限细分得来，这是化整为零的过程；而积分——它是积累、累积的部分，是无限求和的过程。和之前正好相反，它是求微小部分的和，也就是求似零非零部分的和，这是积零为整的过程。微元法是用定积分解决实际问题的基本思想、基本方法，其本质就是先化整为零，再微元替代，最后积零为整。

1 高级语言中的函数概念

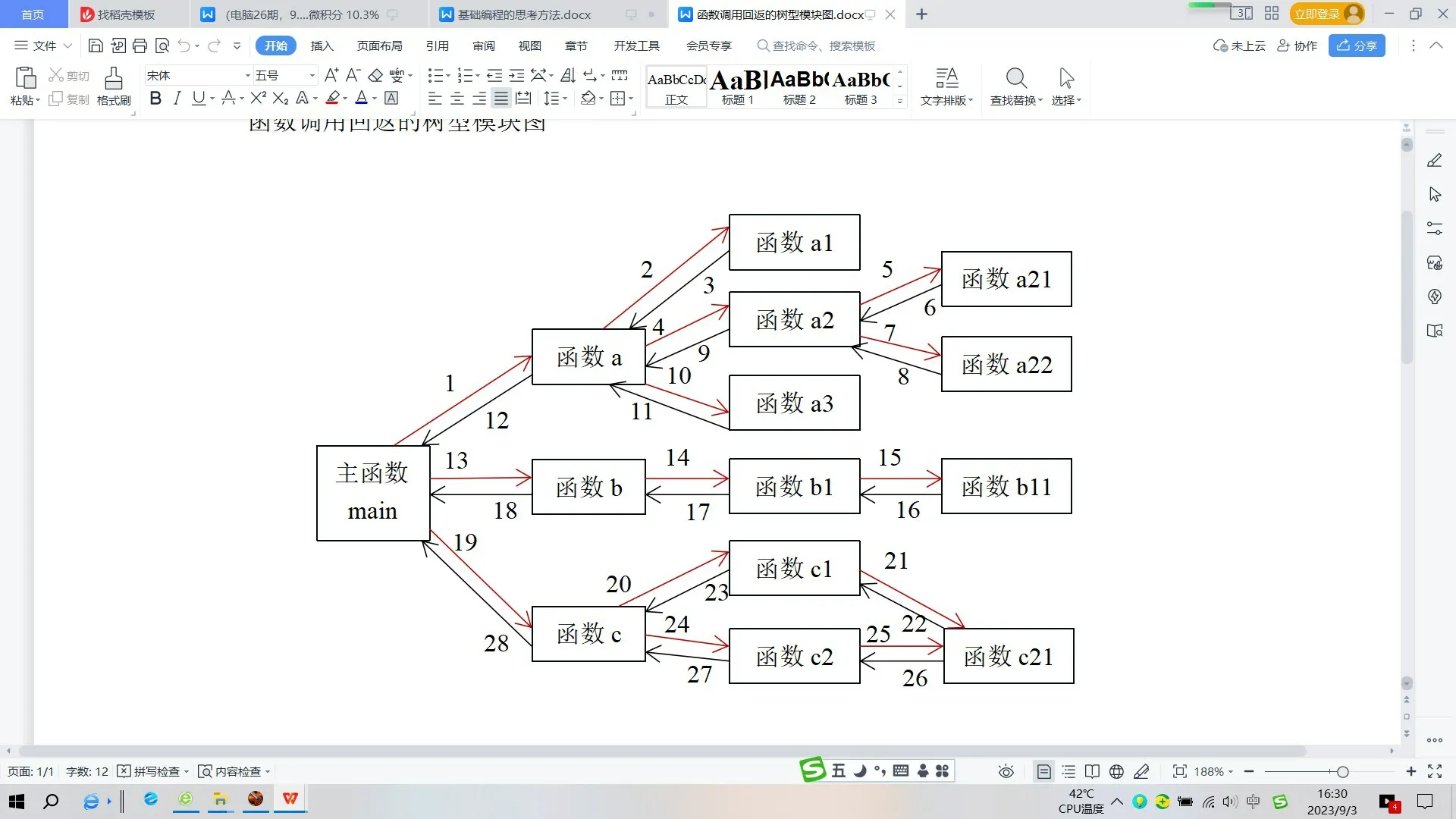
图1 函数调用返回的树型模块图

函数是微积分的主要研究对象，函数的极限、函数的连续、函数的导数与微分、函数的积分是贯穿微积分始终的内容。函数是科学史上流行了200多年的一个基本概念，因此深刻地影响了其他学科……计算机过程化高级语言中的函数其实就是程序代码中的子程序，更有甚者C 语言里的主程序也是函数(main()主函数），强大的高级语言的一个重要指标就是它拥有丰富的内部函数。图1是C语言中的一个函数调用返回的树型模块图[1]。

函数调用返回、参数传递、局部量与全程量、嵌套调用与递归调用等是很多高级语言的重点和难点[2]，教学过程中学生往往感到困惑和无所适从，但从微积分的角度看，也就是一个有限次的多重复合函数而已。

2 函数的改变量（增量）是贯穿微积分始终的线索

函数的改变量（增量）是贯穿微积分始终的线索，而编程计算函数增量很简单。函数改变量（增量）的定义如下：设x0为函数y=f(x)定义域内一点，自变量x在x0处取得增量Δx，Δx=x-x0，x=x0+Δx 在定义域内，则f(x0+Δx)-f(x0)称为在x0点的函数增量（或改变量），记为Δy。用示意图表达如下[3]：

函数y=f(x),由自变量增量Δx产生函数增量Δy,

用函数图形表示如下（含Δx > 0 和Δx < 0 两种情形）：

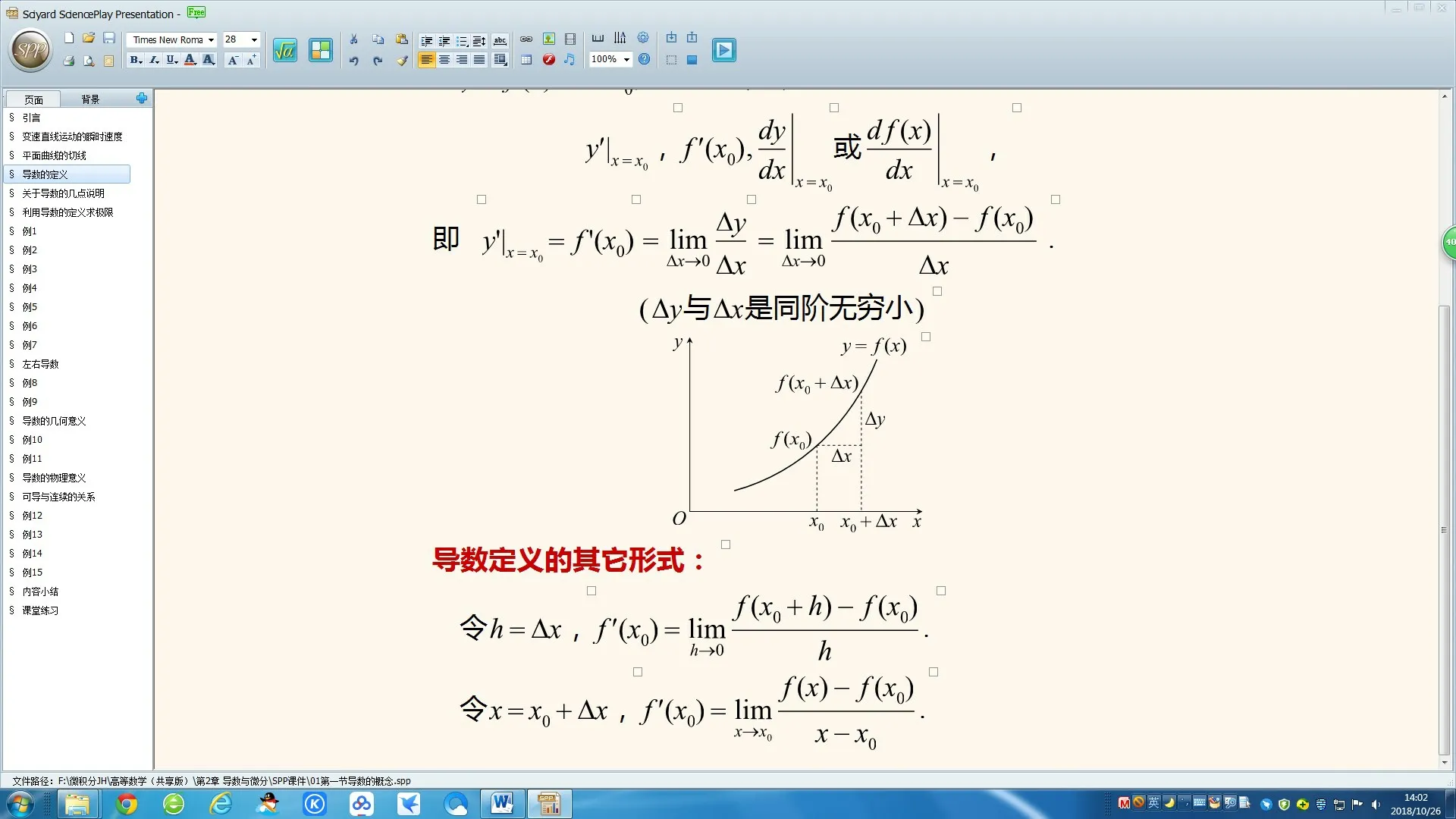
图2 函数（正）增量图

图3 函数（负）增量图

下面将会看到微积分中的重要概念和内容和函数增量有关：

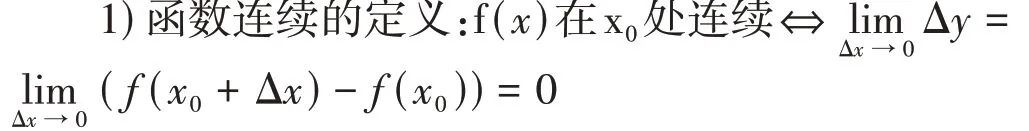
定义说明函数连续表达的是自变量的微小变化只会引起对应函数的微小变化。

2)函数导数的定义：

根据导数的定义，函数求导的算法步骤如下：

①计算函数的增量：Δy=f(x+ Δx) -f(x);

3)函数微分的定义：设函数y=f(x)在某个区间上有定义，x0和x0+ Δx在此区间内，若函数增量Δy=f(x0+ Δx) -f(x0)可表示为Δy=A· Δx+o(Δx)，这里A是和Δx无关的常数，则称函数y=f(x)在x0点处可微，并称A· Δx为函数y=f(x)在x0点相应于自变量增量Δx的微分，记作dy，即：dy=A· Δx。

将以上定义通俗化，如果在某点的函数增量Δy用自变量增量Δx 线性表示，误差仅是Δx 一个高阶无穷小，则称函数f(x)在此点可微,微分dy即是函数增量Δy的线性主部。

重要定理：函数y=f(x)在x0点处可微的充要条件是它在x0点处可导，而且微分和导数关系是：dy=f′(x0)· Δx[3]。

4)导数在经济学中的应用——边际与弹性

边际与弹性从语义上理解，只能是指定状态下的微小改变。这里反映的是函数的绝对变化率和相对变化率（绝对导数与相对导数）。具体概念对比表述如下：

取Δx= 1，即自变量在x处改变一个单位时，若这个“单位”很小或相比x值很小时，则：

即Δf≈f’(x)，此式的意义是：当自变量在x 处改变一个单位时，函数f(x)的改变量可近似用f’(x)来表示，即改变了f’(x)个单位，此为边际的经济意义。

取Δx/x= 1%，即自变量在x处相对改变1%时，

上式的意义是：当自变量在x处相对改变1%时，函数f(x)的相对改变量大致为Ey/Ex%，此为弹性的经济意义。

5)不仅微积分上述的基本概念和函数改变量有关，微积分中重要的定理、公式也和函数改变量有关。比如：拉格朗日中值定理：f(b) -f(a) =f′(ξ)(b-a)。

结论：函数的改变量（增量）是贯穿微积分始终的线索。这部分涉及的极限运算可用高级语言中的循环结构实现，由循环语句中的条件表达式控制精度。

3 定积分的近似计算

定积分是积分学中重要的内容，起源于生产实践中面积和体积等的计算问题。回顾初等数学中面积计算的相关内容：（由）长方形面积的定义→（推出）平行四边形面积公式（拼接法）→（推出）三角形面积公式（拼接法）→（推出）梯形面积公式（拼接法）→“穷竭法”“割圆术”得到圆面积公式。数学中的重要概念并非无中生有，而是从客观世界的现实原型中抽象出来的，比如“曲边梯形的面积问题”“变速直线运动的路程问题”都是定积分的现实原型，抽象得到的定积分定义后，数学家们辛勤探索得到定积分的性质、定理、公式等，理论完善后再应用现实原型中。整个过程中有抽象之美、演绎推理之美、空间想象之美、应用之美等。定积分在微积分中是需要花时间讲清楚的概念，其严格定义简述如下[4]：

其中f(x)称为被积函数,f(x)dx称为被积表达式,x称为积分变量,[a,b]称为积分区间。

由于对于任意的分法结果一样，可等分区间得：

近似公式为：

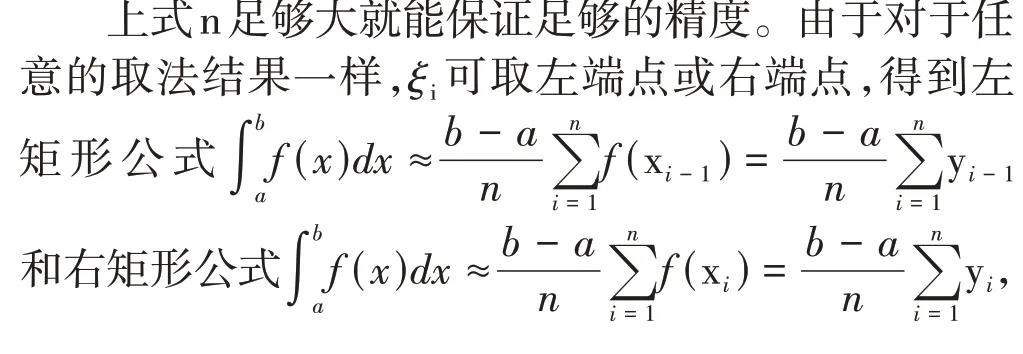
解：注意到该实例属于“积不出来”的积分，无法用牛顿—莱布尼茨公式得到结果，只能考虑利用计算机进行近似计算。将区间[0,1]进行十等分，设分点为xi(i= 0,1,...,10),设其相应的函数值为：yi=e-x2i(i=0,1,...,10),列出表格如表1[5]。

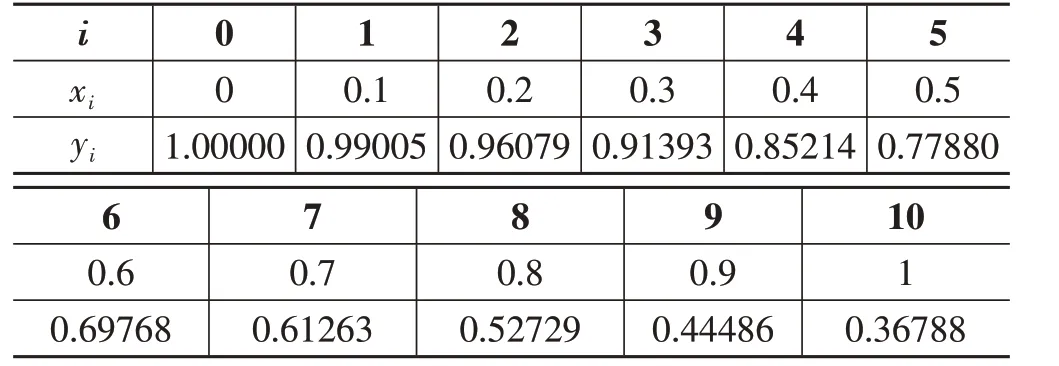
表1 等分点函数值表

根据左矩形公式，计算得：

根据右矩形公式，计算得：

根据梯形公式，计算得：

由梯形公式得到的结果实际是前面两个值的平均值。

该实例算法的伪代码表示如下[6]：

1)定义常量n=10，这里的n代表对区间n等分。

2) 定义有n+1 个分量的数组X，其分量为X[0],X[1],X[2]...X[n]。

定义有n+1个分量的数组Y，其分量为Y[0],Y[1],Y[2]...Y[n]。

利用y[i]=e-x2[i],i= 0,1,2...n对数组Y循环赋值。

4) 根据左矩形公式，通过循环实现累加求和得到S1；

根据右矩形公式，通过循环实现累加求和得到S2；

根据梯形公式，通过循环实现累加求和得到S3。

5)输出S1，S2，S3。

综上所述结论是：微积分就是一个大算法，是一系列演算法则的集合。