基于贝叶斯优化的支持向量回归模型对电能表在线率的预测

余俊泽，夏显威，雷春俊，赵冬立，马群，陈百龄

(塔里木油田公司 a.新能源事业部；b.油气生产技术部，新疆 库尔勒 841000)

电能表作为电力系统中至关重要的计量设备[1]，通常用于核定用户用电量并进行经济核算[2]。随着社会进步和科技发展，数字式电能表已逐渐取代传统的机械式电能表[3-5]。

在这一背景下，电能表的在线率成为衡量实时数据采集成功率的关键指标，对于保障整个电力系统的稳定运行具有重要意义。电能表的高在线率对电力企业进行负荷预测、电力调度和资源优化等关键决策具有重要价值，挖掘与电能表在线率相关的数据并预测其变化趋势现已成为一项关键任务[6]。为实现这一目标，尝试通过支持向量回归(support vector regression，SVR)算法——一种广泛应用于回归分析和预测的机器学习方法[7-8]来进行电能表在线率的预测，但是该算法易受过拟合的影响，预测性能差[9-11]。

贝叶斯优化方法[12]可有效解决这一问题。它通过定义先验概率分布，融合不确定信息和专家知识，保证了模型的泛化能力。同时，贝叶斯优化可以自动调整模型的超参数[13]，避免手工调参经验性强、不准确的问题，进而寻找到全局最优解[14-16]。于是，将贝叶斯优化[17]引入SVR模型中，期望通过贝叶斯方法自动优化SVR模型中的重要超参数(如惩罚参数C和核函数参数γ)，从而找到全局最优参数组合，最大限度地发挥模型的效果[18-19]。

类似的智能优化思路还有很多。例如：文献[20]提出一种主蒸汽压力的优化方法，该方法首先使用聚类算法对数据进行预处理，提取关键特征，然后采用SVR进行建模和优化，可有效提高主蒸汽压力预测的准确性；文献[21]提出一种锂电池健康状态预测方法，该方法利用遗传算法对SVR模型的参数进行优化，可提高模型的泛化能力和预测精度，为电池健康管理提供有力支持；文献[22]提出一种短期电力负荷区间预测方法，该方法采用多目标优化策略平衡预测精度和计算复杂度，并利用贝叶斯优化技术自动调整模型参数，可实现短期电力负荷预测的优化。

这些智能优化方法充分展现了机器学习和优化算法在实际生产生活中的巨大潜力。通过整合多种方法，可以进一步提升预测模型的性能，从而为实际应用创造更多价值。

然而，在前述研究中，少有人关注多维度数据的收集以及关键变量的筛选。本研究针对电能表在线数等24个变量展开了深入研究，并运用反向特征消除(reverse feature elimination，RFE)方法进行数据降维，成功筛选出影响电能表在线率的5个主要变量。借助这种方法，可以更有效地预测电能表的在线状态。

以塔里木油田电网为例，不稳定的电能表在线率会对实际生产生活产生较大影响。为此根据各作业区的电能表实际在线表计数、无信号表计数、停用表计数等变量，筛选出影响电能表在线率的主要因素，并将其应用于电能表在线率的预测，这对于保障油田生产用电计划具有重要参考价值。

鉴于此，将整个数据分析过程划分为3个部分：第1部分为数据预处理；第2部分为运用RFE方法进行数据降维；第3部分为运用基于贝叶斯优化的SVR方法完成对电能表在线率的预测。

1 模型使用数据

1.1 数据概况

本研究所使用数据来源于电能表在线统计后台，数据的起止时间为2022年3月5日—2023年4月2日，数据包括系统总计电能表在线数、理论在线电能表数、实际在线电能表数、各地区电能表在线数、需确认现场表计数、停用表计数、无信号表计数、校验表计数、虚拟表计数、终止用户表计数、信号弱表计数、表计上线率等共24个变量。

1.2 数据预处理

因存在原始数据部分数据缺失且个别数据出现较大波动的情况，本研究先进行数值填充及异常值剔除。

1.2.1 数据填充和平滑

为简化插值计算并确保一定的插值精度，本文在多种方法中选择了线性插值方法来填充缺失数据。线性插值的优势在于其计算简单、易于理解。与其他复杂的插值方法(如三次样条插值或高阶多项式插值)相比，线性插值的计算速度更快，且在实际应用中的误差范围通常可以接受；因此，选择线性插值方法可以在保持计算效率的同时，满足相应的精度需求。

此外，本研究采用移动平均法来消除原始数据中存在的随机波动。移动平均法是常用的时间序列分析方法，通过计算一定时间范围内的数据平均值来平滑数据波动，从而使数据更加稳定。相较于其他平滑方法(如指数平滑法)，移动平均法的优势主要体现在简单易懂、计算过程透明2个方面。而且，移动平均法在处理具有周期性和趋势性的数据时表现尤为出色，有助于揭示数据潜在的规律。

综上所述，本研究选择线性插值方法和移动平均法相结合的方法来完成数据预处理，进而在保证保留原始数据精度的同时，消除原始数据中的随机波动。

1.2.2 异常数据的剔除

箱型图主要通过计算上下边缘﹝即上下四分位数加、减1.5倍的四分位距(interquartile range，IQR)﹞来确定数据的正常范围，超出这个范围的数据点会被标记为异常数据。通过清洗和修正异常数据，可以提高后续分析和建模的准确性。

箱型图如图1所示：除变量3、变量15箱体较长，其余变量的箱体都呈现出较短的特征；总体而言，各变量分布集中，除变量15的中位数靠近下四分位数外，其余变量的中位数普遍靠近上四分位数，数据整体体现出右偏分布。综上所述，数据整体数值较大，集中程度较高，但存在部分异常值(图中红色十字形标记)，需要进一步处理。

图1 平滑处理后数据的箱型图Fig.1 Box plot of the data after smoothing treatment

进一步，本文采取IQR方法来确定异常值。具体原理如下：

首先，计算数据集的下四分位数Q1和上四分位数Q3。四分位数将数据集分为四等份。对于Q1，有25%的数据低于该值；对于Q3，有75%的数据低于该值。

计算IQR，即Q3与Q1之间的差值

kIQR=Q3-Q1.

(1)

计算异常值的阈值：

BL=Q1-1.5kIQR，

(2)

BU=Q3+1.5kIQR.

(3)

式(2)、(3)中：BL为下界；BU为上界；1.5为常用系数，用于确定异常值范围。

对于数据集中的每个数据点，如果其小于下界或大于上界，那么就被认为是异常值。

2 数据降维

常用的数据降维方法包括主成分分析(principal components analysis，PCA)、线性判别分析(linear discriminate analysis，LDA)和t-分布邻域嵌入(t-distributed stochastic neighbor embedding，t-SNE)算法。其中：PCA通过线性变换将原始特征空间映射到新的低维特征空间，最大化地保留数据的方差，该方法适用于无监督学习场景；LDA同样采用线性变换，但该方法关注于类别间的分离度最大化，适用于有监督学习场景。

PCA方法可降低数据维度；但该方法包含自变量和应变量，属于监督学习任务，因此PCA不是最佳的降维方法。LDA方法可降低的维度有限，对于模型的简化效果并不好；因此其需要模型具有较强的线性关系。

2.1 数据说明

由于系统共计电能表在线数、理论在线电能表数、实际在线电能表数为相应变量相加所得，不存在独立性，因此需先去除。后续均根据剔除此3个自变量后的数据继续分析。

2.2 变量的相关系数矩阵

为直观地展示数据集中各个变量之间的线性相关性，更好地理解数据集中各个变量之间的关系，本研究对表1所示的20个自变量绘制相关系数矩阵点图，如图2所示。

表1 待进行数据降维的变量Tab.1 Variables awaiting dimensionality reduction

图2 20个自变量的相关系数矩阵点图Fig.2 Scatter plot matrix of correlation coefficients for 20 independent variables

由图2可知，变量的相关系数矩阵点图的左上侧和右下侧多为红色，而左下侧和右上侧的颜色多为蓝色。这种现象意味着数据集中存在2个或多个变量子集，子集内部的变量之间具有较强的正相关性，而不同子集之间的变量呈现负相关性。在实际分析过程中，需要关注高度相关的变量，因为它们具有多重共线性，会影响回归模型的稳定性和可解释性。

结合以上思考，需要先判断模型是否属于复杂的非线性问题，这一步主要通过残差分析进行。

2.3 残差分析

残差分析是评估回归模型拟合效果和确定模型是否线性的方法。在残差分析中，判断模型是否线性可以依据残差的随机分布：如果模型是线性的，那么残差应该在整个自变量范围内呈现随机分布，没有明显的规律。通常可以通过绘制残差散点图来观察残差的分布情况，如图3所示。

由图3可知，残差散点图的散点主要集中于图像下侧，且在[-0.001 5，0.001 5]区间内随机分布，这说明残差在这个区间内没有明显的偏差。但对于残差的分布是否具有正态性，需要进一步的检验。可通过绘制如图4所示的残差QQ图(residual quantile-quantile plot)来检验模型残差是否近似服从正态分布。如果残差呈现正态分布的话，QQ图上的点大多会落在45°线上。

图4 残差QQ图Fig.4 Residual quantile-quantile plot

由图4可知，残差QQ图的数据点基本沿同一条直线分布，但尾端数据点明显偏离直线，这说明模型不符合正态分布的假设。进一步比较正态分布与残差分布，绘制如图5所示正态分布残差直方图，通过观察图像的偏度情况，来评估回归模型拟合的结果。

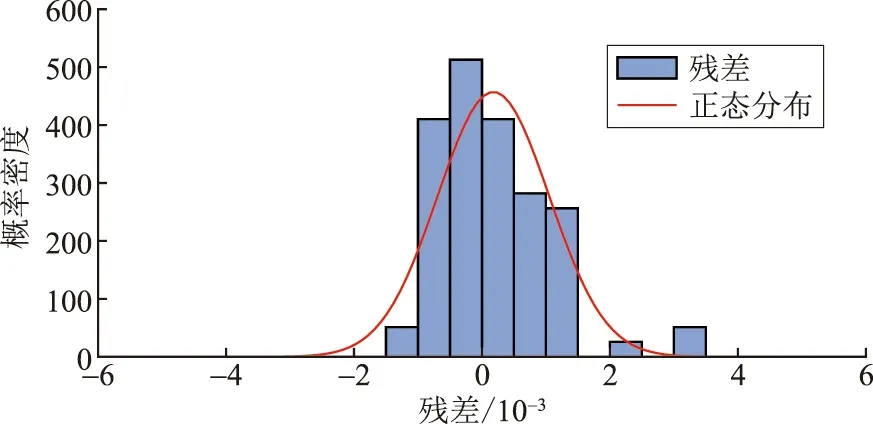
图5 正态分布残差直方图Fig.5 Histogram of normally distributed residuals

由图5可知，直方图形状偏离正态分布，表明残差不符合正态性假设。

综上所述，尝试建立简单的线性回归模型来解释应变量随自变量的变化，是不满足正态性假设的，线性模型不具有稳定性和可靠性，电能表在线率的预测问题属于非线性问题。

2.4 基于RFE方法进行数据降维

特征选择方法的目标是在保留原始特征可解释性的同时，选择对模型预测贡献最大的特征子集。通常在处理非线性问题时，特征选择方法比线性降维方法更具优势。RFE是一种用于特征选择的降维方法，其基本原理是使用1个模型进行多轮训练，每轮训练后移除一部分特征，然后重新训练模型，最终选择表现最佳的特征子集。RFE方法的详细步骤如下：

步骤1，设置自变量矩阵和应变量矩阵；

步骤2，设置RFE的参数(选择特征数量为5，每次迭代时移除1个特征)；

步骤3，判定当前选择的特征数量是否小于5；

步骤4，使用当前特征集训练1个线性回归基础模型；

步骤5，获得回归系数的绝对值；

步骤6，从特征集中移除具有最小系数的特征；

步骤7，更新当前特征数量，返回步骤2。

经过筛选，得到降维后的变量见表2，表中回归系数较小是由于自变量和因变量的绝对值偏差较大。

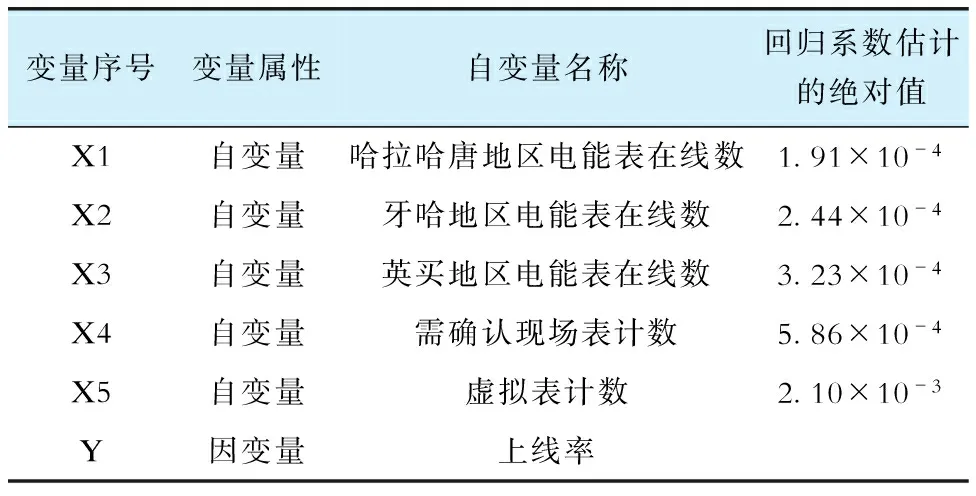
表2 数据降维后得到的各变量Tab.2 Variables obtained after data dimensionality reduction

为反映出各数据的波动情况，将各变量进行归一化处理后绘图，如图6所示。

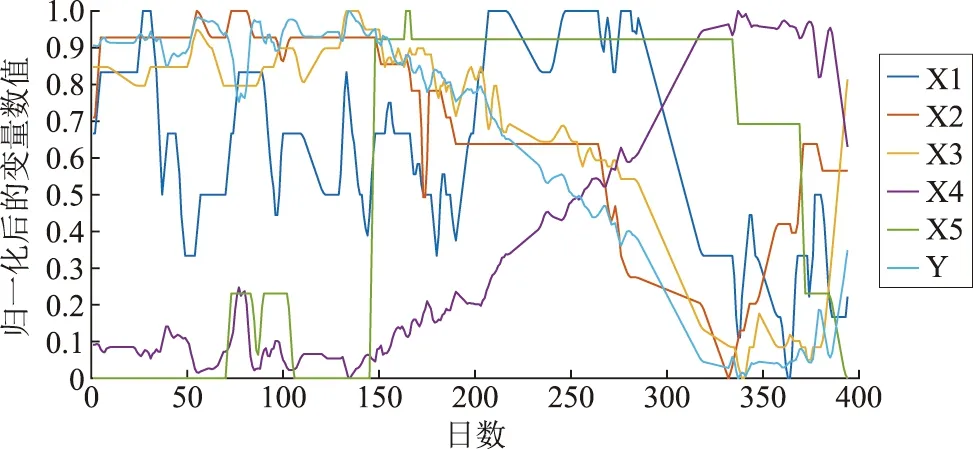
图6 归一化后的降维数据Fig.6 Normalized dimensionality reduction data

由图6可知，序号为X1、X2、X3的自变量数据与因变量之间具有强正相关性，序号为X4、X5的自变量数据与因变量之间具有强负相关性。由此可见，数据降维过程将原始高维的自变量空间转换为较低维度的新空间，可保留数据中的主要结构和信息，减少系统噪声并解决多重共线性问题。

进一步，通过在整体样本上不断重复RFE，以保证变量筛选结果稳定。统计各特征被选中次数及被选中几率见表3，其中N100、N500、N1000分别为重复100、500、1 000次RFE后各特征被选中次数。

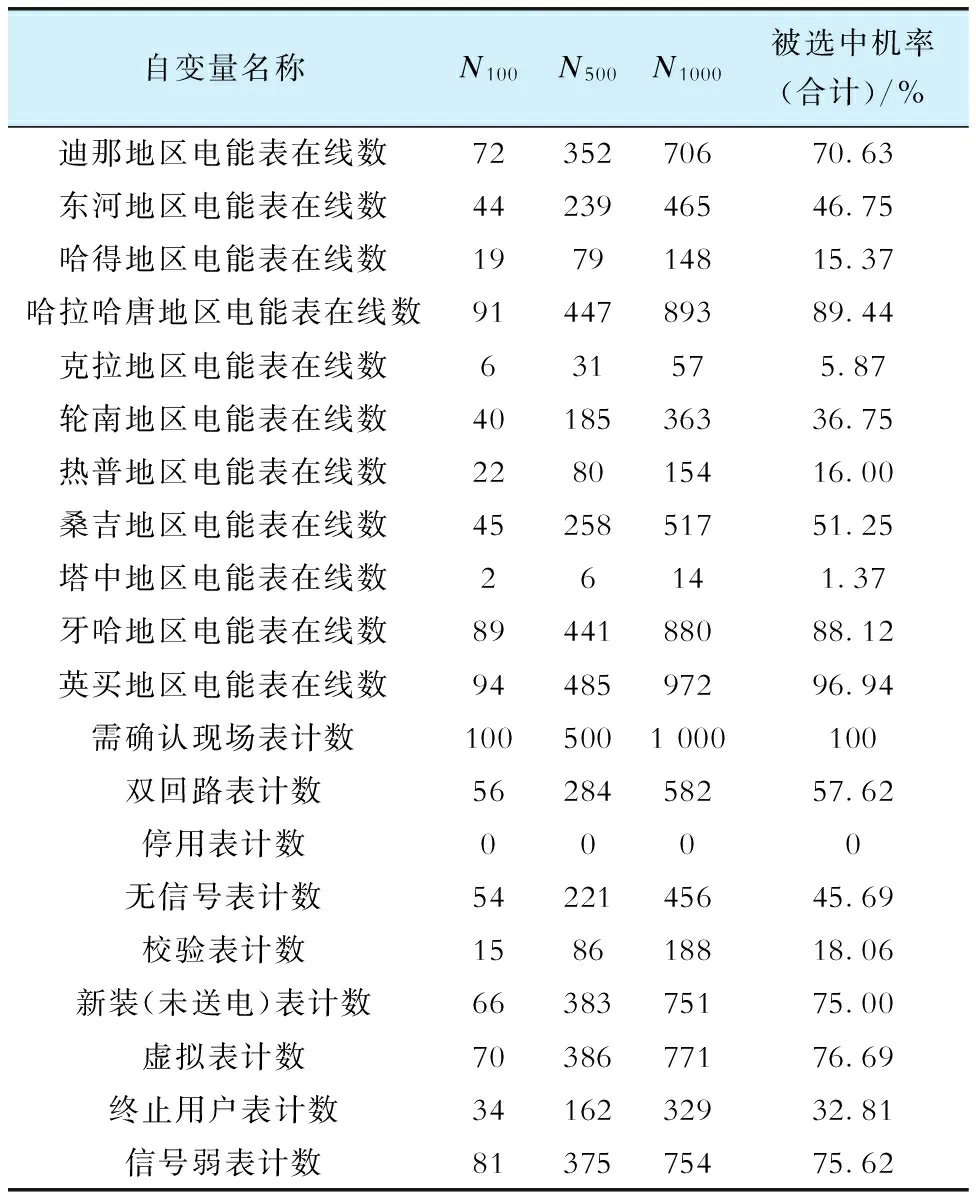
表3 RFE重复试验结果Tab.3 Results of repeated RFE experiments

综上，在结合重复实验并保留5个被选中次数最高的变量的条件下，重复执行RFE得到的最佳特征子集与前述结果保持一致。

3 对电能表在线率进行预测

SVR是一种基于支持向量机的回归算法，用于预测连续型目标变量。SVR的主要特点是通过引入ε-insensitive损失函数，使得预测误差在一定范围内的数据点不受惩罚，同时最大化间隔以提高模型的泛化能力。SVR可应用于线性和非线性回归问题，通过使用核函数(如径向基函数、多项式核等)将原始特征映射到高维空间，从而实现对非线性关系的建模。SVR在处理具有高维特征、非线性关系和噪声较多的数据集时具有较强的鲁棒性。

贝叶斯优化是一种基于概率模型的全局优化算法。它使用高斯过程回归来拟合目标函数(ε-insensitive损失函数)，寻找得到最佳参数。贝叶斯优化的主要优势在于仅需要较少的迭代次数，就能找到全局最优解。

对于电能表在线率预测问题，将数据集(自变量和因变量)划分为训练集和测试集2个部分，使用贝叶斯优化方法计算k折交叉模型的损失，以优化正则化参数C以及径向基核函数尺度参数γ2种超参数，进而获得稳定的模型泛化能力。具体步骤如下：

步骤1，划分训练集和测试集(采用70%数据的训练集、30%数据的测试集)；

步骤2，定义要搜索的超参数空间(将正则化参数C和径向基核函数尺度参数γ均设置为10-5～105)；

步骤3，使用k折交叉验证评估模型性能(设置k=5)；

步骤4，定义网络搜索的目标函数最小值；

步骤5，使用贝叶斯优化进行网络搜索；

步骤6，获取最佳参数；

步骤7，使用最佳超参数训练SVR模型；

步骤8，使用测试集评估性能；

步骤9，输出均方误差。

算法执行流程如图7所示。

图7 算法执行流程Fig.7 Algorithm execution flowchart

运行模型后，得到模型运算的结果见表4，其中结果评价可分为最佳和可接受2种结果。表4中：“最佳”表示目标函数返回的有限值低于先前计算的目标函数值；“可接受”则表示目标函数返回有限值；目标函数值中第1列所示的“观测值”表示计算的最小目标函数值，此值取当前或迭代的目标函数最小值；而第2列的“估计值”则表示在每次迭代中，软件使用更新后的高斯过程模型，根据当前尝试的所有超参数集估计目标函数值的置信边界上限，然后，软件选择具有最小置信边界上限的点，该值即对应达到该条件后所返回的目标函数值；最右侧2列数值即目标函数所对应的正则化参数C和径向基核函数尺度参数γ。

表4 贝叶斯优化的过程及得到的最优超参数组合Tab.4 The process of Bayesian optimization and the optimal hyperparameter combination obtained

在运行模型后，挑选根据最终高斯过程模型在最终迭代中产生的最佳目标函数估计值对应的超参数集作为最佳超参数组合，见表5。

表5 最佳超参数组合Tab.5 The best hyperparameter combination

根据上述内容，传递SVR模型相关参数如下：采用高斯核函数，设置目标函数ε-insensitive中的ε=0.016，间隙容忍度为1.0×10-3，正则化参数C=4.204，核函数尺度参数γ=10.249。

通过训练模型得到的支持向量见表6。

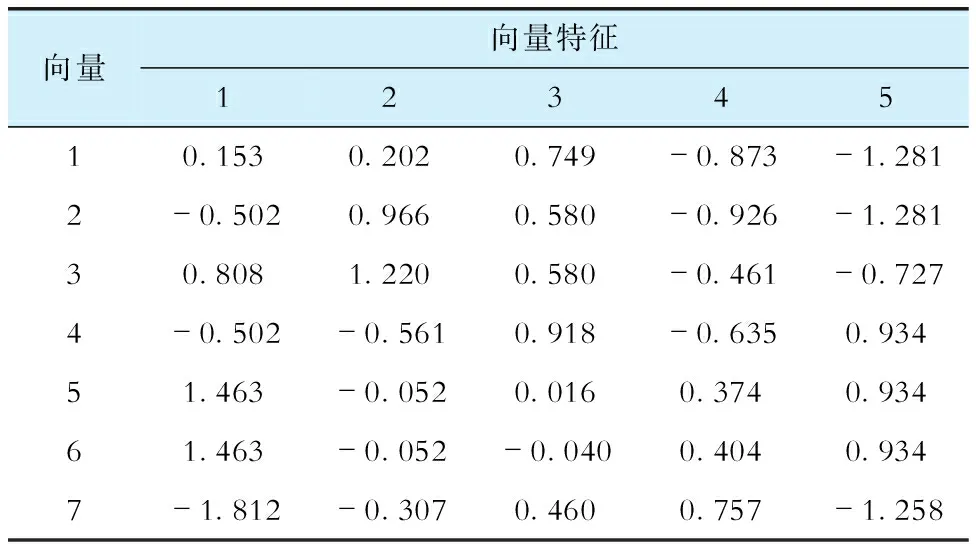
表6 支持向量一览Tab.6 List of support vectors

图8展示了优化过程中目标函数最小值随着迭代次数的变化情况，优化算法在20次计算内成功地将目标函数值显著降低。这表明优化算法在这个问题上的收敛速度较快。在20次计算后，目标函数值接近0，这意味着模型的泛化能力较好，预测误差较小。

图8 最小目标值关于函数计算次数图像Fig.8 The minimum target value with respect to the number of function calculation image

估计的目标函数值随正则化参数C和径向基核函数尺度参数γ这2种超参数变化情况如图9所示，图像呈漏斗状，漏斗状的图像表明，超参数接近最佳组合。

图9 估计的目标函数值随2种超参数变化的情况Fig.9 Variation of the estimated objective function values with two hyperparameters

本研究将贝叶斯优化的SVR算法同随机森林算法、梯度提升算法、SVR算法、K最邻近算法进行比较，绘制各算法预测结果曲线，如图10所示。

图10 各算法预测结果曲线Fig.10 Comparison image of prediction results from various algorithms

进一步使用加权平均绝对误差指标EWMAE和均方差指标EMSE对模型预测结果进行评价，并统计各算法预测结果对应的EWMAE和EMSE，见表7。

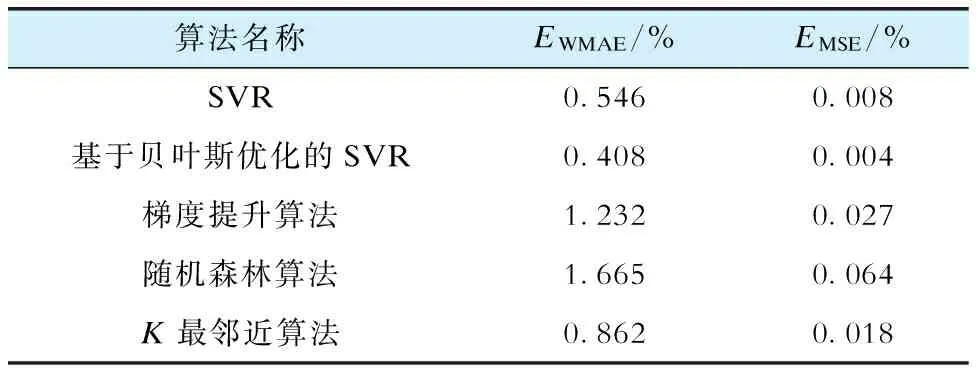
表7 各算法对应的加权平均绝对误差和均方差Tab.7 Weighted average absolute error and mean square deviation corresponding to each algorithm

(4)

(5)

式(4)、(5)中：n为样本个数；yci为预测值；yi为实际值。

计算得到贝叶斯优化的SVR算法预测结果对应EWMAE为0.408%，EMSE为0.004%，模型在预测任务上具有较好的性能，误差较小。

4 结束语

通过使用贝叶斯优化下的SVR方法，可高效且准确地预测电能表的在线率。贝叶斯优化技术有助于在超参数空间中找到最佳组合，从而提高了模型的预测性能。与其他传统方法相比，这种方法计算时间较短，使得模型能够在有限的时间内快速获得高质量的预测结果。同时，预测误差较小，表明模型在预测电能表在线率方面具有较好的准确性和鲁棒性。综上所述，贝叶斯优化下的SVR方法在电能表在线率预测任务中表现出色，具有实际应用价值。