灵动的数学条件

文／江苏省太仓市荣文中学 肖文轩

解决一个数学问题，其思考方式大致分为按条件思考或者依结论倒推。当两者在思维上碰撞时，那么问题就迎刃而解了。

例题在△ABC中，已知AC=BC，∠ACB=90°，点D是AB的中点，点E是边AB上一点，连接CE。

（1）直线BF垂直于CE，垂足为点F，交CD于点G（如图1），求证：AE=CG；

图1

（2）直线AH垂直于CE的延长线，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并加以证明。

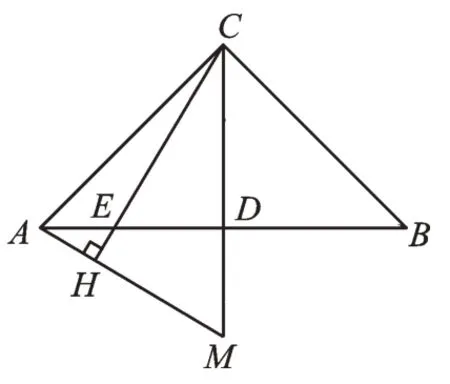
图2

按照做题思路，我们先分析条件：①AC=BC；②∠ACB=90°；③点D是AB的中点。一共有三个条件，单个条件能得到一些结论，两两结合能得出更奇妙的结论。例如，①②结合，可得∠CAB=∠CBA=45°……

问题（1），提供了条件④BF⊥CE，②④结合可得∠ACE=∠CBF。以上都是根据条件向下推理得出的。依据结论AE=CG，说明要证明△CAE≅△BCG，再根据条件得出的结论，两者在此“胜利会师”，问题得解。

问题（2）首先要进行数学猜想：BE=CM，从而要证明△CBE≅△ACM。我发现，还缺少相等的条件，由条件⑤AH⊥CH，同样和②结合，得出∠CAH=∠BCE，思维的结合点在这里，题目得到完美解决。

对于难度较高的题目，我们要形成一种好的思维习惯。首先通过题目，理解每一句，独自推理每一句的几何语言，然后几个条件一起进行推理，推断出一些相应的结论，再从结论出发反推，最后形成一连串合理的推断。

教师点评：

小作者通过自身的解题过程，总结出自己的解题思路，形成了解决几何问题的思想方法，充分地利用条件、分析条件，进行合理的推断，再从结论反推，架起解决问题的“桥梁”。小作者勤于思考、反思、总结，形成解题体系，这是我们提高思维水平的重要途径。