推力空气箔片轴承新型结构构建及其动力学性能

王 旭， 许浩杰， 邵聪鹏， 安 琦

（华东理工大学机械与动力工程学院, 上海 200237）

推力箔片轴承具有高效、清洁、无油等优点，特别适用于低负载、高功率密度的旋转机械，目前引起世界范围重视的燃料电池的高速空压机转子，就需要用到这种轴承。氢燃料电池空压机转子的转速一般都在100 000 r/min 以上，不仅需要推力空气箔片轴承有良好的静特性，对于其动特性要求也很高。

郭志阳[1]通过实验以及理论分析整体式气体箔片轴承的非线性承载力的形成机理，在考虑箔片结构、轴承润滑气膜和转子结构的条件下通过耦合转子动力学和瞬态动力学建立了完整的动力学求解模型。文献[2-4]针对鼓泡型箔片轴承进行研究分析，该鼓泡型结构箔片轴承由于鼓泡结构分布不均匀会对轴承的动力学性能造成影响。叠片式箔片轴承是多层箔片结构组成的，由于结构复杂造成安装困难，同时复杂的结构对箔片造成额外的载荷[5-7]。宋国强等[8-9]在考虑稀薄气体效应条件下对弹性材料支撑型箔片轴承进行轴承性能研究。闫佳佳等[10-11]研究了轴承结构参数、间隙参数、涡动频率和转子转速等对推力箔片轴承的动力学特性系数的影响规律。罗轶欣等[12]在引入黏性耗散项的条件下探讨了结构参数对气膜温度的影响。乔湘云等[13]以整体式箔片轴承为对象研究了轴承结构参数和转速对推力箔片轴承气膜压力和气膜温度的影响规律，但整体式箔片轴承安装完成之后动力学性能无法进行刚度调节。南国栋[14]联合三维气膜能量方程和非等温Reynolds 方程进行耦合求解，得到推力箔片轴承气膜温度分布、气膜压力分布，并分析了推力箔片轴承载荷与转速对气膜温度的影响规律。

目前箔片轴承的结构形式比较多，但都存在着一定的不足，无法对箔片进行调整从而改变轴承的刚度等动力学性能。针对这一问题，作者提出一种新型推力箔片轴承结构[15]，该新型轴承的特点是平箔和波箔进行组合为顶箔提供支撑，并且取消传统的点焊固定，采用箔片的L 型端部和轴承基座径向槽配合的方式进行固定，该轴承既解决了箔片无法改变刚度的问题，又解决了点焊给箔片增加额外载荷的问题。本文针对这一新型结构的推力空气箔片轴承开展力学分析，建立推力箔片轴承的动力学性能模型，研究各种因素对其动力学性能的影响规律。

1 箔片轴承结构及原理分析

通过运用流体润滑创新构建了一种由顶箔、波箔、平箔、基座等组成的新型推力箔片轴承，结构如图1 所示。

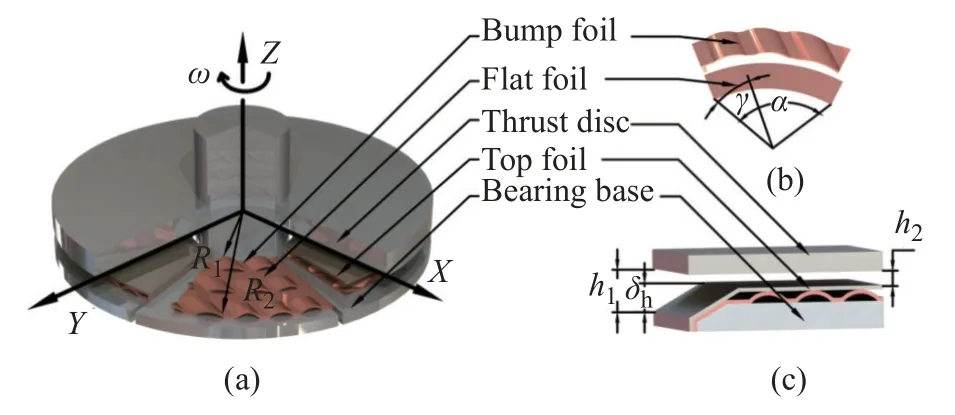
图1 推力箔片轴承结构示意图Fig.1 Schematic diagram of the thrust foil bearing structure

该新型推力箔片轴承的特点是采用组合式波箔，这种结构可以实现对轴向刚度的调节，从而改变整个推力箔片轴承的动态特性，实现对所支撑的转子动力学的性能优化。图1 中R1为轴承内径；R2为轴承外径；α为扇形箔片的张角，定义B为节距比(B=γ/α)；δh为楔形间隙出入口高度差；h1为楔形间隙入口高度；h2为楔形间隙出口高度；ω为角速度。

2 理论建模

2.1 能量方程

对推力箔片轴承进行热特性分析。气膜的温度对气体的黏度和密度均有影响，在柱坐标系下，推力箔片轴承稳态气膜能量方程为[13]：

式中：ρ为气体密度；cp为气体定压比热容；κ为气体导热系数；vr为气体径向流速；vθ为气体周向流速；T为气膜温度；r为半径方向坐标；θ为圆周方向坐标；z为气膜厚度方向坐标；P为气膜压力；μ为空气动力黏度。

μ是T的函数，可通过黏温方程[16]来表示：

式中：a=4×10-8；Tref=-185.6 K。

通过设置量纲为一参数联立式(1)～式(3)，得到量纲为一方程：

2.2 箔片变形分析

推力轴承6 块扇形瓦块均匀分布在基座上，因此在推力盘无倾斜条件下采用弹性力学分析其中一片箔片的变形，就可以得到整个推力轴承的箔片变形，箔片变形示意图如图2(a)所示，在载荷作用下，顶箔和波箔均发生变形，tT是顶箔厚度。如图2(b)所示，波箔具有波拱形结构，其中l是半波拱宽度，s是全波拱宽度，R0是波拱半径，φ是波拱半角，Rr是波拱圆角半径，tB是波箔厚度。如图2(c)所示，在载荷作用下波箔发生变形，假设波箔所受载荷作为集中力F作用于波拱的波峰，则波拱的波峰在水平方向上的位移是Δx，在垂直方向上的位移是Δy，其水平方向上的位移Δx相较于垂直方向上的位移Δy十分微小，水平方向上的位移Δx可以忽略不计，因此分析顶箔变形时不考虑波箔水平方向上的位移造成的影响[17]。

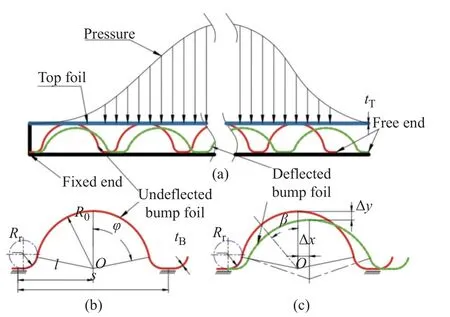
图2 箔片结构变形示意图Fig.2 Schematic diagram of the deformation of the foil structure

用IB代表单个波拱截面的惯性矩，E为弹性模量，Δy表示为：

顶箔结构变形示意图见图3，顶箔的变形w(x)可以分为两部分，波箔变形造成的顶箔在垂直方向上的变形wA(x)，以及自身弯曲变形wB(x)。顶箔由于波箔变形造成的垂直方向上的变形可以表示为：

将顶箔视为二维梁，两波拱之间的顶箔由于弯曲变形，公式不予推导直接给出[18]：

顶箔的整体变形方程可以表示为：

2.3 气膜厚度方程的求解

分析楔形间隙可以得到气膜厚度方程，为计算简便，忽略温度给气膜厚度带来的变化，因此气膜厚度方程可以分为3 个部分[19]：第1 部分为楔形间隙减小部分 (g(θ)) ；第2 部分是楔形间隙保持部分 (h2) ；第3 部分是由于箔片变形造成的气膜厚度的改变(w(r,θ))，因此考虑箔片变形时推力箔片轴承的气膜厚度方程可表示为：

式中：

其中θ与α均为与角度相关的标量。

2.4 非等温Reynolds 方程分析

推力箔片轴承与推力盘之间在一定的转速下会形成相对稳定的具有一定厚度的气膜，在柱坐标系下建立考虑温度变化条件的非等温Reynolds 方程：

式中：h为气膜厚度；t为时间。

通过设置量纲为一参数对式(11)进行量纲为一化，得到：

式中：Pa为环境气体压力；v为涡动频率；ζ为涡动频率比；Λ为轴承数。

代入式（11）得

2.5 动压气体推力轴承动特性分析

在转子保持一定转速时，假设推力盘的轴向静止平衡位置为z0，在此条件下给转子一个轴向的微小扰动量Δz，该微小扰动的位移Δz、速度 Δz˙ 、加速度Δz¨，分别将其进行量纲为一化：

将式(15)代入(12)并忽略高阶项可得：

将式(16)～(19)代入式(13)并整理可得：

式(20)为压力定常控制方程，对其进行求解可以得到推力箔片轴承气膜压力、气膜厚度、箔片变形等静态特性参数。

式(21)、(22)均为压力微分控制方程，对其进行求解可以得到推力箔片轴承的轴向刚度和轴向阻尼等动态特性参数。

2.6 边界条件

2.6.1 定常压力控制方程边界条件 推力箔片轴承稳定运转时，扇形瓦块的每个边界均与外界环境接触，因此认为各边界为环境边界条件：

2.6.2 温度边界条件 在气体入口处，高温循环气体与室温吸入气体混合，因此入口处的温度可以表示为[20]：

其中R为气体常数。

推力盘侧和顶箔侧的热平衡方程分别为：

其中：Atop为气体与顶箔接触面积；Adisc为气体与推力盘接触面积；hout为热对流系数；Ra为推力盘热阻；Rb为轴承基座总热阻。

2.6.3 压力微分控制方程边界条件 推力箔片轴承稳定在h0位置，当发生小扰动时，压力微分控制方程的边界条件：

3 推力箔片轴承润滑流场求解

3.1 求解域网格划分

当箔片轴承稳定工作时，推力盘和推力箔片轴承之间形成稳定的气体润滑膜压力，由于6 个扇形箔片内的压力分布和气膜厚度分布均相同，因此，对其中一个扇形瓦块作为求解域进行分析即可[21]，求解域网格划分和差商示意图如图4 所示。对求解域的网格划分如图4(a)和图4(b)所示，分别为r-θ和z-θ方向上的网格划分，其步长分别为:

3.2 特性系数求解表达式

根据求解出的压力分布可以得到推力箔片轴承单个扇形瓦块的承载力，其表达式为：

轴承的轴向刚度公式和轴向阻尼分别为：

4 算法验证

分别选择文献[22]和[13]进行承载力数据和温度数据对比。在相同的结构参数和运行参数条件下，对比结果如图5 所示，表明本文计算结果和文献趋势具有良好的一致性，且偏差均在3%以内，因此认为本文的模型具有可靠性和准确性。

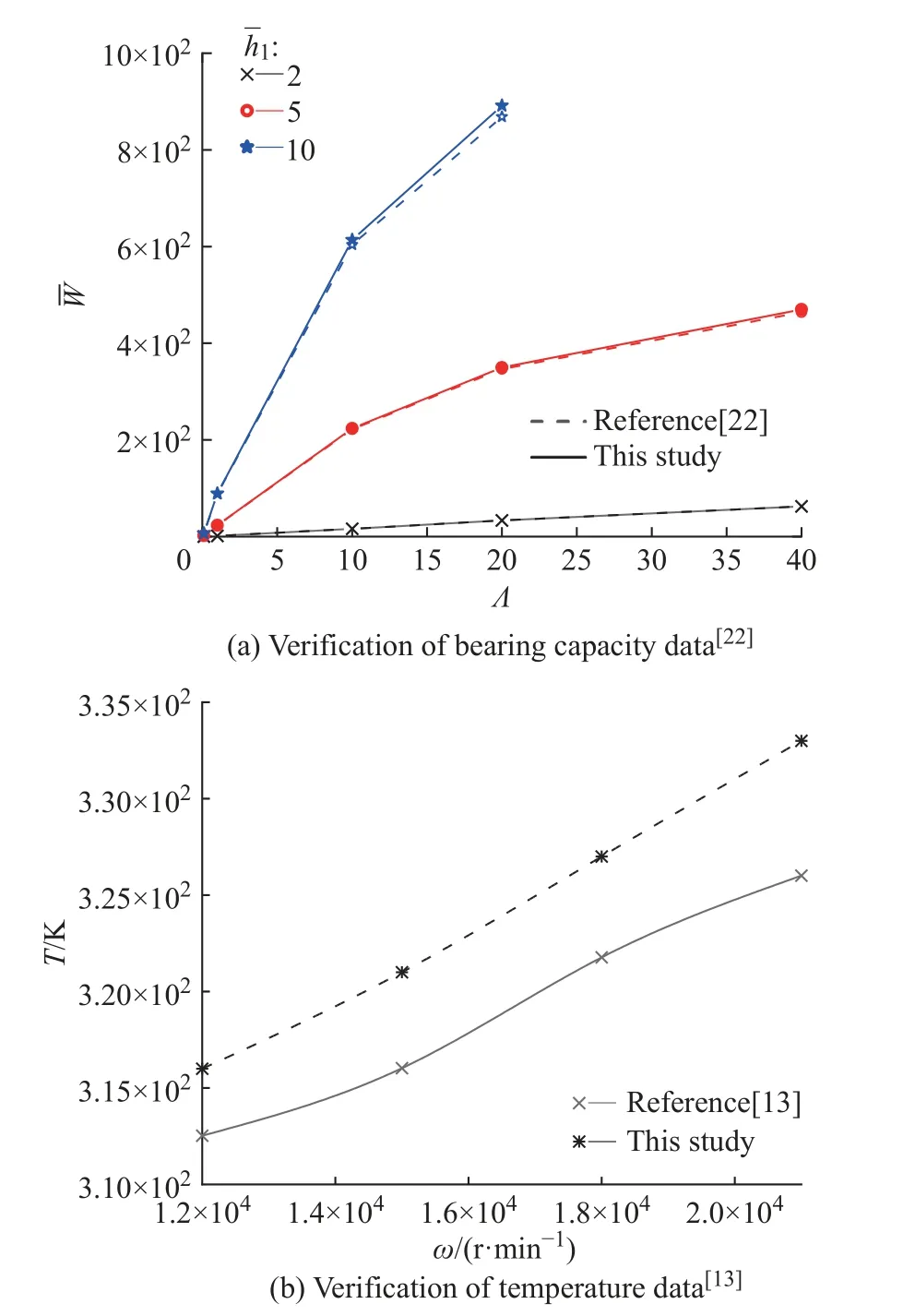
图5 数据验证对比图Fig.5 Data verification comparison chart

表1 所示为推力箔片轴承结构参数和运行参数。

表1 推力箔片部分轴承结构参数和运行参数Table 1 Some structural parameters and operating parameters of thrust foil bearing

5 结果与分析

图6 所示为在本文算例条件下得到的推力箔片轴承的压力分布、气膜厚度分布、顶箔变形量（w）分布、气膜温度场分布。图7～图14 分别示出了波拱半长、楔形间隙高度差、涡动频率、转速、波箔厚度、顶箔厚度、波拱半径、轴承外径对刚度和阻尼的影响。

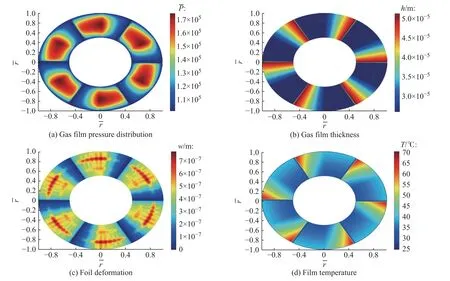
图6 静态参数结果图Fig.6 Static parameter result diagram

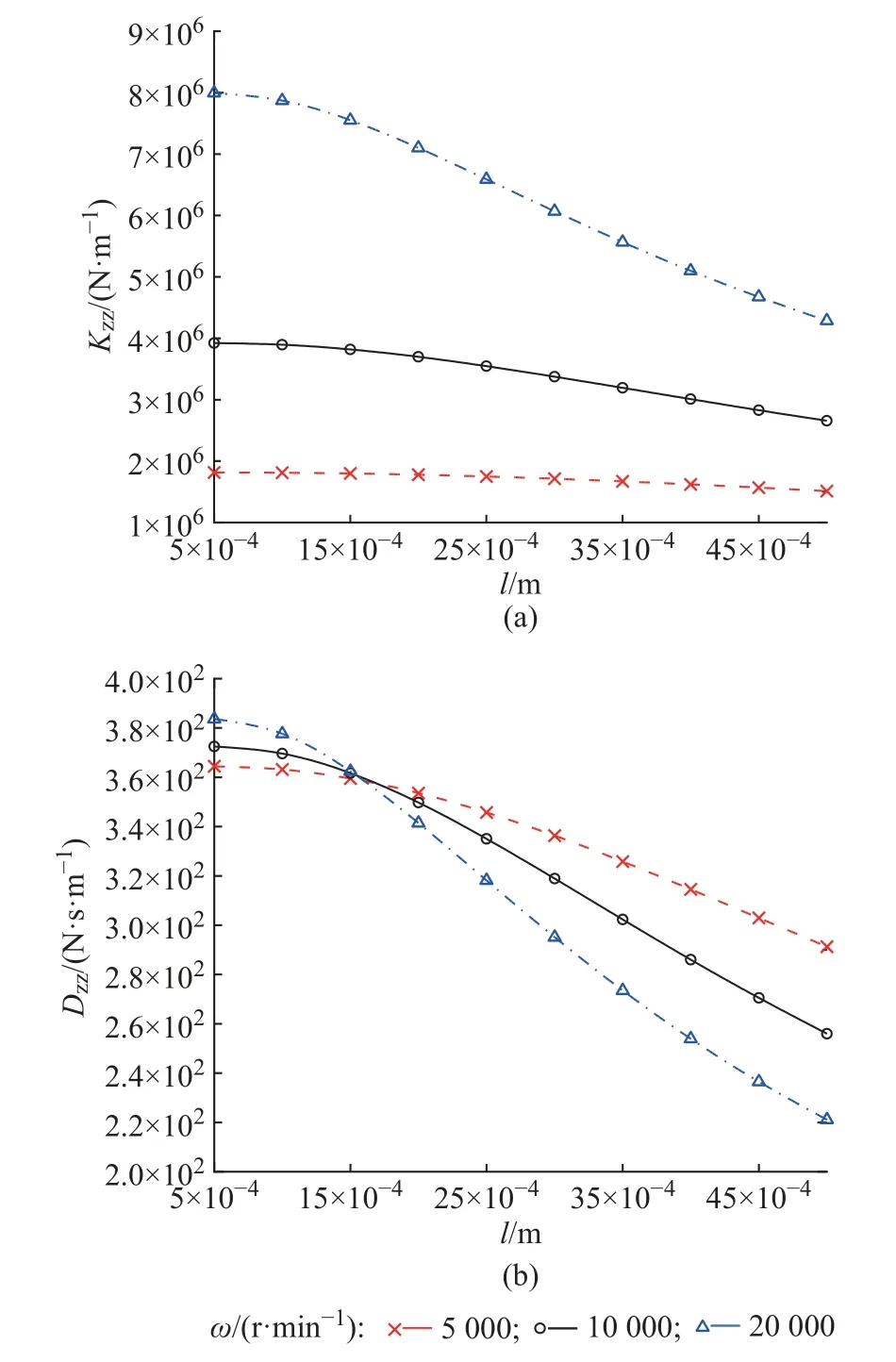
图7 波拱半长对轴向刚度和轴向阻尼的影响Fig.7 Influence of half-length of wave arch on axial stiffness and axial damping

如图7 所示，推力箔片轴承轴向刚度和轴向阻尼随着l的增加而减小，转速越高则减小的趋势越明显。如图8 和图13 所示，推力箔片轴承轴向刚度和轴向阻尼随着δh、R0的增加而缓慢减小，但在此条件下转速对轴向刚度的影响比对轴向阻尼的影响要大。如图9 所示，推力箔片轴承轴向刚度随着ζ的增加而增加，ζ对轴向阻尼的影响不大。如图10 所示，推力箔片轴承轴向刚度和轴向阻尼随着ω的增加而接近线性增加。如图11 和12 所示，推力箔片轴承轴向刚度随着tT、tB的增加有微小的变化，但推力箔片轴承轴向阻尼随着tT、tB的增加具有明显的增加。如图14 所示，推力箔片轴承轴向刚度和轴向阻尼随着R2的增加而增加。

图8 楔形间隙高度差对轴向刚度和轴向阻尼的影响Fig.8 Influence of wedge gap height difference on axial stiffness and axial damping

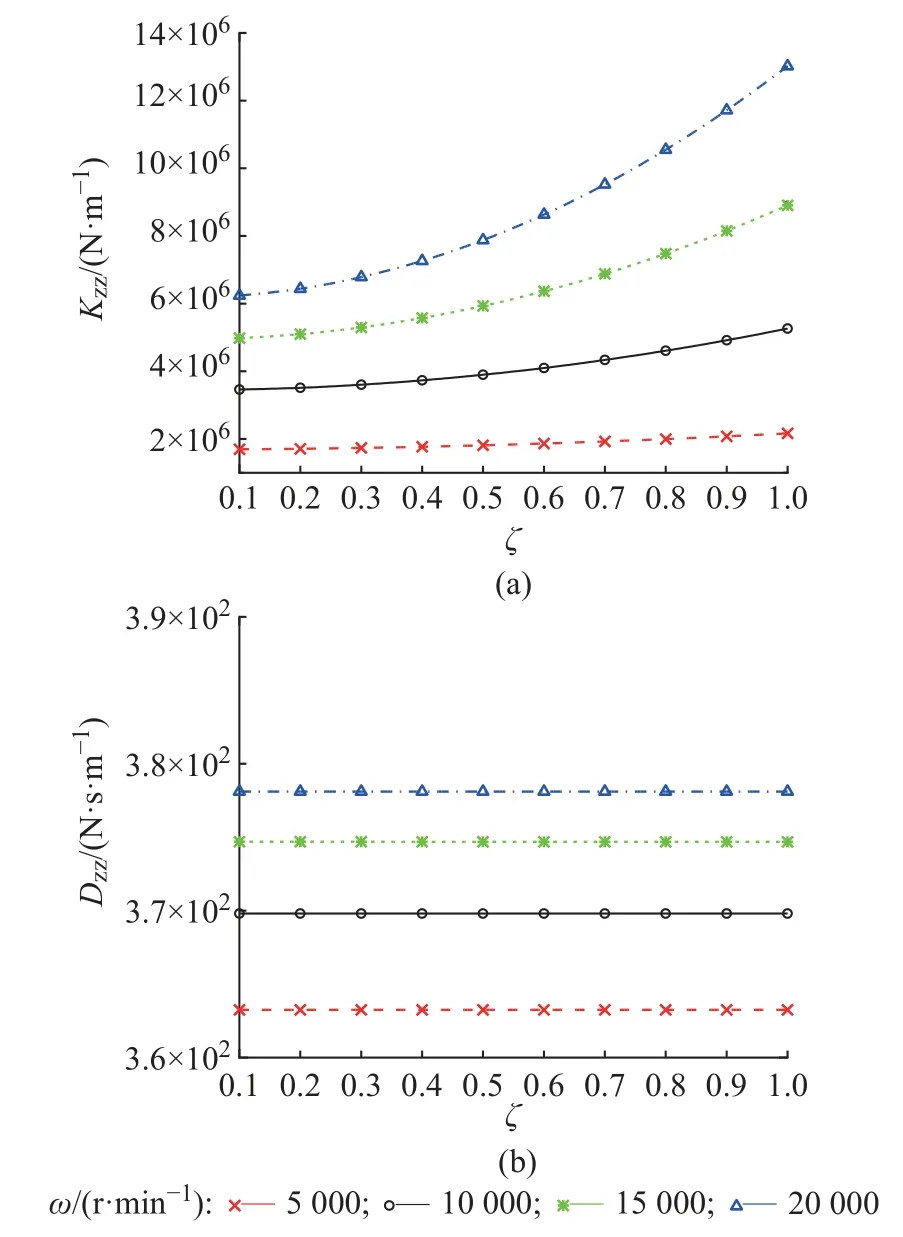
图9 轴向涡动频率比对轴向刚度和轴向阻尼的影响Fig.9 Influence of whirl frequency ratio on axial stiffness and axial damping

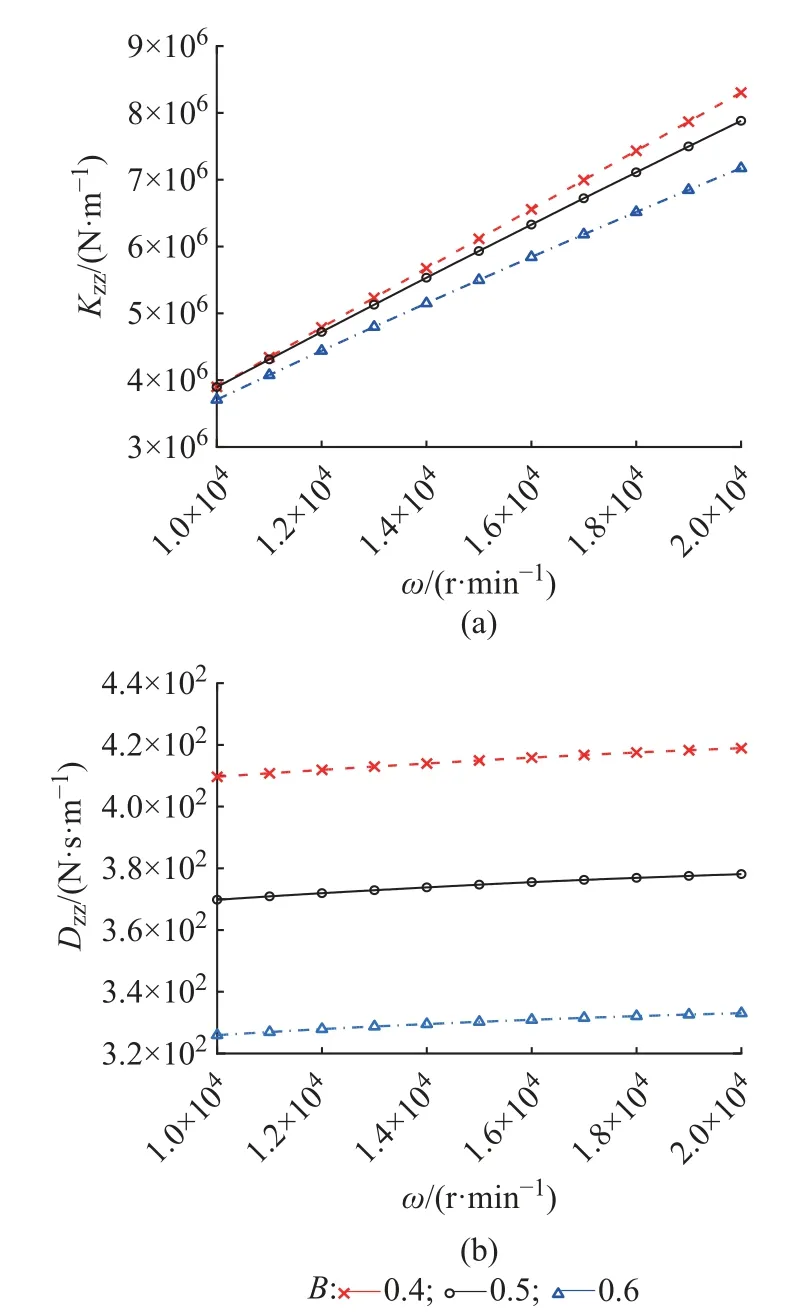
图10 转速对轴向刚度和轴向阻尼的影响Fig.10 Influence of rotational speed on axial stiffness and axial damping

图11 波箔厚度对轴向刚度和轴向阻尼的影响Fig.11 Influence of foil thickness on axial stiffness and axial damping

图12 顶箔厚度对轴向刚度和轴向阻尼的影响Fig.12 Influence of top foil thickness on axial stiffness and axial damping

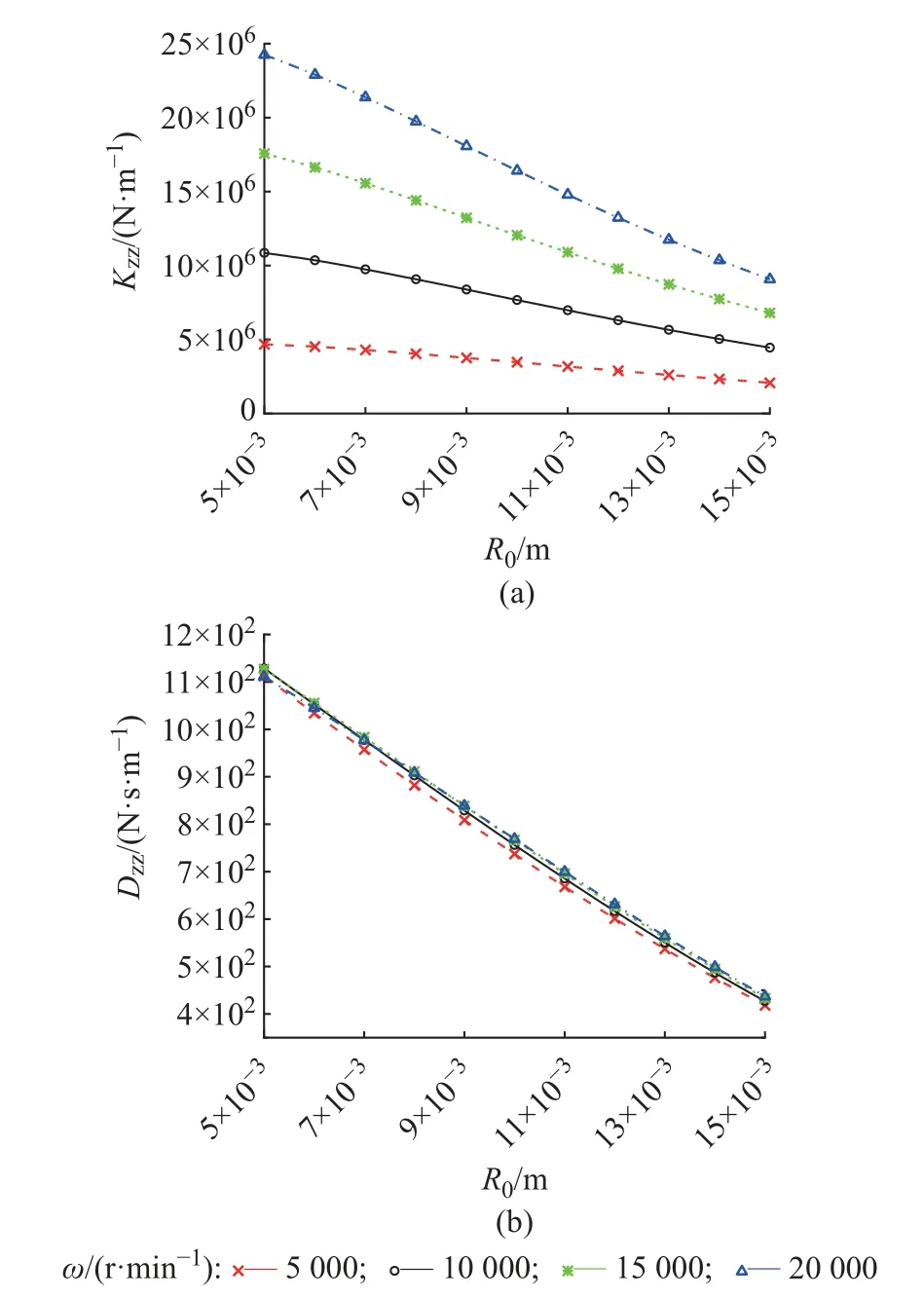
图13 波拱半径对轴向刚度和轴向阻尼的影响Fig.13 Influence of wave arch radius on axial stiffness and axial damping

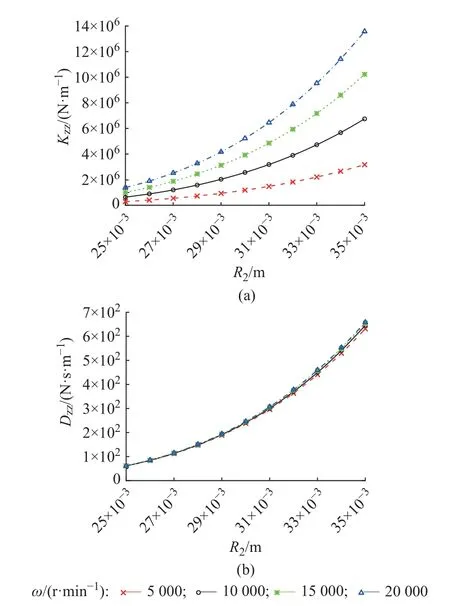
图14 轴承外径对轴向刚度和轴向阻尼的影响Fig.14 Influence of bearing outer diameter on axial stiffness and axial damping

6 结 论

(1)提出一种新型推力箔片轴承结构，该轴承的优点是通过组合平箔和波箔来改变箔片轴承的刚度，从而实现对轴承动力学性能的改变和优化，实现了传统箔片无法实现的功能；其次，箔片的固定方式减少了箔片的额外载荷，箔片处于自然状态时有利于提高箔片轴承的寿命。

(2)针对新型推力箔片轴承进行力学研究，运用弹性力学理论分析顶箔和波箔的变形，通过引入能量方程得到非等温Reynolds 方程，利用小扰动法处理非等温方程从而得到压力定常控制方程和压力微分控制方程，通过有限差分法和逐点松弛迭代法进行求解，实现了新型推力箔片轴承的气膜压力分布、气膜厚度分布、箔片变形分布、气膜温度分布、轴向刚度、轴向阻尼等特性参数的数值计算。

(3)在考虑箔片变形和气膜温度变化的条件下建立推力箔片轴承动态模型，数值研究了推力箔片轴承部分结构参数和运行参数对轴承轴向刚度和轴向阻尼的影响规律，绘制了相关曲线图。研究表明：箔片轴承的轴向刚度和轴向阻尼随着波拱半长、楔形间隙高度差、波拱半径的增加而减小。轴向刚度和轴向阻尼随着涡动频率比、转速、波箔厚度、顶箔厚度、轴承外径的增加而增加。可以看出转速、轴承外径对轴向刚度的影响比较明显，波箔厚度、顶箔厚度对轴向刚度的影响不太明显；楔形间隙高度差、波拱半径、轴承外径对轴向阻尼的影响明显，涡动频率比、转速对轴向阻尼的影响较小。