基于无量纲法两种一维溶质运移解的比较
2023-11-06付营帅
李 尧,付营帅
(西南交通大学土木工程学院, 四川成都 610000)
0 引言
改革开放以来我国经济发展取得了显著成就的同时也产生了许多严重的环境问题,尤其是土壤与地下水污染问题,已经严重危害到人类健康。土壤与地下水安全是人类赖以生存的保障和人类健康发展的前提。土壤及地下水是人类生产活动的重要物质基础。由于城市生活垃圾和工业“三废”的不合理处置,以及农药、化肥的大量使用,导致区域土壤、地下水污染状况日趋加重,对区域内居民饮水安全、粮食安全构成了严重威胁[1]。保护土壤和地下水资源是我国的重要任务,对我国的可持续发展战略起着至关重要的作用。随着环境污染问题日益严重,我国对环境污染的问题愈加重视,但目前缺乏对污染物在土壤和地下水中运移快速且有效的评估手段。
国内外许多学者研究污染物在土壤及地下水中运移数学模型,Ogata and Banks(1961)[2]基于土体为均质、各向同性且处于饱和状态,不考虑化学吸附作用和其他反应影响等假设建立了污染物在半无限厚度土层中的一维对流-弥散方程。van Genuchten (1981)[3]假设含水层为半无限含水层,基于拉普拉斯变换推导了在第一类边界条件(固定浓度边界)和第三类边界条件(可变通量边界条件)下无降解的溶质运移解析解。Bear(1972)and van Genuchten and Alves (1982)推导了包含降解在内的一维溶质运移解析解。Rowe and Booker(1985)[4]提出了在有限厚度的黏土层中包含对流、扩散-弥散、化学吸附作用的污染物一维运移半解析解并考虑了地下水流速对浓度分布的影响。Yeh等(2007)[5]基于拉普拉斯变换提出了在第一类和第三类边界条件下一维半无限介质中溶质运移方程解析解。王超等(1998)建立了水分和污染物之间耦合迁移理论模型,并通过有限差分法对污染物在非饱和分层土中迁移特性进行了研究。栾茂田等(2005)[6]对污染物顶部浓度采用了指数衰减关系,在有限厚度条件下进行了填埋场污染物运移过程数值模拟的一维计算。陈云敏等(2006)[7]和谢海建等(2008)[8]采用了分离变量法得出了成层土中污染物一维扩散解析解。
1 一维溶质运移解析解
溶质在多孔介质中运移主要受对流、分子扩散和机械弥散、吸附及分子降解等因素影响,其控制方程偏微分方程形式如式(1)所示。
(1)
式中:c为液相中溶质浓度;t为溶质运移时间;R为阻滞因子;Dij为水动力弥散系数,包括分子扩散系数与机械弥散系数;vi为实际水流速度;S表示包括生物降解和化学反应等一系列反应。
1.1 常浓度边界条件下溶质运移一维解
一维溶质运移控制方程见式(2)~式(5)。
(2)
常浓度边界条件:
C=C0,x=0
(3)

(4)
初始条件:
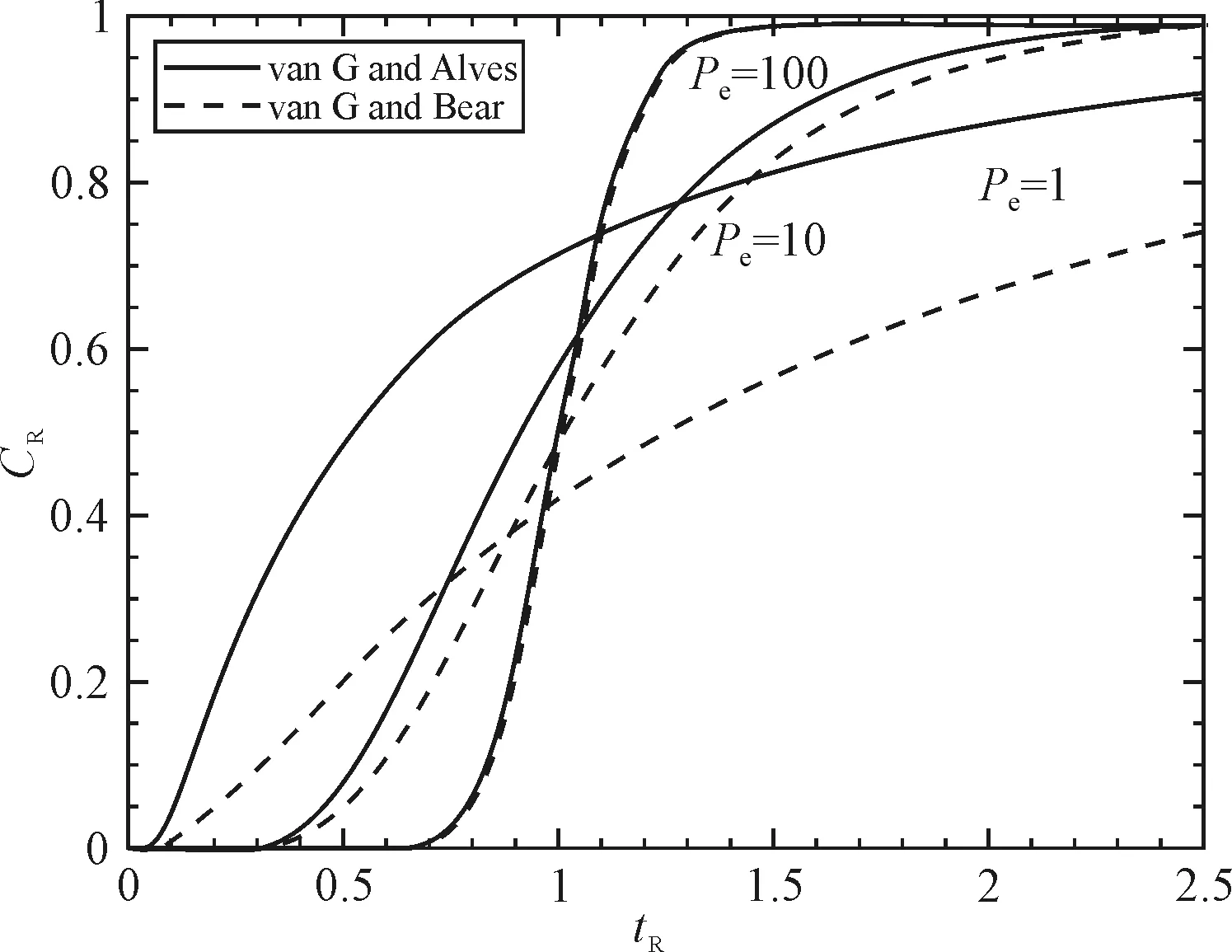
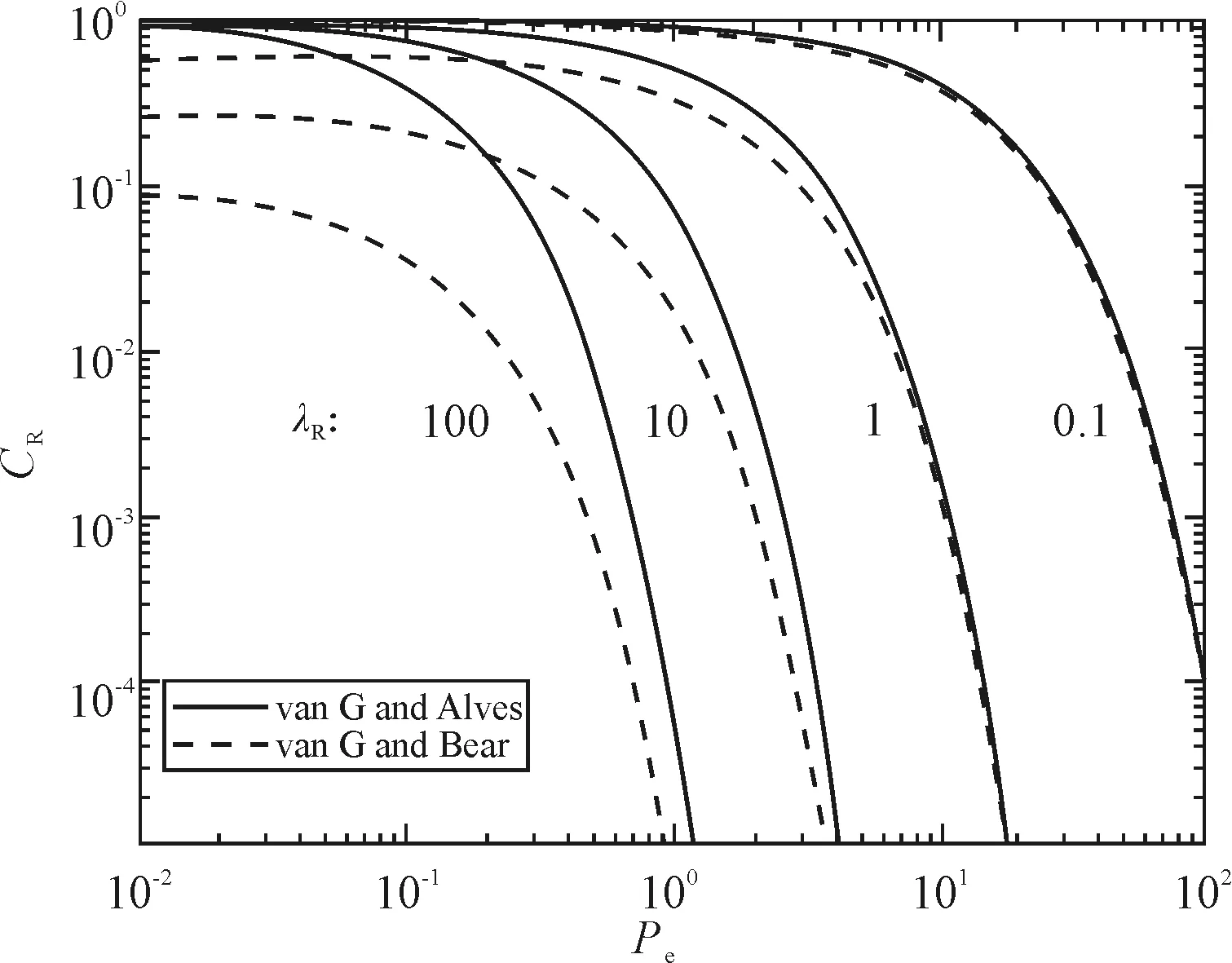
C=0,0 (5) 假设: (1)流体密度、粘度为常数。 (2)溶质具有一阶化学反应(对于保守溶质,λ=0)。 (3)流动只存在于x方向,并且速度为常数。 (4)纵向色散系数D为常数。 常浓度边界下解析解见式(6): (6) 一维溶质运移控制方程见式(7)~式(10)。 (7) 可变通量边界条件: (8) (9) 初始条件: C=0,0 (10) 假设: (1)流体密度、粘度为常数; (2)溶质具有一阶化学反应(对于保守溶质,λ=0); (3)流动只存在于x方向,并且速度为常数; (4)纵向色散系数D为常数。 可变通量边界条件下解析解见式(11)。 (11) 带有量纲方程在不同单位制下会多出不同的常数,通过数学变换对溶质运移方程中的变量进行无量纲分析变为真正描述溶质运移规律的量,使得方程明晰易懂。同时,无量纲参数比较适用于不同解析解间的比较,因为与使用实际参数相比,使用无量纲参数可以覆盖更广的参数值。 定义以下无量纲参数见式(12)。 (12) 式中:CR是相对浓度;tR是无量纲时间;Pe是贝克莱数;λR是无量纲一阶衰减常数;V是溶质运移速率;x是任意位置离污染源的距离;t是溶质运移时间;D是水动力弥散系数。 基于上述定义无量纲参数,式6变换为式(13)。 (13) 基于上述定义无量纲参数,式(11)变换为式(14)。 (14) 表1 无量纲参数取值 图1 一维溶质运移解无量纲曲线 图2 稳态条件下衰减对解的影响 图3 v G and Alves (1982)和v G and Bear (1972)不同无量纲时间值沿羽流中心线的解 使用某一典型污染场地参数说明上述2种溶质运移解析解的差异。污染源位于地下水位以下3 m,污染源浓度为358 mg/L,假设污染物位于的含水层是一维流动,其渗流速率为3.69×10-6m/s,污染物的有效弥散系数值为2.34×10-5m2/s,其一阶降解速率估计值为0.000 01 1/d。 图4根据贝克莱数定义给出从污染源到距离源头150 m处贝克莱数值,可以得到在距离污染源150 m内,贝克莱数在25以内变化。图5绘制了在0.3年、0.5年、1年时间范围内且降解速率为0.000 01 1/d时贝克莱数与CR曲线,可以看出v G and Alves (1982)和v G and Bear (1972)解的结果随着时间的增加相对浓度均逐渐降低,但两者的差异逐渐减小。图6绘制了0.3年、0.5年、1年时间范围内贝克莱数与相对浓度曲线图,此时一阶衰减速率为0.005 1/d,图6与图5比较可以看出,衰减越快其相对浓度降低越快。v G and Alves (1982)和v G and Bear (1972)解的结果相对浓度值差异不大,若初值浓度值较高,则相对浓度值微小的差异也会导致较大的结果。 图4 贝克莱数曲线 图5 v G and Alves (1982)和v G and Bear (1972)不同无量纲时间值下沿源中心线的解 图6 v G and Alves (1982)和v G and Bear (1972)不同无量纲时间值沿羽流中心线的解 用v G and Alves (1982)和v G and Bear (1972)提出的溶质运移一维解在无量纲时间和空间中计算恒定浓度下点源的衰减一维溶质运移可以更全面地考虑2种溶质运移解的差异。计算结果表明,沿着地下水流动方向,若以对流扩散为主导且污染物初始浓度较小,则2种解之间的差异在实际应用中可以忽略不计,但通常来讲由于v G and Alves (1982)解假设污染源为固定浓度,因此更加保守,但v G and Bear (1972)满足质量守恒定律可能更符合实际情况。如果对大量污染源进行快速浓度分布评估,应采取保守做法,优先选择v G and Alves (1982)的解。
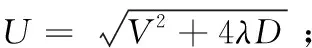
1.2 可变通量边界条件下污染物运移一维解


2 无量纲分析
2.1 第一类边界条件
2.2 第三类边界条件



3 案例计算



4 结果讨论
