基于VNABC 的多规格板材二维下料问题
2023-11-06徐震浩顾幸生
苏 俊, 徐震浩, 顾幸生
(华东理工大学能源化工过程智能制造教育部重点实验室, 上海 200237)
实现资源高效利用是绿色制造的重要课题,也是可持续发展的关键要素。制造业中的二维下料问题广泛存在于玻璃、木材、皮革、钢板等制造过程中。优化的下料方案能够有效地提高原料利用率,对降低生产成本、提高企业竞争力具有重要的意义。
二维下料问题(Two-Dimensional Cutting Stock Problem,2DCSP)在实际生产中的应用范围广,求解难度大,许多学者进行了大量研究。Clautiaux 等[1]研究了二维断头台切割库存问题中的单批次问题,提出一种基于列生成的潜水启发式方法,使用动态规划解决定价问题,同时利用部分枚举技术减少动态程序解空间中非正确模式的数量。Wang 等[2]针对允许刮削并考虑设置成本的2DCSP,建立了整数规划模型并使用了列和行生成算法,提出一种基于匹配级别的潜水启发式算法。Kwon 等[3]针对二维两阶段直线切割下料问题,提出了基于模式的模型并分析了全模式模型和阶段模式模型的列生成问题。上述研究的背景是单一板材且毛坯数量为单个,而实际生产中板材规格多样且毛坯较多。Supphakorn 等[4]考虑固定大小的可用余料,研究了具有多种库存的二维两阶段切割库存问题(2D-2CP),应用色谱柱生成技术试图找到一种使总浪费最小化的解决方案。Fabio 等[5]研究了具有不同可用库存且必须通过两阶段断头台切割的二维下料问题,提出并比较了3 种混合整数规划模型。Jin 等[6]针对库存多样且有缺陷的二维断头台切割问题,提出了一种新的基于树的两部分启发式算法。吴电建等[7]针对多规格、大批量的矩形件优化下料问题,提出了一种基于候选板条和连续启发式算法的面向可加工性的二维下料方法。杨威等[8]对大规模矩形零件在板材上的下料问题设计了基于剩余矩形匹配算法的遗传算法(LRFGA)。人工蜂群算法(Artificial Bee Colony Algorithm,ABC)是Dervis[9]于2005 年提出的一种智能算法,它具有结构简单、寻优能力强等优点,被广泛应用于各种工程领域,如电力系统、无人机轨迹规划、生产调度等。Bahriye 等[10]提出改进的MRABC 算法,引入了振动频率MR 以及变化的振动幅度SF,增强了算法的收敛能力。刘东林等[11]提出了基于花香浓度的人工蜂群算法(FABC),在传统的人工蜂群算法中加入了步长和视野范围这两个因素提升求解精度,并在侦查蜂阶段提出了花香浓度机制,避免陷入局部最优,提高收敛速度。
本文针对板材规格多样、毛坯规格多样且数量庞大的多规格板材二维下料问题,将下料过程分解成规整和非规整两个阶段,其中规整阶段提出组合块和零散块两种处理方法;并针对问题特点提出了一种变邻域人工蜂群算法(Variable Neighborhood Artificial Bee Colony Algorithm,VNABC)来求解优化模型。
1 模 型
多规格板材二维下料问题可以描述为:m种不同规格的板材,第i种规格板材用Pi表示,i∈I,I={1,2,···,m}。Pi的宽度为Wi,高度为Hi。k种不同规格的毛坯,第j种规格的毛坯用Rj表示,j∈J,J={1,2,···,k}。Rj的宽度为wj,高度为hj,需求量为cj。要求在不同规格的板材上下料给定数量的毛坯,下料时毛坯可以旋转90°,寻找合适的下料方案使所消耗的板材浪费率最低。
存在如下假设:不同规格的板材种类相同,数量不限;毛坯能在任意规格板材上下料;下料过程中毛坯从板材左下角开始下料,先向上叠加,再向右延伸;毛坯在板材上下料时只能90°旋转。
1.1 决策变量
决策变量如下:Ni:板材i的投入数量; λi,a,j,b:二进制变量,表示第a块Pi上第b块Rj的摆放,0 表示横放,1 表示竖放;X1i,a,j,b:第a块Pi上第b块Rj左下角的横坐标;Y1i,a,j,b:第a块Pi上第b块Rj左下角的纵坐标;X2i,a,j,b:第a块Pi上第b块Rj右上角的横坐标;Y2i,a,j,b:第a块Pi上第b块Rj右上角的纵坐标;ni,a,j:第a块Pi上Rj的数量; tls :板材的修剪损失。
1.2 约束
任意毛坯尺寸均小于所有板材尺寸。式(1)表示毛坯的高度不超过任意板材的高度,式(2)表示毛坯的宽度不超过任意板材的高度,式(3)和式(4)分别表示毛坯的高度、宽度不超过任意板材的宽度。
毛坯在板材上的位置与其摆放方式有关。式(5)和式(6)表明毛坯右上角坐标与毛坯左下角坐标的关系。
毛坯在板材上进行下料时,所有毛坯均应在板材的内部,不能超过板材的尺寸。式(7)和式(8)将毛坯的坐标约束在板材范围内。
式(9)表示该板材上所有毛坯面积之和不能大于该板材的面积。
式(10)表示在同一块板材上进行下料的任意两个毛坯不能重叠。假设有两个毛坯R1 和R2,R1 在R2 的左下方,它们的左下角坐标分别为 (X1,Y1) 和(X1′,Y1′),右上角坐标分别为 (X2,Y2) 和 (X2′,Y2′) ,则R1、R2 必须满足X2 ≤X1′或Y2 ≤Y1′才能保证两者不重叠。
式(11)表示每种毛坯的下料数量必须满足毛坯的需求量。
1.3 目标函数
以所消耗板材的浪费率为优化目标,如式(12)所示。
2 VNABC 算法
ABC 算法模拟蜜蜂采蜜行为,3 种蜜蜂以及作用分别为:引领蜂负责采蜜和传递信息,并将食物源的信息共享;跟随蜂获得食物源信息后选择一个较优的食物源采蜜;侦察蜂巡视所有食物源,一旦发现某个食物源枯竭,抛弃此食物源并寻找新的食物源。根据本文研究内容的特点,在ABC 算法的基础上提出了VNABC 算法,对模型进行求解。
2.1 编 码
针对多规格板材二维下料问题特点,将食物源设计成双层。第1 层表示毛坯下料顺序和摆放方式,正数表示横放,负数表示竖放,数字绝对值代表毛坯类型。第2 层表示板材,与第1 层数字对应。图1 所示的食物源中有5 种毛坯、2 种板材。毛坯的下料顺序是R4、R1、R3、R5、R2,其中R2 竖放,其余毛坯横放。其中R3 和R5 在P2 上下料,其余毛坯在P1 上下料。

图1 食物源Fig.1 Food source
2.2 解 码
食物源确定了每个毛坯对应的板材,根据该特点,设计两种不同的解码方案:(1)严格解码STD(Strict Decoding),毛坯只能下料到与之对应的板材上。例如图1 中R3 只能在P2 上下料,不能下料到P1;(2)松弛解码SLD(Slack Decoding),如果上一块板材剩余空间足够,则将当前毛坯下料到上一块板材上,否则在新的对应板材上下料。例如图1 中,如果上一块板材P1 能够下料R3,则R3 优先在P1 上下料,若P1 无法下料,则R3 在新的P2 上下料。
整个下料过程分为规整阶段和非规整阶段。规整阶段完成各规格毛坯主体下料任务,下料样式规整。非规整阶段下料剩余毛坯并且下料样式非规整。解码流程图如图2 所示。
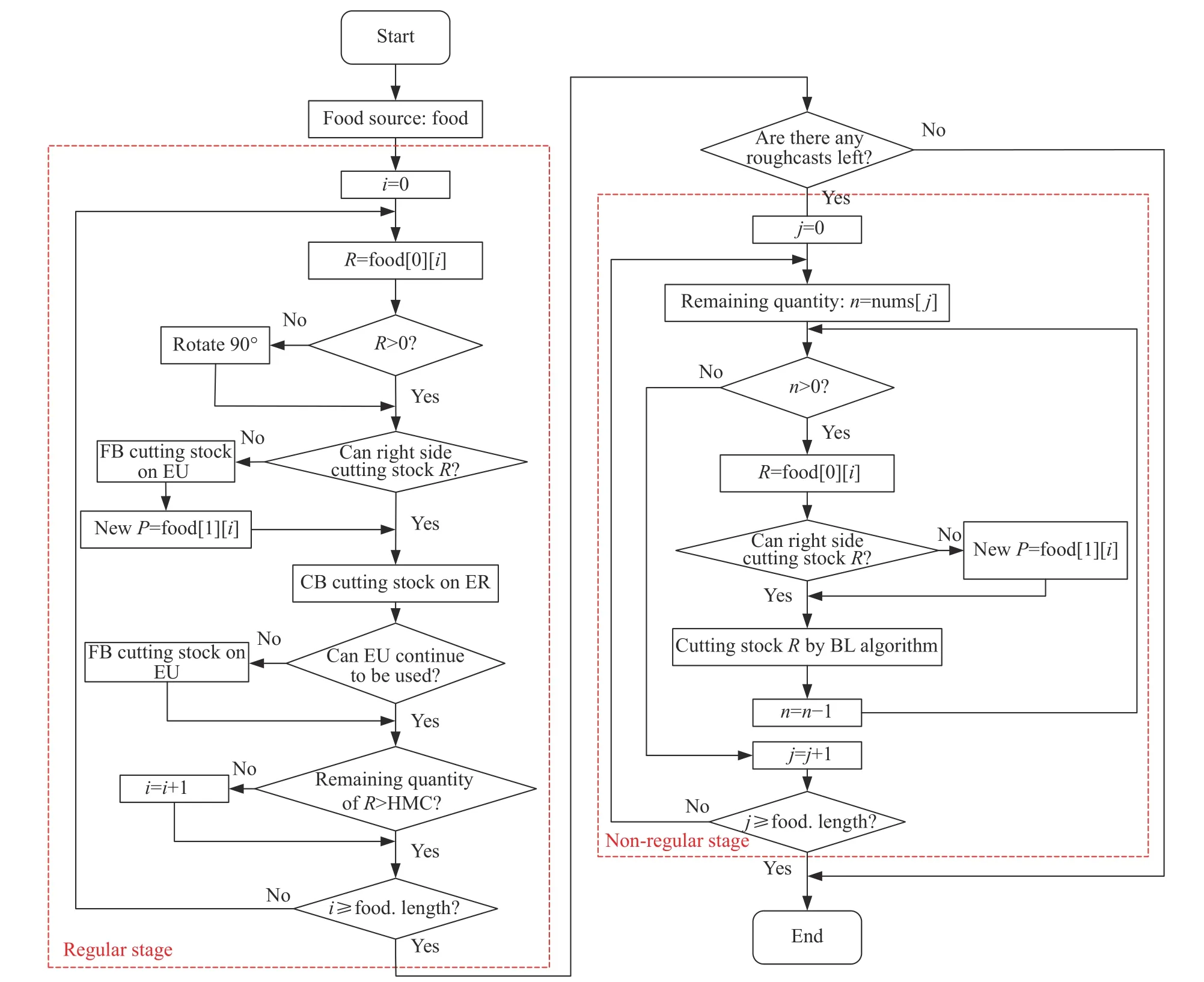
图2 解码流程图Fig.2 Flow chart of decode
2.2.1 规整阶段 规整阶段针对各规格毛坯设计了组合块CB(Combination Block)和零散块FB(Fragmentary Block)下料。对于某种毛坯,将板材高度方向上能够下料该毛坯的最大数量称为高度最大数量HMC。以HMC 个毛坯为一组向右连续下料,CB 就是由毛坯构成的矩形块。
FB 可以由不同规格的毛坯组成。在图3 中,当R3 所在的CB 下料结束,会产生上方余料EU(Empty Up),而R1 所在的CB 下料结束除了产生EU 外还会产生最右侧余料ER(Empty Right),零散块只能在EU 和ER 上下料。本文提出4 种零散块下料策略,一个台阶最优OS(One Step Optimum)下料、两个台阶最优TS(Two Step Optimum)下料、高度最优HO(Height Optimum)下料和宽度最优WO(Width Optimum)下料。以EU 为例,OS 下料策略为:首先针对EU 的最大高度,寻找可以放入的毛坯集合。在集合中寻找具有最大高度的毛坯,并从左向右依次填入EU 中,直到该高度的毛坯全部下料结束。如果右边剩余空间宽度小于阈值,则停止;否则在集合中寻找具有第2 高度的毛坯,在该层重复上述下料过程。直至该层填充结束,更新余料高度,如果余料高度超过阈值,则重复上述步骤,否则停止下料。OS 下料EU 或ER 的每一层只出现2 种高度,类似一个台阶。
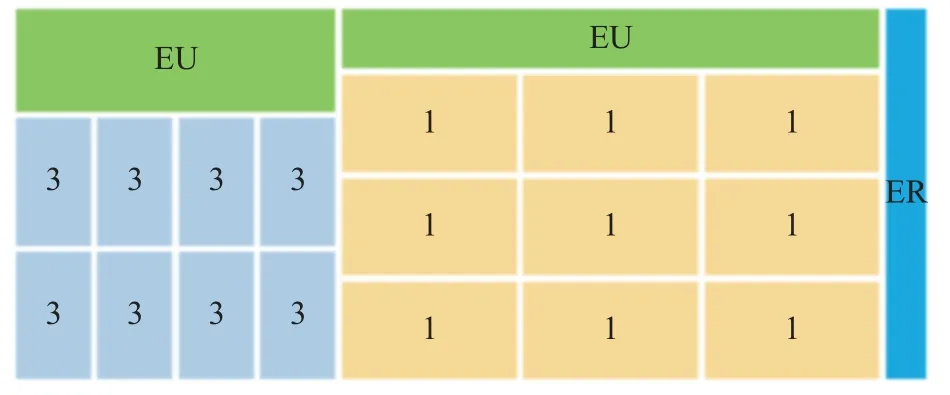
图3 毛坯下料Fig.3 Roughcast cutting stock
TS 下料过程和OS 类似,考虑到计算时间成本,TS 在OS 基础上对每一层余料多填充一次,因此每层最多出现3 种高度,类似两个台阶。对于HO 下料,首先找出毛坯的最优组合来填充余料的高。接着尽量填充每一层,允许不同规格的毛坯存在,但是要求毛坯高度一致。WO 下料和HO 下料类似,不同的是WO 下料寻找毛坯最优组合填充余料的宽,并尽量填充每一列。
2.2.2 非规整阶段 当规整阶段结束仍存在剩余毛坯时,则进入非规整阶段处理剩余毛坯,否则下料过程结束。由于规整阶段已经下料了大多数毛坯,剩余毛坯不多,故采用BL 算法(Bottom Left Algorithm)[12]解决非规整阶段下料问题。BL 算法的原理是毛坯每次从板材的右上角开始下料,不断向下、向左尝试移动,直到不能移动为止,期间该毛坯不能与其他毛坯重叠且不能越过板材的边界。
非规整阶段的下料需要考虑毛坯的下料顺序和摆放,也是复杂的组合优化问题。从剩余毛坯中找出较优的下料顺序和摆放时间成本太高,考虑到实际生产过程中的时间因素,非规整阶段毛坯的下料顺序和规整阶段保持一致,摆放方式为横放。
2.3 优化计算过程
针对双层食物源,为引领蜂和跟随蜂设计不同的邻域搜索策略。侦察蜂负责全局搜索,避免算法陷入局部最优,拓展算法搜索广度。
引领蜂邻域搜索采用变步长逆序交换方案。假设当前迭代次数是i,总的迭代次数为c,食物源的维度是d,则变化片段 fragment 的长度 len 为floor(d×(1-i/c))。随着i的增加, len 越来越小,有利于算法后期收敛。首先在区间 [0,d-1] 内产生一个随机位置a,从该位置开始往后寻找一个长度为 len 的区间,如果位置a到食物源末端的长度小于 len ,则往前寻找,直到区间的长度达到 len 。接着生成一个[0,1]之间的随机数r,如果r超过0.5,将变化区间所有的数字逆序,否则单点交换两个随机位置的数。最后,生成一个区间 [0,d-1] 内的随机位置,将该位置的元素乘以-1,表示毛坯旋转90°。
跟随蜂的邻域搜索采用比例加一方案。假设食物源维度为d,板材种类数量为m,则需要改变的元素个数 num=floor(d/5) ,如果 num <1 ,将 num 置为1。随机生成 num 个区间[0,d-1 ]内的位置,将食物源这些位置对应的元素加1,若加1 后的元素大于m,则置1。
侦察蜂的全局搜索采用重新初始化方案。具体为:假设食物源的长度为d,板材种类数量为m,食物源第1 层是乱序数字 1 ~d,并且随机给这些元素取负;食物源第2 层的每个元素都是从整数1~m中随机选取。
3 仿真实验与分析
3.1 参数设置
VNABC 算法中,主要参数包括食物源的数量N、迭代次数I和食物源探索上限L。采用响应面法来确定合适的参数,使用的工具为Design Expert 12。采用Box Behnken 实验设计,参数取值范围:N为40~100,I为500~1 000,L为50~100,得到拟合方程:Y=0.1812-0.0022×A-0.1115×B-0.0011×C,为了计算方便,参数均取整数值,N=100,I=1 000,L=75。表1 示出了模型的方差分析,P值小于0.050 0表示模型项显著,失拟F值为3.17,意味着失拟相对于纯误差并不显著,拟合效果好。实验结果表明模型建立合理,能够很好地预测试验结果。

表1 模型方差分析Table 1 Model variance analysis
3.2 测试数据
标准的二维下料问题的benchmark 数据里的板材规格都是单一的,且各规格毛坯数量也是单个。显然,不满足多规格板材二维下料问题的特征。由于多规格板材二维下料问题的复杂性,目前的研究成果不多,没有相应的标准测试数据,因此在二维下料问题benchmark 标准数据的基础上设计多规格板材二维下料问题的测试数据,选取了T 系、C 系和M 系。T 系出自Eva[13],有7 组实验,每组5 个,分别用a、b、c、d、e 表示。C 系出自Eva[14],7 组实验,每组3 个。T 系和C 系每种规格毛坯的数量在区间[20,100]内。M 系只有3 组实验,分别是 2×5 算例、3×10算例和 5× 19 算例。 2×5 算例[15]有2 种板材,5 种毛坯,板材规格为3 660 × 2 440 和3 300 × 2 134,毛坯信息为{900-360-5, 1 003-900-10, 600-550-18, 1 250-600-43, 856-475-25},其中格式x-y-z中x、y、z分别表示宽、高和需求量。 3×10 算例[16]有3 种板材,10 种毛坯, 板材规格为250×250, 300×250, 300×300。5×19算例[17]有5 种板材,19 种毛坯,板材规格为3 750×3 200、3 600×2 700、3 300×2 900、3 500×2 600 和3 800×3 000。
本文中的所有程序在Windows 10 系统、Intel Corei5 处理器、内存为16 GB 的PC 上使用Java 编写,JDK 版本为1.8。
3.3 性能比较
针对2.2 节提出的2 种解码策略和4 种零散块下料策略,组合出8 种不同的解码方案,分别是STDOS、 STD-TS、 STD-HO、 STD-WO、 SLD-OS、 SLDTS、SLD-HO、SLD-WO,分别简写为STO、STT、STH、STW、SLO、SLT、SLH 和SLW。对8 种解码方案进行测试,以浪费率 tls (百分比%)和计算时间t(ms)为评价指标,选取T1a、T2a、T3a 和T4a 这4 个测试数据,每个实验运行5 次。实验结果如表2 所示,其中 No.表示第几次实验,“~”表示该解码方案未能在1 min 内得到结果, tls 的最优结果加粗显示。
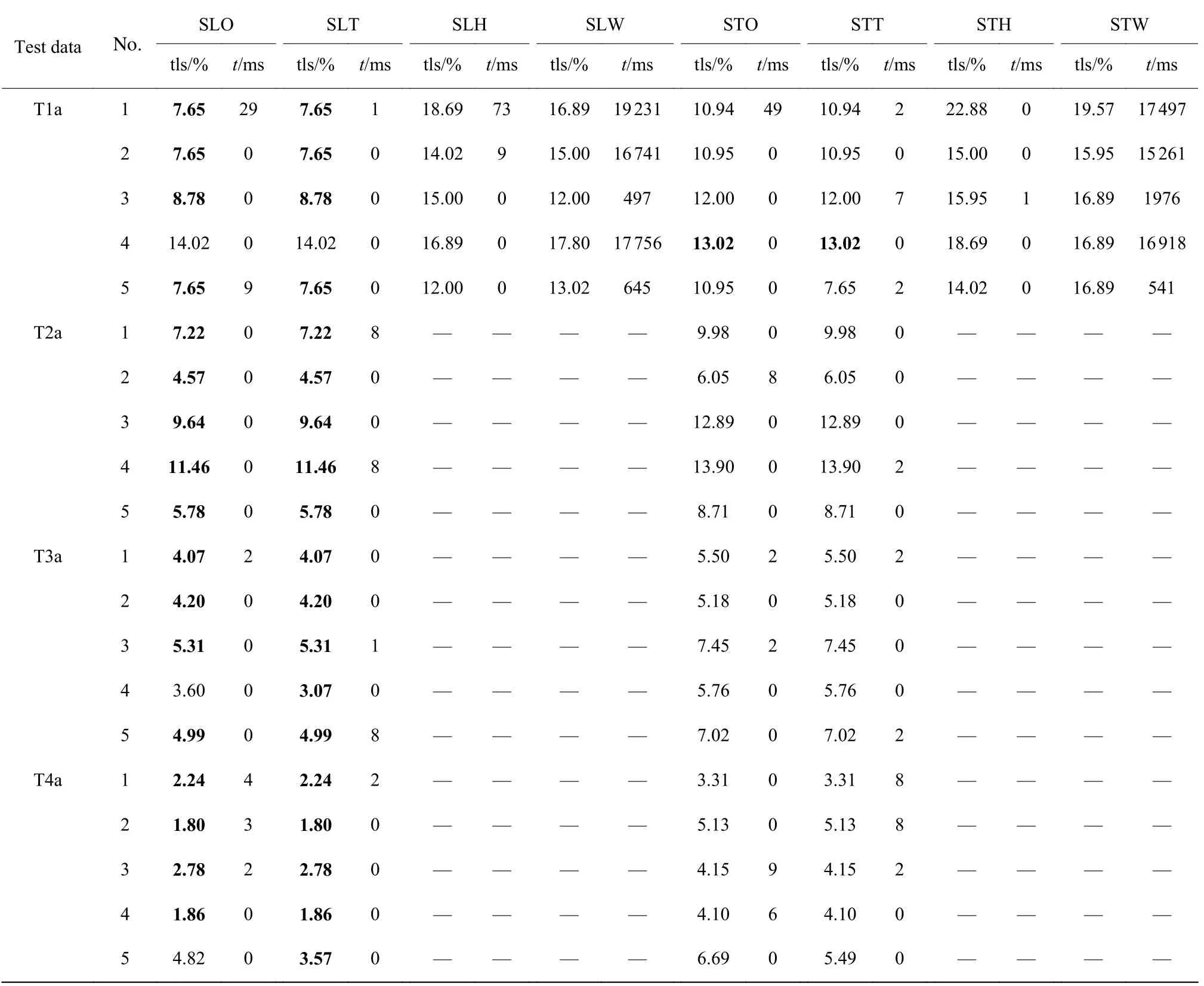
表2 解码方案对比Table 2 Decoding scheme comparison
从表2 中可以看出,对于浪费率 tls ,从解码策略的角度看,SLD 具有绝对的优势。除了T1a_4 中STO 和STT 的13.02 小于SLO 和SLT 的14.02 外,其余tls 都是SLO 和SLT 小于STO 和STT。从零散块下料策略的角度看,OS 和TS 也比HO 和WO 有优势,TS 比OS 更优。综上所述,解码方案采用SLT,即松弛解码和两个台阶下料。
下面以 2×5 算例为例介绍整个下料过程。毛坯中最小边为360,因此阈值设定为360。板材P1 规格为3 660×2 440,P2 规格为3 300×2 134。按照图1 所示食物源,R4 第1 个下料。8 块R4 组成的CB 下料到P1 上,上方余料EU 高度小于阈值,无法利用。接着由2 块R2 和1 块R1 组成的FB 下料到右侧余料ER 上,第1 块P1 下料结束,如图4(a)所示。在图4中,黑色数字表示毛坯,红色数字表示板材。R4 还有剩余,则继续在新的P1 下料,过程相同。等到第5 块P1 上R4 组成的CB 下料结束,R4 剩下1 块,小于R4 的HMC,轮到下一类毛坯下料。同理,R1 剩下1 块,小于R1 的HMC,轮到下一类毛坯下料。R3 理应在P2 上下料,由于松弛解码SLD 设定优先在上一块可下料板材上继续下料,因此R3 在上一块P1 上料,下料过程与之前类似。等到R2 下料结束,此时规整阶段结束,剩下1 片R4、1 片R1 和2 片R5,进入非规整阶段。非规整阶段使用BL 算法下料剩余毛坯的效果图如图4(h)所示。
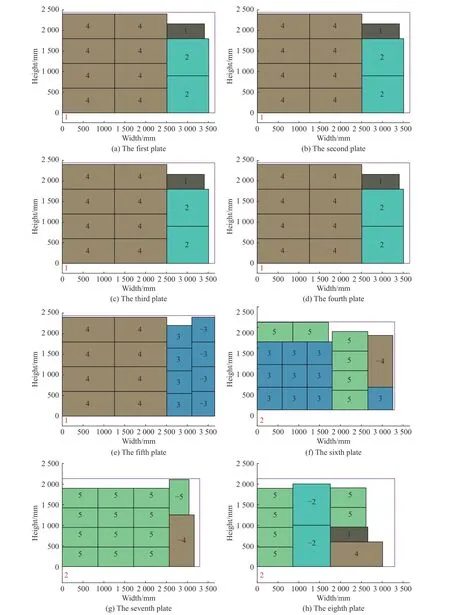
图4 2×5 算例下料方案Fig.4 2×5 cutting stock plan
为了验证VNABC 算法的性能,将其与遗传算法(GA)[18]、改进粒子群优化算法(NUS)[19]、模拟退火算法(SA)[20]和人工蜂群算法(ABC)[9]进行比较。所有算法采用相同的语言编写并且都在同一实验环境下运行,终止条件都设为1 000 次。VNABC 算法的参数为3.1 节响应面法确定的参数,而其余算法参数则按照文献里参数设置,每个实验运行10 次。算法性能指标由相对百分比偏差平均值(MRPD)、相对百分比偏差标准差(SDRPD)、相对百分比偏差最优值(BRPD)表示,它们的计算公式如下:
其中:ck表示算法第k次运算的结果,c*为所有算法得到的最优值。BRPD 指标越小,表明寻找到的解质量越高,越接近最优解。MRPD 指标越小,表明10 次运行的结果与最优值的偏差越小。而SDRPD 指标越小,表示10 次运行结果都较为接近MRPD,即算法的稳定性较好。
T 系的实验结果如表3 所示,其中T1~T7 括号中的数字表示毛坯的种类数量,各项性能指标最优值加粗显示。从表3 中可以看出,大多数实验中VNABC 算法的BRPD 指标为0,说明VNABC 算法找到的解是5 种算法中最优的,它的寻优能力较强。VNABC 算法的MRPD 指标和SDRPD 指标在T1~T4实验中几乎都是最小的,表明VNABC 算法在规模较小时稳定性较好且解的质量高。T5~T7 实验中,VNABC 算法的MRPD 指标和BRPD 指标也几乎都是最小的,但SDPRD 指标并非如此。例如T6a 中,VNABC 算法的MRPD 指标和BRPD 指标分别为0.28 和0,而SDRPD 指标为0.16,大于ABC 算法的SDRPD 指标0.10。这说明随着问题规模的变大,VNABC 算法稳定性变差。因此5 种算法中,VNABC算法的寻优能力较强,搜索空间大,这得益于两种蜜蜂不同的邻域搜索。
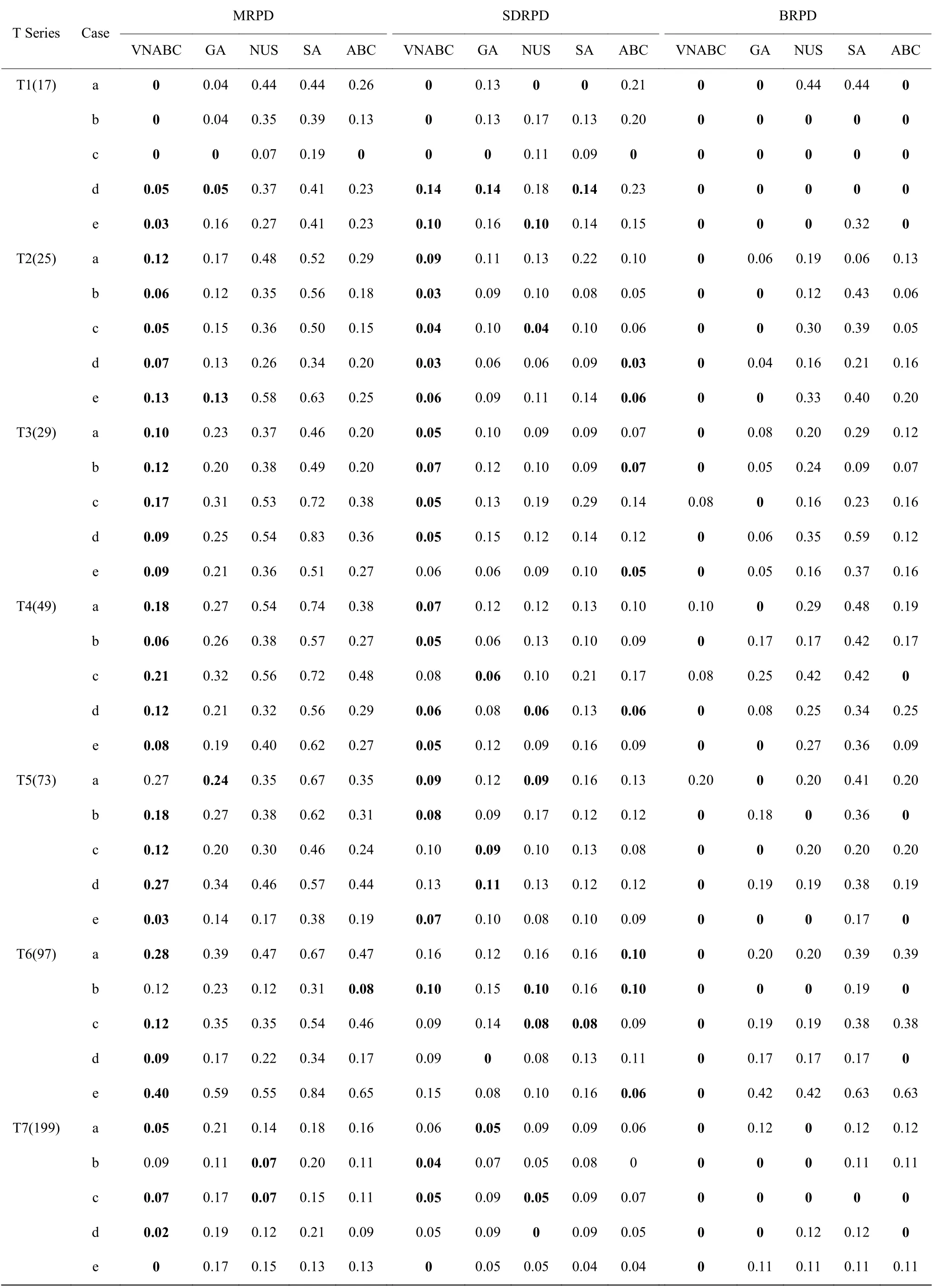
表3 T 系实验结果Table 3 Results of T series
C 系的实验结果如表4 所示。针对C1 和C2,5 种算法的3 个指标差距不大,效果都比较好。针对C3~C7,5 种算法的差距逐渐体现出来,其中SA 的结果最差。例如,C1-2 和C2-3 的5 种算法的指标都为0,表明5 种算法效果相同。C4-2、C5-3、C6-2 和C7-1 中VNABC 的3 种指标都取得了最低值,效果最佳。综合来看,VNABC 算法是最优的,其次是GA 算法。

表4 C 系实验结果Table 4 Results of C series
M 系中 2×5 算例、 3×10 算例和 5×19 算例的结果如表5 所示。3 个算例中,VNABC 算法除了3×10算例的SDRPD 指标0.37 不是最优外,其余指标都是最优,因此VNABC 算法具有明显优势。

表5 M 系实验结果Table 5 Results of M series
图5 示出了不同算例5 种算法的收敛曲线。从图5 中可以看出,VNABC 算法在计算过程前期收敛较快,得益于引领蜂的变步长逆序交换,搜索空间大;后期变化步长小,搜索空间变小,算法逐渐收敛。VNABC 算法能较好地解决该问题,寻优能力较强。

图5 不同算例部分收敛曲线Fig.5 Partial convergence curves of different examples
为了验证VNABC 算法具有普适性,增加单规格板材二维下料实验。矩形毛坯规格数据跟C 系保持一致,板材规格数据只取其中一种,实验结果如表6所示。表6 中出现了较多的0,这表明5 种算法取得了相同结果,出现这种情况的原因是板材规格和毛坯规格的差距过大,不管毛坯怎么摆放,它都能容纳毛坯,因此按照式(12)计算得到的利用率不会发生变化。C22 中,VNABC、NUS 和ABC 算法的BRPD为0,表明这些算法都找到了最优解。而VNABC 算法的MRPD 为15.37,优于其他算法,效果最好。同理,C32、C41、C42 和C51 中VNABC 算法均取得了最优结果。实验结果表明VNABC 算法可以用来解决其他同类问题。
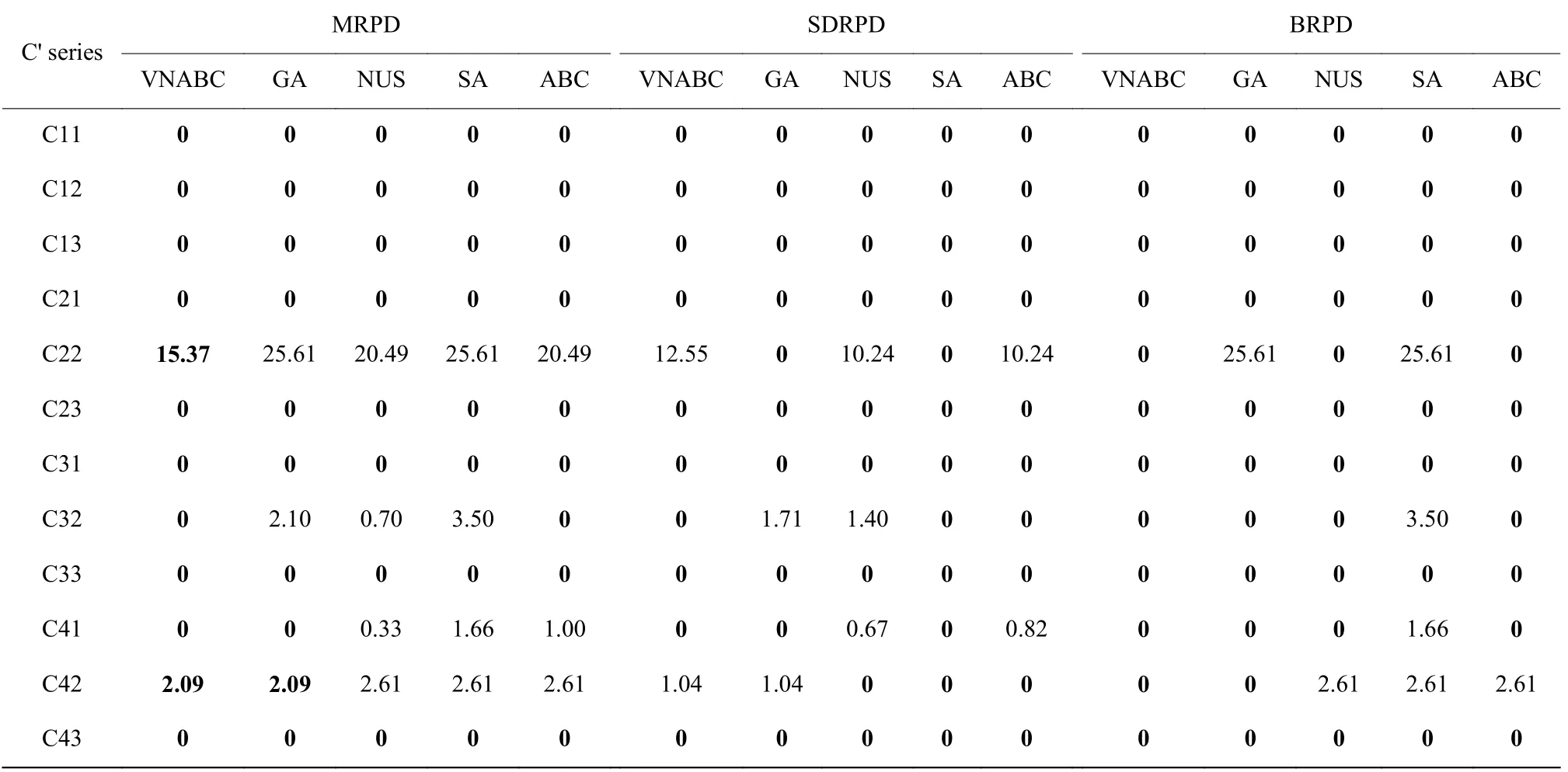
表6 单规格板材实验结果Table 6 Experimental results of single specification plate
4 结 论
本文在板材规格多样且数量不限的条件下,以板材浪费率最小为优化目标,研究了多规格板材二维下料问题:
(1)整个下料过程设计成两个阶段。规整阶段主要承担下料任务和下料规整,如果规整阶段结束仍有毛坯剩余,则非规整阶段使用BL 算法下料剩余毛坯。
(2)规整阶段设计了组合块和零散块下料过程。组合块在板材上下料,零散块在EU 和ER 两种余料上下料。针对零散块提出了4 种零散块下料策略,进一步降低板材浪费率。
(3)提出改进的VNABC 算法,设计双层编码并提出了两种不同的解码策略SLD 和STD。改进了VNABC 算法的3 种操作算子,提出变步长逆序交换的邻域搜索,提高算法性能。
(4)采用响应面法确定VNABC 算法的参数并且使用不同的数据集对VNABC 算法进行测试,将测试结果与GA、NUS、SA 和ABC 算法进行对比,实验结果验证了VNABC 算法解决多规格板材二维下料问题的可行性与高效性。同时,VNABC 算法能解决其他同类问题,具有一定的适应性。
