基于流固耦合的入水特性仿真与试验研究
2023-11-06付梦思秦绪国张雪娇
付梦思,薛 普,秦绪国,李 巍,张雪娇
(北京航天长征飞行器研究所,北京,100076)
0 引 言
跨介质飞行器是一种可在空中与水中巡航并能自由穿越水气界面的新概念海空两栖飞行器,它结合了潜艇和飞行器的优势,在军事和民用领域有着丰富应用。入水问题是一个非常复杂的涉及跨介质的固体及液体相互作用问题,在运动体入水过程中伴随许多现象,例如撞击、喷溅、入水空泡产生、空泡掐断、空泡溃灭等。
自1934年苏联工程师Ushakov提出飞行潜艇项目LPL 以来,研究人员针对不同的任务背景和作战要求,提出了多种跨介质飞行器。2005年,洛·马公司开展了潜射无人机鸬鹚的研制,并于2006 年11 月完成了溅落与回收验证试验。2011年,麻省理工学院的Amy Gao 等设计了一款仿生飞鱼跨介质飞行器。2014年,英国伦敦帝国理工学院Siddall等设计了一种跨介质飞行器AquaMAV,并于2017 年进行了喷射出水试验。2014年,巴西南里奥格兰德联邦大学的Paulo Drews-Jr等率先提出了将旋翼飞行器应用于跨介质任务,并设计了一种采用双层共轴八旋翼结构的多旋翼跨介质飞行器。2015年,美国奥克兰大学的Alzu'bi等设计了一种四旋翼跨介质无人机Loon Copter。2018年,约翰斯·霍普金斯大学Moore等设计了一种采用三角翼的跨介质飞行器,通过在水下建立足够的速度利用惯性实现水-空介质跨越,设计了最优出水轨迹并进行了有人操控的出水机动试验[1,7]。
跨介质飞行器提出至今,无论是在外形设计还是动力推进方面都有了很大的发展,但在空水介质转换方面缺乏研究,而空水介质转换时涉及飞行器、空气和水之间复杂的耦合作用,穿越水气界面、姿态瞬时变化时的载荷突变等,对飞行器的安全、稳定性至关重要,因此对跨介质飞行器进行入水特性的分析是十分必要的。
本文针对典型外形,采用任意拉格朗日-欧拉方法(Arbitrary Lagrangian-Eulerian Method,ALE)更好地解决复杂的流-固耦合问题和大变形问题。对不同入水速度的姿态、载荷等参数进行入水特性仿真分析,研究入水速度和入水角度对飞行器载荷和姿态的影响,并通过试验进一步验证仿真结果。
1 数值仿真模型
1.1 瞬态多相流控制方程
基于ALE 算法的质量守恒方程和动量守恒方程[2]为
式中x为空间坐标;ci为ALE描述下的对流速度,ci=vi-wi;vi为流体质点的物质速度;wi为网格速度;ρ为流体密度;bi为流体体积力;σij为应力张量。σij可表述为
式中p为水的静压;μd为动力黏性系数;δij为克罗内克常数。
1.2 流体状态方程
空气模型采用线性多项式状态方程[3],其压力计算公式为
式中c0~c6为材料常数;E为单位体积内能。
水采用Gruneisen 状态方程[4],其中μ为比体积,μ<0表示压缩,μ>0表示膨胀。
式中P为压力;S1,S2,S3为材料常数;γ0为Gruneisen系数;ρ0为水的密度。
1.3 刚体运动方程
本文计算的航行体以最大初始速度撞击水面的过程中不足以发生形变甚至折断,可不考虑飞行器结构的弹塑性变形,可视为刚体。
刚体运动方程[5]具体形式为
式中M为飞行器的质量;Ui为飞行器质心速度分量;Fi,Гi分别为流场对飞行器的力和力矩,通过对飞行器表面力进行积分求得;Jij为飞行器的转动惯量张量分量;Ωi为飞行器绕质心的转动角速度。
1.4 流固耦合计算方法
流体与结构之间的耦合作用通过流场ALE单元和结构拉格朗日单元材料之间的相互作用力来计算[6]。两种材料间的耦合力的算法是通过建立接触面上相互作用的主、从耦合点来计算,类似于罚函数接触算法,从搜寻到的主从耦合点之间建立线性弹簧关系计算耦合力,并且并联一阻尼器来消除高频振荡行为。
2 仿真计算
2.1 数值计算模型
计算模型外形长600 mm,直径80 mm,质量为3.8 kg,质心系数为0.55,如图1所示。

图1 计算模型Fig.1 Computational model
流体域网格中水和空气均采用六面体单元以提高计算精度和效率。其中飞行器采用拉格朗日网格,水和空气均采用欧拉网格,采用多物质ALE算法,定义飞行器与流体域之间的流固耦合关系,飞行器与水和空气之间采用罚函数算法,如图2所示。
2.2 数值验证
为了验证本文数值模型的计算精度,采用长40 mm、直径8 mm 的圆柱体结构入水试验模型进行验证,其以80 m/s的速度垂直入水,如图3所示。
在圆柱接触水面以后,速度迅速衰减,近似成指数衰减,随着运动速度降低,衰减趋势越来越缓。数值计算结果与试验结果比较接近,最大误差在10%以内,验证了本文所建立的数值模型具有良好的计算精度。
图4为球型首飞行器入水冲击载荷系数入水试验与数值仿真的对比结果。

图4 冲击载荷对比结果Fig.4 Comparison of acceleration
数值计算的结果与实验结果非常接近,再次验证了本文数值计算结果的精度和有效性。
3 试验验证
3.1 入水速度对载荷影响
采用如图1所示的实物模型进行入水试验,利用空气炮装置完成飞行器在炮管内的加速。选取40 m/s、60 m/s、80 m/s、100 m/s、120 m/s 的入水初速度来研究速度对入水载荷的影响。
图5为入水试验采集数据,飞行器在入水后短暂的时间内(1 ms 左右)轴向载荷由0 增加到第1 个峰值,之后逐渐振荡衰减趋于一个稳定值。在飞行器撞水以后,载荷虽然衰减,但是载荷曲线仍然会保持振荡的趋势衰减,且速度越大,振荡幅度越大。轴向载荷呈现出速度越大,峰值越大,峰值脉宽越窄的特点。
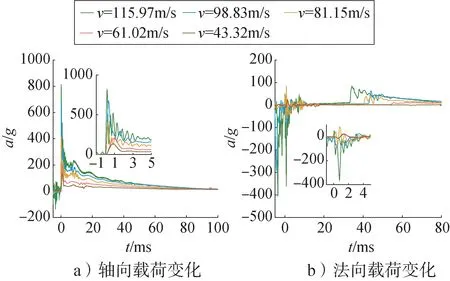
图5 载荷变化试验曲线Fig.5 Acceleration curve varying with time by test
入水速度98.83 m/s 条件下法向载荷变化略晚于81.15 m/s,是因为飞行器初速度越快,需要的高压气气压越大,飞行器出膛撞击水面开孔泡以后,炮管尾气继续对水面冲击。如图6所示,空泡尾端有大量的液面飞溅,根据伯努利原理,尾端形成低压区,不断卷入空气的同时还伴随着高压尾气的不断灌入,导致空泡直径和长度变大,飞行器尾拍的时刻要晚于81.15 m/s尾拍时刻,但是尾拍引起的法向载荷峰值要大于81.15 m/s条件下法向载荷峰值。
图7为入水速度100 m/s的载荷数值模拟与试验结果对比。

图7 载荷变化曲线对比Fig.7 Comparison of acceleration curve varying with time
在不同入水速度下,数值计算所得结论与试验保持一致。在相同入水速度下,ALE方法计算数值较试验值的均值稍高。飞行器在入水过程遭受的冲击载荷具有相似的变化规律:在触水瞬间,轴向、法向载荷急剧增加,在1 ms 之内达到峰值;之后迅速下降,最终趋于一个稳定的数值,即飞行器在入水过程中承受的最大载荷发生在入水冲击初期瞬态间(毫秒级)。
3.2 入水速度对姿态影响
飞行器头部触水后逐渐沾湿,由于介质突变,飞行器遭受巨大冲击载荷。在后续的入水过程中,飞行器头部所受的力主要由沾湿表面决定,如图8所示。

图8 入水姿态试验曲线Fig.8 Water-entry status curve by test
同一入水角度条件下,角速度整体呈先增大再减小的趋势。由于撞水速度越快,飞行器所承受法向载荷越大,俯仰力矩越大,初始入水速度越大,角速度在入水瞬间起始值越大。
对比峰值处左右两侧角速度变化趋势曲线可知,由于飞行器受水介质的阻力作用影响,其航行速度不断衰减导致飞行器的能量变低,且已经发生尾拍,飞行器背流面与空泡壁接触,受水阻力较大,法向载荷迅速增加,俯仰力矩变大,因此角加速度增大,角速度曲率变大。俯仰角的变化曲线的斜率呈现先增大再减小的趋势,与角速度变化趋势保持一致。
从图9中可以看出,在81.15 m/s条件下空泡尾端与炮管头部中间已经没有高压尾气,高压尾气已经散尽,不再灌入空泡内参与飞行器入水后的空泡演化过程。而98.83 m/s 条件下空泡尾端与炮管头部中间仍然具有很多尾气,在空泡尾端与液面飞溅共同形成气液混合态,在低压区的作用下与空气一起被卷入空泡,参与空泡的扩张和发展。因此飞行器在空泡中从航行到发生尾拍现象的俯仰运动时间增加,即发生这两个不同初速度条件下的尾拍时刻近似相同,主要原因在于98.83 m/s 发生尾拍现象的时间有所推迟。

图9 尾拍时刻空泡演化Fig.9 The evolution process of cavity at tail slapping
从图10 数值仿真与试验结果对比中得知,角速度和俯仰角的变化曲线的斜率呈现先增大再减小的趋势,试验结论与数值计算所得结论保持一致。
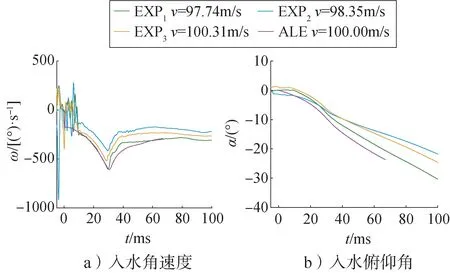
图10 入水姿态变化曲线Fig.10 Comparison of water-entry status curve
4 结 论
本文围绕飞行器入水冲击载荷特性及入水姿态变化,从数值计算与试验研究两个方面展开较为系统的研究,得出以下结论:
a)飞行器轴向和法向载荷峰值会随着速度的增大而增大,且脉冲宽度越窄;角速度峰值会随着速度增大而增大,且达到峰值的时间越短,角速度和俯仰角的变化曲线的斜率呈现先增大再减小的趋势。
b)轴向载荷是入水初期载荷的主导量,会随着速度、角度的增加呈线性增加;角速度峰值在不同速度、不同角度入水条件下规律相同,角速度峰值随着入水速度的增大而增大,增加量随着入水速度增大而增大。
