基于夜光遥感影像的苏南城市群建成区提取方法

朱凌一，王 勇

（1.南京信息工程大学长望学院，江苏 南京 210044；2.南京信息工程大学应用气象学院，江苏 南京 210044）

目前研究所使用的夜间灯光数据主要有DMSP-OLS 与NPP-VIIRS数据，后者拥有更高的空间分辨率和时间分辨率，且已经经过辐射定标。在对城市化的监测应用中，NPP-VIIRS数据也被证实其能力要优于DMSP-OLS 数据[1]。随着最新的NPP-VIIRS 夜光数据遥感影像发布，基于NPP-VIIRS数据提取城市建成区的方法体系还需完善[2]，目前急需基于NPP-VIIRS 数据提取城市群建成区的简单高效普适方法。因此，本文将基于2020年NPP-VIIRS夜光遥感数据，尝试构建基于差值平方函数的城市群建成区提取模型，并对苏南地区建成区进行特征分析，从面积、混淆矩阵和景观指数等方面将所建模型与阈值法进行对比分析，以期对苏南城市群国土空间规划制定、生态环境保护提供技术支持和决策参考。

1 研究区概况

本文选取苏南地区城市群（南京市、苏州市、镇江市、无锡市、常州市）作为研究区域，该地区位于长江三角洲中心区域，东邻上海，西接安徽，南靠浙江，北依长江；区内低山、丘陵、平原、江河、湖泊纵横交错，东部和中部较为低平，拥有广袤的太湖平原，水网密集，西部南京、镇江一带丘陵起伏；土地总面积2.79 万km2，占江苏省土地总面积27.17%，其中平原占苏南土地总面积50.45%，山地面积占28.4%，水域面积占21.15%。气候呈现四季分明、冬冷夏热，降水量在1 000 mm 以上，梅雨期内暴雨频发，强降水集中。苏南地区是中国经济最发达的区域之一，常住人口3 378.09 万人（2019年），城镇化率超过70%，所有县（市）都进入全国综合实力百强县行列，近年来苏南城市群建成区面积不断扩大。

2 数据来源与方法

2.1 数 据

本文采用美国国家大气和海洋管理局国家地理数据中心提供的2020年的NPP-VIIRS夜光遥感影像，空间分辨率约500 m，能够更精确、丰富地反映地表人类活动的空间信息。VIIRS 数据产品有“VCM”和“VCMSL”2种类型，为保证结果的准确性，本文选取“VCMSL”类型的VIIRS 影像，对其进行投影转换、重采样、裁剪等预处理，转换至分辨率为500 m 的阿尔伯斯等积圆锥投影坐标系，并裁剪苏南地区2020年月平均NPP-VIIRS 夜光遥感影像。此外，由于VIIRS数据产品并未去除陆地反射月光等背景噪声，本文还去除VIIRS影像的背景值。

为了验证建成区提取效果，同时考虑到Google Earth平台数据更新速度快，保证了数据的时效性，适合对成片的城市建成区进行目视解译[3]。本文采用Google Earth 软件所提 供的2020 年12 月Landsat8 卫星城市历史影像，在研究区内进行随机采样，同时对研究区随机采样点进行目视解译判断，并对本文所用方法的分类精度进行验证。

本文以GlobeLand30-2020土地利用类型数据为基准，从面积、混淆矩阵和景观指数等方面对比不同方法的建成区精度。GlobeLand30-2020数据是我国研制的30 m分辨率全球地表覆盖数据集，自然资源部对GlobeLand30数据集进行的最新更新，包含了更加丰富详尽的全球地表覆盖空间分布信息，能更好地刻画大多数人类土地利用活动及其所形成的景观格局，此数据是目前可免费获得的总体分类精度最高的地表覆盖数据。

2.2 数据预处理

由于NPP-VIIRS传感器较为敏感，城市建成区内部灯光辐射值增速较快[4]，在分析过程中会掩盖城郊过渡区的灯光变化较为平缓的特征。为了避免计算过程中像元DN值极端效应带来的影响，本文对原始NPP-VIIRS数据（图2a）进行筛选处理，结合先验知识与前人研究资料[5]，断定DN值大于20处为城市建成区（DN值≥20 的像元赋值为20），DN值小于1 处为非城市建成区（DN值≤1 的像元赋值为1），以此消除原始数据中的城市内部灯光突变和农村极小值噪声干扰，结果见图2b。为利用差值平方函数来进一步精确计算城市建成区与非建成区分界线提供数据基础。

2.3 方 法

2.3.1 差值平方函数

统计学中，方差是用来描述数据离散程度的数学函数，常常用来衡量数值之间的差异程度。本文基于方差的思路，使用相邻像元DN值之间的差值平方，来确定相邻像元DN值之间的差异，寻找这种差异变化的突变点，并将其作为城市建成区与非城市建成区的边界像元，从统计学意义上可以被视为是划分建成区与非建成区的标准，即定义为差值平方函数。差值平方函数公式为：

式中，DNi为第i个像元的灯光指数；Δ 为统计学意义上相邻2个像元的夜光指数的差值平方值。

2.3.2 验证方法

Google Earth影像空间比较法[6]在建成区提取精度分析方面具有操作简单和时效性强等优势。因此，本文选取Google Earth 平台于2020 年12 月成像的Landsat8 遥感影像作为研究区建成区和非建成区的验证数据，依据城市建成区在影像中的表现特征，通过目视解译的方式对建成区进行识别，同时ArcGIS软件在研究区内随机产生1 500个采样点，根据建成区和非建成区对采样点进行分类，随后与本文所用方法的分类结果进行对比分析，再进行精度评价。其中，分类精度的计算公式为：

式中，R为Google Earth与本文所用方法的提取结果相一致的点数；S为Google Earth 提取结果不一致的点数。通过对P值的分析，得出采样点分类的正确率。

2.3.3 混淆矩阵

在遥感影像处理中，混淆矩阵可以衡量遥感影像地物分类结果与地表真实地物结果之间的差异，这些差异可以用来描述遥感影像的分类精度。

本文使用建成区与非建成区分类结果作为实际划分建立建成区混淆矩阵，建成区混淆矩阵可以解读为：有x11个像元被正确分类为建成区，x22个像元被正确分类为非建成区；有x12个建成区像元被错分为非建成区像元，有x21个非建成区像元被错分为建成区像元。

基于以上结果，本文将进一步利用混淆矩阵，计算总体精度（OA）与Kappa 系数等分类精度指标。其中总体精度（OA）表示分类正确的像元点占总像元点的百分比，Kappa 系数常被视为衡量模型分类结果与实际分类结果是否一致的指标，值越大关系越好。具体公式如下：

式中，N为总样本点数，本文取值为1 500；r为总行数，本文取值为2；xii为主对角线上的值；xi+与x+j分别表示第i行和第j列的样本个数之和。本文将通过混淆矩阵计算总体精度与Kappa 系数，实现对提取建成区的精度评价。

2.3.4 景观指数

景观指标是分析地形空间模式的重要指标，也是验证城市区域制图精度的有效方法。由于混淆矩阵精度验证法无法展示提取的城市建成区与验证数据提取的城市建成区在空间和组织上的对比性，引入景观指标指数对比能够使精度验证更完善、全面、准确[7]。

常用的景观指数有景观形状指数（LSI）、周长面积比（PARA）和聚集指数（CONTIG）。其中LSI定义为景观格局中斑块的形状指数，通过计算区域内某斑块形状与相同面积的圆或正方形之间的偏离程度来测量形状的破碎程度，因此当建成区形态趋于破碎，LSI指数也随之提高；PARA是以斑块周长于面积的比值直接衡量形状复杂程度的简单指标，当PARA 指数增加时，城市建成区边界也更间断、离散；CONTIG指数反映地物中不同斑块类型的非随机性或聚集程度[8]，其值越大表明建成区越连续、聚集。本文将GlobeLand30-2020 中的人造地表数据作为验证样本，选取景观形状指数LSI、周长面积比PARA和聚集指数CONTIG等3个指数进行景观指数分析。

3 结果分析

3.1 城市群建成区提取模型构建

3.1.1 模型技术方案

为了寻找一种操作流程少，计算量不大且简单高效普适性强的城市群建成区提取方法，本文基于夜光遥感影像中的纹理特征，结合差值平方函数，挖掘夜光遥感影像的城市地物分布特征，实现建成区和非建成区的分类，本文将其定义为差值平方法。具体技术路线（图1）为构建基于差值平方函数的苏南城市群建成区提取模型。首先使用NPP-VIIRS夜光遥感影像数据，开展几何校正、去除噪声、提取研究区、筛选灯光亮度范围等预处理，结合差值平方函数逐行逐列计算，提取了建成区范围，然后与Google earth影像目视解译的采样点进行对比，实现空间精度验证。

本文所建的苏南城市群建成区提取模型的核心算法，就是采用差值平方函数检测边界像元。在遥感影像中，当像元间波动性达到一点程度，即2个像元DN值之间的差值平方达到局部极大值，可认为用来计算差值平方的2个像元分别属于两类不同的地物类型，而像元的交界处就是两类地物的边界。图1 给出经过差值平方计算后如何划分建成区与非建成区的示例，以一行为例，图1 的上部分为一行像元DN值，下部分为一行相邻两像元DN值的差值平方值。当DN值由较小值过度到较大值时，影像上具体表现为夜光遥感指数由低变高，即由非城市建成区过渡到城市建成区，而差值平方在DN值为10.877和16.433之间时达到最大值（30.87），故两点之间为城市建成区与非城市建成区的分界点，以此方法实现对夜光遥感影像的逐行逐列计算，提取研究区内的各个建成区边界点，再采用泰森多边形建立各个边界点DN值的代表范围，进而采用栅格计算器实现对建成区范围的提取，即将邻近分界点的夜光指数栅格DN值≥分界点DN值，此栅格定为城市建成区，否则定为非城市建成区。

3.1.2 精度验证结果

本文基于苏南地区2020年月平均NPP-VIIRS夜光遥感影像，采用上文所构建的建成区提取模型，提取了苏南城市群建成区范围。采用ArcGIS软件随机产生1 500 采样点和2020 年12 月Landsat8 遥感影像作为验证样本，根据目视解译对采样点进行建成区和非建成区分类，再采用混淆矩阵与差值平方法分类结果进行对比，总体精度为93.6%，表明基于差值平方法提取的建成区与苏南地区实际建成区分布结果具有高度的一致性。

3.2 苏南城市群建成区特征分析

根据基于差值平方函数的NPP-VIIRS夜光遥感影像建成区提取模型，实现了苏南城市群建成区的提取，结果如图2所示。图2a为差值平方函数所得边界点，已经凸显了城市建成区与非城市建成区之间的过渡带，可以大致反映出城市内部的建成区空间分布特征。

在所求得边界点的基础上，通过ArcGIS软件中泰森多边形实现各个边界点DN值的代表范围，进而采用栅格计算器实现苏南城市群建成区的提取，最终分类结果如图2b所示。苏南城市群中城市建成区总体呈现苏锡常趋于一体、南京独占一角的分布态势，从数据上来看，南京、镇江、常州、无锡、苏州的城市像元所占比例分别为22.64%、19.45%、19.94%、28.36%与26.84%；按建成区面积指标排序为苏州（2 144.63 km2）>南京（1 703.12 km2）>无锡（1 305.53 km2）>常州（869.39 km2）>镇江（747.80 km2）。差异的产生与各个城市不同的自然、社会经济条件及不同的城市规划方案等有着密切的关系。与实际的建成区相对比发现，提取结果与实际建成区像元占比、建成区实际位置、城市实际土地利用类型较为一致，表明差值平方法在能对城市实际建成区的比例与城市空间范围起到很好的解释作用。

3.3 与阈值法对比

目前，阈值法是在城市建成区提取中最常见的方法，其利用二分法计算影像分类阈值。当在某一阈值下的城市建成区面积最接近于统计数据的数值时即可认为此阈值为分割阈值[7,10]，通过确定分割阈值进行分类，实现城市建成区范围的划分与确定。为进一步验证差值平方法是否有效提高了城市建成区的提取精度，本文以GlobeLand30-2020土地利用类型数据为基准，对差值平方法与阈值法提取的建成区范围进行比较，并从面积、混淆矩阵和景观指数等方面定量分析了建成区提取精度。

1）面积精度分析。本文统计了研究区内各市的建成区面积，结果见表1。以GlobeLand30-2020 中的人造地表数据的面积作为验证数据，采用差值平方法的城市建成区面积准确率平均值为97.71%，而高于采用率阈值法的92.44%，表明在夜间灯光影像，差值平方法提取的建成区精度更高，提取面积更接近真实城市建成区。差值平方法不仅可以保证城市建成区的整体形态，还可以剔除城市建成区中的非城市建成区影响，效果较为理想。

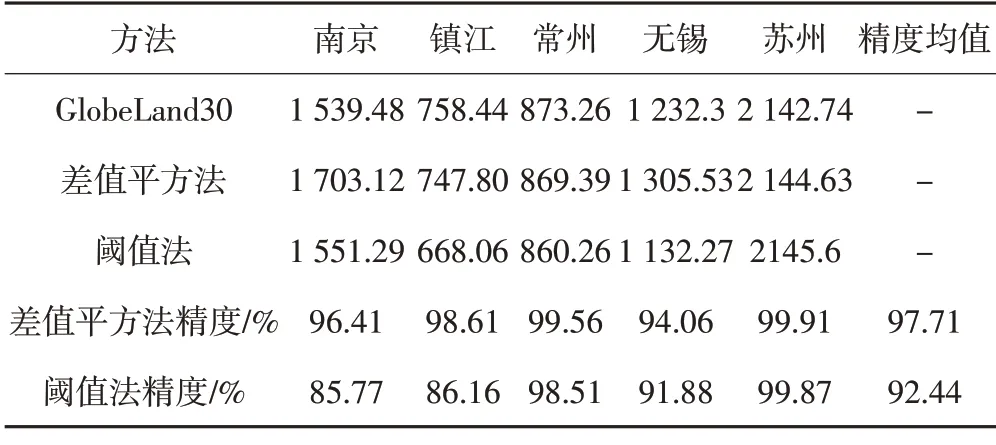
表1 基于差值平方法和阈值法的城市建成区面积精度评价/km2

2）混淆矩阵精度评价。在定量评价指标方面，面积误差和混淆矩阵常用于衡量图像提取和分类精度。采用混淆矩阵进行精度评价，计算出总体精度和Kappa 系数2个指标，2 种方法的对比结果见表2。差值平方法与阈值法的平均总体精度为84.36%与84.40%，2 种方法差别很小，而它们的Kappa 系数分别为56.23%与55.38%，这表明总体上差值平方法提取效果优于阈值法。

表2 基于差值平方法和阈值法的城市建成区混淆矩阵精度评价/%

3）景观指数精度评价。根据差值平方法和阈值法的建成区提取结果，采用Fragstats 软件进行景观指数分析。考虑到GlobeLand30-2020数据空间分辨率较高（30 m）导致不同用地类型边缘破碎的情况，本文将其进行重采样为500 m×500 m 的空间分辨率，使其与差值平方法和阈值法的提取结果栅格一致，再进行景观指数分析（表3）。从表3中的结果来看，差值平方法和阈值法的LSI 指数相近，与GlobeLand30-2020相距较大；差值平方法与GlobeLand30-2020土地利用类型数据的PARA 指数接近，而CONTIG指数完全一致，总体优于阈值法，因此差值平方法提取的城市内部建成区与GlobeLand30-2020土地利用类型数据中人造地表数据呈现更高的景观一致性，更接近实际情况。

表3 基于差值平方法和阈值法的城市建成区景观指数精度评价

4 结论

本文利用苏南地区2020年月平均NPP-VIIRS夜光遥感影像，建立了基于差值平方函数的城市群建成区提取模型，实现了苏南地区城市群建成区范围的提取，结合GlobeLand30-2020土地利用分类数据，与阈值法进行对比分析，具体结论如下：

1）本文对NPP-VIIRS 夜光遥感影像数据开展几何校正、去除噪声、提取研究区、筛选灯光亮度范围等预处理，构建了基于差值平方函数的建成区提取模型。并采用ArcGIS 随机产生1 500个采样点和Landsat8 遥感影像作为验证样本，得出差值平方法提取的建成区与苏南地区实际建成区分布结果具有高度的一致性。

2）基于差值平方法和NPP-VIIRS 夜光遥感影像所构的建成区提取模型，实现了苏南城市群建成区的提取。南京、镇江、常州、无锡、苏州的建成区像元比例分别为22.64%、19.45%、19.94%、28.36%与26.84%，按建成区面积指标排序为苏州>南京>无锡>常州>镇江。与实际的建成区相对比发现，采用差值平方法能对城市实际建成区的占比与城市空间范围起到很好的解释作用。

3）从面积、混淆矩阵和景观指数等方面对差值平方法与阈值法提取的建成区进行精度分析，差值平方法提取的城市建成区面积准确率高于率阈值法，差值平方法与阈值法的平均总体精度相近，而差值平方法的Kappa 系数高于阈值法，差值平方法的景观指数更接近实际情况，进一步证明差值平方法能够有效提高城市建成区的提取精度。