ECDSA协同签名方案设计与实现

彭金辉 雷宗华 张志鸿

1(郑州信大捷安移动信息安全关键技术国家地方联合工程实验室 郑州 450004)

2(郑州大学计算机与人工智能学院 郑州 450001)

(pjh@xdja.com)

椭圆曲线数字签名算法(elliptic curve digital signature algorithm,ECDSA)[1]和RSA/DSA相比,具有处理速度快、带宽和存储占用小的特点[2],广泛应用于电子商务、移动安全接入等领域,可提供身份认证、密钥协商、签名验证等服务.在密码应用安全技术体系[3]中,签名方案的安全性依赖于私钥存储环境和运算环境的安全[4],私钥安全通常由安全芯片、智能密码钥匙、PCI-E密码卡、服务器密码机等硬件密码模块提供保障.随着公钥密码算法的普及,特别是在工业互联网[5]、物联网[6]、车联网[7]、加密货币[8]、区块链[9]等领域的广泛应用,智能终端设备可通过安装加密TF卡、加密NM卡和加密SIM卡等外设,或者通过在主板硬贴片TPM/TCM/TPCM等模块,实现配置硬件密码模块,但更多的智能终端设备不具备上述条件.针对这种场景的软件密码模块应运而生,并得到快速发展.对于软件密码模块,其私钥需要在终端设备上存储和运行,可采用口令派生密钥、本地多份存储或者其他方式加密保护,但由于互联网中这些智能终端设备大多属于个人用户,缺乏有效的私钥保护环境,敏感信息非常容易被敌手攻击甚至窃取,造成经济损失.基于安全多方计算[10]和门限签名[11]的思想,一个可行的方案是将私钥分拆成2个或多个分量,各分量独立产生、存储和运算,私钥签名操作通过多方协同运算完成,不重构完整私钥也可得到合法的签名结果.

针对ECDSA双方协同运算,一些方案被提出：Lindell等人[12-13]提出了基于Paillier同态加密算法的两方协同ECDSA签名方案,但是计算开销和存储开销比较大,签名运算效率受限;Doerner等人[14-15]提出了基于秘密共享和不经意传输技术的(2,n)门限签名方案,无需引入计算开销较高的同态加密及相关零知识证明,提高了协同签名的计算性能,但不经意传输协议增加了大量的通信带宽开销;王婧等人[16]通过预计算一次一密的Beaver三元组,利用其安全两方乘法技术,避免计算量大的同态运算和通信开销大的不经意传输等操作,实现相对高效的两方协同签名,但该方案需要大量的预计算;严莹子[17]提出了基于多方(t,n)门限的拆分方案,但该方案使用了加法同态加密、不经意传输、承诺机制、零知识证明、秘密共享等,运算量和传输量均较大.

除ECDSA之外,针对商用密码算法：龙毅宏[18]和冯琦等人[19]通过数学公式巧妙构造安全高效的SM2双方协同签名的方案;尚铭等人[20]基于秘密乘积的分享、秘密逆的分享、点乘的分享等设计了SM2门限签名方案;Mu等人[21]设计了基于Paillier的两方协同SM9算法签名方案.

针对现有ECDSA双方协同签名方案的不足,本文设计了一个协同签名方案C-ECDSA(collaborative ECDSA),通过数学公式构造了双方协同产生密钥对、协同签名的过程,在恶意模型下增加零知识证明.避免了使用计算开销大的同态运算和通信量开销大的不经意传输;避免了使用一次一密的各种预计算、预存储;避免了秘密的分享;在通信双方其中一方可能被攻击腐化的情况下,能够有效保护签名私钥安全.

本文首先介绍标准ECDSA签名算法,然后给出C-ECDSA方案设计,包括协同产生密钥对运算过程、协同签名运算过程,并给出签名结果的正确性证明.通过零知识证明和模拟协议给出了方案的安全性分析,最后给出了在智能终端上的验证以及性能分析.

1 ECDSA签名算法

本节概要介绍ECDSA算法产生密钥对和私钥签名算法的标准流程[22].

1.1 符号定义

定义椭圆曲线E的参数为params=(p,a,b,G,n),其中a,b为椭圆曲线方程的参数,p为大素数,椭圆曲线上坐标x,y的运算均模p,G为椭圆曲线基点(Gx,Gy),n为椭圆曲线上G的阶,[k]P表示椭圆曲线上P的k倍点.

1.2 产生密钥对

1) 使用随机数发生器产生整数d∈[1,n-2];

2) 计算椭圆曲线点P=(x,y)=[d]G;

3) 输出密钥对(d,P),其中d为私钥,P为公钥.

1.3 签名算法

1) 对待签名消息M使用预定的杂凑算法(如SHA256),得到消息摘要e;

2) 产生随机数k∈[1,n-1],根据k生成椭圆曲线点(x1,y1)=[k]G;

3) 计算签名结果第1部分r=x1modn,如果r=0,返回步骤2);

4) 计算签名结果第2部分s=k-1(e+rd) modn,如果s=0,返回步骤2);

5) (r,s)为最终签名结果.

2 安全模型

2.1 安全模型和设计目标

本节描述安全性证明所依赖的安全模型,通过构造模拟协议,利用和被攻击方的交互,将安全性规约到ECDSA原始签名方案的安全假设.

安全模型参照了文献[19]的方法：

首先是通信模型,假设2个通信方共享ECDSA系统参数和曲线参数,且存在一个点对点通道用于双方协议通信.

其次是敌手能力,假设概率多项式时间(P.P.T)敌手E是恶意的,它可以在协议执行过程中任意地偏离协议过程.如果通信双方都被E控制,分析没有意义.有以下4条假设：假设E可以控制其中一方,且知道被控制方的所有秘密值;假设在协议执行之前就确定E攻击哪一方,在协议执行过程中不发生角色改变;在安全证明过程中,假设通信的每一轮都由诚实方首先发给被控制方;假设E的视图包括被攻击方所有的输入、随机数和协议需要传输的所有数据.

第三是安全目标,传统的私钥签名方案安全性证明模型是选择明文攻击下的存在性不可伪造的安全模型EU-CMA(existential unforgeability against chosen-message attack).该模型假定敌手E已知公钥且可以选择任何消息进行签名验证.

在EU-CMA模型中,假定签名方案为π,如果敌手E在多项式次签名验证后,仍无法以一个不可忽略的概率伪造一个新消息的签名,那么签名方案π是可证明安全的,即

Pr[Expπ,E(1λ)=1]≤ε,

(1)

其中Expπ,E(1λ)是对ECDSA原始签名方案的伪造,ε为一个可忽略概率阈值,λ是安全参数.

协同签名方案本质是一种分布式签名生成方案,签名值在传统验证算法下是有效的,本文把协同签名方案的存在性不可伪造称为C-EU-CMA(collaborative EU-CMA).

在C-EU-CMA模型中,假定签名方案为Π,如果P.P.T敌手E控制了2个通信方的其中一方μ(μ取值为通信方A或者通信方B),同时允许E取得协同签名的协议实例,E仍然无法以一个不可忽略的概率伪造出一个新消息的签名,那么该协同签名协议满足存在性不可伪造的安全性,即

(2)

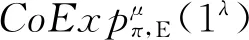
2.2 安全两方计算

安全两方计算最早由姚期智提出,要求通信双方不泄露各自敏感数据的情况下,执行各自计算逻辑并最终获得计算结果,双方除了各自输入数据、有关中间计算数据以外无法获得任何额外有效信息[10].针对ECDSA双方协同产生密钥对和协同签名运算,可描述为：通信双方分别产生各自子私钥d1和d2,协同产生公钥P,根据待签名消息摘要e和随机数R(包括各自随机数R1,R2),执行签名运算过程S(R,e,d1,d2)得到可被公钥P验证通过的签名值(r,s).

要求协同签名满足以下条件：1)私密性,协同运算执行过程中双方传递的数据不会泄露各自子私钥的相关信息;2)正确性,签名结果使用对应公钥能够验证;3)安全性,和原始签名算法具有相同的安全性.

安全多方计算根据参与方诚实度分为半诚实模型和恶意模型.半诚实模型能够正确地遵循协议的指令,但会记录执行期间的中间数据,并企图得到额外信息,只要通信双方不泄露自己的输入,该模型就是安全的;恶意模型指敌手可能任意违背协议的指令,一般包括诚实方、恶意方和可信方.

2.3 零知识证明理想函数

在通用可组合安全框架下,理想函数是重要的组成部分,代表一个不可被攻击的可信方,用来完成协议所需的理想功能与执行过程.敌手E与任一通信方的交互用于模拟协议的现实执行过程.任一通信方(包括可视为理想敌手的模拟器)与理想函数的交互用于模拟协议的理想执行过程[16].

根据Lindell等人[13]的定义,标准零知识证明理想函数可以形式化表示为

Fzk：((x,w),λ)→(λ,(x,R(x,w))),

其中λ为公共参数,R定义了声明x和证据w的关系.在本文方案中,R特指关于循环群上椭圆曲线离散对数关系的零知识证明：Q=[k]P,即点Q关于点P的离散对数为k.Fzk函数收到通信方A的消息,且R验证有效,向通信方B发送证明;收到通信方B的消息,且R验证有效,向通信方A发送证明.

3 方案设计

本文方案中涉及2个参与方：通信方A和通信方B,方案内容包括协同产生密钥对和协同签名2部分.

3.1 协同产生密钥对设计

C-ECDSA方案协同产生密钥对设计流程共包含8步,具体如下：

1) 通信方A执行以下3步.

A1.通过随机数模块产生随机数d1∈[1,n-1],作为A的子私钥持久存储;

A2.根据d1和G计算得到椭圆曲线点P1=[d1]G;

A3.向理想函数Fzk发送P1关于G的离散对数是d1的零知识证明,并将客户端身份标识IDA和P1通过网络模块发送给B(如果通信异常或者数据丢失,重新从A1开始执行).

2) 通信方B在收到P1后,执行以下4步.

B1.判断理想函数Fzk返回的零知识证明有效性,若无效则终止协议;否则通过随机数模块产生随机数d2,d3∈[1,n-1],作为B端IDA对应的子私钥持久存储;

B3.计算P=P2-P3,P作为公钥持久存储;

3) 通信方A在收到P2和P3后,执行以下步骤：

A4.判断理想函数Fzk返回的P2零知识证明有效性,若无效则终止协议;否则计算P=P2-P3,P作为公钥持久存储.

至此,协同产生密钥对完成,双方拥有了各自的子私钥和公钥.

上述完整步骤流程如图1所示：

图1 C-ECDSA方案协同产生密钥对流程

公钥P的计算公式在数学上展开：

令

(3)

则P=[d]G,此时d相当于完整私钥.

3.2 协同签名设计

C-ECDSA方案协同签名设计流程共包含11步,具体实现如下：

1) 通信方A执行以下3步.

A1.对待签名消息M使用预定的杂凑函数,得到消息摘要e;

A2.通过随机数模块产生随机数k1∈[1,n-1],根据k1和G生成第1部分签名Q=[k1]G;

A3.向理想函数Fzk发送Q关于G的离散对数是k1的零知识证明,并将客户端身份标识IDA和e,Q通过网络模块发送给B(如果通信异常或者数据丢失,将重新从A1开始执行).

2) 通信方B在收到IDA,e,Q后,通过IDA查找该客户端对应私钥d2和d3,并执行以下6步.

B1.判断理想函数Fzk返回的Q零知识证明有效性,若无效则终止协议;否则通过随机数模块产生随机数k2,k3∈[1,n-1];

B3.根据x1和e计算得到第2部分签名r=x1modn,若r=0,返回步骤B1;

B4.根据k2,k3,d2,e,r计算得到第3部分签名s1=k3(k2+d3) (e+rd2) modn;

B6.将第2,3,4部分签名r,s1,s2通过网络模块发送给A,如果通信异常或者数据丢失,将重新从A1开始执行.

3) 通信方A在收到r,s1,s2后,执行以下2步.

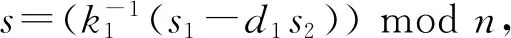
A5.将(r,s)作为最终签名结果.

上述完整步骤流程如图2所示：

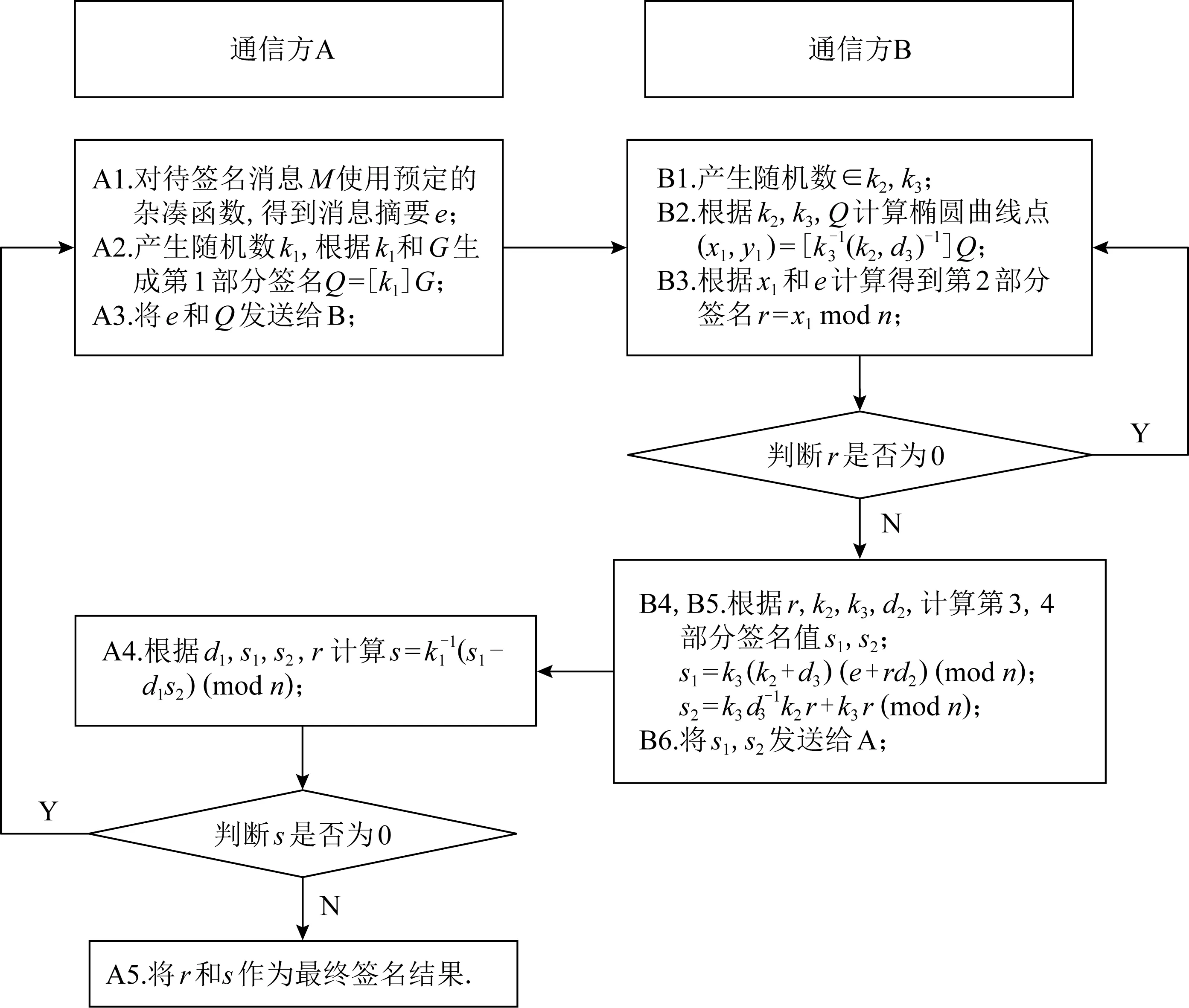
图2 C-ECDSA方案协同签名流程

把通信方B第2步计算的椭圆曲线点的公式在数学上展开：

令

(4)

则(x1,y1)=[k]G.

式(4)中k相当于基于完整私钥d作ECDSA原始签名运算步骤2)的随机数.

此外,当实际场景安全要求较低时,方案可删除基于理想函数的零知识证明相关协议,构成半诚实模型下的协同签名方案,提高运算效率.

3.3 协同签名正确性证明

要利用C-ECDSA方案进行签名,必须要证明其协同签名与标准ECDSA签名算法是等价的.

定理1.C-ECDSA方案协同签名结果和ECDSA原始签名结果等价.

证明.根据ECDSA签名算法可知,要证明C-ECDSA方案协同签名结果和完整私钥签名结果是等价的,只需要证明s=k-1(e+rd).

根据式(4),令

根据式(3),有

证毕.

4 安全性分析

C-ECDSA方案协同产生密钥对和协同签名算法的安全性基于原始ECDSA产生密钥对和签名算法安全性.

定理2.C-ECDSA协同运算过程中双方传递的通信数据不泄露双方私有敏感数据.

在密钥对产生过程中,公开数据P1,P2,P3是安全的,基于椭圆曲线离散对数难题,无法通过P1,P2,P3推算出任何和私钥d及其分量d1,d2,d3的有关数据.

签名过程中,客户端计算Q,服务端计算r,s1,s2,从Q,r,s1,s2无法得到任何与私钥d及其分量d1,d2,d3以及随机数k的有关信息.

综上,协同运算过程双方传递通信的数据不会泄露双方任何私有敏感数据.

定理3.假设原始ECDSA签名方案是不可伪造的,在随机谕示器和零知识证明模型下,本文提出的两方ECDSA协同签名协议满足存在性不可伪造.

证明.本文方案的安全性证明遵从模拟规约的证明方法,假设概率多项式时间敌手E以不可忽略的概率ε在C-ECDSA协同签名方案中伪造成功,那么将构造一个模拟器在原始ECDSA签名方案中充当伪造者,且伪造成功的概率也是不可忽略的.由于本文方案包括通信方A和通信方B这2个角色,下面分别考虑A和B被攻击2种情况,并分别说明模拟密钥生成和模拟协同签名协议.

4.1 通信方A被攻击

假设通信方A被敌手E攻击(腐化),下面构造一个模拟协议,其中S是模拟器,其任务是提取被腐化的通信方A的输入,生成一个敌手不可区分的执行视图,并利用敌手构造的伪造签名攻击原始ECDSA签名方案.

1) 模拟生成密钥对.

A1.模拟器S询问ECDSA密钥生成谕示器FECDSA,得到一个公钥P;

A2.模拟器S向通信方A(即敌手E)发起协同产生密钥对指示;

A3.当接收到敌手E发来的P1,以及发给理想函数Fzk的P1关于G的离散对数为d1的证明,模拟器S验证P1=[d1]G是否成立,若不成立则终止协议;否则执行下一步;

A4.模拟器S产生随机点P2,并计算P3=P2-P,把P2和P3发给敌手E;

A5.模拟器S模拟Fzk向敌手E发送关于P2和P3的零知识证明有效;

A6.模拟器S存储P,P2,P3,d1,若敌手E诚实计算,必定会通过计算P2-P3得到正确的P.

2) 模拟协同签名.

A1.模拟器S执行签名谕示器FECDSA,得到一个关于消息摘要e的签名结果(r,s);

A2.模拟器S向敌手E发起协同签名请求;

A3.模拟器S接收到敌手E发来的Q,以及发给Fzk的Q关于G的离散对数为k1的证明;

A4.模拟器S验证Q=[k1]G是否成立,若不成立则终止协议,否则继续;

A5.模拟器S从签名中恢复出R=(x1,y1)=[s-1]([e]G+[r]P),从而得到r=x1modn;

A6.模拟器S随机选择k3和k2并计算s2=k3k2r+k3r,s1=k1s+d1s2,将r,s1,s2发送给敌手E;

A7.模拟器S模拟Fzk向敌手E发送关于R的零知识证明有效;

A8.若敌手E诚实计算,必定会输出正确的ECDSA签名(r,s).

3) 不可区分性分析.

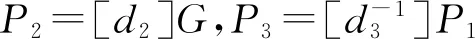
类似地,协同签名的现实执行环境和模拟执行环境的区别是R的计算方法和s1,s2的计算方法.协议现实执行环境R由随机数k2,k3和点Q计算得到,模拟执行环境中R由签名信息r,s和公钥P中恢复出R=[s-1]([e]G+[r]P),由于r,s和公钥P是FECDSA随机选取的,所以2个R分布相同,均满足均匀随机分布.现实执行环境中,s1,s2根据k2,k3,d2,e,r计算得到,分布是随机的;模拟执行环境中,s1,s2根据k1,k2,k3,d1,s,r计算得到,分布也是随机的,二者均满足随机分布,敌手视角不可区分.此外,如果敌手E偏离协议,模拟器可以通过验证Q和s来判断,如果验证失败则终止协议,这与现实执行环境一致.最后模拟器输出有效签名(r,s),即从FECDSA得到的签名.综上所述,对于敌手E来说,模拟执行环境和现实执行环境是不可区分的.

4) 签名伪造.

由于敌手E攻击通信方A后,无法区分模拟执行环境和现实执行环境,故模拟器可以调用敌手E的伪造签名攻击原始ECDSA签名方案.

4.2 通信方B被攻击

假设通信方B被敌手E攻击(被腐化),下面是构造一个模拟协议：

1) 模拟生成密钥对.

A1.模拟器S询问ECDSA密钥生成谕示器FECDSA,得到一个公钥P;

A2.模拟器S产生一个随机点P1发送给敌手E;

A3.模拟器S模拟Fzk向敌手E发送关于P1的零知识证明有效;

2) 模拟协同签名.

A1.模拟器S询问签名谕示器FECDSA,得到一个关于消息摘要e的签名结果(r,s);

A2.模拟器S从签名中恢复R=[s-1]([e]G+[r]P),模拟器S通过获取敌手E的随机数k2,k3和私钥分量d3计算Q=[k3(k2+d3)]R,并将Q发送给敌手E;

A3.模拟器S模拟Fzk向敌手E发送关于Q的零知识证明有效;

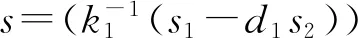
3) 不可区分性分析.

类似通信方A被攻击的情况,本文简要分析通信方B被攻击时敌手视图不可区分.

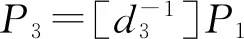
4) 签名伪造.

由于敌手E攻击通信方B后,无法区分模拟执行环境和现实执行环境,故模拟器S可以调用敌手E的伪造签名攻击原始ECDSA签名方案.

在模拟协议执行过程中,敌手E生成的签名验证公钥P通过谕示器FECDSA获得,故E在模拟协议中对协同签名的伪造也可以作为对标准ECDSA的伪造.可见,若敌手E以不可忽略的概率ε赢得协同签名方案,那么模拟器S可以同样的概率ε赢得原始签名方案.由于原始ECDSA是可证明安全的,即模拟器S伪造签名成功的概率是可忽略的,敌手E伪造成功的概率也是可忽略的,因此假设ε不可忽略是不成立的,说明本文方案在通信方B被攻击时是安全的.

证毕.

5 方案实现和性能评估

5.1 软件架构设计

下面给出本文方案的一个具体实现场景的软件设计.通信方A是智能终端上运行的软件密码模块,软件形态为运行在嵌入式Linux,Android系统上的客户端APP;通信方B是协同签名服务器,带有PCI-E密码卡,软件形态是运行在Linux操作系统上的服务端Server.

协同签名算法通过C语言实现.软件架构主要包括密码服务接口模块、大整数运算模块、椭圆曲线运算模块、ECDSA协同运算模块、随机数模块、网络通信模块等,如图3所示：

图3 软件模块结构

最顶层是密码服务接口模块,向APP提供协同产生密钥对、协同签名接口.该模块依赖ECDSA协同签名模块、数据存储模块和网络通信模块.服务端Server不单独提供密码服务,作为软件密码模块的配套使用.

ECDSA协同运算模块基于椭圆曲线运算模块和随机数模块封装了协同产生密钥对接口和协同签名运算接口.

随机数模块可产生指定比特长度的随机数.

椭圆曲线运算模块基于大整数运算模块封装了点加、倍点、点乘等运算.

大整数运算模块提供大数的模加(c=(a+b) modn)、模减(c=(a-b) modn)、模乘(c=(a×b) modn)、模逆(c=a-1modn)等运算.

网络通信模块用于建立客户端和服务端之间的连接.

客户端存储模块用于存储自身的子私钥等敏感数据信息(d1和P),客户端支持存储多个协同密钥对.

服务端存储模块用于存储客户端身份标识、服务端子私钥等敏感信息(d2,d3,P),服务端可存储多个客户端的协同密钥对.

5.2 性能分析

下面通过统计协同运算过程中使用的主要运算量和网络传输数据量对本文方案和对照方案进行分析,对照方案分别为Lindell[12]方案、Doerner等人[14]方案、王婧等人[16]方案.

采用符号KP表示椭圆曲线倍点运算,KG表示椭圆曲线G点的倍点运算,HH表示摘要运算的耗时,用PP表示一次同态运算耗时(包括加密、解密、乘),NL表示Paillier公钥长度.与上述运算比较,少量的点加、大数加、大数乘和哈希运算的耗时可忽略不计.用λ表示椭圆曲线运算中域上元素长度.

测试用的椭圆曲线参数(p,a,b,G,n)选择NIST推荐的secp256r1,哈希算法选择SHA-256,λ取值为256b.测试用客户端身份标识均按256b计算.

下面分析半诚实模型下的各方案的理论运算和通信开销.Lindell[12]方案中,NL=8λ=2048;Doerner等人[14]方案中摘要计算的个数是在安全参数256的情况下统计的.本文方案中主要运算开销是通信方A的1次固定点乘运算和通信方B的1次非固定点乘运算,总耗时为2KP.传输开销主要是IDA,e,Q和r,s1,s2,点Q长度l(Q)=l(Qx,Qy)=2λ,通信有效数据长度L=l(IDA)+l(e)+l(Q)+l(r)+l(s1)+l(s2)=32×8+λ+2λ+λ+λ+λ=256+6λ=1792b.半诚实模型下各方案2个通信方的理论运算开销如表1所示,理论通信开销如表2所示.

表1 半诚实模型下理论运算开销比较

表2 半诚实模型下理论通信开销比较 b

恶意模型下,Lindell[12]方案增加执行椭圆曲线离散对数的零知识证明协议;Doerner等人[14]方案增加执行一致性检测协议;王婧等人[16]方案和本文方案增加执行椭圆曲线离散对数的零知识证明协议.各方案的理论计算开销如表3所示,理论通信开销如表4所示.

表3 恶意模型下理论运算开销比较

表4 恶意模型下理论通信开销比较 b

在仿真测试中,测试主机CPU为Intel i7-7700 3.6GHz,对照组参考了王婧等人[16]方案提供的测试方法和数据,如表5所示：

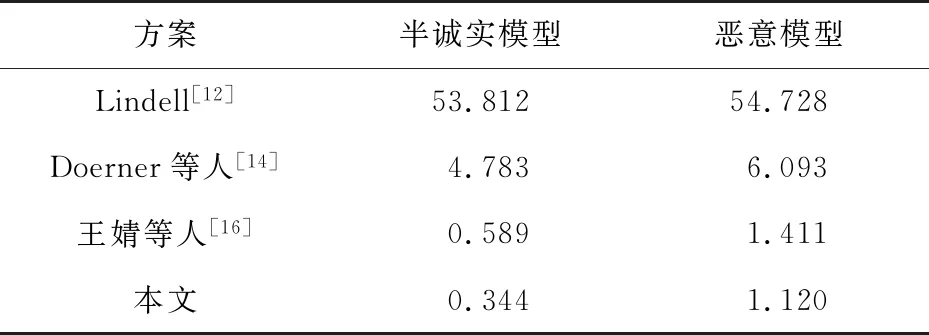
表5 仿真运算开销比较 ms

6 方案延伸

本节给出由本协同签名方案延伸的几种私钥拆分方法,差异部分如表6所示,其中A表示通信方A产生的敏感数据(其中di表示私钥分量,ki表示随机数,i表示整数),B表示通信方B产生的敏感数据.公式“d=”表示完整私钥表达式,公式“k=”表示签名随机数k的表达式,表达式“si”表示通信方B计算的签名中间数据.

表6 本文方案延伸的几种私钥拆分方法

7 结 语

在互联网场景下,协同签名方案是解决智能终端软件密码模块私钥安全的关键.现有两方和多方ECDSA协同签名方案存在运算效率偏低、通信开销过大等问题,影响在智能终端用户推广.本文提出的C-ECDSA协同签名方案,通过密钥分存分算的算法设计充分保证协同运算的安全性,实现对智能终端软件密码模块签名私钥的隐私保护,并较大提高协同签名运算效率.本文给出了方案的安全性分析及接近的几种私钥拆分方法.在性能开销上,理论分析和实测数据表明,本文方案具有运算效率高、通信开销低的优点.

在实际应用中,通信方A作为移动智能终端的软件密码模块,通信方B作为协同签名服务器,本文方案可广泛应用于移动金融、移动政务、智能电表、V2X车联网等互联网领域.