基于随机森林特征选择的BiLSTM电解槽出铝量预测
2023-11-03孙少聪徐杨曹斌
孙少聪,徐杨,曹斌
(1.贵州大学 大数据与信息工程学院,贵州 贵阳 550025;2.中铝智能科技发展有限公司,浙江 杭州 311100)
在新型工业化道路战略的带动下,“坚持以信息化带动工业化,以工业化促进信息化”的指导思想,大型铝电解厂生产管理由人力、手动为主的模式向自动化和智能化模式的转变已势在必行[1]。铝电解生产是一个大延迟、多变量耦合和非线性的过程[2]。其中关于电解槽出铝量预测问题就受到各种复杂的因素影响,如设备环境,工艺参数,人工经验等。因此如何从现有采集的大量数据利用机器学习和深度学习等技术,建立准确的预测模型提高预测的准确性和科学性,对企业的“降本增效”具有重要意义。
目前已有部分结合机器学习和深度学习的方法对出铝量预测进行研究,减少专家知识和经验对电解槽出铝量的影响,其中文献[3]提出了一种基于电解槽出铝量预测的聚类算法,实现了电解槽出铝量的参数特征提取;文献[4]将循环卷积神经网络LSTM算法,运用在电解槽出铝量预测和氟化铝添加量的预测问题上,并且开发了一套铝电解槽出铝量预测可视化系统;文献[5]设计了一种自适应果蝇优化算法,通过机器学习支持向量回归机对电解槽出铝量进行预测;文献[6]将多层感知机MLP应用在出铝量的预测;文献[7]文中提出一种改进的ID3算法,应用回归分析计算各条件属性影响出铝量的权重,对铝电解数据库中包含的出铝量专家知识和经验进行知识表示和自动推理,辅助工艺管理人员做出科学判断,提高生产智能管理水平。上述研究对电解槽出铝量预测方面都提供了一定的参考价值,但是目前对于电解槽出铝量预测问题依然很难应用于实际生产。
综上,本文提出了一种基于随机森林特征选择的双向长短期时间序列网络(RF-BiLSTM)进行电解槽出铝量预测,通过特征选择、优化模型参数,以及多个对比实验表明RF-BiLSTM在电解槽出铝量预测准确度方面取得不错的效果,并在实际的生产数据中验证了模型有效性,为铝电解槽出铝量预测提供一定的参考价值。
1 相关理论
1.1 皮尔逊相关系数原理
皮尔逊相关系数法是一种准确度量两个变量之间的关系密切程度的统计学的方法[8]。皮尔逊相关系数的变化范围为-1到1。系数的值为1或者-1意味着主指标和特征值可以很好的由直线方程来描述,所有的数据点都很好的落在一条直线上,1表示特征值随着主指标的增加而增加,-1表示特征值随着主指标的增加而减少。系数的绝对值值越接近0意味着二者之间线性关系越弱,为0则表示二者没有线性关系,Pearson计算原理公式如下:
(1)
式中:r表示相关系数,X表示主指标,Y为特征值。
1.2 随机森林相关性分析原理
随机森林(random forests, RF)是由多棵决策树集成的有监督的学习算法,在决策树的训练过程中随机选择特征,最终通过投票来表决最优结果[9]。随机森林算法简单,因为其简单高效的分类性能,在特征选择问题中往往是较好的选择。随机森林利用袋外数据(out of bag, OOB)误差计算特征变量相对重要性,对海量高维数据进行剔除冗余特征进行特征筛选。假设有bootstrap样本k=2,3…,K,K表示训练样本的个数,每个样本有N维特征,特征重要性排序的计算步骤如下:
1) 初始化k=1,创建决策树Tk。
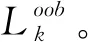
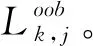
4) 对于k=2,3…,K重复步骤1~步骤3。
5) 特征Xj的重要性度量Pj通过公式(2)计算。
6)对Pj降序排列,得到特征重要性排序。

(2)
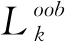
1.3 BiLSTM模型原理
LSTM是一种特殊的循环神经网络(Recurrent Neural Network, RNN)模型[10],时间序列在传统的卷积神经网络中无法被处理,而RNN在长期的时间序列任务上会出现梯度爆炸和梯度消失的问题。LSTM的出现较好的解决了RNN在时序数据长期依赖性预测的问题。LSTM相较于RNN在其结构上新增了门限,具体包括遗忘门、输入门和输出门,这些门限有选择的让信息进行记忆和遗忘[11]。LSTM网络神经元结构如图1所示。
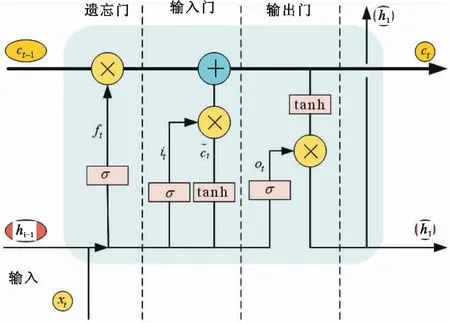
图1 LSTM网络神元结构
每个神经元具有独特的门结构[12]用于维持和控制状态,同时接收两个输入,即上一时刻的输出值ht-1和本时刻输入xt,两个参数首先进入遗忘门,得到决定舍弃的信息后再进入输入门,得到重要信息以及当前时刻的神经元状态,最后由遗忘门和输入门的输出值进行组合,得到分别的长时和短时信息,最后存储操作即下一个神经元的输入。遗忘门公式如公式(3)所示:
ft=σ(Wf·[ht-1,xt]+bf)
(3)
输入门及t时刻的神经元状态方程如公式(4)~(6):
it=σ(Wi·[ht-1,xt]+bi)
(4)
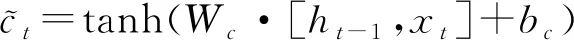
(5)
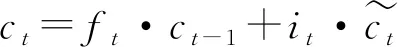
(6)
输出门公式如公式(7)~(8):
ot=σ(Wo·[ht-1,xt]+bo)
(7)
ht=ot·tanh(ct)
(8)
本文所用的BiLSTM模型是在LSTM基础上增加了反向LSTM,由前向LSTM和后向LSTM组合而成[13],它可以通过同时处理过去和未来的信息来更好地理解序列中的上下文,两个单元的输出将被拼接在一起,形成最终的输出。因此BiLSTM在时间序列预测任务中具有更强的建模能力。在模型训练阶段,BiLSTM可以利用前向和后向的信息对的时间序列进行建模,预测阶段直接输出前向LSTM的结果。BiLSTM模型结构图如图2所示。
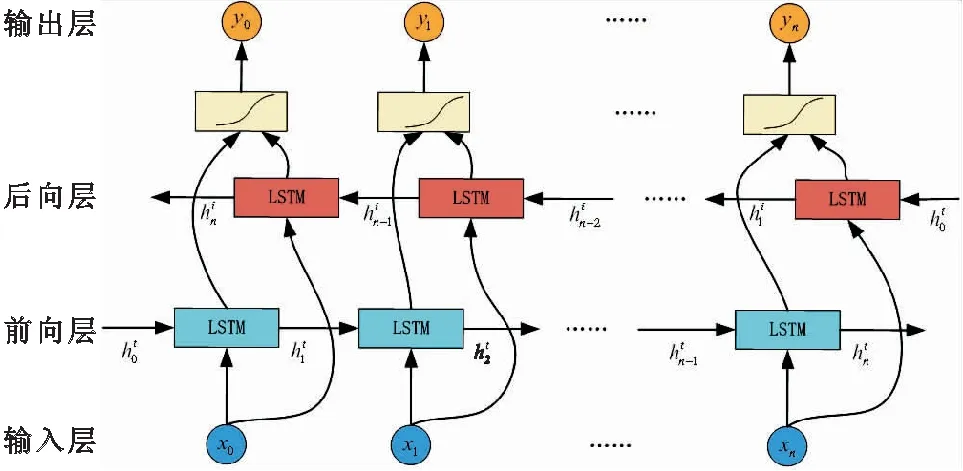
图2 BiLSTM模型结构图
BiLSTM每一级隐藏层状态组合过程如公式(9)所示。
(9)

2 出铝量预测模型构建
本文搭建的模型主要分为三个部分,数据特征提取与数据划分、模型隐藏层、预测输出层,模型训练过程如图3所示。首先进行数据分析和清洗删除缺失过多的特征列,将原始的数据进行相关性析,对数据进行MinMaxScaler标准化公式处理,标准化原理如公式(10)所示。

图3 模型结构图
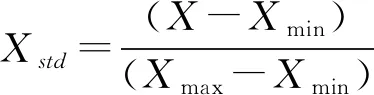
(10)
式中:Xmax、Xmin为数列的最大值和最小值;Xstd为最终的规范化数值。本文采用的是归一化处理。
对BiLSTM模型的批尺寸、网络层数和学习率进行调优。寻找较优的超参数组合,进行模型的训练,Adam优化器进行权值更新,ReLu激活函数提高函数计算能力,DropOut防止过拟合,训练Loss为平均相对误差(MSE),以获取最小Loss值为目标对模型进行训练和优化。
训练好的模型对划分的测试集数据进行预测,并对数据进行逆变化操作,输出预测值。
3 实验分析
3.1 数据清洗
数据采集自贵州某铝厂34台电解槽共120天的槽控机监控数据和人工采集的每日真实铝电解槽生产的日报表数据,共3 814条数据,部分严重缺失数据直接作了删除处理。
搜集到的相关日报和运行参数包括日期、槽号、铝水平、氧化铝浓度、电解质水平、电解温度、分子比、电解温度、氟化铝下料量、平均电压、设定电压、工作电压、下料间隔(设定NB)以及出铝指示量等23项重要信息。通过分析和观察分子比,阴极压降和氧化铝浓度数据缺失过多,因此后续模型建模和训练不再考虑这三个参数。
表1列出搜集到的部分数据。

表1 厂区内某电解槽连续5天收集的日报表数据
3.2 相关性分析
为了体现基于RF的特征选择在电解槽出铝量预测问题上的优越性,本文将Pearson相关性分析法作为对比。此次相关性分析将电解槽出铝量作为被解释变量,其他特征作为解释变量。
3.2.1 Pearson相关性分析
首先利用Pearson系数对所有变量进行划分得出解释变量对于被解释变量的影响系数的排序结果,选取影响系数较高的前六位解释变量。Pearson相关性分析结果如图4所示。
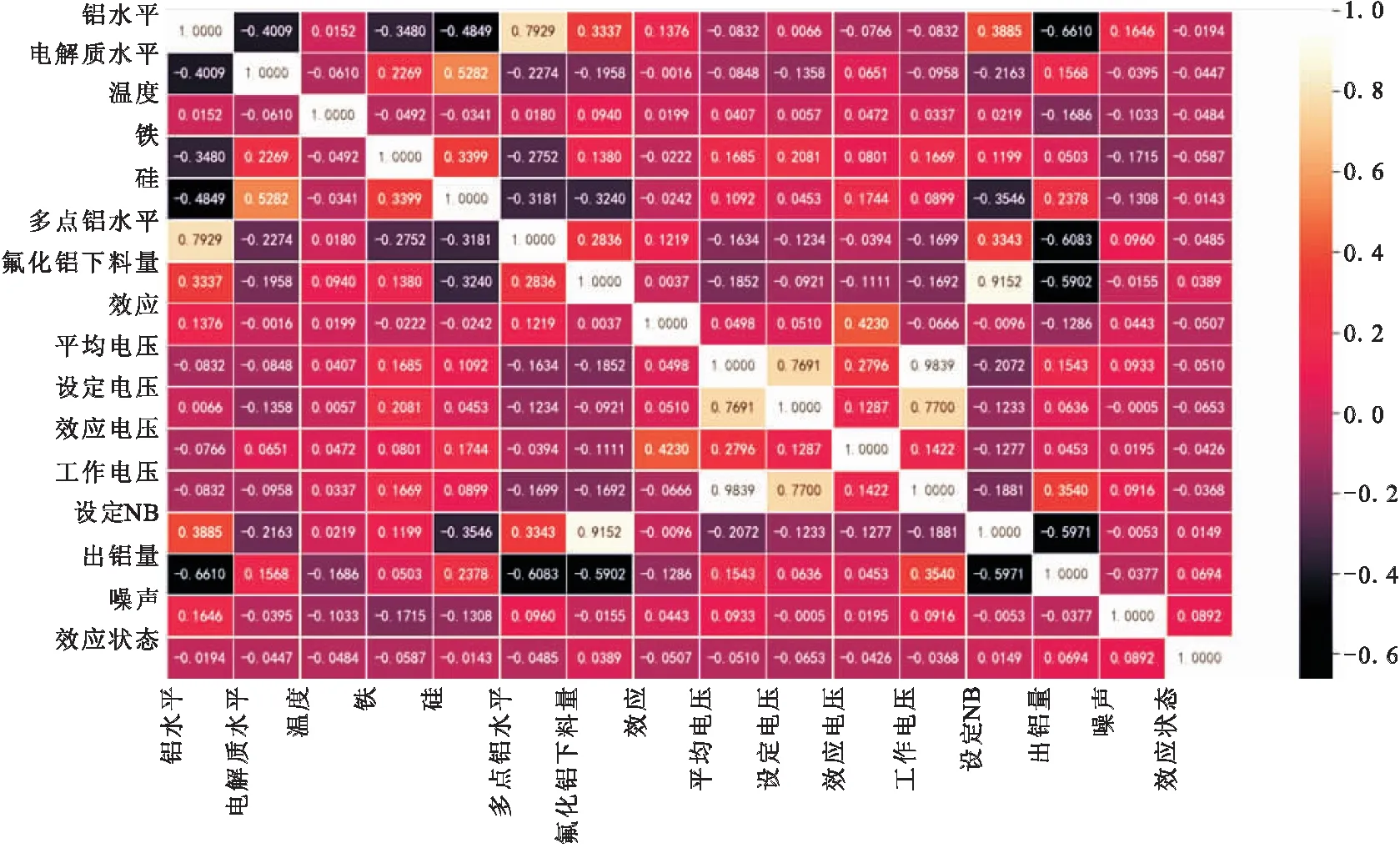
图4 Pearson相关性分析结果
由于Pearson相关性分析只能通过分析出铝量和某个特征(两者)之间的线性关系,也无法确定更高维度特征的因果关系,出铝量的影响分析涉及复杂的非线性因果关系,为了增加特征选择的可对比性,本文采用Pearson特征选择的结果影响系数较高的前六位解释变量:铝水平、多点铝水平、氟化铝下料量、设定NB、工作电压以及硅作为后续模型的输入特征。
3.2.2 随机森林相关性分析
森林进行特征重要性分析出相关系数得分热图,结果如图5所示。

图5 随机森林相关性分析结果
相对于Pearson特征选择,随机森林特征选择可以更好的捕捉出铝量与其他特征之间的非线性关系,也可以同时考虑高维特征数据数据之间的因果性。根据随机森林的分析结果,选取影响系数较高的前六位解释变量:氟化铝下料量、铝水平、温度、设定电压、工作电压以及电解质水平作为后续模型的输入特征。
3.3 超参数调优
考虑到模型的超参数会对模型训练效果和速度产生影响。本文对针对模型的批尺寸,网络层数采用了网格化搜索的方式进行优化。训练设置为200轮,神经元个数为128,为了简化训练避免模型损失过早收敛,设置了早停机制(模型训练10轮后评价指标没有优化就停止训练),通过实验结果选择较优的超参数组合。
3.3.1 批尺寸调优
批尺寸(batchSize)是每次输入进模型的时间序列长度,是模型每次运算的数据大小以及数据之间关联的程度反应。batchSize决定了梯度下降的方向,过大容易导致梯度局部最优解,过小导致模型收敛时间漫长,影响模型的训练精确性。合适的batchSize可以为模型带来有效的提升。因此为研究不同batchSize对模型的影响,本文采取三种不同的取值方式,分别对比了24、48和64的效果。实验结果如表2所示。

表2 不同批尺寸训练结果
三种batchSize在训练结果上相差无几,但是当batchSize为64时,在时间上和效果上略优于24和48,因此本实验模型的batchSize选择为64。
3.3.2 网络层数调优
网络层数(numLayers)越大代表模型的层数越多,模型的拟合能力越强,但是往往越多的层数会带来更复杂的运算,更长的训练时间,同时可能会出现过拟合的现象。因此为研究不同numLayers对模型的影响,本文比较了2、3和4层的效果。实验结果如表3所示。

表3 不同网络层数训练结果
根据试验结果表明三种numLayers在训练结果上,当numLayers为2层时模型在训练效果和悬链速度上均是最优,因此本实验模型的numLayers选择为2层。
3.4 对比分析
为了更好的说明RF-BiLSTM在电解槽出铝量预测问题上的优越性。本文将不同的特征选择(ALL,Pearson)和不同的模型隐藏层结构(RNN,单向LSTM,GRU),来进行对比验证。将数据集按照 6∶2∶2的比例划分为训练集、验证集、测试集。并使用相同的超参数进行了实验。同时为了对比文献[4]以及文献[6]中做的工作,在评价指标中引入了平均绝对误差(MAE),模型训练结果如表4所示。
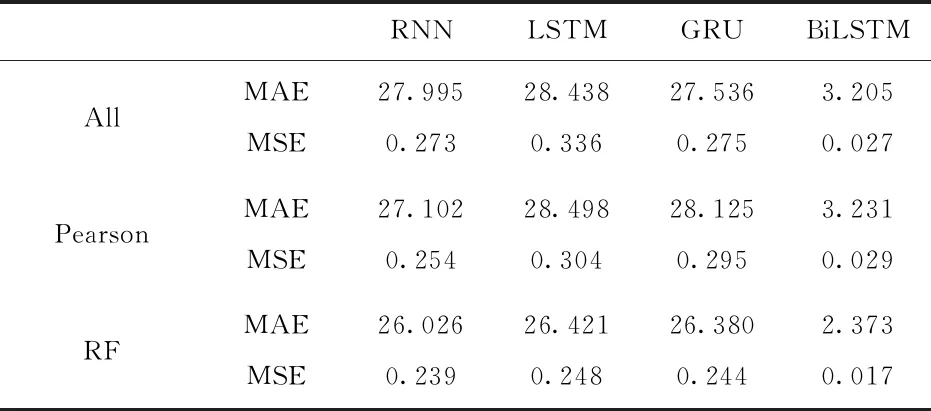
表4 不同模型和特征模型训练结果
根据训练的模型对划分的测试集进行测试,选取了测试集最后50条数据进行绘制预测效果图。各个模型在不同的特征选择下拟合的结果如图6~图8所示,图9展示了BiLSTM模型在不同特征选择下的对比。

图6 全部特征不同模型的预测结果

图7 Pearson特征选择不同模型预测结果

图8 RF特征选择不同模型预测结果
表4展示了不同模型以及不同特征选择之间的误差对比,BiLSTM预测效果要明显优于其他三种结构的模型。其中Pearson特征选择的实验结果在LSTM、GRU和BiLSTM模型上表现不如不做特征选择,RF特征选择在降低了模型特征维度的情况下仍然对模型的训练效果有不同程度的提升。
模型预测结果根据图6~图8显示,RNN、LSTM、GRU和BiLSTM模型都可以在整体趋势上反映出出铝量的变化,而BiLSTM在预测效果上明显优于其他模型。根据图9所示,对比不同的特征选择上的预测效果,基于RF特征选择的BiLSTM在降低特征维度的情况下仍取得了略优于其他两种特征选择 的结果,验证了RF特征选择的有效性。
3.5 适用性考察
为了验证本文提出的电解槽出铝量预测模型可靠性和适用性,本文选择了Pytorch学习框架作为学习模型后端,搭建了在线训练平台,对RF-BiLSTM模型实行了增量化训练,不断根据新的数据进行模型的权值更新,给出一天后的预测结果,给铝厂工作人员提供参考。如图10所示,模型在2726号槽上50条数据进行提前一天的预测结果。
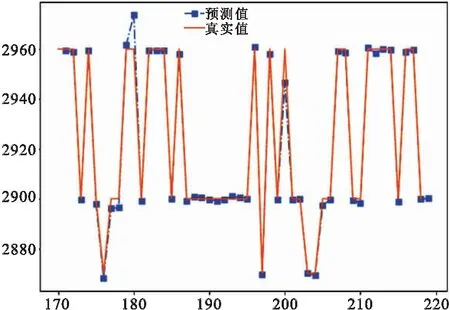
图10 2726号电解槽预测结果
将训练好的模型用于2726号电解槽出铝量预测,输入数据后模型自动计算误差,误差统计后平均绝对误差为4.2,在2726号电解槽上验证了模型的有效性。
4 结 论
1)训练过程中,模型训练的效果受到模型的批尺寸、网络层数的选择所影响,合适的超参数为提高模型的训练效果。本实验提出的RF-BiLSTM以批尺寸为64,网络层数为2层为较优选择。
2)以贵州某铝厂34台电解槽共120天3 814条数据为模型初始训练、验证和测试。对比不同模型的预测效果,RF-BiLSTM平均误差为0.017,平均绝对误差为2.373,优于文献[4]的25.21和文献[6]的35.8。
3)使用RF-BiLSTM电解槽出铝量预测模型在贵州某铝厂的2726号电解槽进行可靠性检验,完成超前一天出铝量预测,预测结果绝对误差在4.2,验证了模型的有效性,实验结果表明RF-BiLSTM在为铝电解槽出铝量预测问题提供了一定的参考价值。
