基于CGKELM 的风功率预测研究

2023-11-03涂菁菁邹伟东

太阳能 2023年10期

赵鹏，涂菁菁*，邹伟东

(1.中国能源建设集团投资有限公司，北京 100022；2.北京理工大学，北京 100081)

0 引言

近年来，中国可再生能源发展迅速、能源结构向低碳化转型的需求迫切，以风光水火储一体化等多种能源相互结合为主体的新型电力系统将成为实现碳达峰、碳中和目标的重要途径[1-3]。发电系统中的风功率预测在解决电力系统供需平衡问题方面起到重要作用，特别是短期风功率预测，在新能源并网、电网运行调度及电力市场辅助服务等方面将发挥更大作用[4-6]。

风功率预测技术研究内容主要包括数值天气预报、风功率转换模型、预测功能应用及预测性能评价，研究方法包括统计方法和物理方法两大类[7-8]。其中，统计方法又可分为时间序列法、人工神经网络法、机器学习法及小波分析法等。比如：文献[9]以风电场的历史数据为基础，利用主成分分析法对天气预报数据进行降维，运用人工神经网络进行特征提取和数据拟合，从而建立风功率预测模型；文献[10]基于主成分分析法提取风功率序列的主成分，对风速信息进行谱聚类，以实现样本信息降维；文献[11]通过对原始信号按频率进行分解重组，并检测熵值对异常分量进行剔除，然后建立核极限学习机(kernel extreme learning machine，KELM)模型进行短期风功率预测。上述各类风功率预测方法通过不同的数据处理方法来提高样本数据的质量，从而达到提高风功率预测精度的目的。但上述预测方容易引入新的参数，参数的设置对模型预测精度有不同程度的影响。

为了更好地提高风功率的预测精度，常利用粒子群优化(particle swarm optimization，PSO)算法、遗传算法、随机森林算法等对支持向量机(support vector machine，SVM)、KELM 等人工智能(artificial intelligence，AI)算法进行参数寻优。比如：文献[12]通过PSO 优化KELM 的正则化系数和核参数，从而提出了一种基于粒子群优化核极限学习机(particle swarm optimization kernel extreme learning machine，PSOKELM)的风功率预测方法。文献[13]通过引入改进自适应遗传算法对BP 参数进行寻优，建立基于小波变换的改进BP 神经网络风功率组合预测模型。文献[14]通过改进萤火虫算法对最小二乘支持向量机(least square support vector machine，LSSVM)参数进行寻优，以降低LSSVM 参数选择的盲目性。但上述用于优化参数的算法存在训练速度慢、耗时长、参数设置复杂等[15]问题。

近年来，风功率预测逐渐由机器学习向深度学习发展，但深度学习自身特点决定了所建立的模型通常具有多层网络结构，并且需要大量数据进行训练，对训练样本质量和仿真计算硬件条件要求较高，更适合进行中长期风功率预测。而共轭梯度(conjugate gradient，CG)法计算速度快、稳步收敛性好，参数设置简单。KELM 学习速度快，能够避免陷入局部最优，泛化能力强[16-17]。在短期和超短期风功率预测方面，能够同时满足对预测精度和训练时间的要求。

因而，针对短时风功率预测应用场景，本文提出一种基于共轭梯度核极限学习机(Conjugate gradient kernel extreme learning machine，

CGKELM)的风功率预测方法。该方法利用CG法优化KELM 的输出权重，以风速作为输入、风功率作为输出，分别建立训练样本和测试样本，进行风功率预测。采用均方根误差(RMSE)、相对标准差(RSD)作为预测精度评价指标。利用某风电场实测数据进行仿真，并将预测结果分别与BP神经网络、LSSVM、KELM 和PSOKELM 的预测结果进行比较，从而证明CGKELM 的有效性。

1 CGKELM 算法

1.1 算法理论分析

梯度法又称最速下降法[18]，其优化思路是将当前位置的最快下降方向作为搜索方向，即当前位置的负梯度方向。本文采用的CG 法是梯度法[19]的一种，该方法是求解正定系数矩阵线性方程式(1)的一种迭代方法，而求解方程式(1)本质上是求二次函数(式(2))的极小值，即相当于求解无约束的凸二次优化问题(式(3))。CG法通过对当前点的负梯度方向和前面搜索方向进行共轭化，从而产生当前点的搜索方向。

式中：A为系数矩阵；b为矩阵和向量的乘积；x为变量的向量；t为转置。

变量的向量的其迭代式为：

式中：k为迭代次数；dk为搜索方向；αk为迭代步长，表示为：

式中：gk为第k次迭代的梯度。

本文采用FR[20]CG 法，从而有：

式中：ηkFR为修正项系数，记为：

1.2 算法流程

与传统神经网络相比，KELM 通过核函数实现一种稳定的核映射，非线性拟合能力更强，能够保证在获得更好或相似的预测准确度的前提下，实现更快的数据处理速度[21-22]。对于任意给定的N个样本数量有：

式中：H为网络隐含层输出矩阵；β为连接隐含层和输出神经元之间的权重向量；T为样本对应的输出矩阵。

CGKELM 是一种单隐含层前馈神经网络，文中利用CG 法去优化隐含层与输出层连接权重向量，从而进行优化求解，建立从风速到风功率的非线性映射。因而，连接隐含层和输出神经元之间的权重向量的公式更新为：

KELM 的网络训练输出O可表示为：

网络训练输出到样本对就的输出矩阵T的误差ε的函数可表示为：

式中：tr为矩阵的迹。

CGKELM 算法流程，如图1 所示。

图1 CGKELM 算法流程图Fig.1 Flowchart of CGKELM algorithm

2 仿真预测实验

2.1 基础数据选取

以某50 MW 风电场的实测数据为例，分别对单点位和整场风电机组数据进行风功率预测，不同方案下的样本数量如表1 所示。单点位方式时，从风电场中随机选择3 台额定功率为2 MW的风电机组，采样时间间隔为15 min，利用前3天的历史数据作为训练样本，对模型进行训练，对第4 天的风功率进行预测。采用整场方式时，则是选取整个风电场的全部25 台风电机组数据用于训练和测试。

2.2 实验结果分析

实验数据采用RMSE 和RSD 进行预测精度评估。均方根误差的计算式为：

式中：eRMS为RMSE；N为样本数量；y(i)为实测平均值；y*(i)为预测平均值。

RMSE 值越小，说明预测精度越高。

相对标准差的计算式为：

式中：dRSD为RSD；分子分母均是标准差形式；为预测值的平均值。

RSD 值越接近1，说明预测精度越高。

两种方案下，分别根据不同样本量对所提出的CGKELM 模型及其他模型进行训练，得到两组仿真结果，分别如表2 和表3 所示。

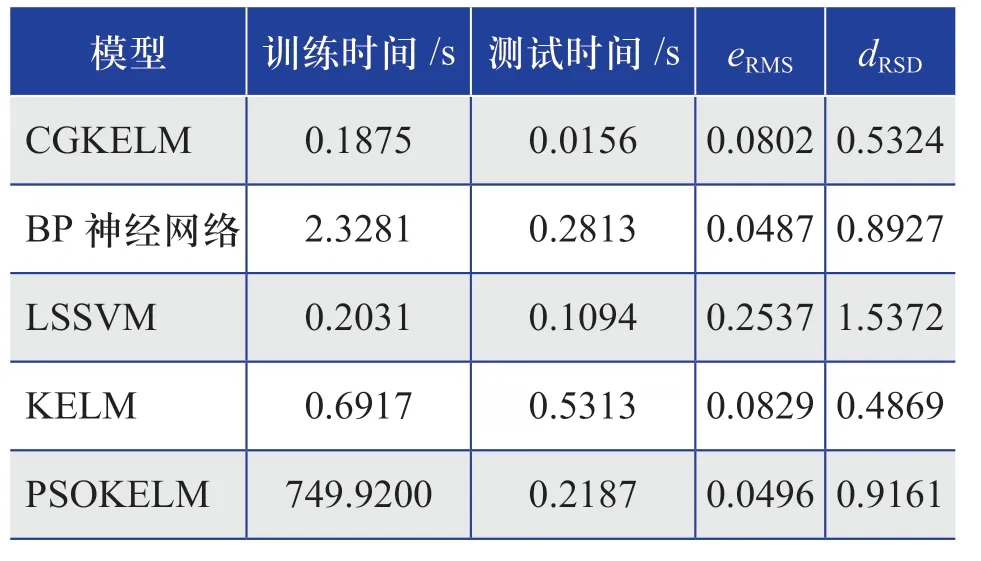
表2 采用方案1 时得到的仿真结果Table 2 Simulation results are obtained by using scheme 1

表3 采用方案2 时得到的仿真结果Table 3 Simulation results are obtained by using scheme 2

通过分析表2、表3 可以发现：CGKELM在训练时间方面具有优势，PSOKELM 和BP 神经网络在预测精度方面效果更好。当样本量比较小时(方案1)，CGKELM 的训练时间分别比BP神经网络和LSSVM 方法快95%和35%；当样本量增大时(方案2)，CGKELM 的训练时间分别比BP 神经网络和LSSVM 快59%和75%，且其此时的预测精度与BP 神经网络的接近。

另外，采用方案1 时，PSOKELM 的训练时间长达12.5 min；采用方案2 时，该模型的训练时间长达10.5 h。这主要是因为引入了PSO 优化KELM 的参数，导致训练时间过长。

为了方便对比分别依据表2、表3绘制柱状图，两种方案下不同方法的训练时间柱状图分别如图2、图3 所示。由图可知，CGKELM 训练时间最短。当样本量由方案1 增至方案2，BP 神经网络训练时间增加了6.3 s，LSSVM 增加了13.9 s。

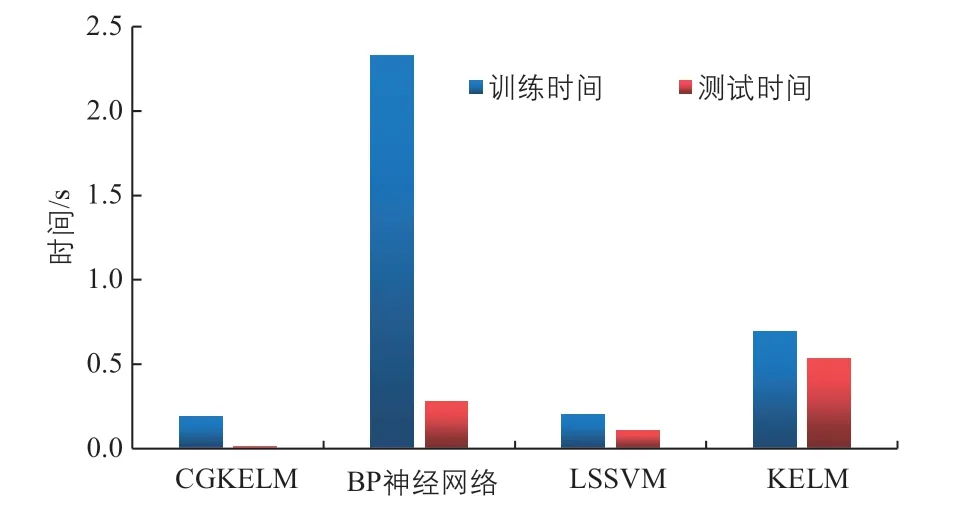
图2 采用方案1 时各种方法的训练时间Fig.2 Training time of various methods with scheme 1

图3 采用方案2 时各种方法的训练时间Fig.3 Training time of various methods with scheme 2

将两种方案下采用不同方法时得到的RMSE和RSD 值绘制成柱状图，分别如图4、图5 所示。根据误差的定义，均方根误差值越小，相对标准差的值越接近1，表示预测效果越好。

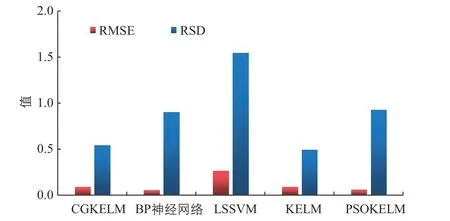
图4 采用方案1 时得到的RMSE 和RSD 值Fig.4 Volues of RMSE and RSD obtained by scheme 1 is adopted

图5 采用方案2 时得到的RMSE 和RSD 值Fig.5 Volues of RMSE and RSD obtained by scheme 2 is adopted

由图4、图5 可知：CGKELM、BP 神经网络、KELM 和PSOKELM 的均方根误差值基本一致，LSSVM 的值最大。PSOKELM 和BP 神经网络的RSD 值最接近1，CGKELM 和KELM 的次之，LSSVM 的RSD 值大于1.5。

综合比较后发现PSOKELM 和BP 神经网络的预测效果更好，CGKELM 和KELM 的次之，LSSVM 的预测效果一般。为了进一步验证预测效果，采用方案1 和方案2 的风功率预测值和实测值对比曲线别分如图6、图7 所示。从图中实测值和预测值的曲线拟合程度可以看出：预测效果与上述误差分析结果一致。