关于“数字信号处理”课程“围线积分法”求z 反变换思政教学的研究和探索

陈兆学，丁佳语，卢永禄

（上海理工大学健康科学与工程学院，上海 200093）

1 引言

由于相关实践探索和教研经验的缺失，目前在理工科实施“课程思政”教学，存在较大的难度，而对《数字信号处理》类课程而言，更是受限于计算机学科的基本特点以及高度抽象、晦涩的课程教学内容，要有针对性地开展“课程思政”，实施起来难度更大和更富有挑战性。

中华民族是一个具有深邃智慧的民族，在漫长的历史发展过程中，积淀了丰厚的文化和科技土壤，诸多精华观点和思想认识具有穿透时空的生命力与前瞻性，即使在计算机信息技术和数字人工智能高度发达的今天，也毫不逊色。如吴文俊院士在中算学思想基础上，跟现代计算机技术和原理相结合，在几何定理自动证明和数学机械化研究方面所取得的相关成果就很说明问题［1］。实际上，在《数字信号处理》教学内容和诸多知识点中，也隐含与中算学有关的内容，从中可以挖掘出与本课程有关的思政元素，以便思政教学的实施。本文作者经过仔细的思考和分析，发现可以在“围线积分法”求z反变换教学过程中以例题的形式把跟贾宪三角形性质有关的思政元素融入进去，对增加课程教学的知识性和趣味性，提高学生的民族自豪感和科技人文相关的综合素养极有帮助。

本文对在“围线积分法”求z反变换教学过程中如何有效融入思政元素进行了研究和探索。论文首先从中算学著名的贾宪三角形及其所隐含的斐波那契序列相关的代数学规律出发，介绍了该序列通项计算表达式的具体特点。然后，基于数字信号处理课程教学中z反变换求取的“围线积分法”法，以例题形式分析了跟斐波那契序列通项公式求取相关的z变换表达式及收敛域的对应关系。在教学中，以例题讲解的形式可巧妙地把相关思政元素融入进去。经过3个学期的教学实践和反馈表明，如此进行思政教学，既可增强“围线积分法”求z反变换教学的趣味性，又可提高学生的学习兴趣和动力，具有良好的教学成效，值得在计算机学科相关教学过程中予以参考和借鉴。

2 贾宪三角形与斐波那契序列及其性质简介

我国南宋数学家杨辉在公元1261年所著的《详解九章算法》一书中提出了如图1（a）所示代数三角形，很多人称之为“杨辉三角”。在上述著作中，杨辉首先介绍了表中除“一”之外的每一个数都等于其肩上两个数之和的递推规律，然后专门注明“出释锁算书，贾宪用此术”，强调指出该方法源出于《释锁》一书所载算术并且已经被北宋数学家贾宪（公元1023—1050年）使用过。因此，更准确地来说，该三角应被称为贾宪三角［2］。另外，如图1（b）相关数码分布规律在欧洲由法国数学家帕斯卡（1623—1662年）首先发现，故有些书上也常被称为帕斯卡三角，但已经比贾宪三角的使用晚了500年左右。元初朱世杰把贾宪三角由七层推广到九层，为高阶等差级数求和高次招差法的发展，提供了有力的数学工具［3］。因此，贾宪三角的发现，对宋元时期中算学的发展有肇基之功，也是对世界数学发展的杰出贡献，值得每一个中国人自豪。

图1 贾宪三角和斐波那契序列

贾宪三角隐含诸多有意思的代数学性质，比如它每一行数字和皆对应2 的整数次幂，而逐行幂次加1，而其斜线上数字和逐层可对应形成著名的斐波那契序列（Fibonacci sequence）即1，1，2，3，5，8，13，21，34，…，如图1（b））所示。

斐波那契序列由大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci）于1202 年在《算盘书》中基于兔子问题得到［4］。其中，他给出的问题如下：“如果每对大兔每月能生育一对小兔，而每对小兔经过两个月后才能长成大兔，那么由一对小兔开始，一年后可繁殖成多少对兔子？”。 当时斐波那契仅仅只是给出了该问题的结果，对斐波那契序列的性质并没有作进一步的探讨与分析，并且在19 世纪初以前，也没有人认真研究过该序列。但随着科技的发展与进步，人们发现斐波那契数列是一个非常特殊而有趣的序列，在自然科学的很多分支中都有应用，如树木的生长、花瓣的数目、植物排列种子的“优化方式”研究、股市变化趋势的预测等，尤其在现代物理、准晶体结构、化学和数学等领域都有直接的应用，甚至还出现在影视作品中，典型如在风靡一时的《达芬奇密码》里它就作为一个重要的符号和情节线索出现。完全可以说，斐波那契序列是一个引起广泛关注和社会兴趣的明星序列，以致于美国数学会从 1963 年起专门出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载相关的研究成果，直至今天。

实际上，斐波那契数列的每一项可基于递推过程生成，其公式非常简单：

而其所对应的通项公式为[5]：

需要强调指出的是，通项公式（2）与著名的黄金分割数φ直接相关，它比较有意思的特点是基于无理数整数次幂之差求出取值为整数的斐波那契序列相应数据项，并且基于该通项公式容易验证斐波那契序列跟黄金分割数的联系［6］

3 基于“围线积分法”求z 反变换方式获得斐波那契序列通项

实际上，有很多方法可以实现斐波那契序列通项的求取［7-9］。有意思的是，可以基于《数字信号处理》课程中“围线积分法”求z反变换的方式来实现通项公式的求取和收敛域的判定，可以通过一个如下例题的求解来实现，即：已知F（z）=z/（z2-z-1），求其z反变换。

基于“围线积分法”实现该例题的求解并不困难（具体方法请参考文献［10］），如下给出简单的求解步骤：

先进行F（z）的零点和极点的求取：零点为z=0，极点为z1=，具体分布如图2所示；

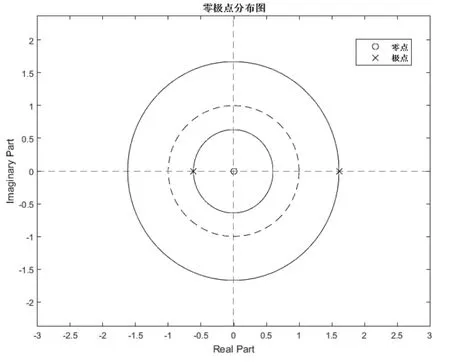
图2 零极点分布图

由于该表达式没有给出具体收敛域，所以需要对其收敛域进行讨论，共有三种可能的收敛域，即：

假设所对应z反变换序列为f（n），则：

（1）当|z| ＞时，f（n）首先为右边序列，且z→ω时，F（z）=0，故f（n）应该为因果序列，故有：f（n）=0，n＜0；当n＞=0 时，zn-1F（z）=zn/（z2-2-1），在收敛域围线内存在两个一阶极点z1和z2，可基于围线积分法求z反变换得：f（n）=此恰为斐波那契序列之通项。此时，有F（z）=z/（z2-z-1）=

n＜=0时，zn-1F（z）=zn/（z2-z-1）分母阶次比分子高2阶或2 阶以上且围线外有一个一阶极点z1，根据围线积分法得：f（n）=-

当n＞0 时，zn-1F（z）=zn/（z2-z-1）在收敛域围线内存在一个一阶极点z2，可基于围线积分法求z反变换得：f（n）=-

（3）当|z|＜时，f（n）为左边序列：

当n＞=0 时，zn-1F（z）=zn/（z2-z-1）在收敛域内无极点，故f（n）=0，当n＜0时，zn-1F（z）=zn/（z2-z-1）分母阶次比分子高2阶以上且在收敛域围线外有两个一阶极点z1和z2，基于围线积分求z反变换得：

f（n）=-恰斐波那契序列每一项相反数。

综上所述，基于“围线积分法”求z反变换方法，该例题在第（1）种情况即收敛域|z|＞时不但可以把斐波那契序列的通项直接计算出来，还给出了其他2种收敛域的具体情况。

4 讨论与分析

因φ=，则对于第2部分中所给出的F（z）=z/（z2-z-1）所对应z反变换的上述三种情况而言，无论其z反变换表达式，还是其收敛域边界，都与黄金分割数φ直接相关。而在第（1）种情况下，当z=2 时又与常数2及其负整数幂次基于斐波那契序列各项的加权和直接相关。这与图1（b）所示类似，实际上以级数展开式的形式进一步揭示了贾宪三角结构中所隐含2的整数次幂序列和斐波那契序列之间所存在的深刻数学关联关系。

在具体实施“围线积分法”求z反变换相关思政教学过程中，可在介绍完基于围线积分法求取z反变换的基本方法和原理后，先将本部分中所给出的例题按正常求取步骤完成求解，随后在分析最后结果时自然而然引出其中所关联的黄金分割数和斐波那契序列，并顺势补充介绍一下黄金分割律在生命、科学、人文等社会各领域所存在的一些具体体现，让学生基本了解黄金分割律的特殊性和普适性，以此吸引他们的注意力并增强课堂学习的知识性和趣味性。最后，基于第1 部分关于斐波那契序列的由来、黄金分割律的性质及其跟贾宪三角形关系相关的历史和背景知识进行铺垫基础上，使得学生在获得相关数学知识点的同时，基于对贾宪三角形相关中国古算学成就及其跟黄金分割律的联系的了解在不知不觉中树立民族自豪感，并对“围线积分法”求z反变换原理和方法附带产生浓厚的学习兴趣和深入把握的冲动，从而能够更能有动机和动力通过自主学习实现对相关知识点的掌握，最终有效改善对示例和相关知识点学习的效果，这对课程学习效率的提高以及进一步增加对本课程整个知识体系学习的兴趣无疑也有帮助。

5 结论

黄金分割作为数学上的一种比例关系，具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值，它在建筑、雕塑、音乐、绘画、运筹学、经济分析等诸多领域有着广泛的应用。同时，黄金分割也是一种生命科学现象和生物数学规律。具有科技和人文相交融的特点和优势。斐波那契序列跟黄金分割律关系密切，关于其通项公式的求取，存在多种不同的数学方法。本论文结合数字信号处理课程的相关知识，以斐波那契序列通项公式的获取方法为切入点，给出了“围线积分法”求取z反变换方法的具体示例，不但可以增加课程教学的知识性和趣味性，同时也有助于学生在学习时能够有效开拓视野和思路，培养多基于学科交叉融合实现守正创新的科学研究理念和素养。经过3 个学期的教学实践和反馈表明，如此进行思政教学，具有良好的教学成效，值得在计算机学科相关教学过程中予以参考和借鉴。

致谢感谢上海理工大学健康科学与工程学院医学影像工程研究所各位老师给本文提出的参考意见.