基于机电类比的线-角振动激振器参数辨识

2023-11-03杨建根俞金辉

计量学报 2023年10期

杨建根, 唐波,, 陈伟, 俞金辉

(1.中国计量大学计量测试工程学院，浙江杭州 310018；2.宁波水表(集团)股份有限公司，浙江宁波 315033)

1 引言

近年来,随着微机电系统(MEMS, micro-electro-mechanical system)惯性传感器的迅速发展,用于MEMS惯性传感器校准的激振器也受到了人们的关注,并对激振器的输出性能提出了更高的要求[1～3]。传统的传感器校准方法多用电磁式激振器[4],而相对于单轴振动激励,线-角复合振动激励更能真实地模拟实际的动力学环境[5],为了满足复合振动传感器校准的需求,需要1种电磁式线-角振动激振器。由于激振器的承载范围、工作频段、激励幅值、输出波形等动力学性能直接影响传感器的校准精度,因此对激振器进行动力学分析显得尤为重要[6,7]。而动力学模型参数是准确分析激振器振动系统动力学特性的基础,所以对电磁式线-角振动激振器进行动力学参数辨识具有重要的科学价值和工程意义[8,9]。模态分析是对机械结构进行参数辨识的1种重要方法,通过建立结构的模态模型,结合实验可实现对结构动力学参数的辨识[10]。温青等[11]通过强迫振动实验对一座双层曲线斜拉桥进行了模态识别,根据不同激励下的频率响应曲线计算模态参数。宋宏伟等[12]采用基于振动实验数据的模态参数辨识方法对振动实验中的集中质量机械系统进行参数估计。但电磁式线-角振动激振器的结构比较复杂,分析过程较为繁琐。由于电磁式激振器具备力学和电学系统,而机械系统和电学系统在本质上具有相同的数学模型,利用机电类比理论对复杂的激振器振动系统进行分析,可使分析过程大大简化[13]。对于将机电类比应用于参数辨识的研究,Saraswat A等[14]针对电磁振动筛系统中存在的非线性问题建立了集总参数模型,并基于机电类比建立了电磁振动筛的参数辨识模型。Tiwari N等[15]基于电磁式单轴振动台的集总参数模型,在对其进行模态分析的基础上结合机电类比原理建立了振动台关键参数的辨识模型。

传统的参数辨识方法大多应用于单轴振动系统研究,而复合式线-角振动激振器在输出线-角复合振动激励时会产生耦合振动,目前关于耦合振动参数的辨识问题研究较少。为此,本文提出了一种电磁式线-角振动激振器参数辨识的方法,可获取该激振器单轴和耦合振动的动力学参数。首先,建立激振器单轴和耦合振动的运动微分方程。其次,基于导纳型机电类比原理建立含力学参数的单轴和耦合振动机电类比模型。最后,根据机电类比模型建立含动力学参数的阻抗公式,结合附加质量法得到其动力学参数的辨识模型。

2 电磁式线-角振动激振器动力学建模

2.1 电磁式线-角振动激振器结构组成及工作原理

电磁式线-角振动激振器的结构如图1所示,该激振器主要由运动部件、磁路组件、线圈组件、复位组件和支撑组件5个部分构成。其中运动部件由工作台、线圈骨架和线圈组件组成;磁路组件由外磁环、内磁芯、第1永磁体和第2永磁体组成;线圈组件由圆周部线圈和轴向部线圈组成;复位组件由支架和弹性绳组成;支撑组件由底座和行程式直线轴承组成。

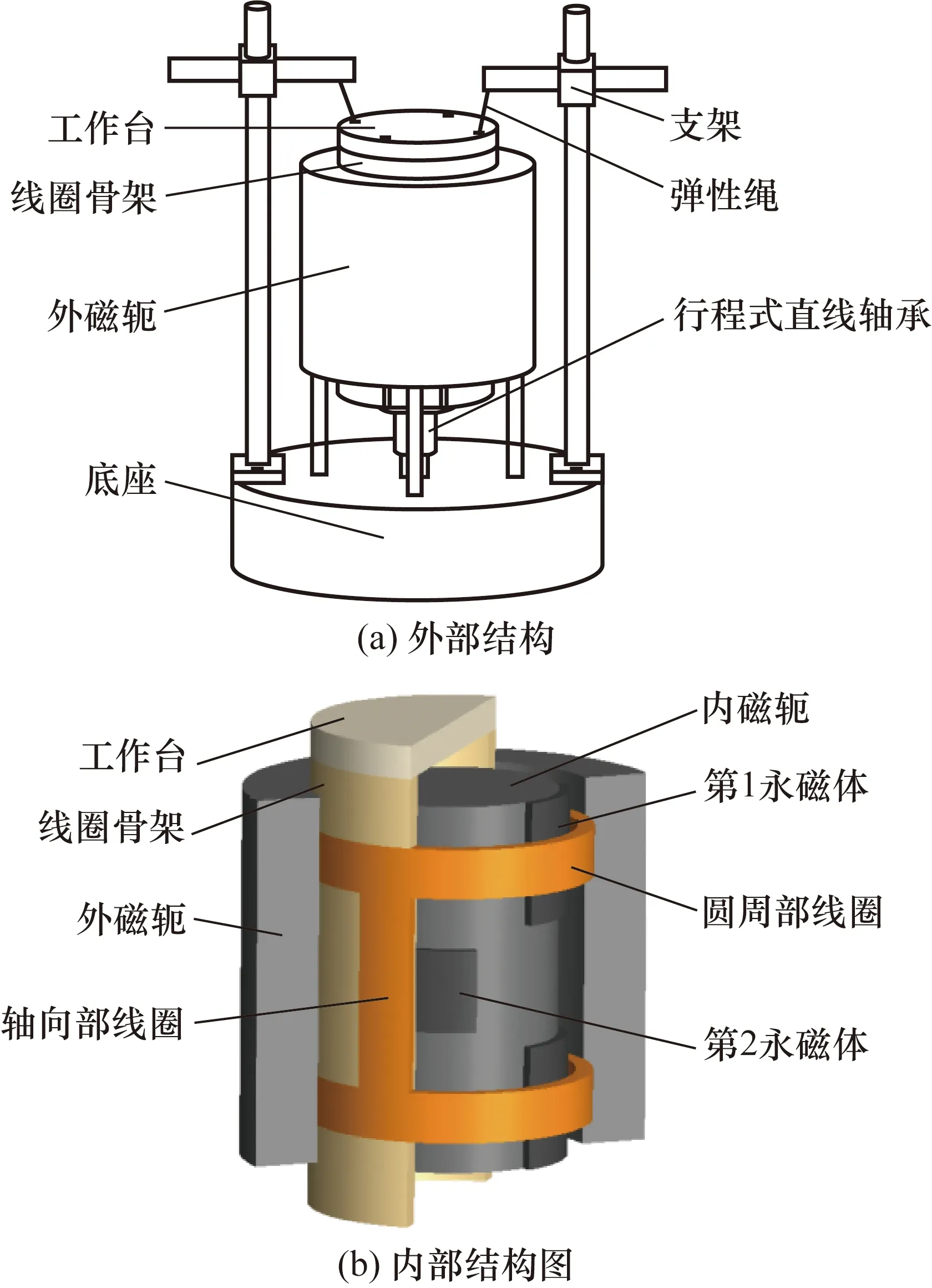
图1 电磁式线-角振动激振器Fig.1 Diagram of electromagnetic linear-angle vibration exciter

磁路组件中内磁芯位于外磁环内,与外磁环一起安装在底座上;永磁体吸附在内磁芯外部,其中第1永磁体和第2永磁体可独立或一起安装,当第1永磁体或第2永磁体独立安装时,永磁体可与内外磁轭形成单轴向的线振动或角振动气隙磁场;当第1永磁体和第2永磁体一起安装时,可与内外磁轭形成线-角复合振动气隙磁场。

运动部件插入内磁芯与外磁环之间通过弹性绳与支架相连抵消自身重力,行程式直线轴承与线圈骨架底部连接,为运动部件提供径向支撑;工作台置于线圈骨架上方,与线圈骨架视为刚体一起运动,传感器可安装在工作台上进行校准;线圈组件嵌入到线圈骨架中,当线圈组件通入正弦交变电流时,运动部件可输出正弦变化的线振动、角振动以及线-角振动同步输出。

2.2 集总参数模型

线-角振动激振器是1种多轴振动系统,需要多个振动微分方程来描述它的运动。为了方便分析,将复杂的分布参数模型简化成集总参数模型,通过集总参数模型来描述该激振器的运动[16]。

在单轴振动方面,该激振器可通过设置永磁体,使运动部件产生单轴向的线振动和角振动,其中运动部件通过复位组件与底座相连,复位组件与底座之间采用螺栓连接可视为刚体,则可将该激振器简化成运动部件和台体(复位组件和底座)2部分。对2种振动模式分别建立集总参数模型如图2所示,其中图2(a)为线振动集总参数模型,Mb为台体质量;kb为台体等效刚度;cb为台体阻尼系数;xb为台体的位移变化;Mx为运动部件质量;kx为运动部件刚度;cx为运动部件阻尼系数;x为运动部件的位移变化;F为线振动激励力。图2(b)为角振动集总参数模型,Jr为台体等效转动惯量;kr为台体等效扭振刚度;cr为台体扭振阻尼系数;θr为台体转过的角度;Jt为运动部件等效转动惯量;kt为运动部件扭振刚度;ct为运动部件扭振阻尼系数;T为角振动激励扭矩;θ为运动部件转动角度。

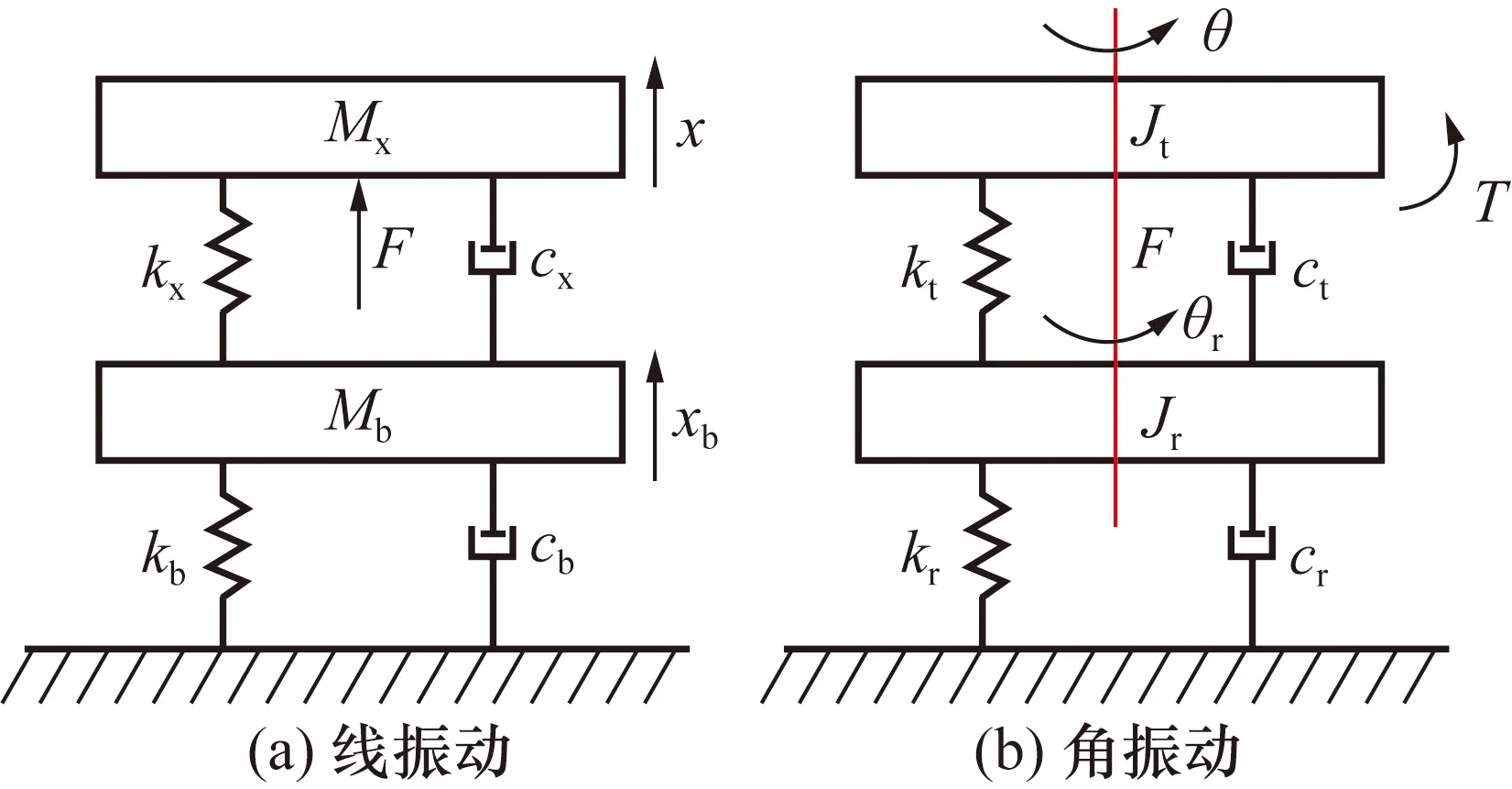
图2 振动集总参数模型Fig.2 Lumped parameter model of vibration

由于台体的质量和转动惯量较大,线圈提供的激励不足以使其产生运动,故在分析时可忽略台体部分。根据牛顿第二定律可建立运动部件的线振动微分方程和角振动微分方程:

(1)

(2)

2.3 线-角耦合振动分析

在复合振动方面,该激振器能够实现线-角振动同步输出,而在实际运动状态下,激振器不仅会产生线振动和角振动,还会产生耦合振动,影响激振器的性能,故需要对耦合振动进行分析。

运动部件的扭转变形不论是正向还是反向,都会引起轴向的耦合变形[17]。假设无阻尼条件下耦合刚度为k,耦合刚度的符号定义函数为δ(θ),根据运动部件的角度变化判断轴向恢复力方向,当θ>0时,δ(θ)=1,轴向恢复力为kθ;当θ<0时,δ(θ)=-1,轴向恢复力为-kθ;当θ=0时,δ(θ)=0,轴向恢复力为0,则轴向恢复力可以表示为Ftx=δ(θ)kθ。同理可得扭振恢复力为Txt=δ(θ)kx。

则无阻尼条件下的耦合振动方程为:

(3)

(4)

(5)

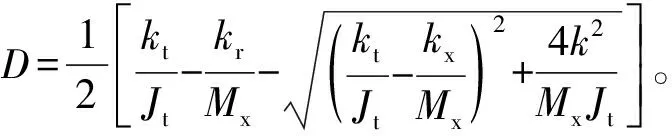
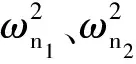
式(3)是1个刚度耦合方程,为了对式(3)进行解耦,令:

(6)

设F=sin(ωxt)、T=sin(ωθt),ωx和ωθ分别线振动和角振动激励的角频率,将式(6)代入式(3)中,方程左右两边乘以ST可得:

(7)

此时方程已完成解耦并实现对角化,进一步求解可得到耦合振动引起的位移和角度响应方程:

(8)

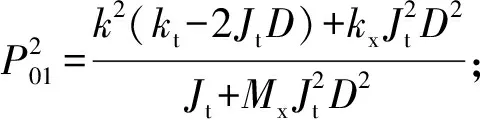
对式(8)进行分析,可得在轴向激励的作用下,耦合出的角度响应取决于运动部件扭角的初始状态,当θ(t=0)=0,即δ(θ)=0时,Δθ=0,说明轴向激励的作用只能产生轴向的振动响应,没有产生扭转振动响应。则当运动部件处于平衡位置,其初始扭角为0时,即理想条件下,耦合振动中扭转振动会产生轴向振动响应,而轴向振动不会产生扭转振动响应。

3 基于机电类比原理的参数辨识模型

3.1 机电类比模型

电磁式线-角振动激振器是1个机电系统,激振器有1个线圈为运动部件提供激励。根据机电类比原理将振动系统转化为电路图,就能用电路分析理论对振动系统进行分析,简化分析过程。根据导纳型机电类比原理将振动系统转化为电路图,将机械系统的动力学参数和电路系统的电学参数进行类比建模,得到单轴向振动机电类比模型如图3所示。

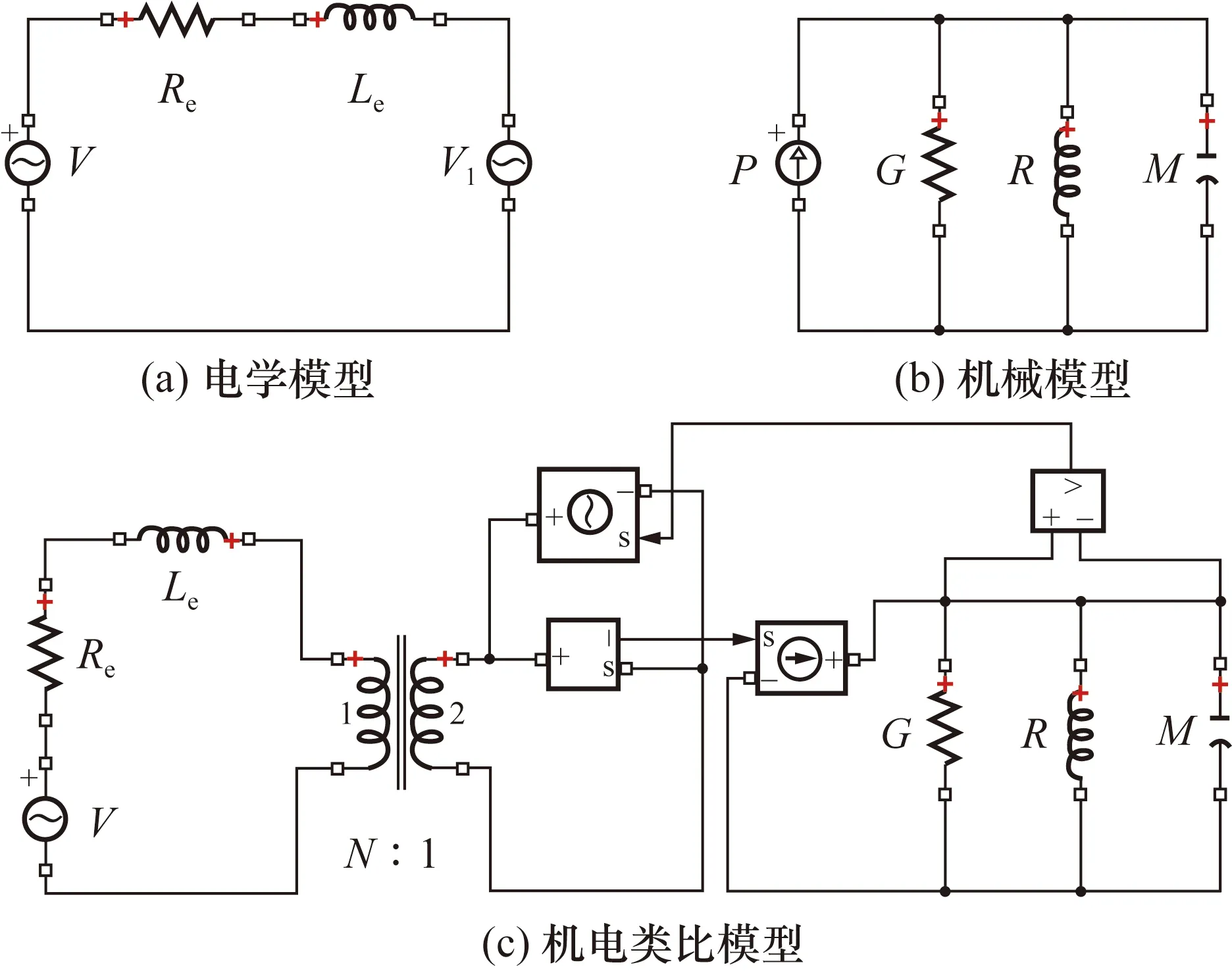
图3 单轴向振动机电类比模型Fig.3 Electromechanical analogy model of uniaxial vibration

3.2 单轴向振动参数辨识模型

激振器的动力学参数可以通过分析激振器在共振频率周围的响应来确定。图3(c)可简化为如图4所示模型。

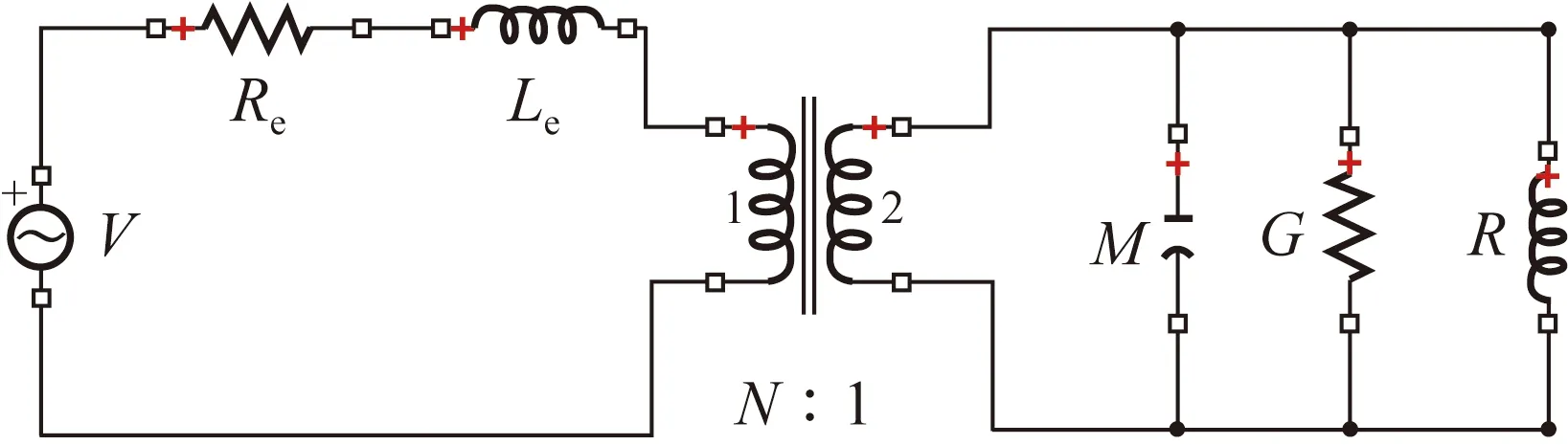
图4 单轴向简化模型Fig.4 Uniaxial simplified model

图4中线圈电感Le提供的阻抗与Re相比很小可忽略,由此可建立阻抗公式:

(9)

(10)

(11)

为了获取力因子N,需要测量该激振器线振动模式下线圈中的电流I以及运动部件的线加速度信号A。根据安培力公式F=IBL,得到线振动力因子N1的计算公式如下:

(12)

对电压、电流以及加速度信号进行FFT分析可得到共振频率下的阻抗值,由阻抗公式可知,当运动部件处于共振频率时,阻抗虚部为0。则在阻抗、力因子以及电阻的参数值已知的情况下可得到阻尼cx的计算公式为:

(13)

线振动和角振动可共用同一机电类比模型,即可共用同一参数辨识模型。若要计算角振动参数,则需要采集该激振器角振动模式下的实验数据,将角振动模式下的空载和负载共振频率代入式(10)和式(11)可得到角振动的转动惯量Jt和扭振刚度kt,将角振动模式下线圈中的电流和角加速度信号代入式(12)可得到角振动力因子N2,结合式(10)、式(11)、式(12)计算结果,由式(12)可得到阻尼ct。

3.3 耦合振动参数辨识模型

电磁式线-角振动激振器可同步输出线振动和角振动,根据工作原理建立耦合振动等效机电类比模型如图5所示。模型上半部分表示线振动部分,下半部分表示角振动部分。

图5 耦合振动机电类比模型Fig.5 Electromechanical analogy model of coupled vibration

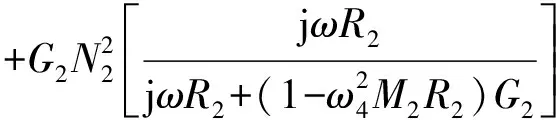
(14)

(15)

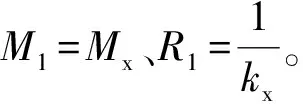
(16)

4 模型仿真验证

4.1 数值仿真算例

本文采用数值仿真算例来验证该方法的有效性,将振动微分方程中的激励简化成以时间t为变量的正弦信号,即F=A0sinωt、T=B0sinωt,其中A0、B0分别为线振动和角振动的激励幅值,ω为角频率。令激励幅值A0=10、B0=0.2,角频率ω=2π,附加标准块质量m=6 kg,转动惯量Jm=0.6 kg·m2,设定该激振器的动力学参数值,根据振动微分方程建立模型进行仿真得到在指定激励下的空载和负载加速度信号,对加速度信号进行FFT分析得到频率响应曲线如图6所示。

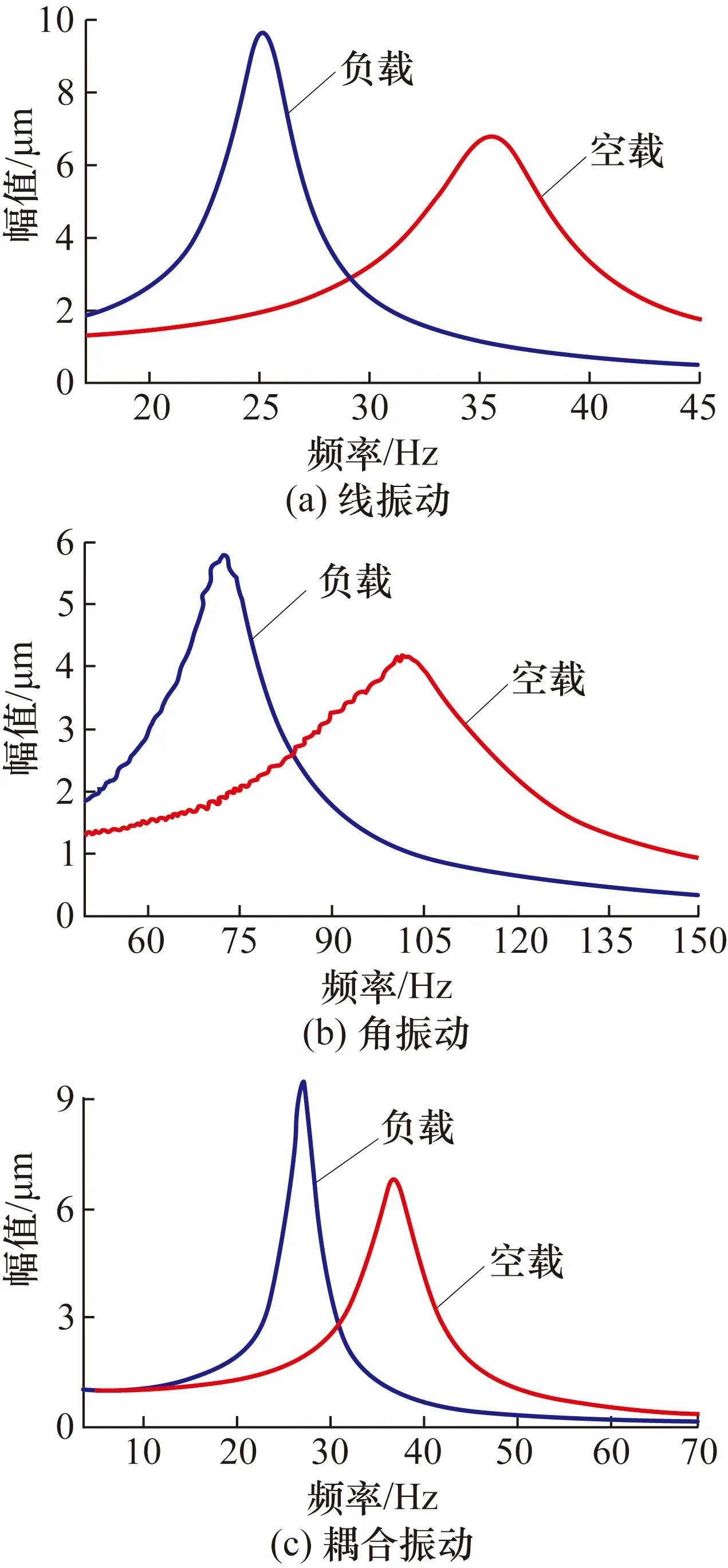
图6 振动频响曲线图Fig.6 Vibration frequency response curve

通过频响曲线图得到相应共振频率转化为角频率如表1所示。

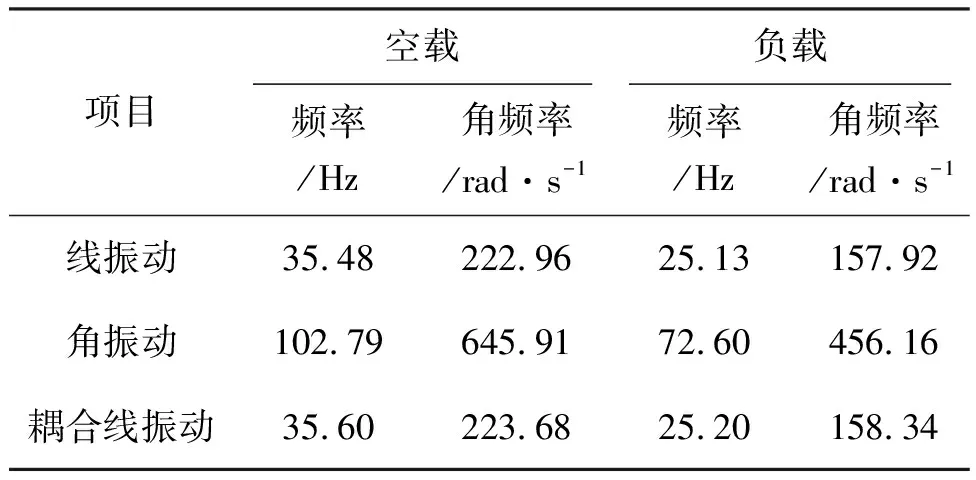
表1 振动共振频率Tab.1 Vibrational resonance frequency

设定电阻和力因子值,令电阻Re=7 Ω,线振动力因子N1=12,角振动力因子N2=0.5,通过建立阻抗模型进行仿真得到线振动和角振动的阻抗-频率图如图7所示。

图7 阻抗-频率图Fig.7 Impedance-frequency diagram

由图7可得在共振频率下,线振动和角振动的阻抗达到最大值,分别为7.718 2和7.002 5。将阻抗值和共振频率值代入参数辨识模型中,得到辨识结果如表2所示。

对比频响曲线图和阻抗-频率图可得,在共振频率下,阻抗达到最大值,这一现象与上文分析一致。并且由表2可得,在指定激励下,由辨识模型得到的参数估计值几乎与给定值一致,各参数的辨识相对误差均在1%以内。由此可见,该参数辨识模型在无噪声环境下能够得到较高精度的参数辨识结果。

4.2 激励源噪声对辨识结果的影响

由于激振器实际工作时输出的信号不免伴随着噪声,为了验证噪声对辨识结果的影响,以线振动为例,在线振动激励源中分别加入信噪比为20 dB和30 dB的白噪声,通过仿真获取不同噪声环境下的共振频率,得到辨识结果如表3所示。通过数值仿真结果可以看出,不论是否加入噪声信号,辨识结果与设定值都吻合得较好,各参数的辨识相对误差均在5%以内。由此可见,该模型在无噪与染噪环境下均能得到较高精度的参数辨识结果。

表3 噪声环境下辨识结果Tab.3 Identification results in noisy environment

4.3 附加质量值对辨识结果的影响

该辨识方法通过在工作台上设置附加标准质量块得到运动部件的空载和负载共振频率,为了验证附加标准质量块参数对辨识精度的影响,设定不同大小的附加质量进行仿真验证。以线振动为例,在原有附加质量m=6 kg的基础上,增设附加质量值m1、m2、m3、m4,其中m1=0.5 kg、m2=3 kg、m3=12 kg、m4=20 kg。通过仿真获取相应的共振频率,得到辨识结果如表4所示。

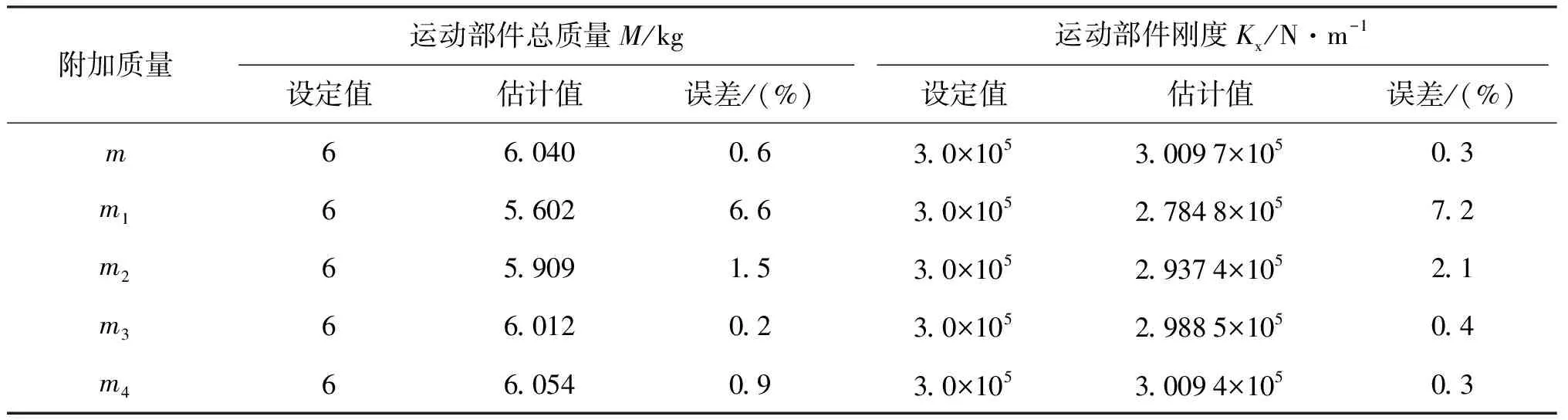
表4 负载环境下辨识结果Tab.4 Identification results under load environment

由表4的辨识结果可知,相较于附加质量为m和m3的辨识结果,m1、m2、m4的辨识相对误差较大,说明附加标准块质量值的改变对辨识精度存在一定的影响,并且附加质量过大或过小都会导致加速度信号的获取和分析难度增大。因此,在能够得到较为清晰的加速度信号的前提下,可选择质量值为运动部件质量1倍或2倍的附加标准质量块。