含SVC 电力系统的IPEBS 法暂态稳定分析*
2023-11-02胡继磊刘雪粲江宁强葛晨阳邱殿成
胡继磊 刘雪粲 江宁强 葛晨阳 邱殿成
(1.国网江苏省电力有限公司连云港供电分公司 连云港 222100;2.国网江苏省电力有限公司徐州供电分公司 徐州 221000;3.南京理工大学自动化学院 南京 210094)
1 引言
为满足远距离大容量输送以及新能源并网发电的要求,静止无功补偿器(Static var compensator,SVC)等基于电力电子技术的柔性交流输电元件在电力系统的应用不断增加,其对电力系统暂态稳定性的影响不容忽视[1]。
SVC 通过改变注入节点的无功功率实现母线电压的动态调节,将其保持在合理区间内,以克服扰动的冲击。在含SVC 电力系统暂态稳定分析研究上,主要包括时域仿真法和直接法。文献[2]提出了一种新自适应逆推方法,并应用到含有未知参数的SVC 的单机无穷大系统,得到了含SVC 单机无穷大系统的自适应规律。文献[3-5]建立SVC 的动态模型,用微分方程描述SVC 的动态过程,并考虑其限幅特性,该模型能实际反映SVC 的动态特征。文献[6]根据短路故障中SVC 导纳变化的显著特征,提出了一种启发式临界清除时间算法,该方法能够提高短路故障暂态稳定分析效率。文献[7]采用Hamiltonian 函数方法,设计了多机电力系统发电机电压调节器和SVC 分散协调控制器。
然而时域仿真法虽能适应复杂的系统,但计算费时。直接法是一种基于能量观点分析电力系统暂态稳定的方法,其优点是能计及非线性,适应较大系统;计算速度快;能够得出稳定裕度[8]。然而如何构造计及SVC 的电力系统暂态能量函数是尚需解决的问题。文献[9-11]以电力系统结构保留模型为基础,构造了计及发电机详细模型、励磁动态和非线性负荷的能量函数,其中,负荷模型的有功和无功可以表示为端电压幅值和相角的任意非线性函数。文献[12]基于SVC 并网母线电压幅值不变,构造了含SVC 的电力系统的能量函数,但没有给出故障后严格单调下降的能量曲线。文献[13]提出了端口能量的概念,证明了端口能量的系统能量是系统的能量函数,并提出了包含风电的暂态能量函数法。
基于等效负荷概念,本文用并网电压和功率表示SVC 势能,构造了含SVC 的电力系统能量函数,并验证了暂态总能量在故障后单调下降的特性;然后采用本文提出的能量函数,运用迭代势能界面法(Iterative potential energy boundary surface,IPEBS)在修改的3 机9 节点系统和10 机39 节点系统算例上进行分析、验证。
2 含SVC 的多机电力系统模型
考虑如图1 所示的电力系统模型,n台发电机,n+m+1 个负荷,第n+1 节点为无穷大母线,发电机发出有功和无功功率分别为gP、gQ,负荷有功和无功功率分别为LP、LQ。SVC 并联在其中某个负荷节点上。
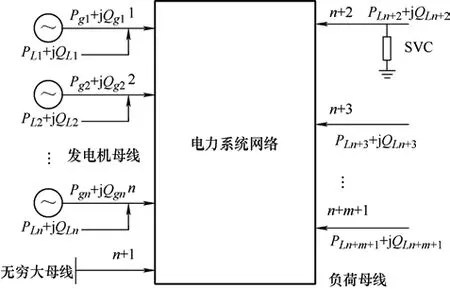
图1 含SVC 电力系统网络
2.1 发电机模型
一般地,对于多机系统中第i台发电机的Eqi′ 恒定模型[8]如下
式中,Pgi、Qgi分别为发电机注入节点i的有功和无功功率;iδ为转子角度;iω为转子角速度;Mi为转子惯性时间常数;Pmi为输入机械功率;iD为阻尼系数;为d轴暂态电抗;xqi为q轴同步电抗;为q轴暂态电势;iV、iθ分别为母线i的电压幅值和相位。
2.2 负荷模型
负荷采用恒阻抗模型
式中,PLi0、QLi0、Vi0分别为稳态时节点i负荷的有功功率、无功功率和节点电压。
2.3 SVC 模型
采用文献[3]中含限幅特性的SVC 模型,如图2所示,SVC 并网母线电压幅值rV为输入量。其动态方程为
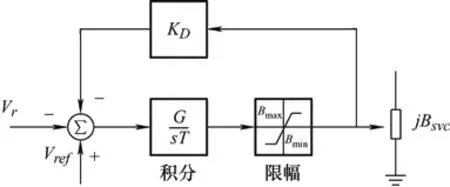
图2 SVC 控制系统
式中,rV为SVC 节点电压幅值;V ref为电压参考值;KD为反馈系数;G为增益;T为时间常数;BSVC0、ΔBSVC分别为SVC 等效基波电纳的稳态值和变化量。
2.4 网络方程
网络节点i的功率平衡方程为
式中,θ ij=θ i-θj,表示节点i和j的电压相位差,QSVCi表示SVC 注入的无功功率。
对于非发电机节点,Pgi、Qgi为0,对于未接SVC 的节点,QSVCi为0。
3 暂态稳定分析
3.1 暂态能量
能量函数W可分为动能函数kW和势能函数Wp两部分,可用如下形式表示
动能kW可以表示为
势能Wp可以表示为
势能Wp由4 部分组成,其中Wg为发电机势能,Wnet为线路势能,WLd为负荷势能,WSVC为与SVC有关的势能。
式(14)中VSVC为与SVC 有关的势能,即SVC 势能。
基于文献[11],本文将SVC 作为等效负荷表示,建立表征SVC 接入电力系统的能量函数。SVC 势能可以表示为
3.2 SVC 能量函数
对于式(15)构造SVC 能量函数,需要求解一个积分方程。但考虑限幅特性的SVC 等效电纳动态过程复杂,且沿故障后稳定平衡点出发到暂态过程运行点的积分路径无法求出[14-15],对于式(15)采用隐式梯形积分法近似求解。
式中,t为时间;h为积分步长。
3.3 能量函数单调性证明
直接法要求能量函数在故障清除后具有单调下降特性,以下证明当WSVC满足式(15)时,能量函数W(x(t))沿着故障后系统轨迹x(t)的导数W˙(x(t))是非正的。
由W(ω,δ,v,θ)=Wk(ω)+Wp(δ,v,θ)可得
综上可得
显然有
3.4 IPEBS 法暂态稳定分析
IPEBS 法是在PEBS 法基础上,增加少量对故障后系统的积分计算,修正临界能量与临界清除时间[16]。
点积判据的符号改变可以表示轨迹是否越过势能边界面,同时也作为IPEBS 法的迭代条件。点积判据如下[17]
式中,Pgi为故障后或故障中投影后的发电机出力;sδ为故障后稳定平衡点的发电机转子角度。
设迭代次数n=0,故障后仿真时间为Ts(本文取5 s)。为防止误判,点积判据阈值为M(本文取10)。计算步骤如下所示。
步骤1:录入系统数据,计算故障前稳态值。
步骤2:计算故障后稳定平衡点。
步骤3:使用时域仿真法积分故障中系统,并将其投影到故障后系统。
步骤4:使用投影后的值计算能量,直至找到势能极大值作为临界能量,从而得到PEBS 法的临界清除时间。
清除故障,对故障后系统积分Ts,并判断点积判据是否大于M,若大于M则转步骤6,否则转步骤7。
步骤6:n=n+1,计算故障后势能,将势能极大值记为,相应的临界清除时间记为。转步骤5。
4 算例分析
本文将所构造的能量函数在修改的3 机9 节点系统和10 机39 节点系统上进行暂态稳定分析,验证其有效性。
4.1 修改的3 机9 节点系统
在修改的3 机9 节点系统用IPEBS 法计算故障临界清除时间,系统单线图如图3 所示,SVC 接母线6。

图3 含SVC 的3 机9 节点系统
4.1.1 算例1:稳定场景
在0.1 s 时刻节点8 发生三相短路故障,持续0.236 s,故障后恢复原系统,系统最终稳定。
图4 为稳定时系统的暂态能量与点积判据。由图4 可知,暂态总能量W在故障中持续增加,故障清除后逐步减小。动能与势能在故障中增大,故障后二者相互转换,由于存在阻尼,极值不断减小。点积判据在故障中与故障后始终小于0,表明轨迹没有越过势能边界面。
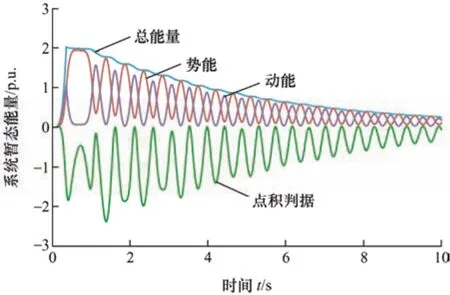
图4 稳定时暂态能量
图5 显示故障后总能量的时间导数是严格负值,满足能量函数单调下降条件。

图5 稳定时故障后总能量的导数
图6a 和图6b 分别为SVC 投影前后的电压幅值和功率,图6c 为SVC 作为等效负荷的能量。电压幅值、功率和势能经振荡后,最终稳定为一定值。从图6b 和图6c 可知,没有发生有功功率交换,计算出的有功势能恒为0。

图6 稳定时SVC 电压、功率和势能变化
4.1.2 算例2:失稳场景
在0.1 s 时刻节点8 发生三相短路故障,持续0.237 s,故障后恢复原系统,系统最终失稳。
图7 显示失稳时,系统动能持续增大,系统势能与系统总能量持续减小。点积判据增幅振荡,远远大于0,表明轨迹早已越过势能边界面。图8 显示故障后总能量的时间导数是严格负值,满足能量函数单调下降条件。图9a 和图9b 分别为SVC 投影前后的电压幅值和功率,图9c 为SVC 作为等效负荷的能量。系统失稳,电压幅值、功率和势能发散。与稳定时一样,SVC 没有发生有功功率交换,计算出的有功势能恒为0。

图7 失稳时暂态能量
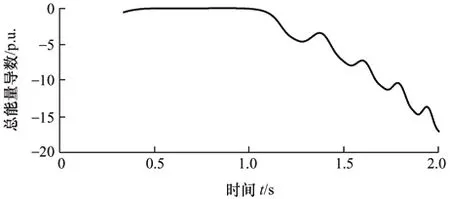
图8 失稳时故障后总能量的导数

图9 失稳时SVC 电压、功率及势能变化
采用本文构造的含SVC 电力系统能量函数,用IPEBS 法计算系统的CCT。表1 给出了时域仿真法(TDS)和IPEBS 法计算得到的CCT。由表1 可见,IPEBS 法得到的CCT 和TDS 法得到的CCT 绝对误差在0.01 s 以内,相对误差小于±10%。
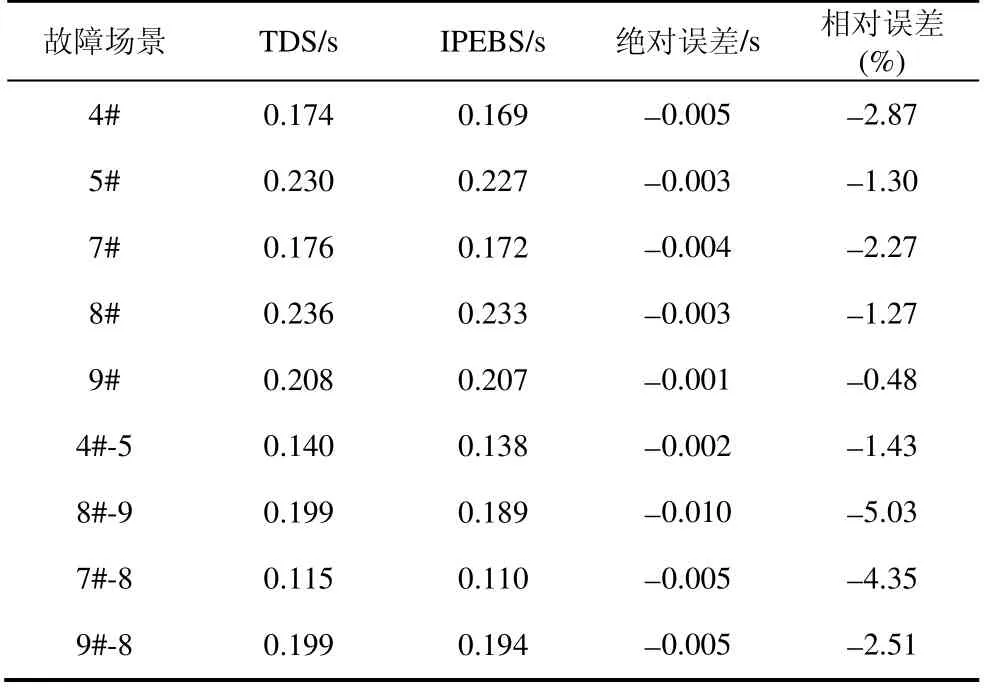
表1 含SVC 的3 机9 节点系统CCT 比较
4.2 修改的10 机39 节点系统
本节进一步对修改的10 机39 节点系统进行暂态稳定分析,在14 节点、26 节点处加装SVC,修改后的系统拓扑结构如图10 所示。
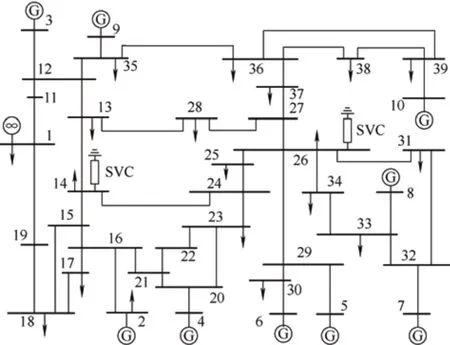
图10 含SVC 的10 机39 节点系统
在0.1 s 时刻,节点20 发生三相短路,暂态稳定和暂态失稳的故障清除时间分别为0.105 s 和0.106 s,图11、图12 分别为系统稳定和失稳时的总能量和SVC 势能的变化情况。
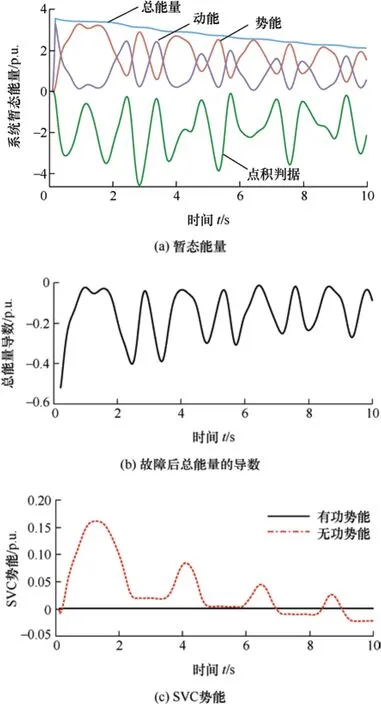
图11 稳定时总能量和SVC 势能变化

图12 失稳时总能量和SVC 势能变化
图11 表明在系统稳定情况下,暂态总能量满足单调下降特性,SVC 势能中的有功势能为0,无功势能最终稳定为某一定值。图12 表明在系统失稳情况下,总能量对时间导数仍小于0,SVC 势能中的无功势能发散,但有功势能仍为0。
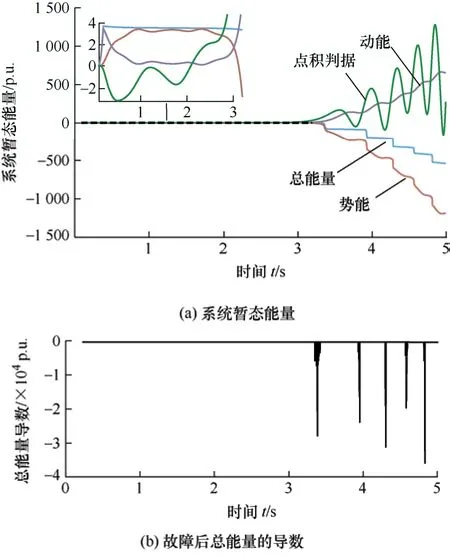
表2 给出了TDS 法和IPEBS 法在不同故障场景下的CCT 结果。由表2 可见,IPEBS 法得到的CCT 和TDS 法得到的CCT 绝对误差很小,相对误差小于±10%。
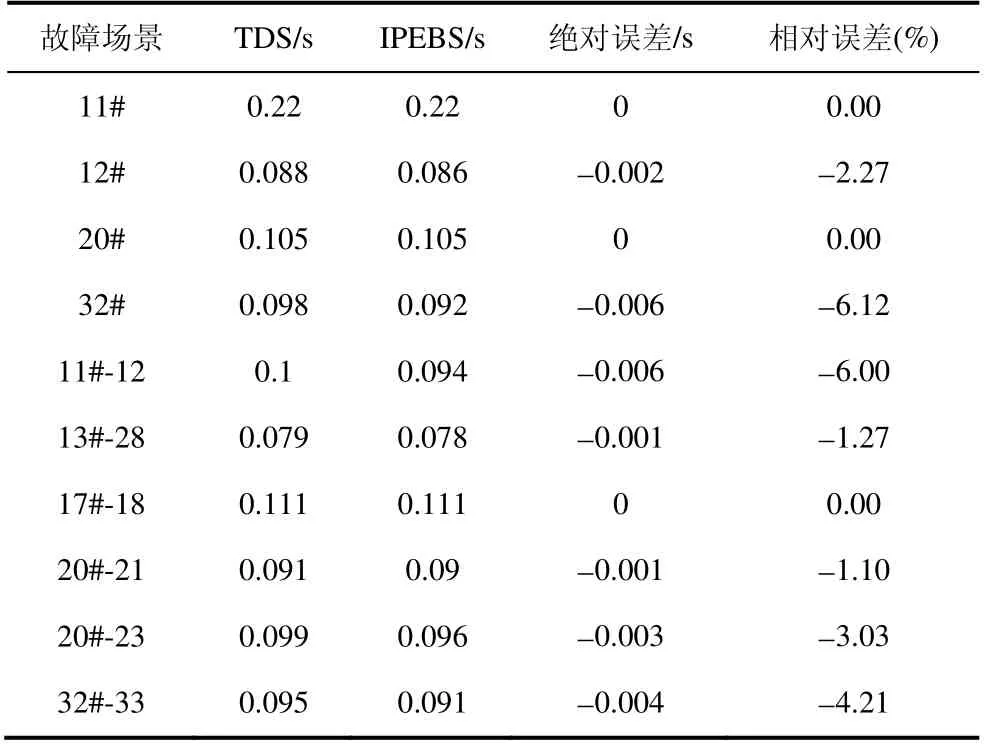
表2 含SVC 的10 机39 节点系统CCT 比较
5 结论
本文基于等效负荷的概念,将SVC 势能用并网点电压和功率表示,构造了含SVC 电力系统的能量函数,获得如下结论。
(1) 证明了构造的能量函数单调下降特性。
(2) 采用本文提出的能量函数,在修改的3 机9节点系统和10 机39 节点系统算例中验证了IPEBS法的有效性。
(3) 计算结果表明,与时域仿真法相比较,所得故障临界清除时间的误差较小,能满足暂态稳定分析的要求。
