雷击降弓过程中机车受流动态特性研究
2023-11-02朱彦锦姚智杰符思雨韦宝泉肖钦文袁佳歆
曾 晗 朱彦锦 姚智杰 李 萍 符思雨 韦宝泉肖钦文 袁佳歆
(1.华东交通大学省部共建轨道交通基础设施性能监测与保障国家重点实验室 南昌 330013;2.湖南工学院电气与信息工程学院 衡阳 421002;3.武汉大学电气与自动化学院 武汉 430072)
1 引言
在过去的十年中,运输需求不断扩大,推动了电气化铁路的发展。电气化铁路的牵引系统在其运营中起着至关重要的作用,铁路事故也时有发生,其中列车受电弓的升降会出现拉弧和电磁干扰,从而导致设备故障和安全隐患[1-4]。2010 年,瑞典曾发生一起降弓燃弧事故,造成短暂停电,无人员伤亡。弓网电弧问题是制约电气化铁道发展的重要原因之一,雷电环境会导致弓网系统短路和拉弧,损坏弓网设备,扰乱列车正常运行[5-6]。同时也有不少学者对降弓运动与机车运行进行研究,发现受热效应影响,降弓电弧对机车高压端设备材料的侵蚀尤为显著[7-9],过分相、降弓过程能量发生振荡,对列车车顶高压设备造成威胁[10-12]。文献[13]使用CFD 流体计算研究了机车静态时降弓电弧稳定燃烧的电气特性,文献[14]运用动网格技术处理机车运行时降弓电弧动态特性与影响因素,文献[15]基于MHD 模型研究了列车运行时风速对降弓电弧特性的影响,但鲜有人关注雷击下降弓过程对机车受流动态特性的影响。因此,研究雷击环境中降弓电弧具有重要意义,能够为了解电弧的行为及其对牵引系统机车运行的影响提供数据分析,有助于制定安全预防措施,以减轻雷击和电弧对牵引系统的影响,保证列车的安全运行。
2 牵引系统弓网电弧仿真模型
2.1 牵引系统弓网电弧模型搭建
2.1.1 牵引系统供电模型
重载列车在行驶的升弓、降弓工况下均可能出现燃弧现象,本文针对重载列车以时速73 km/h 行驶工况下发生弓网离线电弧现象开展分析。我国高速铁路牵引网多采用2×27.5 kV 的自耦变压器(Autotransformer,AT)供电方式,其牵引系统供电模型如图1 所示。
该模型将钢轨视为一条传输线路,使其能够与接触线、正馈线或回流线进行线路间的耦合。基于图1,针对出现弓网离线电弧时的整个牵引网建立等效模型,如图2 所示。基于图2,牵引变电所到负荷之间的牵引网线路采用了分布参数等值模型,由相同、多个π 型等效集总参数模型串联组成。
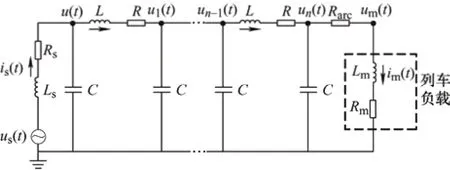
图2 牵引网等效模型
根据牵引网空间分布以及导体参数计算出牵引网电气参数,利用导线合并方法,将5 km 单线牵引网等效为单位长度的T 型电路,然后将其扩展为任意长度的牵引网线路模型。图2 中,牵引网模型由n个R、L、C构成的Ⅱ型部分串联构成,分别代表牵引网给定长度下的等效电阻、电感及电容;Rm、Lm分别为负荷等效电阻与电感;Rarc(t)为电弧等值的非线性电阻模型;Rs、Ls分别为牵引变电所变压器等效电阻和电感;us(t)为牵引变电所母线电压;un(t)为牵引网末端线路电压;um(t)为受电弓弓头输入电压。
2.1.2 牵引系统机车模型
本文选用重型货运机车进行建模研究,其电力原理图如图3 所示。根据图3 所示主电路原理图,主电路仿真的主要组件包括牵引电源、主变压器、整流调压电路、平波电抗器、串励电动机等。其中,整流调压电路采用不对称不等分四段经济半控桥式整流电路。整流电路的晶闸管触发信号来自脉冲发生器模块,而串励电动机采用了一个等效模型来实现,即牵引电机总内阻串联反电动势。
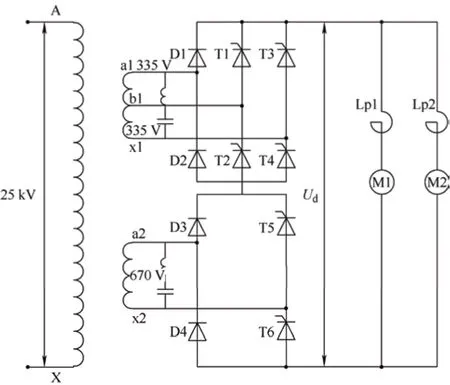
图3 重型货运机车主电路原理图
2.1.3 Habedank 电弧模型
在电弧模型中,由于弓网间电弧的电阻为非线性动态电阻,而电弧模型不仅与牵引网参数有关,还与电弧黑盒模型选取有关。Mayr 等效电弧模型主要适用于电流过零时的小电流情况,而Cassie 电弧模型则适用于电流过零前的大电流燃弧情况。这两种电弧模型单独考虑都有一定的限制。Habedank 等价电弧模型是Mayr 电弧模型和Cassie 电弧模型的结合并加以修正,能较好地反映电弧非线性特性。电弧模型由反馈控制电流源、Fortran 微分编辑器、Slide 整定值、阶跃功能、电压测量等模块组成。电弧模型的实现如图4 所示。
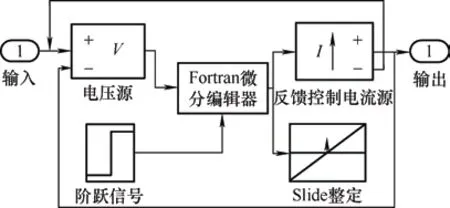
图4 电弧逻辑模块模型
电弧模型的封装模块为实时封装了内部复杂的电气量变化的逻辑电路,其中电弧电导g是由常量系数C、经验系数B以及实时测量的电弧电流i共同决定,将电弧电导g求倒数即可得出电弧电阻r的表达式。电弧模型的封装模块如图5 所示。

图5 PSCAD/EMTDC 电弧封装模块模型
2.2 模型参数设定
2.2.1 牵引系统参数设定
本文讨论了电力系统中使用三相变压器的直接回流供电系统的建模,仿真模拟同一供电臂下单列车的运行情况[16-17]。该系统的参数如表1 所示。建模过程还包括使用模块来模拟变电站和根据表1 定制各种元素参数。建模涉及到集成电压源、脉冲发生器和其他模块的构建,包括电压和电流的多个测量模块。图6 是V/v 变压器的模拟图。

表1 牵引供电系统参数设置

图6 V/v 牵引变压器接线仿真
牵引网架空线模型的构建考虑了接触线、加强线、回流线和铁路轨道的参数。这些参数是根据各条线路参数的相互影响及其空间关系来设定的。图7 显示了架空导线的T 型等效模型模拟。表2 和表3 分别列出了等效线路电路的自电容、自电感以及互电容和互电感的参数。

表2 等值线路自电容自电抗参数表
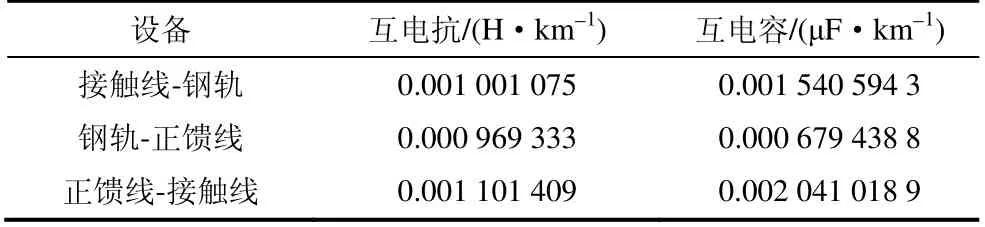
表3 等值线路互电容互电抗参数表

图7 牵引网T 型等效模型仿真
2.2.2 弓网电弧参数设定
本文采用Habedank 模型进行仿真。Habedank模型是基于Cassie 模型和Mayr 模型进行的改进,在PSCAD 中的仿真模型如图8 所示。

图8 Habedank 电弧模型建立
作为用于研究雷击过电压的黑盒模型,需要设置多种输入参数应用于建模中。基于实际测验所得Habedank 具体参数如表4 所示。

表4 Habedank 电弧参数设置
2.3 数学模型
2.3.1 牵引系统模型
(1) 牵引电机电枢电流的确定。重载型机车SS4的牵引控制特性函数如式(1)所示,牵引控制系统的级位和速度共同决定了电动机电枢电流的大小。
式中,v为机车速度,单位为km/h;k为机车挡位,取0~10;Id为电机电枢电流,随速度v和级位变化,电流取式(1)的最小值,单位为A。
(2) 机车晶闸管触发角的大小可以用机车牵引控制特性和整流回路的关系确定。当给定运行级位和机车速度时,根据式(2)可以得出牵引电机的端电压Ud,其中,∑R为牵引电机总内阻。
V/v 变压器原次边电压电流关系表达式为
当机车运行参数、外界条件确定时,可用双傅里叶级数表达
式中,Ma为PWM 变流器的调制系数;δ为采样因子;ωm为调制波角频率;ωc为载波角频率;Jn为第一类的n阶Bessel 函数。2.3.2 弓网电弧模型
在特定假设下,基于能量守恒方程的Cassie 和Mayr 电模型在实际应用中存在一些限制。如果电弧电流过零前的电流较大,使用Cassie 模型更符合实际情况,而Mayr 模型主要适用于电流过零时的小电流。国内外学者主要从两个方面对Cassie 和Mayr模型进行了修正和完善。首先,探究不同电弧阶段所需的合适电弧方程以描述电弧;其次,探究电弧参数的影响因素,以及它们之间的函数关系。其中,Habedank 将Cassie 和Mayr 模型拼接成一个电弧模型,以补充Cassie 和Mayr 模型的缺点,更好地描述真实电弧的非线性动态特性。其数学模型如下
式中,gc和θc为Cassie 电弧模型的电导和时间常数;uc为电弧电压常数;gm和θm为Mayr 电弧模型的电导和时间常数;P0为电弧耗散功率。
电弧的动态数学模型可表示为
令电弧时间常数为τs,可表示为
则有电弧模型的通用数学表达式,根据不同的假定条件对时间常数和散出能量P进行修改,得到所需电弧模型。
得到控制逻辑封装模块电弧模型的表达式为
式中,Gs为稳态电弧电导。
基于基尔霍夫电压定律,通过对实测数据进行拟合得出所需非线性变化电弧电阻的降弓控制方程。
式中,Um为开关闭合瞬间电源电压幅值;R0为电弧基础电阻;λ为速度特性系数;C为电弧耗散功率相关系数。
电弧单位长度耗散功率与降弓速度关系为
标准冲击波雷电流方程为
式中,I0为雷电流幅值;α和β为特性系数。
3 仿真结果分析
采用上述模型,本文对50 Hz 单相交流电供电方式,接触线单位长度1.49 Ω/km,牵引变压器空载电流0.23%,负载损耗为回路阻抗电压比10.5%,电弧时间常数为2 的牵引系统电弧模型进行了仿真,对比传统电弧模型阐述了Habedank 电弧模型的优势;分析了不同倍数雷击电流下降弓过程对机车受流动态特性的影响。
3.1 弓网电弧
本文仿真分析了在牵引系统27.5 kV 供电正常运行时,时速73 km/h 重载列车的弓网电弧特性,将建立的Habedank 综合电弧模型与Mayr 和Cassie两种传统电弧模型进行对比,结果如图9、10所示。

图9 传统模型与Habedank 模型电压对比
由图9 可知,与Mayr 模型相比,Cassie 模型表现出更陡峭的过电压峰值,导致了更严重的瞬变。然而,这两个模型都不包括明显的燃弧电压和灭弧电压。相比之下,综合动态Habedank 模型清楚地显示了燃烧电弧和熄灭电弧,可以更准确地反映真实的电弧特性。Habedank 模型通过电弧本身产生的电压和电流来实现这一点,能够更精确地模拟、分析和预测电弧的影响,如图10 所示。所构建的Habedank 综合动态模型下的电压和电流波形与文献[18]中电弧试验波形一致,说明电弧的特征能够在综合动态模型中得到很好的显示。
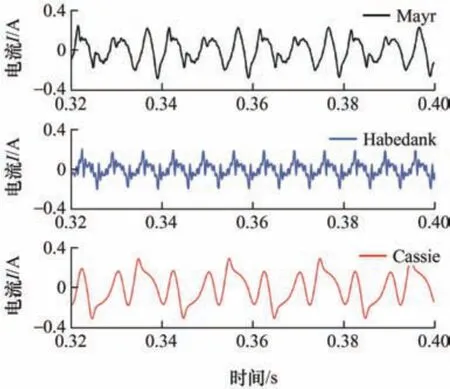
图10 传统模型与Habedank 模型电流对比
3.2 雷击降弓对牵引系统列车运行的影响
当弓网之间产生降弓电弧时,此时的电磁暂态过程是由于接触网电源电压对电缆寄生电容充电导致,等效电路的振荡波动和过电压峰值受到机车高压端设备电感与接触网电源等值阻抗等因素影响。根据文献[19-20],设置雷击电流分别为2 kA、7 kA和10 kA 进行仿真分析。对模型输入幅值为1 kA 的雷击电流为一倍雷击电流,在1.98 ms 时进行燃弧降弓,2.013 ms 时输入雷击电流,对不同倍雷击电流下机车高压端电压的变化进行对比,仿真结果如图11 所示,2.100~2.500 ms 不同倍雷击电流降弓机车功率变化如表5 所示。

表5 不同倍雷电流下机车高压端电压变化

图11 不同雷电流下机车高压端电压
数据表明,在雷击期间,弓网电弧电流振幅随时间发生显着波动,基本呈先增后降的趋势。随着输入雷击电流的增大,重载机车高压端过电压峰值也增大,过电压增长速度也越快。
在雷击开始的0.05 ms,机车高压端过电压呈尖峰状迅速增长,在接下来的0.1 ms 呈减少趋势,再有小增幅后趋于平衡,10 倍雷击降弓的情况下受电弓高压端过电压幅值最大并且变化幅度最大。这是由于电弧作为等离子体非线性行为,在雷击首次形成时,沿等离子体通道的空气分子被电离并迅速加速,电场迅速增加,自由电子密度增加,形成高密度等离子体,随雷电继续流经等离子体通道,等离子体通道的电容变显著,通道的特征阻抗增加,达到最大电阻时过电压达到峰值。在热效应的影响下,机车高压端过电压迅速下降。雷击主要影响的是高压端过电压变化幅值,降弓运动主要影响的是高压端过电压的变化率。
当降弓运动接近过零点时,等离子体通道的长度减少,导致通道的电阻增加,高压端的电流振幅减少。电流变化的速度变慢,从而导致过电压波动的振幅下降。最终在等离子体通道的电容增加和等离子体密度下降之间达到平衡,这种反馈回路导致电弧振荡。由于输入雷击电流增强电场,改变电荷分离与自由电荷速度,与高压端设备电感电容元件共同作用,不同倍数雷击电流的振荡恢复出现不同。
对雷击降弓时机车高压设备端功率情况进行分析,仿真结果如图12 所示,2.011~2.027 ms 不同倍雷击电流降弓机车功率变化如表6 所示。

表6 不同倍雷击电流降弓机车功率变化

图12 不同雷击电流降弓机车功率变化
对图12 所示机车功率变化进行分析,发现机车功率在燃弧降弓后呈现减小趋势,这是因为电弧的降弓运动会导致接触线的电阻增加,等离子体通道的电阻率增加,通道内的电场强度下降,从而使得电流振幅下降,导致机车高压端得到的功率下降。同时,由于接触线和受电弓之间的距离增加,接触线的电阻也会增加,机车受电弓高压端得到的功率减小。在输入雷击电流的瞬间,受电弓连接互感器线缆段出现功率波动,并且雷击电流越大,功率瞬间增长幅值越大,由于雷击电流变化速度过快,在0.03 ms 内无法完全衰减。这是由于雷击电流的输入会改变电缆电感,也会使得电弧形成的等离子体电容变化,从而增加电弧的电荷存储量和电弧电容对电压的敏感性。这会使得电弧的电压变得更加尖锐,从而改变受电弓侧高压端功率。
3.3 雷击电流对降弓电弧的影响
当对正常运行中的电弧施加一个很大的冲击电流,那么电弧的电压、电流和电阻会受到影响。本文仿真分析设置如下,在弓网系统产生降弓电弧过程中在时间2.013 ms 时输入雷击电流,得到稳定燃弧中的降弓电弧在施加不同倍雷电流后电弧电流、电压和电阻的变化情况如图13~15 所示。

图13 电弧电流对比图
在降弓电弧产生的瞬间,电弧的电阻会随时间的变化而变化,导致电弧的电压和电流在电弧产生的瞬间产生电弧波动。在2.00~2.013 ms 可以看出降弓电弧相比较一般燃弧出现滞后性,这是由于降弓过程中电弧弧柱拉长,弓网间自由电荷减少,空间中存在的自由电荷形成等离子体电容速度变缓,在受电弓极板与接触网之间充电时到达击穿电压的速度减慢。稳态燃烧的电弧电流也要小于弓网正常受流。降弓电弧遭遇雷击后,在0.057 ms 内电弧电流幅值随输入雷击电流的倍数逐渐增大,主要原因可能是雷电放电时弓网间隙导电开始吸引并加速周围自由电子和离子碰撞,形成电离雪崩的正反馈循环,造成雷击初始阶段电流振幅迅速增加。雷电向系统输入的短时强烈能量,电流振幅突然快速增加,导致等离子体通道中的电荷分离和电荷分布发生重大变化,从而导致电流振幅快速变化,在输入雷击电流的瞬间,电弧电流会出现剧烈电弧波动,并且雷击电流倍数越大,波动越剧烈。
分析不同雷击下降弓燃弧电压特性如图14 所示。

图14 电弧电压对比图
由图14 可知,降弓电弧电压的波形基本一致,也存在滞后性,相比于一般燃弧,降弓时峰值发生时间从2.007 ms 增长到2.008 4 ms。加入雷击电流并改变倍数对电弧电压的滞后性影响不大。在多次重燃中,雷击降弓电弧弧长持续拉长,过零后介质重击穿重燃的电弧电压也逐渐增大。2.028 ms 时电弧电压峰值为17.38 kV,2.068 ms 时电弧电压峰值达到21.81 kV。由图14 还可看出,由于电荷分离量和等离子体通道中的电荷量保持相对稳定,改变雷击倍数对电弧电压的增长影响不大,但在降弓电弧输入短时雷击电流后,输入雷击电流足够大时会出现剧烈反复的电弧波动,这是由于雷击过于强烈,导致电弧的温度过高,产生了非常强的电磁干扰,过电压幅值更大,高频暂态分量更丰富。
同时,对不同雷击下降弓燃弧电阻特性进行分析,如图15 所示。

图15 电弧电阻对比图
通过对比发现,降弓电弧相比于一般燃弧,电弧电阻会随着时间逐渐增大。雷击对于电弧电阻的增长影响不大,这是因为降弓运动会拉长电弧,导致电弧的电阻增大,而电弧电阻变化还要考虑形状、温度等因素,这些因素需要在较长时间内慢性地变化才能对电弧电阻有显著的影响,在短时间内输入电流也不会对电弧产生太大的热影响。当雷击发生时,等离子体通道中的电场增加,导致电子密度增加并形成燃烧电弧。这种电弧电流的增加伴随着电弧电阻的突然增加,随后由于更大的电弧通道打开,电弧电阻迅速减少。这种等离子体通道电阻突然增加和突然减少的反馈回路导致了电弧振荡,在输入雷击电流瞬间会出现电弧电阻突增,并以振荡形式快速衰减。
4 结论
为探究雷击下降弓过程对机车受流动态特性的影响,本文以传统电弧模型为基础,建立牵引系统环境下的弓网电弧综合模型,对比传统模型,确保了牵引系统电弧模型的准确性,从机车运行和电弧特性两个方面出发,探究了高压侧机车功率和整流侧电流的变化规律,同时分析了弓网电弧的动态特性。本文模型以73 km/h 的重载运行为研究对象,得到如下结论。
(1) 雷击降弓中的电弧使受电弓电源电压对电缆的寄生电容充电,由于机车高压端设备和受电弓的电感,影响了等效电路的振荡波动和过电压峰值。雷击能增强电场,改变电荷分离,并与高压端设备的电感和电容元件发生作用,影响机车高压设备端的供电情况。
(2) 雷击降弓电弧存在滞后性。在雷击过程中降弓电弧电流电压幅值随时间明显波动,基本呈现先增后减的趋势。改变雷击电流倍数可能会影响空气中带电粒子的浓度,间接影响等离子体通道的电阻。而由于热效应是长期过程,雷击电流时间短,在输入雷击电流的瞬间会产生剧烈的电弧波动,对电弧电阻改变较小。
(3) 输入的雷电电流会引起牵引系统电感电容变化,也会改变电弧形成的等离子体的电容,从而增加电弧的储电能力和电弧电容对电压的敏感性。
因此,雷击降弓电弧会导致过电压和功率的波动,这是一个复杂环境问题,需要采取更加全面的防雷措施保护机车以降低设备损坏风险。
