基于电容层析成像的电缆绝缘缺陷检测仿真研究*

2023-11-02林毅斌金雨潇钟理鹏孙秋芹

电气工程学报 2023年3期

林毅斌陈赦金雨潇钟理鹏孙秋芹汪沨

(湖南大学电气与信息工程学院长沙 410082)

1 引言

作为最主要的能源消耗和碳排放行业，交通的电气化改革和发展是实现我国“碳中和、碳达峰”目标的重要手段。电力电缆作为轨道交通系统的能源和信息的载体以及轨道电气化转型的重要设备，在交通领域起着举足轻重的作用，其绝缘状态直接影响轨道交通的稳定运行。然而，在复杂的运行环境和恶劣的运行工况下，电缆长期受到电、热、化学物质和机械外力等外部因素的作用[1]；同时，电缆在生产制造、运输储存和安装调试等环节中杂质的掺入和结构的缺陷不可避免[2-3]，在外部因素和电缆本体问题的共同作用下，电缆会出现气隙、水树等绝缘缺陷，造成绝缘性能下降甚至引发绝缘击穿，导致轨道系统停电，给交通运输带来巨大损失。

目前，电力电缆的绝缘检测方法可分为耐压试验、在线监测和介电特性检测三类。耐压试验存在无法完全反映电缆实际运行情况和检测具有破坏性等问题[4-5]，护层电流监测法、局部放电监测和分布式光纤测温等在线监测方法存在难以提取有效信号和局部缺陷不敏感等问题[6-7]，直流分量法和绝缘电阻法等介电特性检测存在检测过程复杂、检测信号微弱、难以识别局部缺陷等问题[8-10]，实际有效的电缆绝缘检测新技术亟待进一步的研究和探索。电容层析成像(Electrical capacitance tomography，ECT)技术是20 世纪80 年代提出的多相流在线检测技术，该技术利用电容传感器采集的被测区域电容值分布以及电容值与介电常数之间的关系，以二维或三维的形式图像化显示被测区域的介电常数分布[11-12]。ECT 技术具有成本低廉、检测速度快、灵敏度高、非侵入性和检测方式灵活等特点[13-14]，适合电缆集中性绝缘缺陷和分布性绝缘缺陷的在线监测，其在检测交联聚乙烯(Cross-linked polyethylene, XLPE)电缆含有大气隙绝缘缺陷的有效性已被初步验证[13]，但是XLPE 电缆含有微小气隙缺陷和其他典型缺陷的检测性能还有待进一步研究。

本文针对电缆绝缘缺陷检测的电容层析成像方法展开仿真研究。首先，针对XLPE 电缆和电容传感器搭建了电容层析成像模型，之后优化了灵敏场分布和电容传感器的几何参数，最后利用图像重建算法并结合优化后的灵敏场及电容传感器对四种典型的电力电缆绝缘缺陷进行了检测。

2 ECT 检测原理

2.1 ECT 系统结构和技术原理

一个完整的ECT 系统结构如图1 所示，主要由电容传感器、数据采集与处理单元和图像重建单元三部分组成[14]。

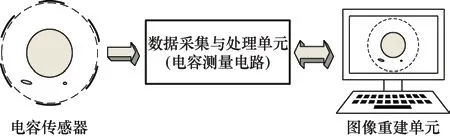
图1 ECT 系统结构

电容传感器用于采集被测对象和区域的电容信号，通常由电极、基底和屏蔽背板组成，传感器电极数量一般为偶数，典型数量为8、12 或16，每个电极可作为测量电极和感应电极，屏蔽背板与地相连屏蔽外部干扰，基底用于电极之间的绝缘。数据采集与处理单元，即电容测量电路，主要作用是测量电容传感器的电容信号并将其转换为与电容值成比例的电压信号，再处理成计算机可识别的数字信号，最后发送给图像重建单元。图像重建单元利用数据采集与处理单元传送的电容信息并选择合适的图像重建算法，重建被测区域的介电常数分布，并以二维或三维图像的形式显示。

ECT 的原理可分为正问题和逆问题两个过程，正问题是根据已知的电容传感器物理结构和测量区域内介质分布情况，通过数据采集与处理单元获取电容传感器的电容矩阵和被测量区域的灵敏度矩阵。逆问题是根据数据采集与处理单元获取的电容传感器所测量区域内介质的电容矩阵，选取合适的图像重建算法，利用正问题过程中求解的灵敏度矩阵重建被测量区域内介质的介电常数分布。

2.2 ECT 的数学模型

电容层析成像正问题的计算过程，即求解电容传感器测量范围内的介质分布情况和电容值的对应关系，其中的电磁场原理可以用麦克斯韦电磁方程组描述[15-16]

式中，H为磁场强度；J为电流密度；E为电场强度；B为磁感应强度；D为电位移；ρ为电流密度；σ为电导率；ε为介电常数；μ为磁导率。

由于电容层析成像系统是一个封闭的静电场，可以用泊松方程描述

式中，ε(x,y)为测量范围内介质的介电常数分布；φ(x,y)为测量范围内的电势分布，一般假设闭合的静电场中无自由电荷，即ρ=0。其边界条件有三种，其中电容层析成像的边界条件属于第一类边界条件，即狄利克雷(Dirichlet)边界条件

式中，S为场域边界；U为激励电极的电压。以8电极传感器的ECT 系统为例，测量过程中，当1 号电极作为激励时，其余7 个电极的激励电压应该为0 V 或接地。根据电容的定义，传感器电极之间的电容值Cij为

式中，Vij为加在激励电极i的电压幅值；Γi为围绕感应电极j的封闭曲面。

2.3 典型图像重建算法

ECT 逆问题主要是根据求解的灵敏度场和电缆电容值，利用图像重建算法计算电缆绝缘缺陷的分布[17]。ECT 图像重建算法主要分为直接算法和迭代算法两类，线性反投影算法(Linear back projection，LBP)和Landweber 迭代算法分别是直接算法和迭代算法中最常用的重建算法。

2.3.1 线性反投影算法

图像重建算法基本的求解公式为[18]

由于重建图像剖分单元的数量远大于测量的电容值数量，灵敏度场矩阵的逆矩阵S-1不存在，为此无法利用式(6)直接计算介电常数分布G。

为了解决这个问题，线性反投影算法采用灵敏度场矩阵的转置矩阵ST代替逆矩阵S-1的方法，实现介电常数分布的求解

LBP 算法将非线性问题直接线性化，具有求解过程简单和计算速度快的优势，但线性化过程中引入了较大误差，容易造成重建图像失真。

2.3.2 Landweber 迭代算法

Landweber 迭代算法根据最速梯度下降法，不断修正介电常数，从而提高重建图像质量[19]。

Landweber 迭代算法的最小化目标泛函为

待求函数f(G) 的梯度为

Landweber 迭代算法的计算公式为

式中，G0为LBP 算法计算的介电常数初始向量；Gk为第k步计算的介电常数向量；α为迭代步长；λmax为STS的最大特征值。

3 仿真模型构建与优化

3.1 模型构建

以某交联聚乙烯电力电缆为研究对象，利用COMSOL Multiphysics 完成八电极电容传感器和电缆二维仿真模型的搭建和电容值的计算，具体的仿真参数如表1 所示，仿真模型如图2 所示。

表1 电容传感器和电缆仿真参数

图2 电容传感器和电缆仿真模型

图3 所示电容传感器电极之间测量的电容值在180～676 fF，相邻电极与非相邻电极的电容值差值在3.8 倍，电容值呈对称分布。

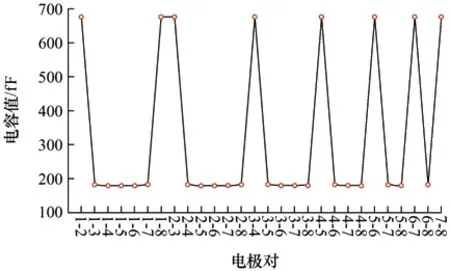
图3 电缆仿真电容值

3.2 电容传感器的仿真和设计

电容传感器的仿真和设计是研究XLPE 绝缘缺陷检测ECT 系统的重要环节，传感器的几何结构直接影响电容测量电路的设计，对ECT 系统的检测精度和成像质量有着显著影响，为此有必要进行电容传感器的仿真和优化。

电容传感器的几何结构如图4 所示，电容传感器由电极、基底和屏蔽层构成，此处基于提升传感器输出信号强度，同时减小电容传感器的动态范围的目标，研究电容传感器电极角度的优化。

图4 电容传感器几何结构图

利用建立的电容传感器和电缆仿真模型，修改传感器的电极角度，计算传感器电极角度与信号强度即电容值的关系，以及传感器电极角度与相邻电极电容值和非相邻电极电容值的比值，仿真结果图5 所示。非相邻电极如电极1 和电极3 之间的电容C13与电极角度是成正比的，相邻电极1 和电极2 之间的电容C12与电极角度的关系曲线是开口向上的抛物线，这说明传感器电极角度越大，电容值也越大，其中相邻电极的电容值对电极角度的变化更加敏感。

图5 传感器电极角度与电容值及比值的关系

对于ECT 系统而言，fF 级的电容是非常微小的，因此传感器电极输出的信号强度或电容值越大，有效电容信号越不容易被杂散电容淹没，电容测量难度也相对更小，增大传感器电极角度以获得更大的电容值是有利的。但是电极角度越大，相邻电极电容值和非相邻电极电容值之间的差距也愈发明显。

非相邻电极电容值和相邻电极电容值的比值越小，电容测量电路所需要测量的动态范围，即最小值和最大值差值也越大，这将增加电容测量电路的设计难度。同时在电极数量确定的情况下，电极角度越大相邻电极的间隙则越小，过小的间隙可能导致电极之间的放电，考虑到传感器电极的制作精度，为此不能无限制地增大电极角度，综合以上因素考虑，传感器的电极角度设计为40°，此时相邻电极的电容值达到了700 fF，非相邻电极与相邻电极电容的比值为0.27，电容测量电路的设计难度也更小。

3.3 灵敏度场求解与优化

灵敏度场描述了测量区域空间各点介质的介电常数加权值与电容值的关系。

空间各点权重反映了该点介电常数变化所引起电容值变化的大小，权重越大则说明该点对于介质介电常数的变化越敏感。传感器不同的电极对在测量区域同一点的权重也不相同，将所有电极对在空间各点的权重组合起来便得到了“灵敏度场”。

ECT 灵敏度场的计算公式为[20]

式中，Cij为传感器电极i和电极j之间的电容值；S[(x,y),ε(x,y)]为点(x,y)的介电常数是ε(x,y)时，传感器电极i和电极j之间的灵敏度。

根据式(13)可知，灵敏度不仅与介质的空间位置有关，还与介质本身的介电常数有关，这被称为ECT 的“软场特性”。为了简化运算，一般忽略介质本身介电常数的影响，将式(13)局部线性化和离散化，简化的灵敏度场模型为

式中，C是m×1 的电容值向量；S是m×n的灵敏度矩阵；G是n×1 的介电常数分布向量；m为传感器电极组成的互电容个数；n为测量区域内介质被剖分的网格数。

灵敏度场的定义式为

式中，S ij(k)为电极i和电极j组成的灵敏度场中第k个点的灵敏度；hε和lε分别是介质的高介电常数和低介电常数；Ci j(k)是除了测量区域第k个点的介电常数为高介电常数，其他区域都为低介电常数时，电极i和电极j之间的电容值；和分别是测量区域内的介质都为高介电常数和低介电常数时，电极i和电极j之间的电容值；μ(k)是测量区域第k个点的面积补偿因子。

电势法在确定激励电极和感应电极后，COMSOL 运行一次则可计算对应电极对下所有网格的灵敏度场，为此COMSOL 只需要运行m次即可，此方法极大地减少了COMSOL 的运行次数，节约了整体计算时间。特别是在网格细密和单元数量较多的情况下，电势法计算速度的优势更加明显，电势法的灵敏度场计算如式(16)所示

式中，E i(x,y)为电极i作为激励电极且电压值为Vi时测量点(x,y)的电场强度；同理E j(x,y)为电极j作为激励电极且电压值为Vj时测量点(x,y) 的电场强度；p(x,y) 为点(x,y) 的面积。

根据电势法公式，利用COMSOL with Matlab接口，联合Matlab 和COMSOL 共同求解灵敏度场。电势法直接求解的灵敏度场如图6 所示。

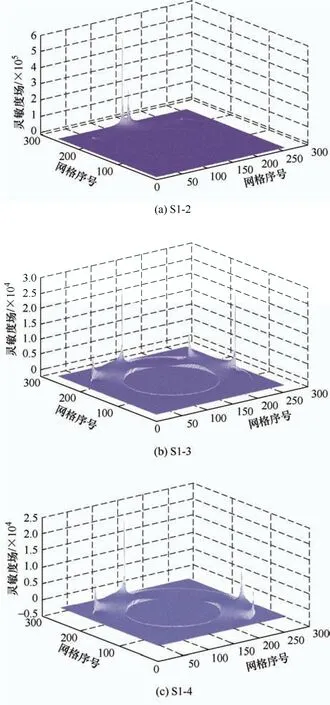
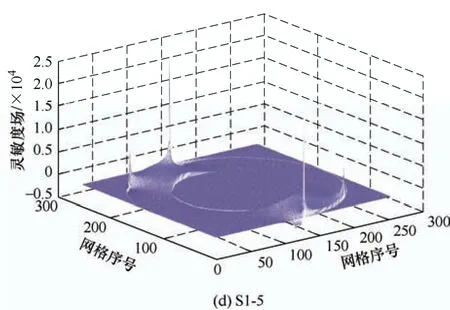
图6 电势法求解的部分灵敏度场

其中，电极两端的电场变化很大，该位置的灵敏度值是其他区域的数十倍，太大的灵敏度值将产生噪点严重影响后期的成像效果，为此需要优化灵敏度场分布。中值滤波是一种基于排序统计理论的非线性信号处理方法，在消除图像的随机噪声上具有优异的效果，特别是脉冲干扰[21-22]。

采用中值滤波算法，以滤波单元输出的灵敏度中值代替原单元的灵敏度，得到优化后的灵敏度场如图7 所示。

由图7 可见，电极两侧的尖峰已经被消除，有效地提高了灵敏度场的均匀性，模型整体的灵敏度场分布趋势保持不变，电极区域的灵敏度场由中间向两侧的过渡更加平滑自然，为后续图像重建工作打下了坚实的基础。

4 XLPE 电缆绝缘缺陷仿真检测

XLPE 电缆绝缘缺陷仿真设计了绝缘层的气隙缺陷、水树缺陷、楔形划痕缺陷和复合缺陷共4 种典型缺陷，采用Landweber 迭代算法重构电缆内部绝缘缺陷的分布图像并分析成像质量。

水树缺陷模型中，水树采用椭球结构模拟水树真实的介电常数变化[23]，如图8 的水树缺陷模型示意图所示。椭球结构是由一系列充水微孔和树枝通道交替链接组成的，其中充水微孔是长半轴为5 μm，短半轴为3 μm 的不完整椭圆，相对介电常数为81，树枝通道是宽度为3 μm，长度为10 μm的矩形，相对介电常数为4.6，模型中的水树为内导型水树，起始于导体和绝缘层的交界处向护套层延伸，长度为2 mm。

图8 水树缺陷示意图

单气隙绝缘缺陷模型模拟XLPE 电力电缆绝缘层出现气隙缺陷的情况，模型中绝缘层的相对介电常数为2.5，气隙的相对介电常数为1，气隙半径设置为0.5 mm，单气隙缺陷仿真模型如图9 所示。

图9 单气隙缺陷几何图

楔形划痕缺陷容易出现在电缆接头制作时，施工装配过程中的物理外力作用致使XLPE 表面出现破损划痕，仿真模型中的楔形划痕设置在XLPE 电力电缆的绝缘层中，其截面为一个边长为1.5 mm 的等边三角形，划痕区域的相对介电常数设为1，楔形划痕缺陷仿真模型如图10 所示。

图10 楔形划痕缺陷几何图

在恶劣环境下长期使用的电力电缆难免会存在多处局部缺陷，为检验ECT 对复杂情况下的局部缺陷的测量效果，开展复合缺陷的仿真很有必要。为此，在电缆绝缘层的两个不同位置分别设置了一个楔形划痕和半径为0.5 mm 的圆气隙作为复合缺陷，用于模拟XLPE 电力电缆绝缘层存在多处绝缘缺陷的场景，复合缺陷仿真模型如图11 所示。

图11 复合缺陷几何图

通过COMSOL 计算各缺陷的电容值分布，将电容值矩阵和优化后的灵敏度场导入至Landweber迭代算法中，对气隙缺陷、水树缺陷、楔形划痕缺陷和复合缺陷分别进行图像重建，缺陷的几何结构和重建结果如图12 所示，其中横坐标和纵坐标为检测区域所剖分的单元格序号，图例为相对介电常数的变化值。

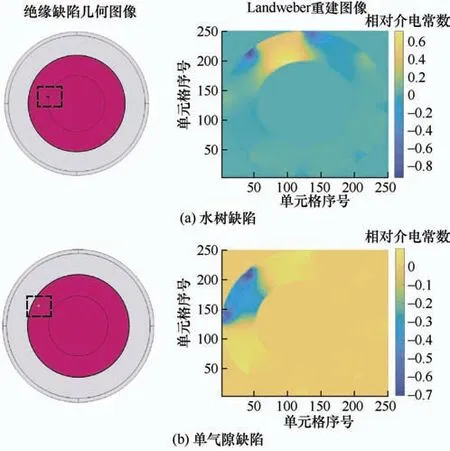
图12 四种典型绝缘缺陷的图像重建结果

由图12 可知，Landweber 算法能够重建出突出的缺陷特征，不同深浅代表相对介电常数的变化，以此来判断绝缘缺陷的有无和大致位置。在黑白灰图像中，灰色的深浅对应相对介电常数的高低，其中，气隙缺陷和楔形划痕缺陷附近相对介电常数下降，如图12b～12d 中深色区域所示；水树缺陷附近相对介电常数升高，如图12a 中浅色区域所示，该特点区别于气隙缺陷和楔形划痕缺陷。图像重建结果表明，该仿真设计能够实现对气隙缺陷、楔形划痕缺陷、水树缺陷和复合缺陷的检测，特别是可以检测并分辨出水树这一绝缘缺陷类型。