一种迫击炮内弹道模型与仿真

王戴思源，张领科

(南京理工大学 能源与动力工程学院，江苏 南京 210094)

迫击炮武器是一种伴随和支援步兵作战的有效压制武器,具有质量轻、体积小、机动性好等优点[1],作战任务包括近距离杀伤敌有生力量与摧毁轻型工事或桥梁建筑以及丛林反恐等,在城市战、登陆战等作战场景中有着重要作用。迫击炮武器因其有着不同于一般武器的装药结构和发射方式而具有特殊的内弹道过程。迫击炮经典内弹道模型将迫击炮弹尾管内基本装药的燃烧过程进行了简化,认为其属于定容燃烧,然而,尾管在破孔之后实际上会同弹后空间组成一高低压室,并发生燃气和火药颗粒的交换,因此有必要针对该过程建立模型并重构迫击炮零维内弹道模型。

国内外许多学者对迫击炮武器的内弹道模型进行了研究,赵雨馨等[2]构建了弹炮间隙的气体流出量模型,并结合迫击炮经典内弹道模型对迫榴炮武器发射迫弹的内弹道过程进行了仿真计算。陆林等[3]将液体发射药技术应用于迫击炮发射过程中,建立了液体发射药迫击炮内弹道模型。杨博伦等[4]针对液体发射药火炮在低膛压发射情况下的特点,建立了再生式液体发射药迫击炮内弹道模型。白昌盛等[5]和张楠[6]基于迫击炮经典内弹道模型,通过构建变燃速发射药的几何燃烧模型,对迫击炮变燃速装药情况下的内弹道性能进行了仿真计算。

以上研究基于的迫击炮经典内弹道模型认为,当传火孔打开后,基本装药瞬间全部进入主药室与辅助装药一起燃烧,且尾管压力与主药室内的压力保持一致,初始压力根据破孔时的基本装药燃烧情况得到。对此,Anderson[7]认为尾管与弹后空间实际上形成了一种高低压室,且高低压室内部存在气体与基本装药颗粒的交换,其基于IBHVG2[8]模型构建了迫击炮高低压室(HILO)模型,并对迫击炮的内弹道过程进行了仿真分析。Schmidt等[9]在此模型基础上进一步完成了迫击炮装药和迫弹等参数的敏感性分析。

笔者在HILO模型的基础上考虑了燃气温度对流量的影响从而修改了气体流量方程,并且由于迫击炮发射药一般为弧厚较薄的片状药,因此替换了颗粒流量方程以适用任意药型的基本装药,结合国内迫击炮经典内弹道模型,推导了能量方程与状态方程,构建了一种迫击炮零维内弹道模型,针对某120 mm迫击炮结构和全装药进行了数值计算和结果分析,可为迫击炮的内弹道仿真提供参考。

1 物理模型

某120 mm迫击炮内弹道过程示意图如图1所示,可以将其大致分为两个阶段。

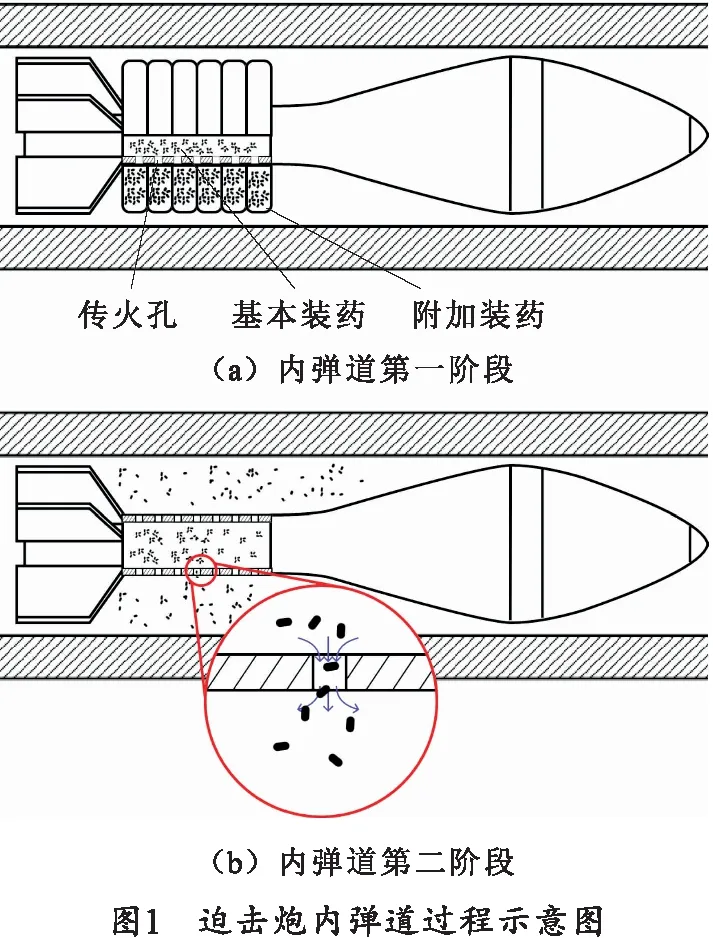
第一阶段:受重力影响,迫击炮上基本药管内的底火与身管上击针撞击而发火,首先点燃点火药,继而点燃基本药管内的基本装药,由于传火孔被封闭,基本装药处于定容燃烧阶段,迅速产生高温高压的火药燃气。

第二阶段:当燃气压力达到衬纸所能承受的最大压力后,火药燃气突破衬纸通过传火孔而逸出至弹后空间[10],此时基本装药尚未燃烧完全,会随着火药燃气的逸出而进入主药室继续燃烧,而基本药管与弹丸后部自由空间就构成了一个典型的高低压室,当高低压室的压力不平衡时,会发生火药燃气的质量交换。随后,燃气点燃固定在尾管上的附加装药进一步释放火药燃气,从而推动弹丸继续向前运动。此外,由于迫弹与身管存在间隙,主药室内的火药燃气会部分的泄漏至外部环境。

根据上述迫击炮特殊的装药结构与内弹道过程,建立迫击炮内弹道数学模型,并作出如下基本假设:

1) 尾管未破孔前,基本装药在尾管内定容燃烧,打开传火孔后,燃气从尾管中流出并点燃附加装药。

2) 传火孔打开后,燃气能在尾管和弹后空间交换,并携带着基本装药颗粒一同运动。

3) 基本装药颗粒在点火药管内分布均匀且逸出尾管后不再倒流。

4) 火药燃烧符合几何燃烧定律。

5) 火药燃气通过传火孔或身管与弹丸间隙时,满足的状态条件取决于两侧压力。

6) 热损失不作直接计算,通过减小火药力的方法,间接修正热损失的影响。

2 数学模型

基于以上假设,建立了具有高低压室的迫击炮零维内弹道方程组。

2.1 高低压室模型

气体流量方程为

(1)

(2)

式中:g为重力加速度(m/s2)。

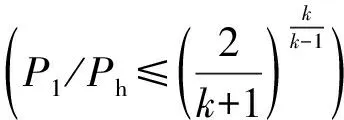
(3)

式中:Ph和P1分别为高压药室和低压药室内的燃气压力(MPa)。

颗粒流量方程为

(4)

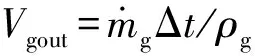
(5)

式中:ω0为基本装药的装药量(kg);ωsingle为单个基本装药的质量(kg);e′1、b′、c′分别为火药颗粒的1/2弧厚、宽度和长度(m);ρp为基本装药的火药密度(kg/m3)。

基于诺贝尔-阿贝尔方程推导尾管状态方程,尾管内的火药燃气压力变化情况复杂,首先基本装药先在尾管内定容燃烧,此时仅需考虑火药颗粒体积和余容即可计算尾管自由容积,但当传火孔打开后,一方面有燃气从尾管内流出或从主药室流入,另一方面又有火药颗粒的流失所导致的膛内火药颗粒数量减少,尾管自由容积需要特别计算,这里引入了ωc来表示火药颗粒泄露前已经燃烧释放的火药燃气质量。尾管内燃气压力pwg计算方程为

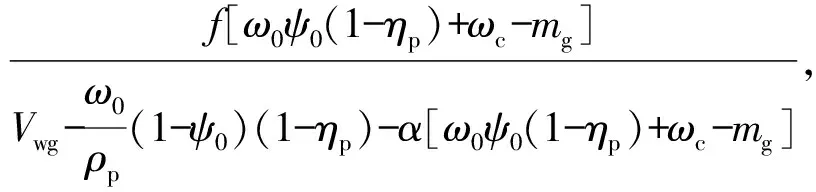
(6)

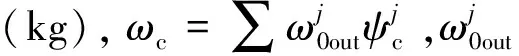
2.2 迫击炮内弹道基本方程

因迫击炮装药通常采用燃速较大的薄火药,此处仅考虑片状药型的形状函数:

(7)

式中:αi为主药室内各种火药的质量分数;χi、λi、μi为火药形状特征量;Zi为第i种火药的已燃厚度(m)。

火药燃速方程为

(8)

式中:u1为火药燃速系数(m/(Pan·s));n为火药燃速指数;p为主药室内的燃气压力(Pa)。

弹丸运动方程为

(9)

式中:v为弹丸速度(m/s);S为迫弹定心部横截面积(m2);φ为次要功系数;m为弹丸质量(kg)。

弹丸速度与行程关系式为

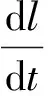
(10)

式中,l为弹丸行程(m)。

间隙流量方程为

(11)

式中:η为主药室内的燃气从弹丸与身管间隙流出的相对质量;φj为燃气从间隙流出的燃气泄漏系数;Sj为迫击炮定心部与身管的间隙面积(m2);ω1为附加装药的装药量(kg)。

由于迫击炮在膛内的运动过程中存在着高低压室和与外界的气体质量交换,其中还有基本装药的泄露,因此其主药室内的能量变化情况十分复杂,有必要针对性的构建其能量守恒方程。膛内的能量变化主要有以下5个方面:

(12)

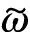
2)推动弹丸所做功:

dE2=φmvdv.

(13)

3)从主药室流出的燃气带走的能量:

(14)

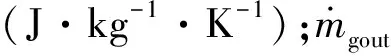
4)流入主药室的燃气带来的能量:

(15)

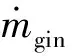
5)留在膛内的能量:

(16)

根据能量守恒定律,有

dE5=dE1-dE2-dE3+dE4.

(17)

化简得

(18)

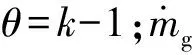
气体状态方程为

(19)

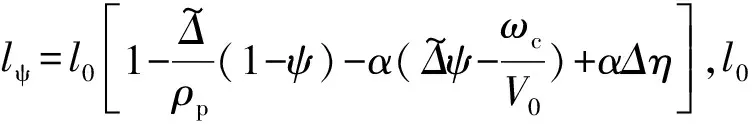
3 仿真结果与分析

针对某120 mm迫击炮内弹道过程进行仿真计算,求解方法使用4阶Runge-Kutta法,不考虑点火药,破孔压力为95 MPa,基本装药采用35-2×100药,附加装药采用4/1药,部分装药和输入参数如表1所示。

表1 仿真参数表

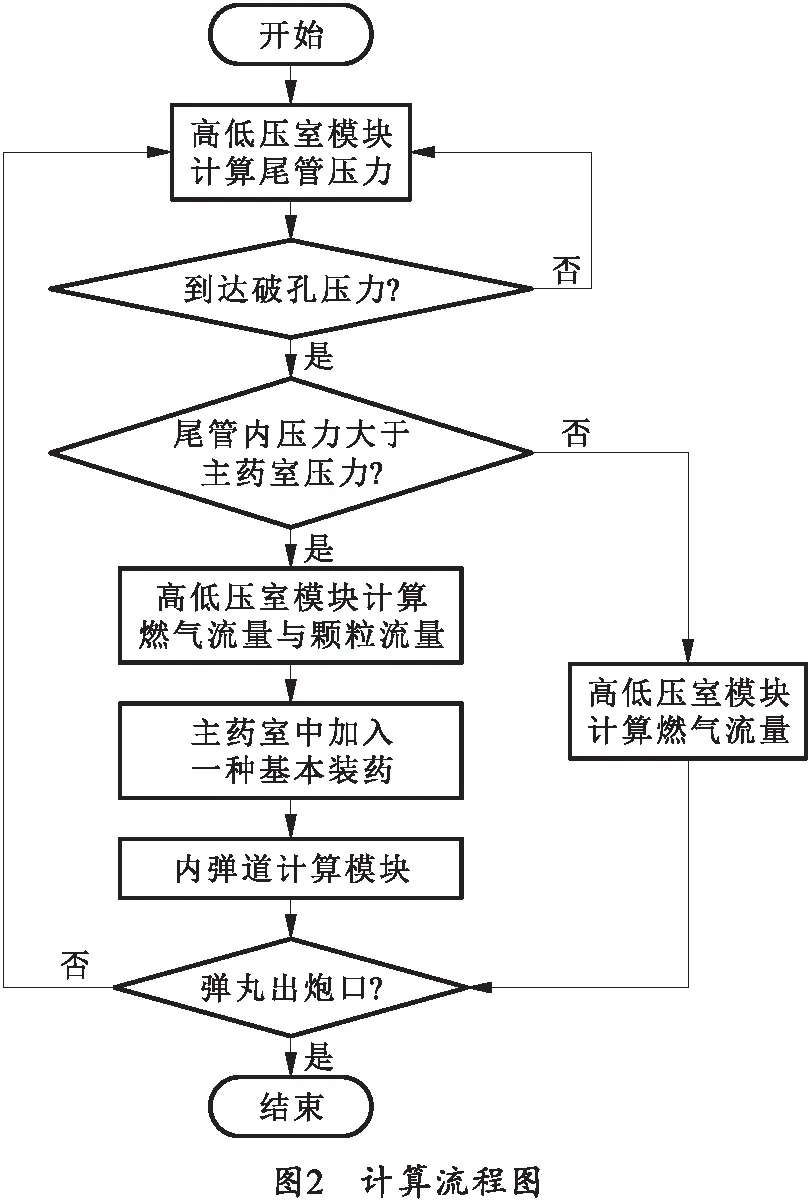
使用C++语言编写模型求解程序,程序计算流程图如图2所示。首先调用高低压室模块计算尾管压力并判断破孔条件,接着计算两室之间的气体交换流量,再根据气体流量计算具体的基本装药泄露情况,在已知高低压室模块的计算结果后,使用内弹道主模块计算具体的膛内压力、弹丸速度和加速度等参数,程序将循环计算直至弹丸出炮口。

此外,在计算中还需要对基本药管内的颗粒流出至主药室这一过程进行特别的程序设计,具体做法:计算中的每一时间步的颗粒流出质量计算完成后,程序将在主药室添加相应装药质量的一种火药,此火药除装药质量外的其余属性均与基本装药相等,下一时间步该火药则基于弹后平均压力进行燃烧。

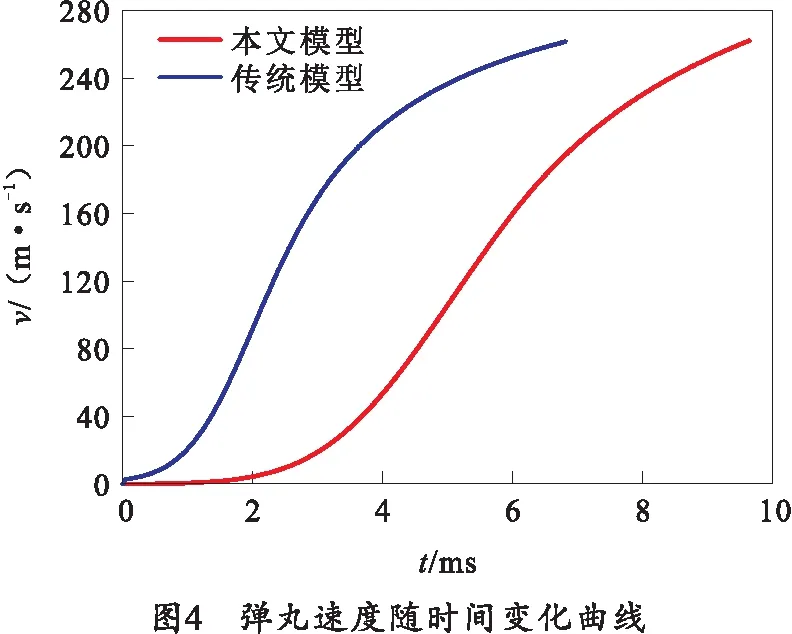
为验证模型能正确反映迫击炮内弹道过程,采用上述计算程序仿真得到某120 mm迫击炮内弹道参数,并与不考虑高低压室的传统迫击炮模型计算结果以及试验值进行对比,三者的弹丸初速与最大膛压列于表2中。

表2 仿真结果比较

与试验值相比,仿真计算的最大膛压误差值为0.04%,炮口初速的计算误差值为0.02%,因此,本文模型计算所得结果与试验值具有较好的一致性,能够较好地反映迫击炮内弹道过程。

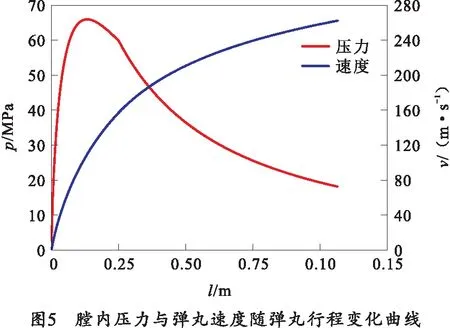
为了说明笔者建立的模型所反映的迫击炮内弹道过程与传统模型在反映迫击炮内弹道过程中的差异,将仿真结果与传统迫击炮模型计算所得内弹道参数变化规律曲线进行比较,绘制出内弹道过程曲线如图3～5所示。

从图3可以看出,在内弹道过程的初期,基本装药在尾管内首先进行定容燃烧,燃烧释放的火药燃气迅速充满整个尾管并且压力不断上升,压力达到破孔压力95 MPa后,与传统不考虑高低压室的迫击炮零维内弹道模型不同的是,尾管向弹后空间开始泄漏基本装药燃气,反映了附加装药的点火过程,进而引起膛内压力的不断上升,因此,笔者所建立模型较传统模型存在明显的膛内压力上升过程滞后。此外,在尾管压力与膛内压力一致后,尾管与膛内无较大的压力梯度,在图中反映为尾管压力曲线与膛内压力曲线基本重合。

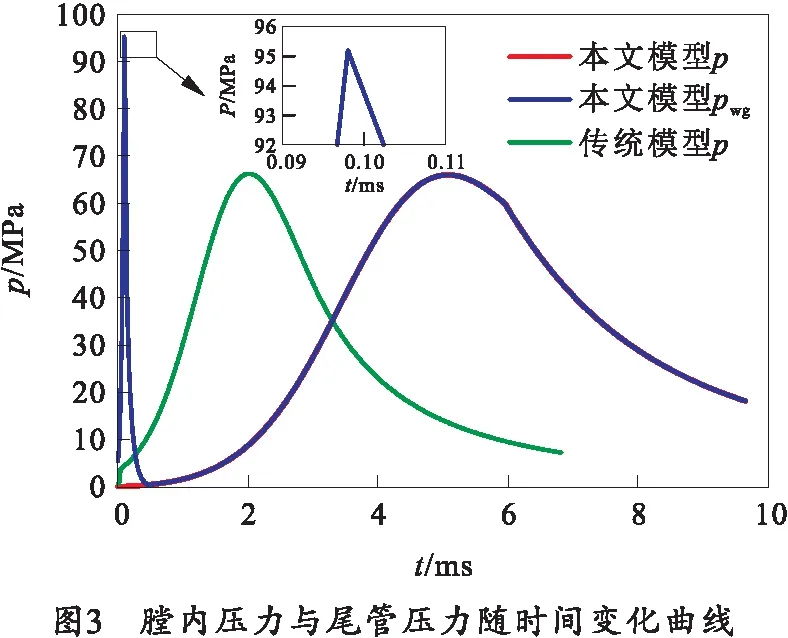
随着燃气从尾管流出,基本药管内的火药颗粒进入弹后空间导致尾管压力迅速下降,图6展示了基本药管内火药颗粒的泄漏情况。

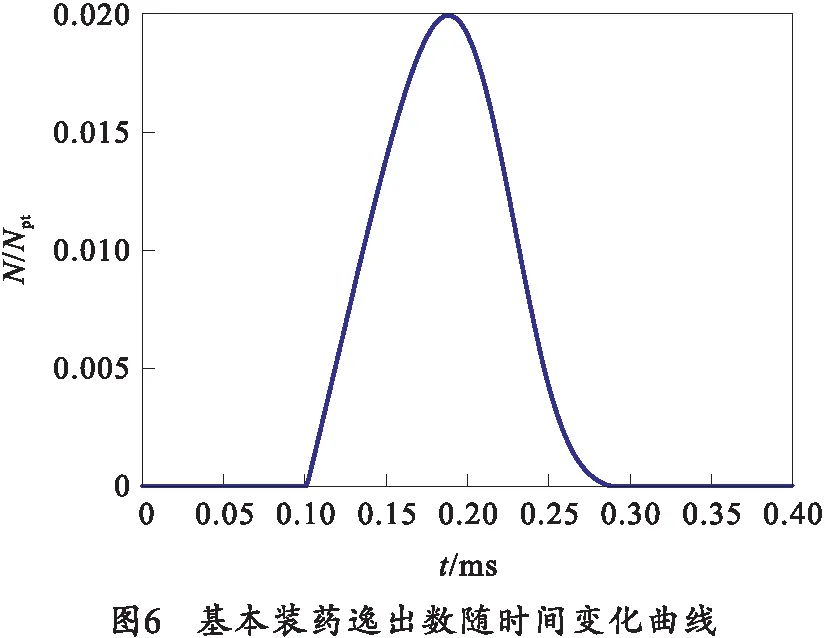
当基本火药燃气引燃的附加装药开始燃烧,其与泄漏至弹后空间内的基本装药一起释放火药燃气,又由图3可以看到,在0.63 ms处弹后空间燃气压力开始大于尾管内燃气压力,燃气开始回流至基本药管内,根据之前的基本假设:燃气向基本药管回流时不会携带弹后空间内的火药颗粒倒流,因此从图6可以看出,在0.3 ms后逸出的颗粒数量为0。当基本药管内的颗粒完全流出后,尾管实际上成为了一个迫击炮尾部携带的气缸,尾管压力会随着主药室的压力而变化。

图7展示了弹丸膛内加速度随时间的变化规律。从图7中可以看出,整个弹丸膛内加速度变化趋势与膛内压力变化一致,加速度峰值出现在最大膛压时刻,最大值为55 766 m·s-2。

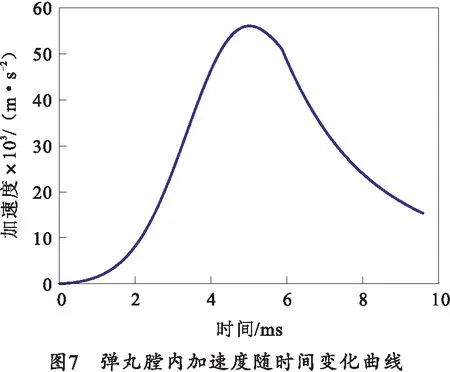
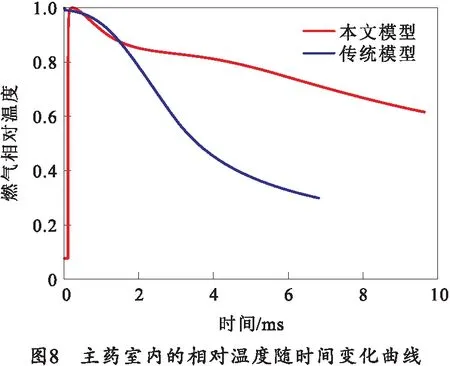
图8展示了迫击炮内弹道过程中的主药室燃气相对温度随时间的变化曲线,与传统模型的不同在于,主药室内的燃气温度在高低压室发生燃气交换之前保持常温,随后由于尾管内燃气的输入和主药室内基本装药与附加装药的燃烧释放火药燃气而导致了其中的火药燃气温度有明显的上升至爆温的过程,接着又因为燃气推动弹丸做功,且对外部环境和尾管存在燃气的流失,能量不断损失,所以燃气压力随时间逐渐下降。

4 结束语

为了精确描述迫弹尾管与主药室之间的燃气交换导致的附加装药点火过程,针对迫击炮特殊的装药结构和内弹道过程,在HILO模型的基础上修改了气体流量方程与颗粒流量方程,构建了尾管压力方程,并结合迫击炮经典内弹道模型,推导了能量守恒方程与气体状态方程,建立了一种考虑高低压室的迫击炮零维内弹道数学模型。

针对某120 mm迫击炮结构及全装药进行了数值计算,得到了迫击炮尾管压力、膛内压力、弹丸速度和加速度的变化规律,分析了高低压区间的基本装药流量和主药室内的能量变化过程,并将仿真结果与试验数据进行了比较,得到膛内压力误差为0.04%,弹丸初速误差为0.02%,表明了仿真值与试验值具有很好的一致性,验证了模型的正确性。结果表明模型能够较好地反映迫击炮的实际内弹道全过程。