基于刚柔耦合动力学模型的某协调输弹机机构可靠性分析

苍竹，徐亚栋，鲁飞，羊柳，刘太素

(1.南京理工大学 机械工程学院，江苏 南京 210000；2.中国人民解放军32381部队，北京 100072)

弹药自动装填系统是火炮武器系统的重要组成部分,其发展提高了火炮武器系统的射击速度,增加了火炮武器威力[1]。协调输弹机是自动装填系统的重要组成部分,用于将接收的弹丸由取弹位协调至输弹位,并将弹丸输送到炮膛内。输弹到位时弹丸的卡膛状态对火炮射击精度有重要影响。通常,弹丸卡膛状态由弹丸卡膛速度和弹丸姿态表征。在加工生产中,协调输弹机构的尺寸、安装位置等参数存在不确定性,导致弹丸卡膛状态不一致。因此,开展协调输弹机可靠性分析,对工程实际中提升弹药自动装填系统可靠性具有指导作用。

现有研究拆分协调输弹两结构对单系统进行分析,已取得丰富研究成果。文献[2]基于区间参数的不确定性分析方法建立输弹机动力学模型,分析输弹参数不确定性带来输弹动力学响应的变化。文献[3]建立面向输弹一致性的输弹机稳健优化模型,采用全局和梯度组合优化算法以及描述抽样,提高输弹一致性。文献[4]提出基于概率密度演化理论的输弹过程不确定性分析方法,分析火炮输弹过程不确定性参数对输弹一致性的影响。文献[5]在协调器协调65°的工况下,针对某弹协调器的定位可靠性进行仿真分析及可靠度计算。文献[6]对弹药协调器进行了不确定性建模,构建了基于径向基神经网络的代理模型拟合原始模型进而仿真分析弹药协调器的动作可靠性。文献[7]采用基于Kriging和蒙特卡洛的方法对协调器进行姿态可靠度计算。文献[8]利用蒙特卡洛模拟方法考虑关键的随机性进行某火炮自动装填系统协调器动作功能及结构强度可靠性分析。

完整的弹药装填流程是由一系列互相衔接动作组成的,任一动作的异常都会影响下一动作的进行[6]。弹丸装填经历协调过程与输弹过程,协调阶段协调姿态误差超出精度指标可能不会导致协调动作彻底失败,但这种影响会在输弹过程中体现,可能由于弹轴偏离炮膛轴线而产生额外的接触碰撞,降低卡膛速度,改变弹丸姿态最终导致弹丸装填失败。故进行机构可靠性研究时也要考虑协调阶段的不确定性对弹丸卡膛的影响。

可靠性即在规定时间内和规定条件下结构机构完成规定功能的能力[9]。经典的可靠性分析方法采用概率理论对不确定因素进行描述,继而通过不确定性传递分析量化相应量的不确定性,得到结构机构的可靠度(或失效概率)[10]。

笔者从原理上分析了协调输弹机的协调、输弹过程,考虑协调输弹机机构制造安装及弹丸物理参数随机性,利用ADAMS建立刚柔耦合协调输弹机动力学模型。由此建立协调输弹机机构可靠性功能函数,结合蒙特卡洛法进行可靠度及灵敏度计算,对协调输弹机进行可靠性分析。

1 刚柔耦合动力学分析

1.1 调输弹机机构形式及运动原理

协调输弹机由协调电机、输弹电机、协调机构、输弹机构组成。协调机构由协调齿弧及协调臂、协调限位块组成,结构简图如图1所示。协调输弹机在协调电机作用下由接弹位运动到输弹位,协调臂上的协调齿弧与驱动齿轮啮合,使得协调臂绕耳轴旋转,令弹丸轴线与身管轴线平齐,完成协调动作。

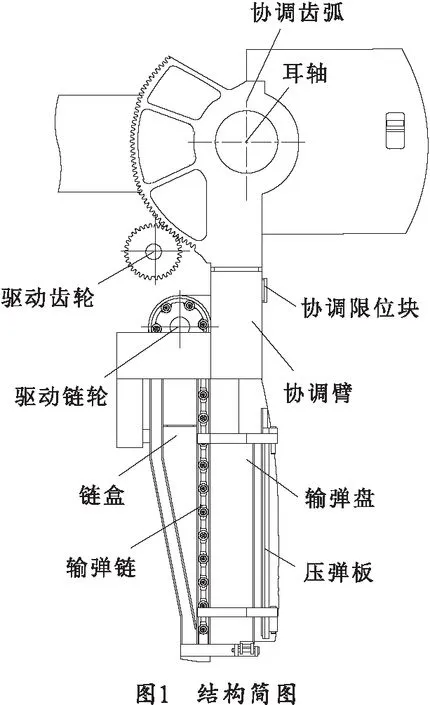
输弹机构由输弹盘、压弹板、链盒、输弹链构成。输弹盘及压弹板用以限制弹丸自由度。输弹机构通过压弹板确保运动过程中的压弹可靠。输弹链为开式链,链轮驱动输弹链由链头推动弹丸前进完成输弹动作。

1.2 建模描述假设

为便于相对准确建立协调输弹机刚柔耦合动力学模型,分析协调输弹过程,对该模型进行如下假设:

1)炮身与大地固连,忽略炮身振动与变形。

2)协调输弹过程中协调输弹机与弹丸的运动均为二自由度的平面运动。

3)弹丸是否卡膛到位以弹底到卡膛点的距离来判定,当距离达到一定值后,卡膛到位。

4)弹丸与炮膛间的碰撞为弹性碰撞,简化为弹簧阻尼模型。

5)考虑弹丸与炮膛间的摩擦,摩擦系数为定值。

6)不考虑摩擦热在输弹过程中的影响。

协调输弹机刚体动力学模型拓扑结构如图2所示,运动副形式与接触关系在图2中标出。

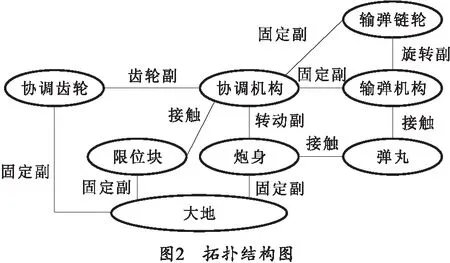
协调臂本质上属于悬臂梁结构,协调过程中要求其在短时间内完成大幅度转动,协调臂的弹性变形不应被忽略。此外协调臂的弹性变形会直接影响输弹状态,故有必要对协调臂进行柔性化处理,协调臂柔性模型如图3所示。以此替换原来的弹协调臂刚体并对刚柔耦合模型再次进行计算。

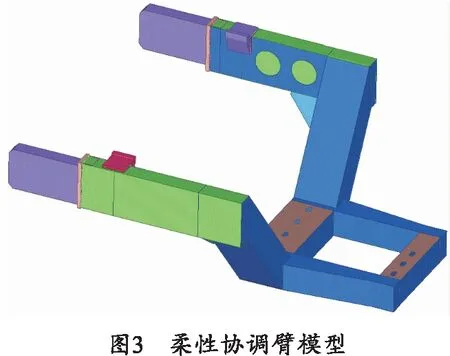
1.3 模型驱动

笔者以在0°射角工况下应用输弹试验采集所得协调齿轮与输弹链轮的角速度作为模型驱动,考虑协调到位和输弹入膛两个阶段,不考虑输弹回链与协调臂归位阶段角速度,得到协调齿轮驱动角速度曲线和输弹链轮驱动角速度曲线,分别如图4、5所示。

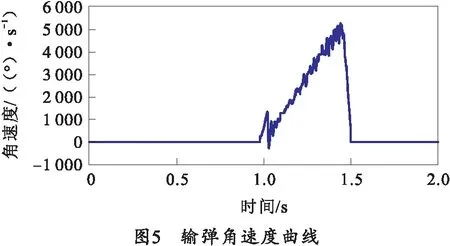
1.4 模型仿真结果分析

在动力学仿真模型中创建位置传感器,令弹丸到达卡膛位置前2 mm仿真终止,并将此时刻的弹丸速度认为是卡膛速度。同时创建弹丸轴线与炮膛轴线在垂直于地面方向上的角度测量,仿真终止时刻的测量角度即为文章所指弹丸姿态角,对上述模型进行仿真计算。确定模型的各响应随时间变化如图6～9所示。

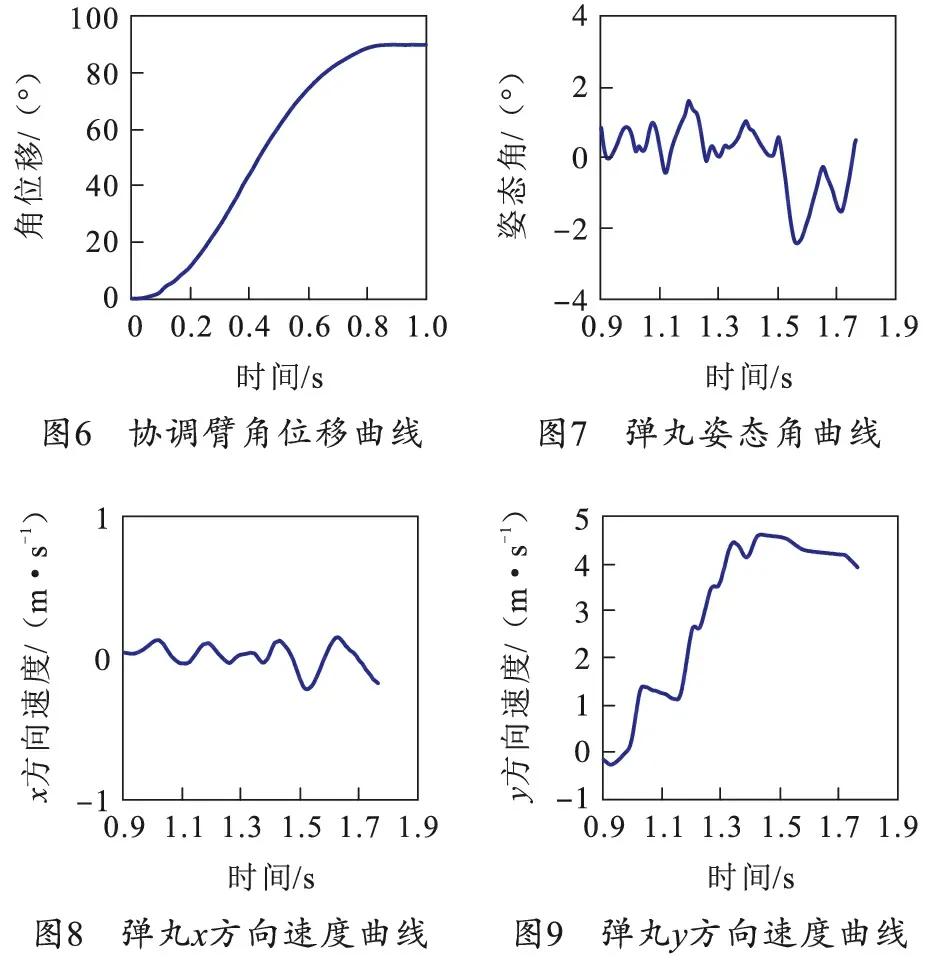
从图6～9中可以看出,0—0.9 s为协调阶段,协调臂在协调过程中先变加速到中间位置再变减速到达输弹位置,由于到位后协调臂与限位块发生接触碰撞,协调臂角度产生细小振荡;0.9 s后为输弹阶段,图中y方向为弹丸前进方向,弹丸在输弹过程中经过两次加速后达到峰值,1.5 s后进入惯性输弹阶段,弹丸在膛内与炮膛内壁发生摩擦与碰撞,速度逐渐减小,最终在1.78 s卡膛完成。由于输弹驱动的角加速度非定值,导致弹丸速度与弹丸姿态角呈现波动状态。仿真结果与真实情况基本一致。

2 机构可靠性建模

2.1 输入变量

考虑由于设计制造装配误差及环境因素带来的影响,导致协调输弹机输弹盘长度、输弹盘内径、输弹盘焊接位置、链轮基圆半径、滚轮半径、滚轮间距、输弹机定位偏差在设计值附近随机波动;同时考虑弹丸的加工误差与装药量偏差引发的弹丸质量、质心位置等参数的随机性对运动功能的影响,因此,笔者将上述参数选取为随机变量。

假定随机变量相互独立且服从正态分布。结合工程实例为各随机变量选定统计特性数据,如表1所示,其中序号1～10为可进行修改与优化的变量,序号11～13为作为考虑弹丸影响的变量。表中序号4～7与11～13中所提均基于全局坐标系,xy平面与地面平行,xz平面与地面法向垂直。

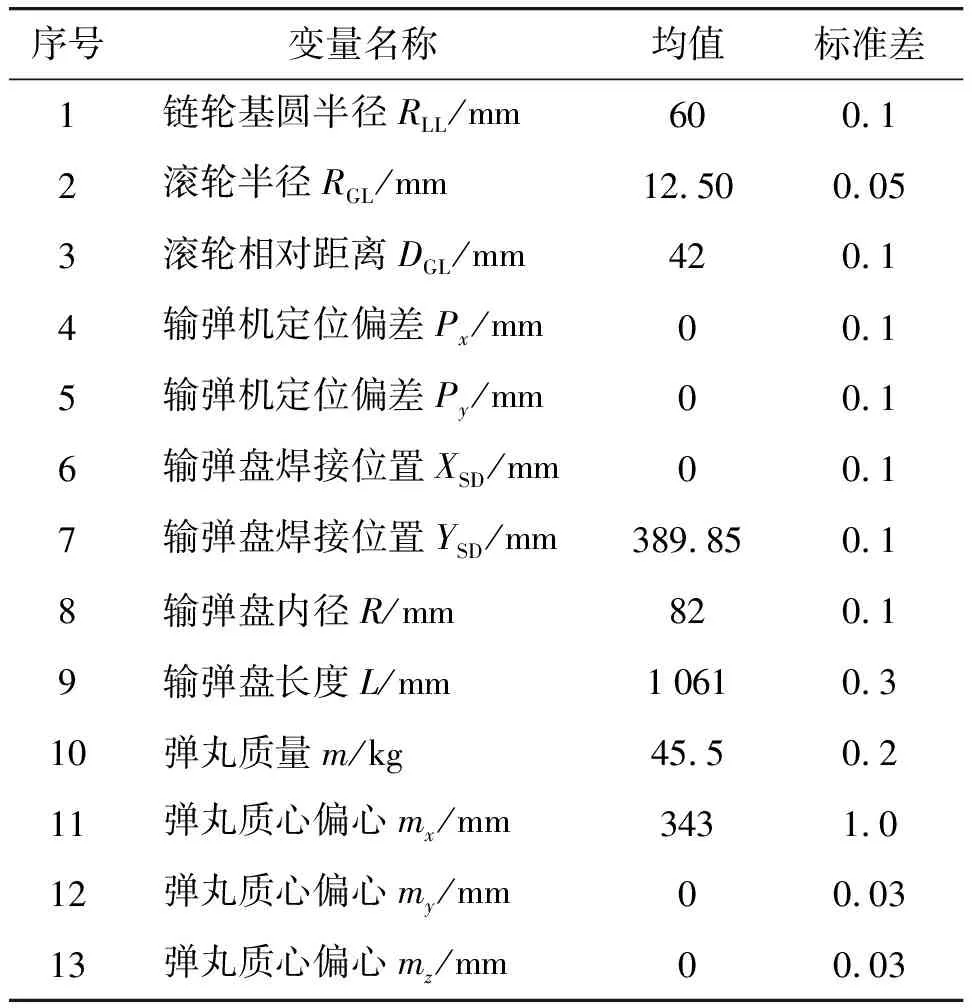
表1 随机输入变量

2.2 机构失效判据

弹丸卡膛结果是弹丸装填重要参数,决定了弹丸膛内运动最起始状态,不同的卡膛结果会导致整个膛内运动过程的不一致[11]。协调输弹机的机构失效最终体现在弹丸卡膛状态上(包括弹丸卡膛速度和弹丸姿态)。

协调输弹机要保证卡膛速度不小于预定值时弹丸姿态角在合理范围内。因此,在评估协调输弹机机构可靠性时,应先进行卡膛速度判断,在卡膛速度达到要求时判断弹丸姿态角是否达到预期效果。

弹丸卡膛速度是弹丸装填的重要参数,对火炮射击精度会产生无法忽视的影响,其数值不能低于预定值V*,卡膛速度的功能函数为

g=V(x1,x2,…)-V*,

(1)

式中:g>0即为满足卡膛速度要求;V为实际卡膛速度;x1,x2,…,为影响卡膛速度的随机变量;V*为理想卡膛速度,根据要求设置为3 m/s。

弹丸的姿态是火炮射击密集度的重要影响因素[12]。弹丸卡膛姿态角指的是卡膛过程中弹丸轴线与身管轴线夹角的变化。弹丸姿态偏差是产生炮口初始扰动的主要原因[13],直接影响火炮的射击密集度。实际姿态角与理想姿态角的差值不能高于预定值ΔA,弹丸姿态角的功能函数为

G=A(x1,x2,…)-A*,

(2)

式中:A为实际姿态角;x1,x2,…,为影响弹丸姿态角的随机变量;A*为理想姿态角。笔者结合实际工程要求,设置预定值ΔA为0.2°,G<ΔA即为满足姿态角要求。

因此,协调输弹机机构可靠度和失效概率分别为

Rm=R(g>0∩G<ΔA),

(3)

Pf=1-Rm.

(4)

3 协调输弹机机构可靠性分析

3.1 可靠性分析

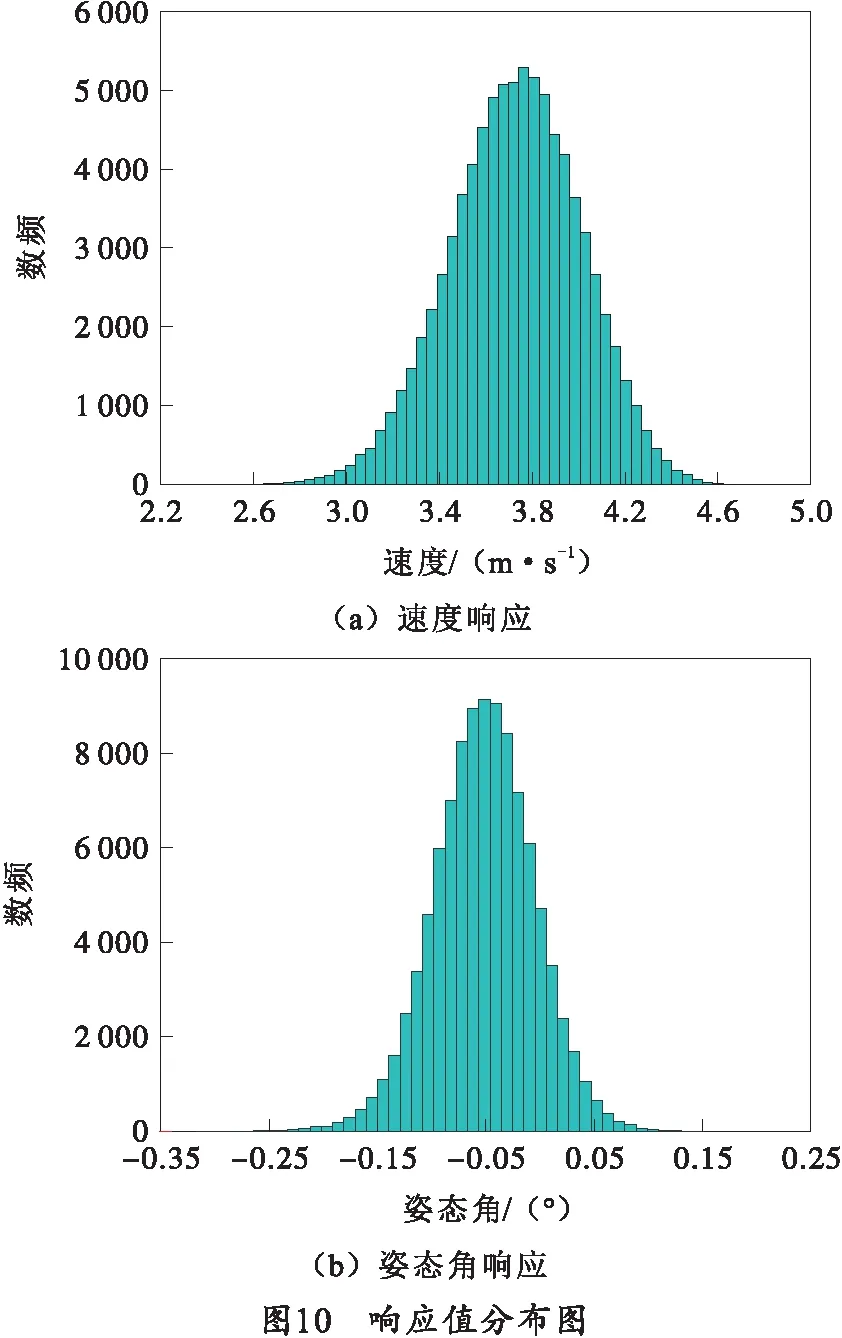
蒙特卡洛方法本质上为利用数学模型代替实际系统进行试验,以数字定量化的方式分析系统变化全过程[14]。笔者利用刚柔耦合动力学模型结合随机输入变量的分布规律,采用蒙特卡洛的方法抽取105个样本点,得到弹丸卡膛速度与姿态角的分布,如图10所示,可知,弹丸卡膛速度均值为3.697 976 m/s,标准差为0.271 317 m/s;弹丸姿态角度均值为-0.051 6°,标准差为0.046 1°。将刚柔耦合动力学仿真计算结果代入式(1)～(4)计算,协调输弹机机构可靠度为99.46%,失效率为0.54%。

3.2 可靠性灵敏度分析

输出结果对输入变量的响应程度常以灵敏度表征,可靠性灵敏度分析对可靠设计与优化起指导作用。利用协调输弹机可靠性仿真模型对各个参数对于可靠性的影响进行研究。可靠性灵敏度常以失效概率对输入变量的分布参数的偏导数表征:

(5)

式中,fx(x)为输入变量的联合概率密度函数。

协调输弹机机构可靠性均值灵敏度与标准差灵敏度分别为

(6)

(7)

式中:xj为第j个样本;N为样本数量;IF为指示函数;xji为第i个输入变量的第j个样本;μxi为第i个输入变量的标准差;σxi为第i个输入变量的标准差。

由于随机输入变量的单位不统一,需要对灵敏度进行无量纲归一化处理,均值灵敏度及标准差灵敏度无量纲化分别为

(8)

(9)

将3.1节中仿真数据与表1中数据代入式(5)～(9)中进行可靠性灵敏度分析计算,通过计算结果探究所选输入变量的均值与标准差对于协调输弹机机构可靠性的影响。均值灵敏度计算结果如图11所示,标准差灵敏度如图12所示。图11、12中的数值越大表示对协调输弹机可靠性的影响程度越大,灵敏度为正表示随着灵敏度数值的增加协调输弹机失效率增大,即协调输弹机可靠性降低。

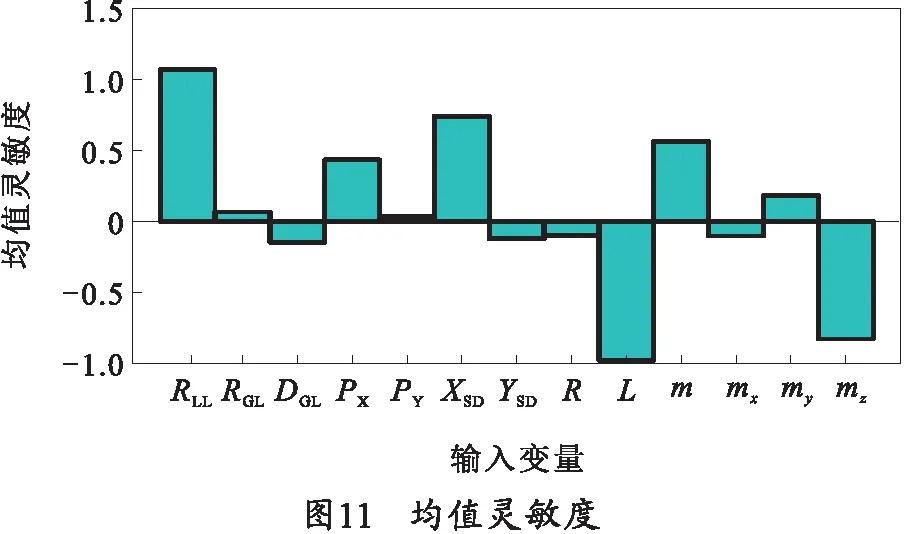
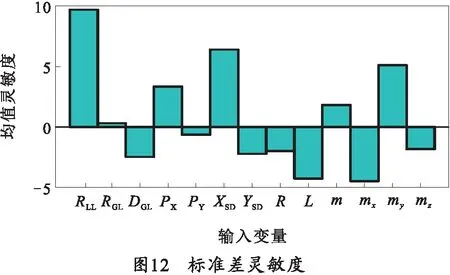
由图11～12可以看出,链轮基圆半径RLL、输弹盘焊接位置XSD、输弹盘长度L的均值与标准差对机构可靠性影响相对显著。随着RLL与XSD的均值与标准差数值增加,协调输弹机机构可靠性降低;随着L的均值与标准差数值增加,协调输弹机机构可靠性增大。

4 结束语

笔者根据协调输弹机的实际结构与0°射角工况,建立刚柔耦合协调输弹机动力学模型,采用蒙特卡洛法对刚柔耦合动力学模型进行数值模拟,获得了协调输弹机机构可靠度及可靠性的灵敏度。研究结果表明,在0°射角工况下,协调输弹机机构可靠性为99.46%,输弹盘焊接位置XSD、弹丸质心偏心mz、链轮基圆半径RLL、输弹盘长度L、弹丸质量m的均值对机构可靠性影响相对显著,链轮基圆半径RLL、输弹盘焊接位置XSD、弹丸质心偏心my、弹丸质心偏心mx、输弹盘长度L的标准差对机构可靠性存在显著影响。

笔者通过构建协调输弹机刚柔耦合动力学模型结合蒙特卡洛数值模拟对协调输弹机机构可靠性及灵敏度进行分析,可为今后可靠性优化提供参考。