基于Transformer算法的园区综合能源需求预测
2023-11-02尹宇晨刘宇杭马愿谦雷一
尹宇晨,刘宇杭,马愿谦*,雷一
(1.浙江理工大学 信息科学与工程学院,杭州 310018; 2.清华四川能源互联网研究院,成都 610200)
0 引言
随着全球经济的快速发展,人们对多元能源的需求持续增加,如冷热负荷需求。因此各国电力消费和需求呈现不同程度的快速增长[1]。但由于电能的存储特性,目前仍无法长时间储存电力资源,所以既要满足生产生活所需的电能,又要避免产生不必要的浪费。提高电力企业供电保持动态平衡的能力,否则居民日常生活、工业生产将受到严重影响。所以综合能源需求预测[2]在现代电力系统安全稳定经济运行中发挥愈来愈重要的作用。有效的综合能源需求预测可为一个地区电力系统发展规划做出指导,实现综合能源的高效生产及利用[3-4],同时保证电网的可靠运行和安全稳定。
伴随着园区多种能源形式耦合互补方式的不断成熟,关于综合能源需求预测的研究逐渐得到关注。短期负荷预测中,受气象变化、社会活动和节日类型等各种随机因素[5-6]的影响,在时间序列上,实际负荷的波动表现出较强的随机性,对预测精度的影响很大。
综合能源需求预测主要包括冷热电负荷预测。目前,电负荷预测的研究比较深入且已有大量的研究成果,主要集中于物理方法[7]及统计方法[8]。
物理方法根据用电负荷的区域范围、实时运行情况及四季变化等外界因素构建预测模型,模型复杂程度较高,实现难度大。
统计方法通过深入挖掘输入与输出间的内在联系,利用关联函数建立预测模型,对外界因素依赖程度明显降低,模型数学化程度更高,易于实现。例如,通过构建与时间相关的模型,即自回归(AR)模型[9]、滑动-平均模型(MA)、自回归积分滑动平均(ARIMA)模型[10]预测电负荷需求,上述模型对样本数据的需求较少,要求数据序列平稳;利用最小二乘法构建模型,搭配K-mean聚类算法改进的蝙蝠算法去优化最小二乘法支持向量机,提高预测精度[11],以及一些现代预测方法,如反向传播(Back Propagation,BP)神经网络[12]、随机森林算法[13]、基于专家预测和模糊贝叶斯[14-15]的预测方法等。其中,BP 神经网络通过将误差从输出层BP 到隐藏层和输入层,根据误差来更新网络参数,以逐步提高网络的性能。在深度学习领域具有广泛的应用,能够处理复杂的非线性关系,但容易陷入局部最优解并且对初始参数较为敏感。又如随机森林算法,虽然具有鲁棒性、高准确性、可解释性和对高维数据的处理能力等优点,但随机森林算法的缺点也包括训练时间较长、占用较大的内存空间和难以解释单个决策树的预测结果等。由于冷热负荷受到季节变化和气象变化的影响程度更大,与用户用能数据更为密切相关,以上的电负荷预测方法不能直接应用于冷热负荷预测,因此,一般通过构建时间序列模型或构建回归预测模型,采用自适应卡尔曼滤波等方法实现预测,缺少外界因素对负荷间影响的考虑[16-18]。
综上所述,本文提出一种基于Transformer 算法的综合能源需求预测方法,对冷热电负荷进行预测。考虑到冷热负荷受诸多因素共同影响,采取Pearson 相关性分析、最小误差理论筛选影响因素进行筛选。其次,建立基于欧式距离的相似日选取方法作为相似度的度量标准。然后,将相似日负荷、历史负荷、已筛选3 维影响因素相关数据作为输入数据,采用Transformer 模型进行负荷预测。最后,以中国东部某园区为例进行实证分析,验证了基于Transformer算法的园区综合能源需求预测方法的正确性、合理性和可行性。
1 冷热电负荷的影响因素
1.1 冷热电负荷的影响因素
短期冷热电负荷预测中,受气象变化、社会活动和节日类型等各种随机因素的影响,在时间序列上实际负荷波动的随机性较强。适当的输入变量直接与模型的预测性能相关,影响因素的合理选取有利于提高预测模型的有效性和可靠性。
气象因素对冷热电负荷影响很大,为降低模型的复杂程度。本文拟选取温度、湿度、风速3个气象因素,以及各气象因素的最大值、平均值、最小值,共计9 维影响因素,作为预测模型的影响因素来考虑,表示为
式中:H为影响因素集合;hi为第i个影响因素向量;n为影响因素个数,文中n= 9。影响因素选取如图1所示。
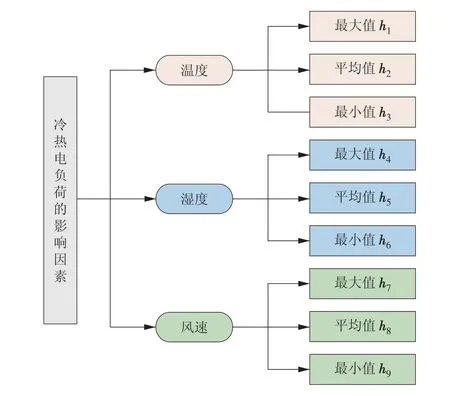
图1 影响因素的选取Fig.1 Selection of influencing factors
1.2 数据预处理
由于各种随机因素的影响,使采集到的冷热电负荷需求的影响因素数据出现缺失或异常值(例如0 或空值)。若使用带有缺失或异常值的数据,将一定程度上使得预测结果出现误差,准确性较低。因此,进行负荷预测前,需要对数据进行预处理和修正,采用平均插值法对缺失或异常数据进行修复和补齐,平均插值法计算式为
式中:xi为经过修复或补齐后的数据;xi-1和xi+1为缺失或异常数据前后的数据。
对数据进行规范化处理是负荷预测流程中的前提,考虑到不同影响因子的量纲不同。利用最值法对影响因素进行归一化处理,以除去量纲差异对预测结果所带来的影响,归一化计算方法为


1.3 基于Pearson 系数的综合能源需求影响因素相关性分析
基于上述的负荷影响因素的分析,短期冷热电负荷预测中,易受气象变化、社会活动和节日类型等各种随机影响因素的影响。为了简化建模难度和模型复杂程度,本文基于Pearson相关性分析[18]对初步选取的9 维影响因素进行相关性筛选,利用误差最小原则选择冷热电负荷对应的3维影响因素用以相似日的选取。
基于Pearson 系数的冷热电负荷影响因素的相关性,定义影响因素和负荷之间的Pearson 系数,如式
式中:cov(Xi,Xj)为变量Xi,Xj的协方差;σXi,σXj分别为Xi,Xj的标准差;ρ(Xi,Xj)为2 个变量Xi,Xj之间的相关系数,其取值范围为[-1,1]。Pearson 相关系数ρ描述相关性强弱如下:
(1)当Xi,Xj2个变量无关时,ρ= 0。
(2)当Xi,Xj2个变量正相关时,0 <ρ≤1。
(3)当Xi,Xj2个变量负相关时,-1 <ρ≤0。
2 综合能源需求相似日选取
复杂的气象状况使得负荷预测的难度极大提升,因此合理地选取预测相似日是提高负荷预测模型预测效果的有效途径。相似日的选取在负荷预测算法中起到了特征提取和负荷波动分析的重要作用,能够显著提高负荷预测的准确性和可靠性。
通过分析相似日的负荷模式和特征,可以帮助提取与负荷相关的特征。通过设定阈值并选取相似度最大的某日作为相似日,将相似日的负荷数据作为影响因素的相关输入数据,可以有效地提高负荷预测模型的准确性和性能。
此外,选取相似日还可以用于负荷波动的分析和预测。相似日的负荷数据提供了有用的参考,能够帮助我们理解负荷的季节性、周期性以及特殊事件对负荷的影响,从而更好地进行负荷预测。
欧氏距离是最常用的距离计算公式,衡量的是多维空间中各个点之间的绝对距离,当数据很稠密且连续时,这是一种很好的计算方式。
设待预测日的影响因素为W={W(k)|k=1,2,3,…,z},其他日期的影响因素为E={Ek(j)|j=1,2,3,…,m;k= 1,2,3,…,z}。
计算不同影响因素与对应待预测日的气象因素之间的欧氏距离为
式中:dk(z)为待预测日的第k个影响因素与日期z对应的影响因素之间的欧氏距离。
同时,考虑到不同的影响因素对冷热电负荷影响程度不同,故结合Pearson相关系数综合计算。将计算出的欧氏距离分别与得到的各影响因素的Pearson 相关系数对应相乘,并将同一天的结果进行累加,得到一个每天的综合分数
式中:rk为Pearson相关系数。
综合分数表示某日与待测日之间的相似程度。将综合分数从低到高排序,分数越低的日期与待预测日的相似度高。本文选取待预测日之前5个分数最低的日期作为相似日。
通过上述Pearson 相关性分析筛选的3 维影响因素及待预测日与各样本日对应影响因素的综合相似度,设定阈值ε选取相似日,其中相似度最高的某日即为相似日。阈值设定方法为
3 园区综合能源需求预测
3.1 基于Transformer算法的综合能源预测结构
综合能源需求预测需对冷热电负荷进行并行预测。Transformer算法是一种基于全连接层和自注意力机制的结合体,是一种避免无意义循环的模型结构,完全依赖于其注意力机制对输入输出的全局依赖关系进行建模。主要通过编码器-解码器的形式进行时间序列预测,并行性好,可有效得到最优结果。考虑到Transformer 算法在时间序列预测中也有很好的结果。利用Transformer 进行综合能源需求的预测优势在于突破了RNN 等预测算法模型不能并行计算的限制[19]。相比其他算法,计算2 个位置之间的关联所需的操作次数不随距离增长[20-24]。Transformer网络结构如图2所示。
自注意力机制是Transformer 算法的核心。自注意力可以产生更具可解释性的模型。可从模型中检查注意力分布。即给输入的数据编入位置向量后通过3 个权值矩阵WQ,WK,WV转换成自注意力机制所需要的Q,K,V向量,并计算自注意力机制值。
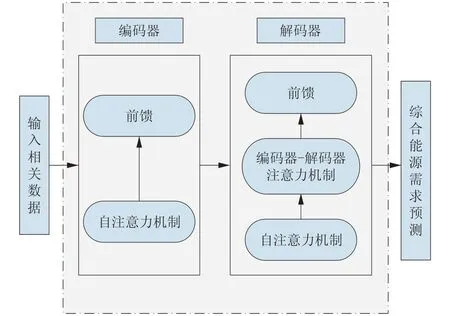
图2 Transformer网络结构Fig.2 Transformer network structure
Transformer仅通过自注意力机制算法得到综合能源的预测结果之一,同时Transformer 的多头注意力机制可将算法重复多次,得到一个更均衡、更贴合目标的结果。在训练预测过程中,Transformer 内部可以通过对给出的数据进行学习与训练,有效地提取数据内在信息,并在进行预测训练时对原有的数据进行遮掩,以让算法的预测更具有说服力。通过Transformer 的注意力机制和编码器-解码器的形式,可以有效提升算法在长时间序列预测的速度,同时避免陷入循环,有利于快速准确得到预测结果。
Transformer 算法是一种强大的序列建模方法,在自然语言处理领域取得了重大突破。此算法同样适用于其他序列预测任务,如能源需求预测。
本文中运用Transformer 算法来捕捉能源需求与各种相关因素之间的复杂关系。具体而言,通过将历史能源需求数据作为输入序列,并结合其他相关数据以及时间信息(如季节性、节假日等)构建一个综合的输入表示。
接下来,将详细描述Transformer 算法在能源需求预测中的应用过程。使用Transformer 的编码器-解码器结构,其中编码器将输入序列映射到1 组高维向量表示,解码器根据编码器的输出生成目标序列的预测结果。采用自注意力机制,使模型能够同时关注输入序列中的不同位置,并捕捉序列中的长期依赖关系。
为了将Transformer 算法与能源需求预测相结合,本文将预测任务定义为回归问题,并使用均方误差(MSE)作为损失函数,然后通过对模型进行训练和优化,调整模型参数以最小化预测结果与真实能源需求之间的差异。
Transformer 算法在能源预测中的具体作用如下。
(1)输入表示:Transformer结构的输入由历史能源需求数据及其他相关数据(如天气数据、人口统计数据等)组成。这些数据构成了模型的输入序列,用于捕捉能源需求与各种相关因素之间的关系。
(2)编码器:Transformer结构中的编码器负责将输入序列映射到一组高维向量表示。编码器通过自注意力机制,使模型能够同时关注输入序列中的不同位置,并捕捉序列中的长期依赖关系。编码器的输出被传递给解码器进行下一步处理。
(3)解码器:解码器接收编码器的输出,并根据其生成能源需求的预测结果。解码器通过自注意力机制和对编码器输出的注意力机制,对输入序列进行动态加权,并生成与预测相关的上下文表示。最终,解码器利用这些上下文表示生成能源需求的预测结果。
(4)损失函数与优化:能源需求预测模块使用预测结果与真实能源需求之间的差异作为损失函数。常用的损失函数是MSE,用于衡量预测结果与真实值之间的平均平方误差。通过BP 和优化算法(如随机梯度下降),模型调整参数以最小化损失函数,从而提高预测准确性。
Transformer 结构通过编码器和解码器的组合,将输入序列映射到能源需求的预测结果。编码器捕捉输入序列的特征表示,解码器根据这些表示生成预测结果。能源需求预测模块通过优化过程,使预测结果尽可能接近真实值,从而实现对能源需求的准确预测。
综上所述,基于Transformer 算法的园区综合能源需求预测步骤如下。
(1)将数据按照时间序列排序并导入编码器中,并添加位置编码。
(2)编码器中的多头注意力机制和全连接神经网络对数据进行处理,通过自注意力机制算法得到编码器输出值。
(3)重复(2)操作n次(n为编码器数量),将得到的数据导入解码器。
(4)在解码器中训练并预测结果,达到设定的终止条件,否则继续训练预测。
(5)经过一次线性变换,然后归一化得到输出的概率分布。
3.2 基于园区综合能源需求预测流程
考虑到园区用户内不同时间对综合能源的需求,选取考虑因素和相似日,利用Transformer,对综合能源的需求进行预测,预测流程如图3所示。
具体步骤如下。
(1)收集关于综合能源负荷数据及影响因素历史数据等,选取具有代表性的数据,进行归一化、插值预处理。
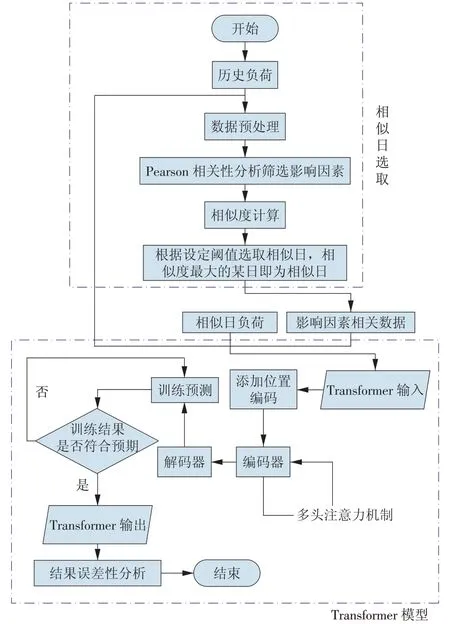
图3 基于Transformer的综合能源预测方法流程Fig.3 Flowchart of an integrated energy forecasting method based on Transformer
(2)通过Pearson 相关性分析对初步选取的9 维影响因素进行初步分析,同时利用误差最小原则筛选出冷热电负荷对应的3维影响因素用以相似日的选取。
(3)相似度计算,利用欧式距离公式计算冷热电负荷序列相似度,通过预先设定的阈值选取相似日。
(4)选取相似日负荷、历史负荷、已筛选3 维影响因素相关数据作为输入,输入到Transformer 模型中,添加PE位置编码,在编码器中进行编码,并计算出K,Q,V的值,从而算出Z矩阵并拼接,继续进行下一层编码。将最后的结果输入解码器。
1)输入相似日负荷、历史负荷、已筛选3维影响因素相关数据之间的相关性得分,计算相关性得分使用点积法,就是用Q中每一个向量与K中每一个向量计算点积。具体公式如下
2)对于输入序列中各特征之间的相关性得分进行归一化,目的是训练时梯度能够稳定。具体公式如下
式中:dK是K的维度。
3)利用归一化函数,将每个输入值之间的得分向量转换成[0,1]之间的概率分布,同时更加凸显各输入值之间的关系。经过归一化后,得分转换成1个值分布在[0,1]之间的矩阵,记作P。
4)根据冷热电负荷输入之间的概率分布,然后乘对应的V值,P与V进行点积。
整体计算公式为
(5)调整合适参数,根据得到的数据对要求数据进行训练预测,并检验预测结果。
(6)设定成功率阈值,当达到阈值R或已经达到训练最大次数时停止,输出预测结果。
(7)对预测结果进行误差分析,选用平均绝对百分比误差MAPE来评价
式中:xi为综合能源需求的实际值;yi为综合能源需求的预测值。
4 实例分析
为验证所提预测方法的有效性以及预测精度等指标,本文采用我国东部某园区的冷热电负荷及其相关影响因素进行实例分析。该园区冷热电负荷序列如图4所示。
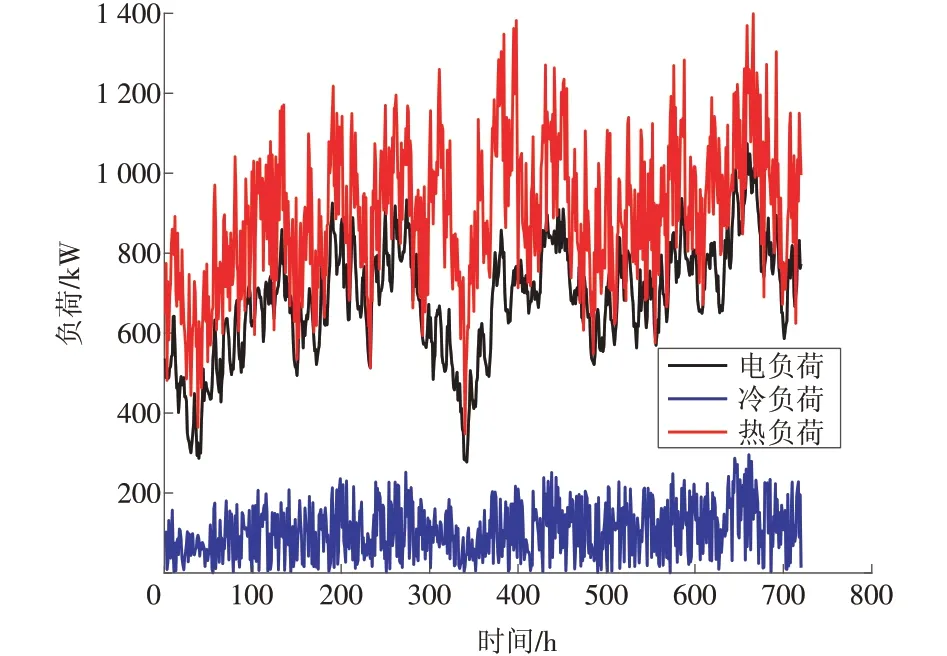
图4 园区冷热电负荷序列Fig.4 Heating, cooling and electricity load series
采用该园区12 月份的冷热电负荷及其相关影响因素的数据作为初始样本,样本数据的间隔时间是1 h,每天24 组数据,共计720 组数据,选取前600组数据作为输入训练数据,后120 组数据作为测试数据验证算法的预测准确度。
4.1 影响因素的影响比例
上文提到选取9 维冷热电负荷影响因素采用Pearson相关性分析选取,如图5所示。
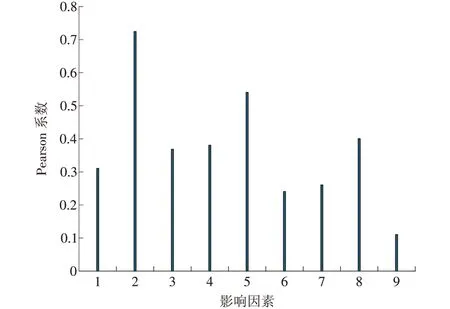
图5 电负荷Pearson相关性分析Fig.5 Pearson correlation analysis of electricity load
为避免误差,由Pearson 相关性分析,选取相关性最大的3 个影响因素作为电负荷模型输入。电、冷和热负荷影响因素见表1。
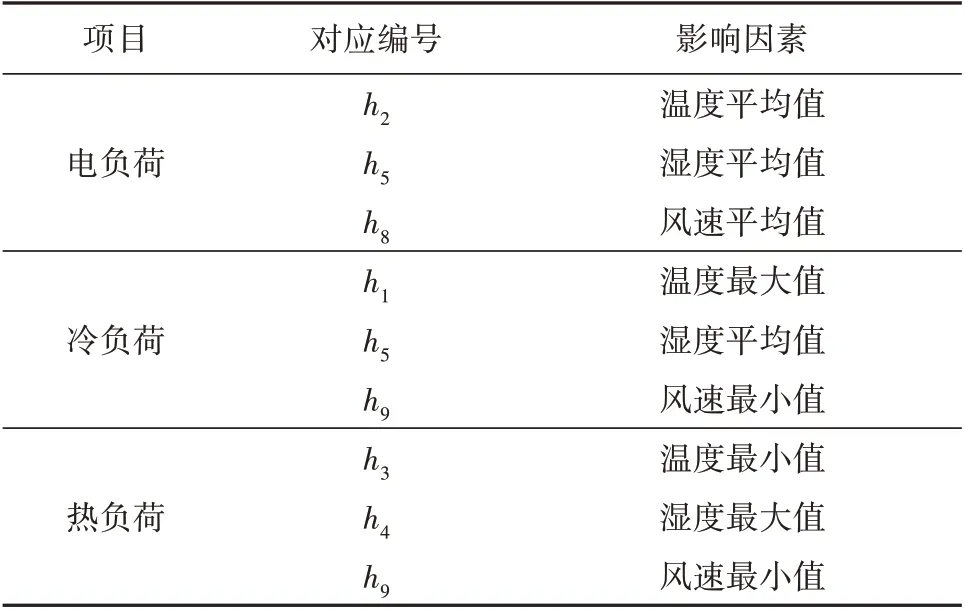
表1 负荷影响因素Table 1 Selection of factors affecting electricity load
表1表明,电、冷、热负荷的影响因素不尽相同,很有必要进行因素的再次选取。
4.2 相似度计算
利用欧式距离公式计算冷热电负荷序列相似度,通过预先设定的阈值选取相似日,设定阈值为ε= 10。
本文以2016 年12 月1 日至12 月30 日共计30 d数据为训练数据,以12 月31 日为待预测日。由于Transformer 算法在预测时会对待预测数据进行隐藏,不存在数据泄露的可能,可以认为预测出的数据具有真实、可靠性。电、冷、热负荷欧氏距离如图6—8所示。
从图6—8中可以得到,冷热负荷数据达到指定阈值的比例远高于电负荷数据达到阈值的比例,即电负荷相比前两者,更具有随机性。
4.3 综合能源需求预测结果分析
根据上述结果,将数据导入模型进行预测分析,并独立进行10个试验以取结果的平均值。冷热电负荷预测结果如图9—11所示。
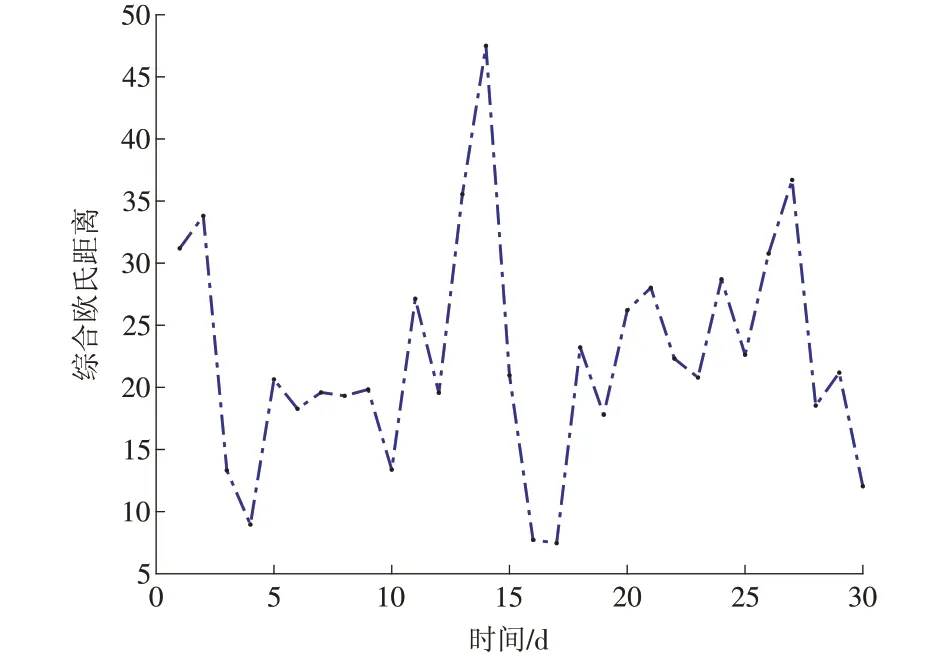
图6 电负荷欧氏距离Fig.6 Electricity load Euclidean distance

图7 冷负荷欧氏距离Fig.7 Cooling load Euclidean distance
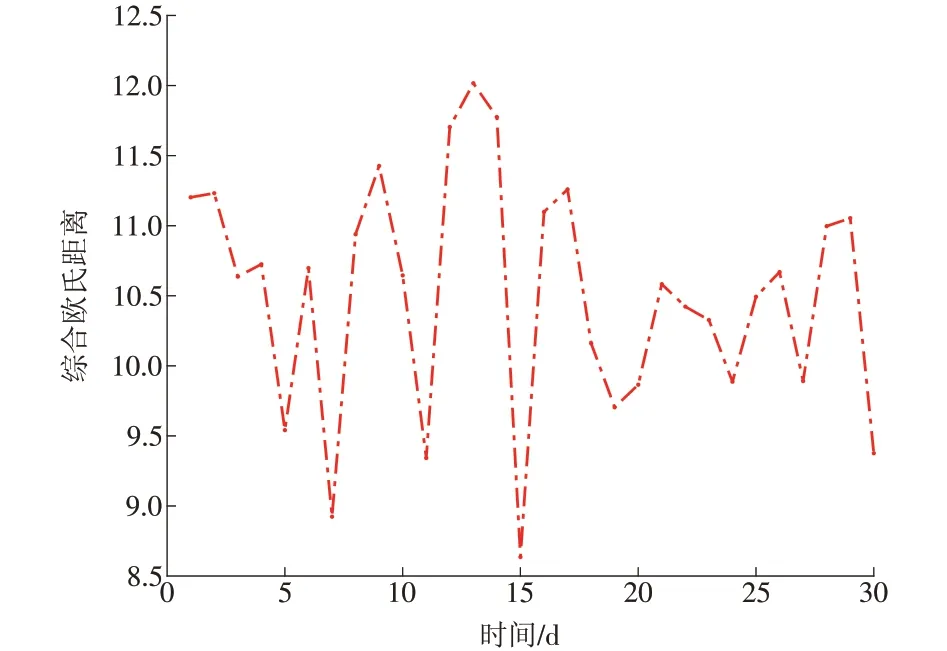
图8 热负荷欧氏距离Fig.8 Heating load Euclidean distance
3 种负荷总体预测结果上来看,随机森林算法、BP 算法和Transformer 算法预测结果和真实值进行对比,显然Transformer 显示的数据总体上更接近真实值,相似性更强。
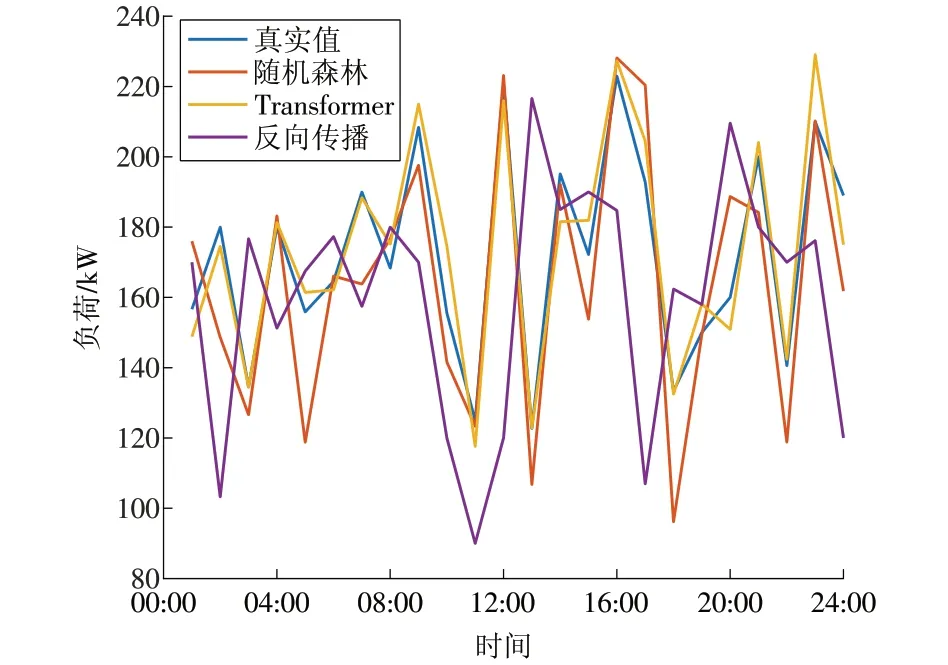
图9 冷负荷预测结果Fig.9 Cooling load forecasting results
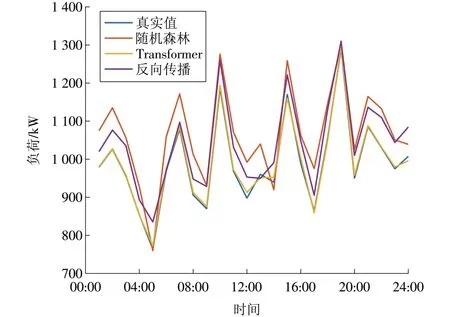
图10 热负荷预测结果Fig.10 Heating load forecasting results
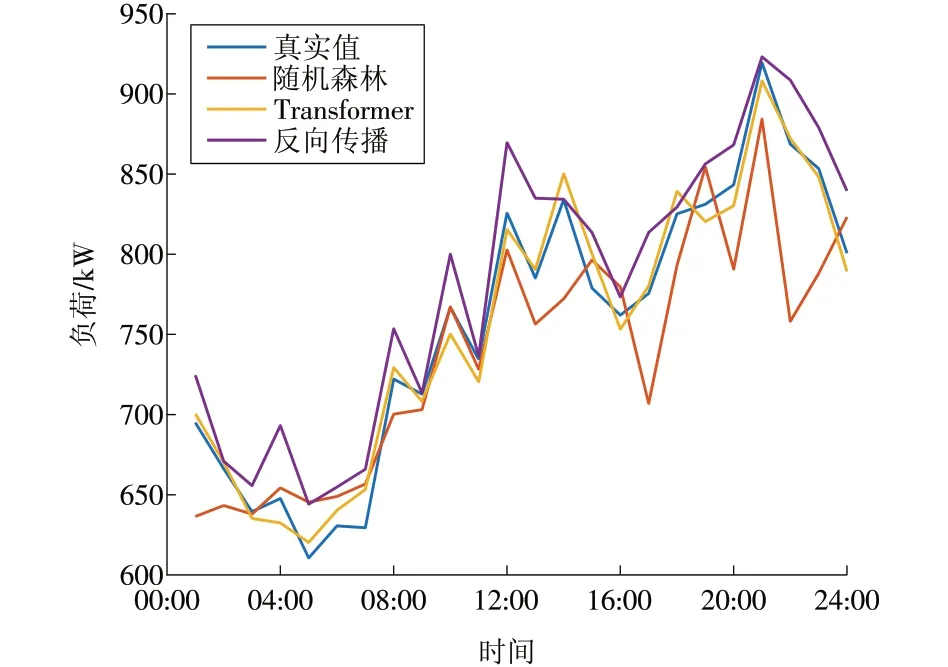
图11 电负荷预测结果Fig.11 Electricity load forecasting results
根据冷负荷预测结果显示,冷负荷需求在一天24 h 内整体呈现出波动振荡的趋势,峰谷现象较为明显。预测结果的负荷曲线在很大程度上反映了这一趋势,并且在大部分时间段与实际负荷需求曲线相符合。这在一定程度上得益于之前提取的相似日数据,这些数据有助于Transformer 算法进一步准确地进行预测。从冷负荷的设备用能特性来看,其功率需求指的是设备在运行过程中所需要的电功率。不同冷负荷设备在不同的运行状态下,其功率需求会有所变化。例如,空调系统在制冷启动阶段通常需要较高的功率,而在保持温度稳定的运行阶段功率需求较低。因此,在冷负荷需求曲线上体现为峰谷振荡的现象。当设备启动运行时,冷负荷需求量较大,呈现为峰值;而在维持稳定运行时,冷负荷需求量较低,呈现为谷值。
根据热负荷预测结果显示,热负荷需求在一天的24 h 内整体呈现出小范围波动振荡的趋势,与冷负荷相比,峰谷值差异较大。通过与真实值的对比可以看出,由于选取了冬季负荷数据,3 种预测方法的热负荷曲线相对于冷负荷更加符合真实负荷曲线,而不仅仅是Transformer 算法单独趋近于真实值。然而,就精确性而言,Transformer算法仍略胜于其他2 种方法。从热负荷的设备用能特性来看,热负荷的设备主要与供热系统和热能转换设备相关。例如,供热管道和散热器的工作方式取决于具体的供热系统设计和需求。选取冬季数据的原因是冬季负荷具有较高的整体需求量。不同的供热系统可能采用间断性工作或持续工作方式,以满足不同的供热需求。整体而言,热负荷需求曲线的峰谷值差异相对于平均负荷水平的波动量没有冷负荷那么明显。
而电负荷预测结果显示,整体上负荷需求呈现出时段性变化。在00:00 — 07:00,负荷需求相对较低,随后逐渐上升。通过与真实值的对比可以看出,相对于其他2 种算法,Transformer 算法在电负荷预测方面具有更高的准确性,更接近真实值。从电负荷的设备用能特性来看,常用的用电设备种类繁多,涵盖了不同领域和行业的需求,例如办公设备、生产设备、照明设备等。在00:00 — 07:00时段,电负荷总体较为低迷,相较于白天活跃期明显较少。此外,负荷变化的波动也很大程度上与人们的社会生产和活动密切相关。
最后,对预测结果进行误差分析,选取平均绝对误差百分比MAPE进行评估,结果见表4。在多个预测算法中,本文选取的Transformer 算法更符合,其起伏趋势更接近实际数据。特别是在冷负荷预测中,Transformer 算法预测结果的平均绝对百分比误差明显优于其他2种算法。鉴于本文选择的是冬季负荷数据,考虑到气候因素的影响,整体而言,3种预测方法中冷负荷预测的误差明显更大,而热负荷预测的误差明显较小。此外,与其他2 种预测方法相比,本文所采用的Transformer 算法在热负荷预测曲线的稳定性和拟合性方面稍显优势。
由表4可以看出,在冷热电负荷方面,该预测模型展现出良好的预测能力。相较于中长期序列模型,该模型具有独特的优势,并且与待预测日的负荷具有极高的相关性,因此适合作为预测模型的输入。然而需要指出的是,本文仅选择了12月份的数据进行预测,这在一定程度上是基于冬季冷热负荷的特殊性。
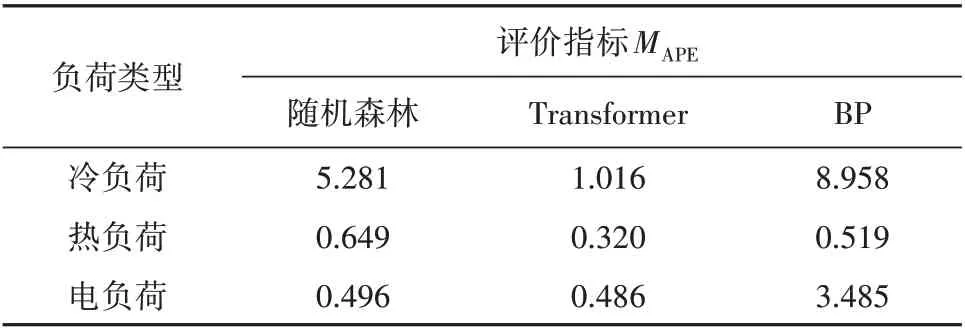
表4 综合能量预测结果评估Table 4 Electricity load forecasting results %
5 结论
针对目前综合能源相关预测方向的不足,本文构建出一种基于Transformer 的时间序列预测模型,通过模型构建与预测,与实例对比分析后得出以下结论。
(1)针对冷热负荷受部分外界因素影响较大,对影响综合能源的影响因素进行分析,根据Pearson相关性分析进一步确定影响因素。
(2)提出了基于Transformer 算法的时间序列预测模型,通过算法对综合能源需求进行预测并分析。
(3)采用在时间序列预测上有明显优势的Transformer 算法,并采用相似度负荷特征作为输入对预测模型进行优化,提高预测精度与可靠性。
结果达到预期,但不具有普适性,后续可对其余季节月份进行预测训练,使模型更完善,结果更具有通用性。
