一种基于有限密钥和诱骗态的双场量子密钥分发协议
2023-11-02赵胶胶
康 鹏 郭 翔 赵胶胶
1(贵州电网有限责任公司电力调度控制中心 贵州 贵阳 550000)
2(南京信息工程大学计算机与软件学院 江苏 南京 210044)
0 引 言
随着我国电力系统的不断完善,电力系统的调度工作也在被持续不断地更新和健全。它对于整个电力系统来说,是一项纪律严格、技术复杂的管理工作。面对电力系统不断变化的要求和挑战,电力系统调度工作是否到位,直接影响着电力系统能否安全运行。
量子密钥分发(Quantum Key Distribution,QKD)[1]被认为是量子信息科学最成熟的应用,其安全性由量子物理原理保证,可为支持电力调度提供安全保障,但是量子通道中光脉冲的传输损耗极大限制了合法用户之间的通信距离[2]。
为了突破信道传输的局限性,提出了量子中继器方案[3-4],但是用当前的量子通信技术来实现量子中继器是不切实际的。2012年,Lo等[5]提出了与测量设备无关的量子密钥分发(Measurement-device-independent Quantum Key Distribution,MDI-QKD)协议,该协议不仅去除了所有探测器侧通道,而且使传统激光器的安全距离增加了一倍。尽管如此,MDI-QKD也无法突破长距离量子通信的限制。
2018年,Lucamarini等[26提出了双场量子密钥分发TF-QKD,该协议被认为可以克服在没有可信中继的情况下速率-距离的限制。基于不受信任节点的分光器的单光子干扰,TF-QKD的秘密密钥率相对于传统的MDI-QKD相位编码方案进行了二次改进[7]。随后,许多学者根据秘密密钥率与信道传输的平方根成比例的优势,提出了TF-QKD协议的多种变体,同时也提供了更严格的安全证明[9-11]。之后,通过对这些变体协议进行相关的实验,证明了使用当前技术进行TF-QKD的可行性[12]。尽管如此,理论与实际之间仍然存在不可避免的差距。在这些实验局限性中,有限密钥效应[13]是估计最终秘密密钥率不能忽略的特征。目前,提出了几种有限密钥分析来研究TF-QKD[14]的实用性。另外,另一个实验局限性是光子源的不稳定性。在原始TF-QKD协议中采用的是稳定光源,而在实际系统中始终发出的光子脉冲,其强度无法渐近地用恒定值代替[15]。
在本文中,我们提出了一种基于有限密钥和诱骗态的TF-QKD协议。利用不同的统计波动分析模型[16-18]执行两个诱骗状态TF-QKD协议的参数估计步骤。在通用可组合框架[19]的基础上,得到统计波动限制的严格的秘密密钥率。在没有强度波动的情况下,我们通过对变体统计波动分析工具估算的最终秘密密钥率进行了简要比较。在分析强度波动对协议性能影响时,我们利用Azuma不等式[20-21]分析了严格的有限密钥,证明了在强度波动的情况下,针对一般攻击的可组合安全性。通过数值模拟,我们研究了具有统计波动和强度波动的不同总信号脉冲的秘密密钥率。仿真结果表明,强度波动对实际诱骗态TF-QKD协议的性能影响不可忽略。
1 基于有限密钥和诱骗态的TF-QKD协议
虽然Grasselli等[22]提出的实用诱骗态TF-QKD方案,只需设置两个诱骗强度就足以击败通道的点对点私有容量,并且该协议可有效对抗光脉冲的强度波动,但其安全性是基于无限密钥和稳定光子源的假设。由于受通信时间、存储能力等因素的限制,所以量子通信中通信双方传输的脉冲数是有限的。为了解决该问题,我们提出了一个基于有限密钥和诱骗态的TF-QKD协议,具体步骤如下。
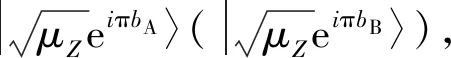
步骤2密钥分配。根据基的选择,Alice和Bob通过量子通道分别将其光脉冲发送给不受信任的第三方Charlie。
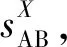
步骤4步骤重复。将步骤1、步骤2和步骤3重复N次,使双方都获得了足够多的成功检测事件。在这种情况下,可以进行下面的密钥筛选步骤。
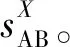
(1)
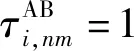
(2)
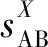
(3)
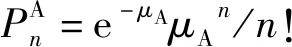
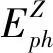
(4)
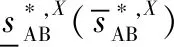
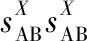
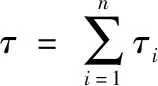
(5)
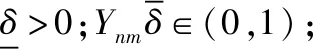
(6)
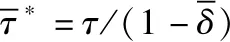
(7)

(8)
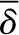
(9)
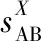
(10)
(1) 当Alice和Bob分别发出n和m个光子态时,我们利用文献[22]中提出的诱骗态法,对Y0,0、Y2,0、Y0,2和Y1,1的上界进行推导。
(11)
其中:
(12)
将文献[16]中提出的诱骗态法应用于式(11),则Y1,1的上界为:
(13)
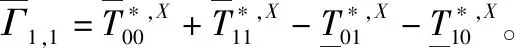
Y2,0和Y0,2的上界为:
(14)
其中:
(15)
为了得到Y0,0的上界,我们需要知道Y2,2的下界和Yn,0和Y0,m的上界。
Yn,0和Y0,m的上界为:
(16)
所以Y2,2的下界是:
(17)
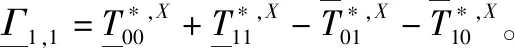
从而我们可以得到Y0,0的上界:
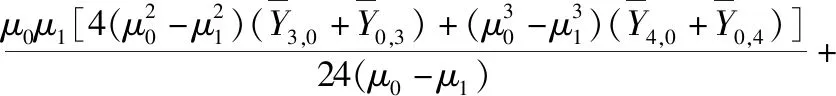
(18)
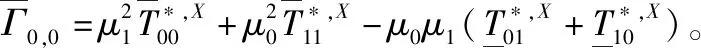
根据文献[11]中提出的估计方法,TF-QKD协议的X基上比特误码率的上界为:
(19)
其中:
(20)
(21)
式中:ε″是失败的概率。
(22)
步骤7密钥纠错。为了获得相同的密钥位串,Alice和Bob实施了信息协调方案,他们通过lEC位执行纠错步骤。此后,Alice使用字符串ZA的log2(1/εcor)位执行随机通用哈希函数,并将哈希发送给Bob。如果Bob的字符串ZB的哈希值与ZA的哈希值不同,则中止该协议。
步骤8隐私扩大。为了确保信息泄漏得到控制,他们利用一个随机通用哈希函数来提取一个长度为l的私有密钥字符串。
2 协议安全性分析
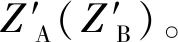
(23)
如果满足以下条件,则最终密钥满足安全性:
(24)
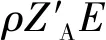
在本文中,我们通过使用文献[17]和文献[22]中提供的诱骗态法求出秘密密钥字符串长度l来获得秘密密钥率R。根据通用组合框架定义[19],我们提供了秘密密钥长度的详细估计,过程如下所示。
E′首先总结了Eve学习到的有关Alice原始密钥字符串ZA的全部信息,通过利用随机通用哈希函数,可以从ZA中提取长度为l的εsec密钥:
(25)
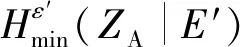
(26)
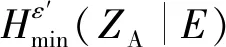
(27)
(28)
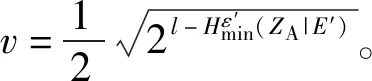
(29)
为了保证协议的保密性,错误项都被固定为一个常数:
(30)
因此εsec=13ε1。
如果最终密钥的长度l满足以下要求,则有限密钥体制中的实用TF-QKD协议为εsec:
(31)

3 协议性能分析
除了有限密钥效应外,TF-QKD的另一种实现是光子源的强度波动。因为我们在TF-QKD系统上应用了具有两种诱骗态的方法,因此应同时考虑信号脉冲和诱骗脉冲的强度波动,在没有强度波动的情况下,我们假设检测事件是独立的。但是,当光子源不稳定时,如果窃听者Eve采取相干攻击,则光脉冲的强度可能与其他脉冲相关。在这种情况下,不满足检测事件的独立条件。为了估计光子源强度波动与产生的秘密密钥率之间的关系,我们利用Azuma不等式[20-21]对相关样本进行有限密钥分析。
在实用TF-QKD协议中,信号脉冲和诱骗脉冲采用三种不同的强度。本文假设信号脉冲和诱骗脉冲的强度波动幅度对Alice和Bob相等且对称。
(32)
式中:μi是诱骗脉冲的强度,i∈{0,1}和δμ表示强度的波动幅度。
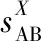
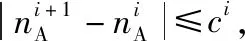
(33)
式中:δ∈(0,1)。
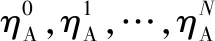
(34)
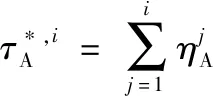
(35)
(36)
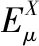
4 数值模拟
为了验证我们的协议在不稳定光子源强度波动下的性能,本节主要从以下四个方面进行了模拟实验:第一,不同的信号脉冲总数;第二,秘密密钥率的估计方法;第三,不同的强度波动;第四,不同数量的总信号脉冲。我们的协议在实际应用场景中,相位失调不会因为诱骗脉冲的相位随机化而影响相位误码率。在这种情况下,光脉冲通过量子通道后的偏振和相位失调被固定为2%,这与原来实用TF-QKD协议[22]相同。
在图1中,我们使用乘法Chernoff界模拟了具有有限密钥大小的TF-QKD的秘密密钥率,演示了该协议在不同信号下的性能。图1显示了检测器的暗计数率Pd分别为10-8、10-7和10-6时,秘密密钥率与损耗之间的关系,实线、虚线和点状虚线对应的信号脉冲总数分别为N=10x(x=12,13,14)。如图1所示,当暗计数率较小时,有限密钥效应较为显著。
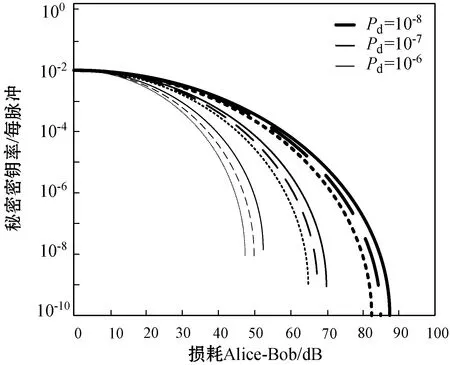
图1 检测器的暗计数率Pd分别为10-8、10-7和10-6时,秘密密钥率随损耗的变化
为了找出TF-QKD协议最严格的分析界限,我们比较了Hoeffding不等式、乘法Chernoff界[17]和改进型的Chernoff界[18]的性能。在图2中,线的粗细用来区分利用Hoeffding不等式,乘法Chernoff界和改进型的Chernoff界进行的参数估计。为了进行比较,我们考虑了两个不同总数的信号脉冲,N=1013(虚线)和N=1014(实线)。如图2所示,利用改进型的Chernoff界是三种不同估计秘密密钥率方法中最严格的,但是在信号脉冲总数较大时,其优点不是很明显。

图2 分别利用Hoeffding不等式、乘法Chernoff界和改进型的Chernoff界估计的秘密密钥率与损耗的关系
在光子源不稳定的情况下,我们评估具有不同强度波动幅度的秘密密钥率。模拟结果表明,强度波动的影响在现实生活中是不可忽略的。我们将暗计数率固定为Pd=10-8,信号脉冲的总数固定为N=1015,因此,通过采用不同的方法可获得如图3所示的从左到右的曲线强度波动幅度(分别为δμ=0,0.1,0.2,0.3)。可以看出,当强度波动幅度为δμ=0,0.1,0.2时,该协议可以超越PLOB界线,但如果δμ过大,协议则无法超越PLOB的界线。
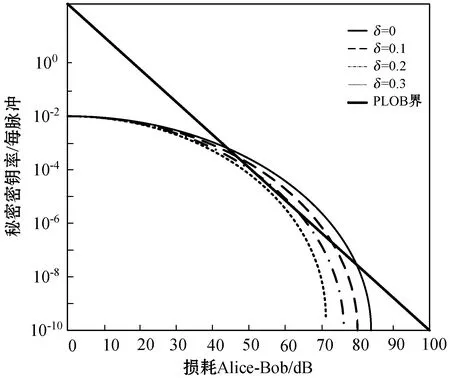
图3 对于不稳定信号源,在不同强度波动幅度下,针对总体损耗的秘密密钥率
为了评估强度波动对信号脉冲总数的影响,我们在给定δμ的情况下,估算了具有不同数量的总信号脉冲的秘密密钥率。在图4中,从左到右的曲线是针对不同数量的总信号脉冲获得的(N=10x,x分别为13,14,15,16)。结果表明,当总信号脉冲的数量较小时,δμ的影响非常显著。
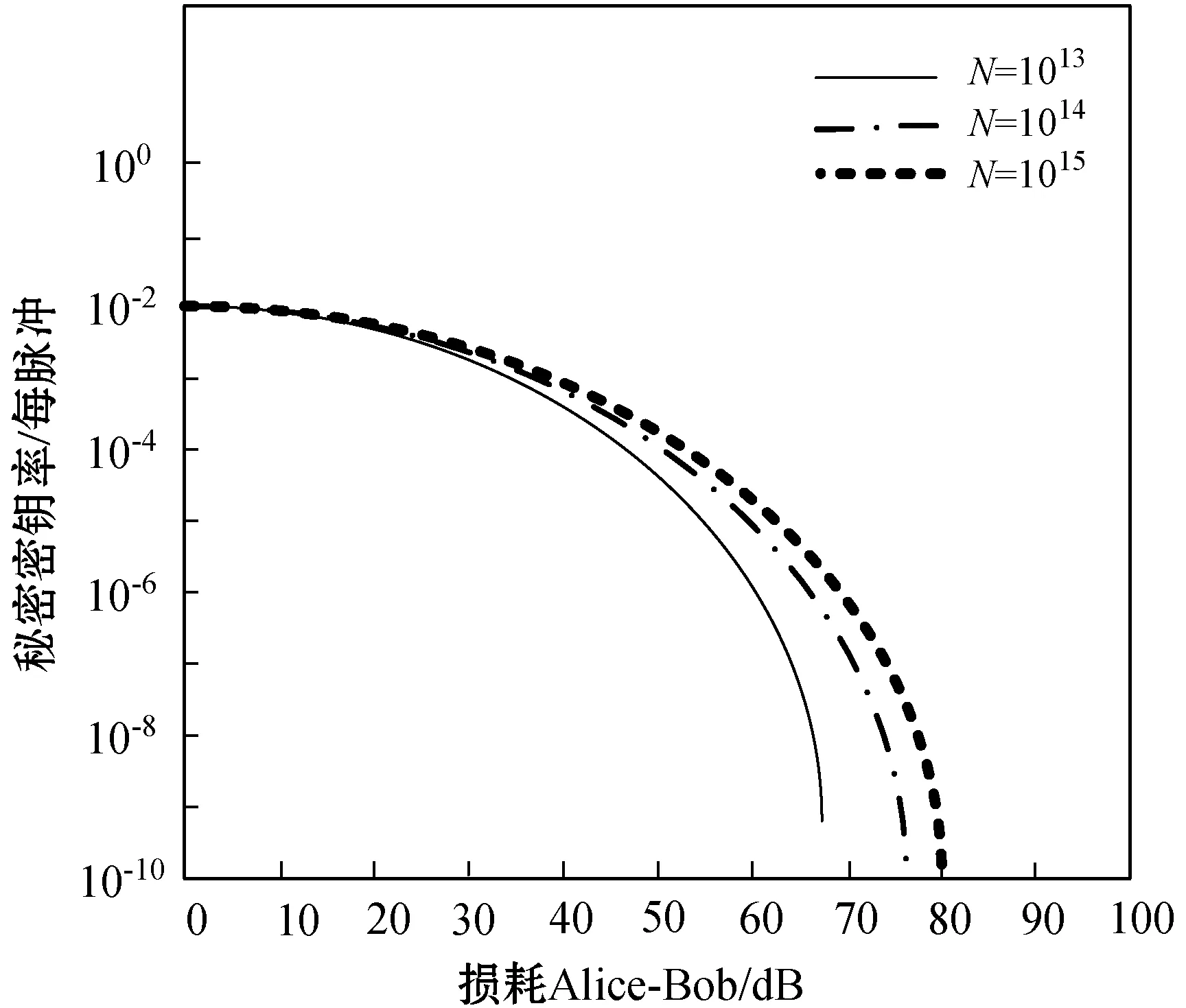
图4 对于强度波动幅度δμ固定为0.1的信号脉冲的不同数据大小,秘密密钥针对总损耗的比率
5 结 语
本文分析了具有有限密钥和强度波动的实用TF-QKD协议的性能。基于系统的对称假设,我们利用通用可组合框架推导出了密钥长度公式。利用统计波动的估计值,求出X基中成功检测事件的期望值以及在筛选步骤中获得的观察值。通过比较不同的安全边界,我们发现改进型的Chernoff界是Hoeffding不等式和乘法Chernoff界中最严格的一个。此外,我们还利用Azuma不等式对协议进行安全性分析,验证了在不稳定光子源强度波动下协议的可组合安全性。数值模拟结果显示,尤其是在数据相对较小的情况下,光子源的稳定性对于实际TF-QKD协议的性能至关重要。通过利用本文提出的协议可以为支持电力调度专用加密算法的电力专用量子加密一体机提供安全保障,从而给电力系统信息传输筑起了牢不可破的“金钟罩”,使电网再也不用担心外来攻击。
当然,本协议仍有一些不足可以改进。例如,本协议没有考虑量子信道中的噪声,但在实际环境中这是不可避免的,并且QKD安全成码的距离还远远达不到生活所需。接下来我们会针对这两个方面的问题对协议进行改善。
