类文丘里十字型流道中的液滴流态分析
2023-11-01夏侯彬蒋志韬陈忠利钱丽娟
夏侯彬,蒋志韬,陈忠利,钱丽娟,2
(1.中国计量大学 机电工程学院,浙江 杭州 310018;2.浙江省智能制造质量大数据溯源与应用重点实验室,浙江 杭州 310018)
微液滴以其尺寸小,可控性强,比表面积大等优点被广泛应用于生物医学[1]、药物筛选和输送[2]、食品工业[3]和化妆品制造[4]等行业。通常情况下,利用微流控技术生成微液滴主要依赖于多相流的流体流动,但同时也与所选择的微流道几何形状密切相关。这是由于改变微流道的几何形状可以有效地控制其内部多相流的流体动力学和界面演化过程,从而更好地制备所需特性的微液滴。
科研人员采用实验和数值模拟方法,就十字型流道结构变化对液滴生成的影响做了一系列研究。Liu和Zhang利用格子玻尔兹曼方法(lattice Boltzmann method, LBM)对十字型微流道进行了三维数值模拟,发现当微流道的宽深比以及两相进口的宽度比越大时,生成的液滴尺寸也就越大[5]。Gulati等通过实验探究得出十字交叉处的圆形结构会对液滴生成产生阻碍作用[6]。Zhang等利用水平集(level set method, LS)方法,比较了十字交叉型出口处4种不同颈缩结构下液滴生成的尺寸和周期,发现当出口颈缩结构为梯形时生成的液滴尺寸最小,频率最高[7]。Ngo和Iqbal等采用流体体积法(volume of fluid method,VOF)对十字流道进口夹角进行了研究,观测得出液滴尺寸在夹角为90°时最大,而随着进口夹角偏离90°,液滴尺寸会逐渐减小[8-9]。
综上所述,十字型流道结构变化的研究多集中在结构变化对于液滴尺寸和生成周期的影响。然而,对于流道结构变化下液滴流态的分析以及液滴生成时压力积聚现象并未有太多提及。查阅相关文献发现,文丘里结构可以有效缓解流道内的压力积聚问题,已有前人将文丘里结构加入T型流道中,来减缓液滴生成时的压力积聚问题[10]。因此,本文采用VOF方法,对类文丘里十字型流道的液滴生成流态进行分析,以便更好地理解液滴生成的机制,从而为后续实现液滴精确控制提供一定指导。
1 数值模型
1.1 控制方程
VOF界面追踪方法[11]利用体积函数α表示某一项流体在一个单元网格中所占体积分数。本文以分散相体积为主要研究对象,每个网格单元中两相流体的体积分数关系如下:
αd+αc=1。
(1)
式(1)中下标d和c分别代表分散相流体和连续相流体。
通过求解体积函数的输运方程来追踪两相界面,如式(2):
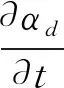
(2)
对于单元网格中的αd来说,若αd=1,则表示单元网格中全为分散相,若αd=0,则代表单元网格中全为连续相,若0<αd<1,则在单元网格中既有分散相又有连续相,即存在两相的交界面。
假设两相流体均为不可压缩的牛顿流体,其满足的连续性方程和动量方程如式(3)和式(4):
▽·U=0,
(3)

(4)
式(3)和(4)中:U是流体速度矢量,m/s;μ是流体动力粘度,Pa·s;ρ是流体密度,kg/m3;P是压力,Pa;g是重力加速度,m/s2;Fs是两相间的界面张力,N/m3。μ和ρ是流体的体积加权平均数,可以通过两相流体的体积分数表示,如下:
μ=μdαd+(1-αd)μc,
(5)
ρ=ρdαd+(1-αd)ρc。
(6)
Fs表示界面张力,可以通过式(7)的连续界面张力模型(continuum surface force,CSF)[12]计算得出
(7)
式(7)中,σ为表面张力系数,N/m;κ为界面曲率,可由式(8)计算得到
(8)
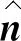
(9)
当相界面与通道内壁接触时,需要考虑壁面的粘附效应[13],它通常由壁面接触角决定,且接触角用于计算壁面附近的界面曲率,如式(10):
(10)
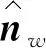
1.2 数值模拟模型
本文所用的十字型微流道的二维数值模拟模型如图1,两相入口宽度和长度均相等,通道宽度设置为Wc=Wd=100 μm,通道长度设置为Lc=Ld=100 μm。将交汇处改为类文丘里结构,其中缩进长度设置为Wv=Hv=25 μm,缩进角度设置为θ=45°。为了确保两相能够在主流道中充分流动,将主流道长度设置为Lmain=1 500 μm。分散相以流量Qd注入分散相入口,连续相以流量Qc注入对称的连续相入口。为简化计算成本,将连续相和分散相的物性参数设置为ρd=ρc=1 000 kg/m3、μd=0.001 Pa·s、μc=0.005 Pa·s,两相间界面张力系数设置为σ=0.01 N/m,接触角设置为θw=150°。

图1 十字型流道数值模拟结构示意图Figure 1 Schematic diagram of numerical simulation flow-focusing device
1.3 边界条件与数值方法
为了简化计算模型,对计算模型进行如下假设:两相流动均为不可压缩流动;与外界无热量交换;分散相与连续相在流动过程中无化学反应发生;两相流体的物性参数为常数。由于微流道流动中的雷诺数小于0.1,故选择层流模型和基于压力基的非稳态求解器。边界条件设置如下:两相入口都设置为恒定的速度入口,出口设置为压力出口,出口压力Pout=0 Pa。
使用VOF框架中的有限体积法求解控制方程以及压力隐式分裂算子(PISO)求解连续性方程和动量方程。压力方程采用PRESTIO!算法离散,而动量方程则通过二阶迎风格式离散。相界面重构采用分段线性界面法[14]。在全局库朗数小于0.2的标准下,采用变时间步长法确保计算的收敛和稳定。松弛因子设定如下:压力0.2,密度0.3,体积力0.3,动量0.2。
1.4 网格独立性验证
为了寻找合适的网格尺寸,本章采用结构化四边形网格对微流道的二维几何模型进行划分,网格划分如图2。选取三种不同网格数进行网格独立性验证,即32 400、41 560和64 750。定义两个形貌参数来进行独立性验证,分别是分散相的液线长度l和分散相的颈部宽度δ(见图1下方插图)。其中,颈部宽度在膨胀阶段定义为纵向最大宽度,在颈缩阶段定义为颈部的最小宽度。

图2 二维十字型流道网格示意图Figure 2 Schematic diagram of the grid of two-dimensional flow-focusing microchannels
图3(a)为膨胀和颈缩阶段下某一时刻的液滴形貌图。图3(b)为分散相液线长度随时间的演化过程。从图3可以看出,随着网格数的增加,数值模拟结果逐渐收敛。当网格数为41 560和64 750时,数值模拟结果趋于一致,考虑到计算和时间成本,故选用网格数为41 560的网格尺寸。

图3 不同网格数N=32 400、41 560和64 750下网格独立性检验结果Figure 3 Results of grid independence tests for different grid numbers N=32 400, 41 560 and 64 750
1.5 模型验证
为了验证模型的正确性,选取Soroor[15]所做实验进行对应的数值模拟。实验采用的十字型微流道的主通道宽度为125 μm交汇处出口的颈缩宽度为50 μm,长度为125 μm。选取甘油-水溶液(90%的水,10%的甘油)作为分散相(ρd=1 021.90 kg/m3,μd=1.16 mPa·s),矿物油作为连续相(ρc=830.66 kg/m3,μc=38.5 mPa·s),界面张力系数为σ=37.1 mN/m。数值模拟验证的实验条件为Qd=8 μL/min,Qc=7.62 μL/min。
数值模拟所得结果和实验对比情况如图4,左边为实验图,图中红色线条为采用LS方法所得的对照结果,右图为采用VOF方法所得的验证结果,从图4可以看出,尽管数值模拟中某些时刻液滴的轮廓存在差异,但整体曲率轮廓和文献中实验所得的曲率轮廓几乎吻合,故可以保证数值模型的正确性。

图4 数值模拟和实验所得的液滴生成过程的形貌演化对比图Figure 4 Morphological evolution of droplet generation process obtained from numerical simulation and experiment
2 流态分析
2.1 挤压态分析
数值模拟结果表明,挤压态出现在Ca较小且Q较大处。图5展示了挤压态在一个生成周期内相界面形貌、流场和压力场的非稳态演化。根据液滴生成过程中相界面的演化过程,将挤压态液滴生成过程分为4个阶段:膨胀阶段(expanding),挤压阶段(squeezing),颈缩阶段(necking)和断裂阶段(pinch-off)。
膨胀阶段(见图5,t=0~3.1 ms):从流线流动方向发现连续相大部分沿着交汇处的空隙流出,表明分散相受连续相的挤压作用较弱。随着交汇处分散相体积不断增大,连续相流出空间减小,造成交汇处压力积聚和升高。
挤压阶段(见图5,t=3.1~6.5 ms):连续相的挤压作用增强,分散相的径向宽度开始减小。分散相头部进入主流道,形成柱塞状。从流场变化可知,连续相的流线从交汇处的出口转向进口,流线的聚集程度减缓,使得交汇处的压力减小。
颈缩阶段(见图5,t=6.5~10.0 ms):分散相的颈部内凹变形并逐渐拉长变细,以抵抗连续相的挤压作用。连续相的流线垂直于分散性的流线,促进颈部的凹陷,使得颈部处的压力增大。
断裂阶段(见图5,t=10.0~11.5 ms):连续相流线的垂直分布表面连续相对颈部的挤压作用仍然存在,使得压力继续增大,促进颈部快速断裂形成液滴。在表明张力作用下,液滴尾部与断裂后的分散相前端后退回缩。
为了更好的理解液滴生成的机理,采用1.4节中定义的分散相的液线长度l和颈部宽度δ以及它们各自的变化率(Δl/Δt,Δδ/Δt)定量描述液滴生成过程中相界面的形貌演化。此外,将分散相头部前端界面内外的拉普拉斯压差(Δp=pi-po),见图5(a),t=0 ms,随时间的变化作为考察对象。从图5可以看出,在膨胀阶段,分散相头部在两相交汇处体积持续扩大,l和δ逐渐增大,见图6(a)(c),t=0~3.1 ms。该阶段内来自侧通道的连续相对交汇处的分散相的挤压作用增强,进而抑制了分散相头部在y方向上的膨胀,因此Δδ/Δt减小,见图6(d),t=0~3.1 ms。而这又促进了分散相头部向主流道下游的移动,使得Δl/Δt增大,见图6(b),t=0~3.1 ms。而后,当分散相头部到达两相交汇处出口后,由于流出空间的减小,分散相在y方向对连续相的挤压作用的抵抗增强,故Δl/Δt缓慢减小,见图6(b),t=0~3.1 ms,Δδ/Δt缓慢增大,见图6(d),t=0~3.1 ms。在膨胀阶段初期,分散相头部在惯性力的作用下不断膨胀,前端界面的曲率半径增大,Δp随之减小,见图6(e),t=0~3.1 ms,液滴稳定性增加,进而液滴前端界面趋向圆形。而在膨胀阶段后期,连续相的挤压作用加上流出空间的减小,使得分散相头部前端界面不断前凸,界面曲率半径减小,进而Δp增大,见图6(e),t=0~3.1 ms,液滴稳定性减弱,液滴前端界面偏离圆形。
在挤压阶段,随着连续相挤压作用的持续增强,交汇处内凸起的分散相受到挤压,δ开始缩小,Δδ/Δt变为负值且其绝对值随着时间持续增大,表明δ的减小速率不断上升,见图6(c)(d),t=3.1~6.5 ms。同时,l与Δl/Δt随时间明显增大,见图6(a)(b),t=3.1~6.5 ms,说明连续相的挤压作用还使得分散相头部向下游延伸。随着分散相从两相交汇处被挤入主通道下游的有限空间内,头部前端的曲率半径快速减小,Δp迅速增大,见图6(e),t=3.1~6.5 ms,液滴稳定性进一步减弱,液滴前端界面由圆形变为纺锤形。
从挤压阶段过渡到颈缩阶段时,两相交汇处被分散相完全堵塞,连续相的挤压作用达到最大,颈部开始内凹,Δδ/Δt达到最小,见图6(c),t=6.5~10.0 ms,并趋于稳定。而且,随着颈部收缩程度和分散相头部体积的增大,颈缩过程对l的促进作用大幅降低。因此,该阶段内,l随恒定流量的分散相的注入近似表现出线性增长,Δl/Δt小幅度的减小最后趋于稳定,见图6(a)(b),t=6.5~10.0 ms。随着主流道分散相头部的逐渐稳定,界面半径趋向稳定,Δp缓慢减小,见图6(e),t=6.5~10.0 ms,液滴前端界面又回到圆形。
在断裂阶段,颈部在Rayleigh-Plateau不稳定性[16]的诱导下断裂,δ减小到0,由于分散相对出流口的堵塞,Δδ/Δt并无较大变化,见图6(c)和(d)。由于断裂处颈部的体积很小,液滴颈部的夹断对分散相液线向下游移动的影响极其有限,因此,在该阶段内,分散相的液线长度延续了颈缩阶段结束时的变化率,即Δl/Δt和Δδ/Δt保持不变,见图6(b)。此外分散相头部前端的界面形貌已经达到稳定,故Δp基本不变,见图6(e),液滴前端界面保持圆形不变。
2.2 滴落态分析
在挤压态的基础上,减小流量比和毛细数,液滴生成流态转变为滴落态。滴落态下液滴相界面形貌、流场和压力场的非稳态演化如图7。与挤压态相同,滴落态中液滴生成也分为4个阶段。
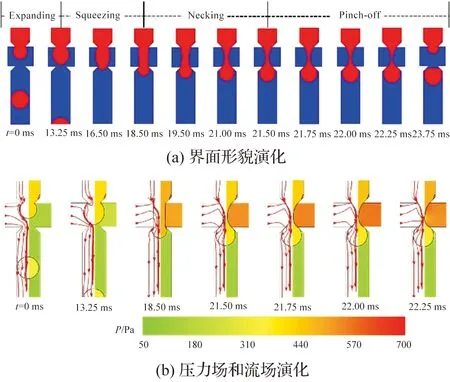
图7 滴落态液滴流体动力学行为的演化过程Figure 7 Evolution of the fluid dynamics behavior of dripping regime
膨胀阶段(见图7,t=0~13.25 ms):分散相的流量减小,交汇处分散相体积增大速率变慢,流线分布呈现出中间密两端疏的状态,两相交汇处的压力缓慢上升。
挤压阶段(见图7,t=13.25~18.50 ms):连续相粘性剪切作用下交汇处分散相开始收缩,主流道中分散相头部为圆形。连续相的流线从交汇处的出口转向进口,聚集程度减缓,交汇处的压力略微减小。
颈缩阶段(见图7,t=18.50~21.50 ms):颈部受到连续相粘性剪切作用开始内凹变薄,主流道内分散相体积缓慢增大。连续相流线垂直于颈部,流线汇聚使得压强升高。
断裂阶段(见图7,t=21.50~23.75 ms):在连续相粘性剪切作用下,流线汇聚位置相较于挤压态更靠近分散相入口,进而交汇处压强继续增大,促进颈部断裂形成液滴。
滴落态液滴界面演化特征参数如图8。在膨胀阶段,连续相的粘性剪切作用作为主导[17],l和δ平稳增加,Δl/Δt和Δδ/Δt保持不变,见图8(a)~(d),t=0~13.25 ms。此外,分散相头部前端的曲率半径缓慢增加,Δp缓慢减小,见图8(e),t=0~13.25 ms。
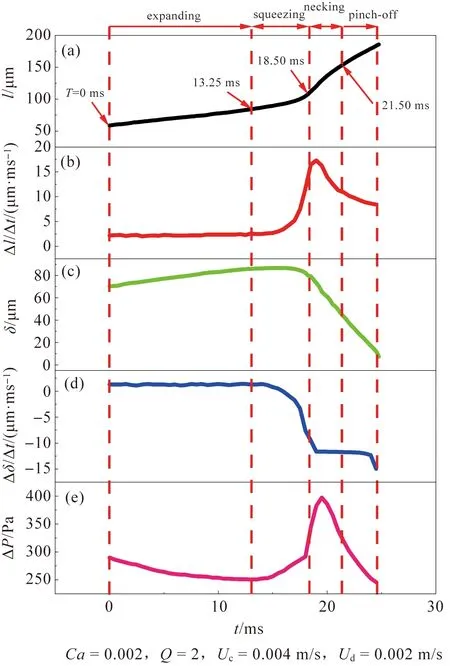
图8 滴落流态下液滴生成过程中特征参数演化Figure 8 Evolution of characteristic parameters during droplet generation in dripping regime
进入挤压阶段,连续相的粘性剪切作用持续,l和δ继续保持稳定增长,Δl/Δt和Δδ/Δt保持不变,见图8(a)~(d),t=13.25~18.50 ms。在挤压阶段后期,由于分散相头部体积的增大,使得连续相的粘性剪切与拖曳作用持续增强,进而引起颈部变细速率和头部伸长速率的加快,因此Δl/Δt和Δδ/Δt的绝对值随时间增大,见图8(b)和(d),t=13.25~18.50 ms。由于头部体积的增大,曲率半径开始减小,故Δp增大,见图8(e),t=13.25~18.50 ms。在颈缩阶段,分散相头部尺寸趋于稳定使得来自连续相的粘性剪切和拖曳作用的增强速率也随之降低并趋于稳定,进而引起Δl/Δt和Δδ/Δt的绝对值的增大逐渐变缓并趋于稳定,见图8(b)和(d),t=18.50~21.50 ms。分散相头部尺寸的增大,使得前端的曲率半径继续增大,进而Δp减小,见图8(e),t=18.50~21.50 ms。
断裂阶段,Rayleigh-Plateau不稳定性引起液滴颈部断裂,δ变为0,Δδ/Δt的绝对值急剧增大,见图8(c)和(d)。不同于挤压态,尽管液滴头部体积达到稳定,但此时分散相头部前端在界面张力的作用下逐渐变为球形,曲率半径不断增大,Δp继续减小,见图8(e)。
2.3 射流态流态分析
在挤压态的基础上,保持毛细数不变继续增大流量比,液滴流态转变为射流态。相较于挤压态和滴落态,射流态下并无液滴生成,而是形成一条均匀稳定的液线,随着两侧通道的连续相一起沿主流道流出,如图9。在射流态下,分散相的惯性力主导分散相液线的流动,且足够大的分散相惯性力可以抑制在两相交界处由界面张力诱发的Rayleigh-Plateau不稳定性,因此分散相与连续相界面处不会发生波动和破裂。
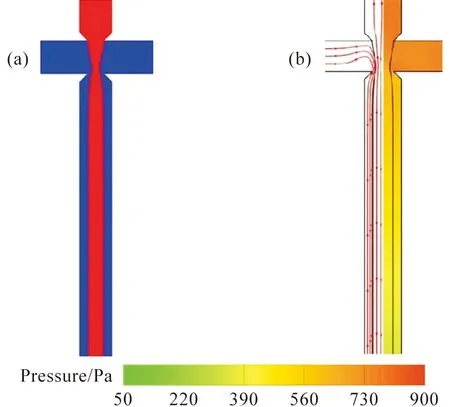
图9 射流态流体动力学行为的演化过程Figure 9 Evolution of the fluid dynamics behavior of threading regime
3 流态图分析
如上所述,毛细数和流量比的变化改变了液滴生成时不同力之间的竞争关系。因此,基于毛细数和流量比,绘制了流态分布图,如图10。当毛细数和流量比都较小时,连续相的粘性力和分散相的惯性力也很小,分散相在界面张力的主导下在两相交汇处经历膨胀和挤压过程,即出现滴落流态。随着流量比的增大,分散相的惯性力逐渐增大,促进了分散相液线的延长,同时使得分散相的颈部以及断裂位置向主流道下游方向移动,流态从滴落态向挤压态和射流态依次转变。随着毛细数的增大,意味着连续相对分散相的粘性剪切力增大,从而抑制两相间的界面张力作用,这有助于分散相液线向主流道的下游延伸。受此影响,流态转变所需的分散相惯性力减小,即流态转变的临界流量比随着毛细数的增大而减小。
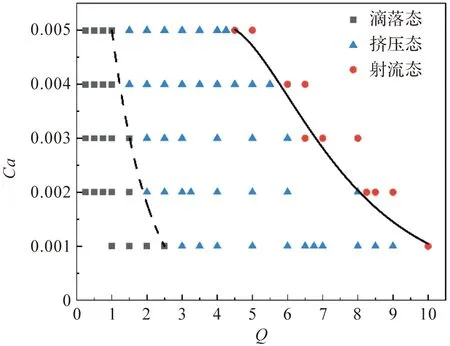
图10 流态转变图Figure 10 Flow regime transition diagram
针对流态转变图中的两条流态转变线条进行非线性的曲线拟合。得到流态转变的临界公式。滴落态与挤压态的临界关系如式(11),挤压态与射流态的临界关系如式(12):
Ca=0.01Q-1.45,
(11)
Ca=0.13Q-1.99。
(12)
从式(11)和(12)可以发现,挤压态向射流态转变的流量比的相关参数的绝对值要大于挤压态向滴落态的,这表明从挤压态向射流态转变所需的流量要大于挤压态向滴落态转变所需的流量。此外,当Ca增大时,流态转变所需的Q要减小。
4 结 语
本文在类文丘里十字型结构基础上,通过改变毛细数和流量比得到类文丘里十字型流道的3种典型流态。挤压态和滴落态的液滴形状分别为柱塞形和圆形。在液滴生成周期内,两种流态的分散相液线长度都随时间增大,颈部宽度都随时间先增大后减小。但由于两种流态下主导液滴生成的力不同,以及类文丘里结构的影响,使得液滴生成时作用力的竞争关系发生改变,造成形貌参数的变化率呈现出不同规律。挤压态下分散相液线长度变化率表现出波动上升最后趋于平稳,滴落态下分散相液线变化率趋势是先平稳不变再迅速上升最后缓慢减小。前者分散相颈部变化率大体表现为先下降后保持不变,后者分散相颈部变化率则是先保持平稳再迅速下降最后保持不变。射流态出现在流量比较大时,由于分散相惯性力足够大抑制界面张力而无液滴生成。同时,流态转变的流量比会随着毛细数的增大而减小,因此,为保证液滴能够以滴落态形式稳定生成,应适当保证流量比在0~1以内。
