基于CNN的电力数据分析模型研究
2023-11-01黄朝凯吴丹妍郑惠哲黄小奇
黄朝凯,吴丹妍,郑惠哲,黄小奇
(广东电网有限责任公司汕头供电局,广东 汕头 515041)
0 引言
随着网络、大数据、物联网、通信技术[1-3]的不断发展,智能电网可基于智能电表收集大量用电数据。因此,对这些海量数据进行分析,可推动电力系统服务质量的提升。然而,在电力供应过程中存在有意或无意攻击引起的异常用电行为,如非技术损失[4-5]的窃电行为。这种违法行为不仅严重扰乱了电力的正常使用,而且给电力系统造成了巨大的经济损失。同时,未经授权修改线路或仪表容易导致停电和火灾等事故,并对相关电力系统的安全构成严重威胁。
为此,大量学者对电力系统窃电检测方法进行研究,并取得了丰硕成果。文献[6]提出了基于遗传算法-反向传播(genetic algorithm- back propagation,GA-BP)神经网络的窃漏电用户识别方法,可实现电力系统实时运行数据记录和窃漏电用户识别。文献[7]提出了1种基于随机森林(random forest,RF)的电网用户窃电检测方法。文献[8]提出了基于时延细胞神经网络提取特征和支持向量机(support vector machine,SVM)的窃电检测方法。文献[9]基于差分整合移动平均自回归模型和递归贝叶斯(recursive Bayes,RB),构建了1种针对配电网低压窃电行为的识别方法。这些传统的数据挖掘方法易于实现,适用于小样本的窃电检测。
然而,这些方法特征提取能力低且检测精度有限。相对而言,深度神经网络不仅具有强大的特征提取能力,而且可以映射复杂的非线性关系。这使其相比传统方法具有更高的检测精度[10-11]。此外,窃电检测中另一个严重的问题是数据集中没有足够数量的窃电功率曲线。该问题为深度学习、SVM等监督学习方法带来了挑战。因此,有必要使用有限的窃电功率曲线进行数据增强,从而提高模型检测精度。
为改善上述问题,本文提出了1种基于卷积神经网络(convolutional neural network,CNN)的电力数据分析模型。首先,为了提高窃电检测的准确性,本文提出了1种基于条件变分自动编码器的窃电曲线数据增强方法。其次,本文设计了基于CNN的窃电检测分类模型。
1 基于条件变分自动编码器的数据增强
1.1 条件变分自动编码器
一般情况下,变分自动编码器主要根据历史数据X={x1,x2,…,xn}学习窃电功率曲线数据分布pθ(X)。窃电功率曲线数据分布可以分解为:
(1)
式中:n为历史数据个数。
为了简化计算过程,可对式(1)应用对数函数,获得如式(2)所示结果。
(2)
本文令功率曲线的每个数据点包含潜在变量z,则任意数据点x可以重构如下。
(3)
式中:pθ(z)为先验概率;pθ(x|z)为后验概率。
窃电功率曲线的生成过程通常包含以下步骤。
首先,根据pθ(z)获得潜在变量z;然后,根据pθ(x|z)生成窃电功率曲线pθ(x)。
然而,一般情况下pθ(z)以及pθ(x|z)无法获取。根据贝叶斯式,有:
(4)
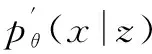
由于后验概率通常非常复杂,因此可基于1个简单的分布和参数φ近似估计后验概率。
为有效获取窃电功率曲线的分布,根据式(2),可先对log∏pθ(xi)进行估计。基于Kullback-Leibler散度与变分下界定义,有:
(5)


Eqφ(z|x)[-logqφ(z|x)+logpθ(x|z)]
(6)
本文将Kullback-Leibler散度用作对数似然的下界,则:
logpθ(x)≥L(θ,φ;x)
(7)
在这种情况下,L(θ,φ;x)可为:

Eqφ(z|x)[logpθ(x|z)]
(8)

基于上述条件,模型可以参数化为:
(9)
式中:f和g分别为具有1组参数的深度神经网络。


Eqφ(z|x){logpθ[(x|y)|z]}
(10)
1.2 数据增强过程
条件变分自动编码器的主要优点是不需要假设窃电功率曲线的概率分布,因此只需要少量样本即可训练模型,且可以生成与原始窃电功率曲线相似的样本。生成窃电功率曲线的执行流程如图1所示。
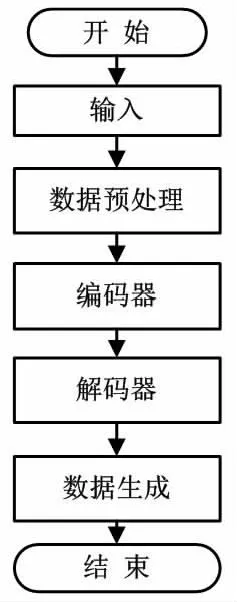
图1 生成窃电功率曲线的执行流程Fig.1 Execution process for generating power theft curves
根据图1,基于条件变分自动编码器的数据增强过程描述如下。
①在将数据输入条件变分自动编码器前,必须对窃电曲线的数据进行预处理,如归一化操作等。否则,训练的收敛速度将较慢,并且训练模型的性能将较差。因此,在保留数据的统计特征的同时,本文基于最小-最大重缩放变换将所有特征转换为固定范围[m,M]。对于给定的时间序列{xi},数据重缩放过程可表示为:
(11)

(12)
式中:xmax为时间序列{xi}的最大值。
②使用深度CNN构造编码器,将输入数据映射到低维潜在变量,计算编码器输出数据的均值和方差,用于生成相应的高斯噪声。所得高斯噪声为解码器的输入数据。
③将高斯噪声馈送到由深度转置CNN组成的解码器,从而生成新的窃电功率曲线。利用解码器的输出数据和实际数据计算损失函数。该损失函数用于通过反向传播方法更新编码器和解码器的权重。
④在训练条件变分自动编码器后,将高斯噪声馈送到解码器,以生成指定攻击模型下的窃电功率曲线。将生成的窃电功率曲线和来自训练集的原始样本进行融合,以形成增强数据集,并分别代入分类器进行训练,以实现窃电检测。
2 基于深度学习的窃电检测
2.1 窃电曲线分类
窃电功率曲线可分为4类,分别为一般窃电、拒绝攻击窃电、注入攻击窃电和交换攻击窃电。
一般窃电功率曲线低于正常功率,具体可表示为:
(13)

改装路由表、丢弃数据包和断开连接电表等攻击会导致拒绝服务。在这种情况下,电力表将停止报告消费者信息,即电力表数值为0。上述攻击下窃电功率曲线描述为:
(14)
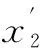
虚假信息攻击通过信息注入、特权访问、错误配置等手段生成虚假消费记录。注入攻击模型下,窃电功率曲线描述为:
(15)

此外,交换低电价时段和高电价时段之间的消费记录,也构成窃电行为。其窃电功率曲线描述为:
(16)

2.2 基于CNN的窃电检测模型
作为深度学习技术的代表算法之一,CNN以其强大的特征提取能力而广泛应用于图像分类、故障诊断和时间序列预测等领域。与传统分类方法相比,CNN不仅可以映射更复杂的非线性关系,而且具有良好的泛化能力。因此,本文选择CNN作为窃电检测的分类器。
2.2.1 模型结构
CNN由卷积层、池化层、展平层、全连接层等组成。具体而言,卷积层和池化层负责提取窃电功率曲线的特征。其数学式如下。
(17)
式中:xi为第i个卷积层的输入数据;yi为第i个卷积层的输出数据;y′为第i个最大池层的输出数据;fi为激活函数;bi和wi分别为第i个卷积层的偏移向量和权重。
为了缓解过度拟合,本文引入Dropout层以使某些神经元以一定的概率失去效能。同时,全连接层的数学式为:
(18)

考虑用电功率曲线的特点,本文提出的CNN结构如图2所示。

图2 CNN结构示意图Fig.2 Schematic diagram of CNN structure
图2中方块表示特征的维度,且每个特征大小已在方块上方说明。首先,为了便于训练,本文使用1×49维用电功率曲线将数据预处理为三维向量,并将其作为卷积层的输入数据。然后,本文使用2个卷积层和最大池层来提取功率曲线的关键特征。此外,2个卷积层中的卷积核数量分别为16和32。池化层后面接1个Dropout层,并令失效概率为0.25。最后,模型包括2个完全连接层,分别有15个和6个神经元。同时,模型中除最后一层使用softmax函数作为激活函数,其余层均使用ReLU函数作为激活函数。损失函数是分类交叉熵。优化器是Adadelta算法。
2.2.2 损失函数
一般情况下,网络训练时采用测量预测输出的绝对误差作为损失函数。具体描述如式(19)所示。
(19)
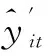
(20)
(21)
式中:α为调整权重的常数。
(22)
此外,对于第i个数据链,时间步t处的用电功率曲线可计算如下。
(23)
(24)
(25)
因此,缩放前的绝对误差计算如下。
(26)
在原始尺度上,不同样本的绝对误差具有不同的重要性。考虑到误差率为评估结果更常用的测量方法,本文进一步修正每个样本的损失。具体计算式如式(27)所示。
(27)
3 仿真与分析
3.1 数据集
为验证所提模型的有效性,本节基于中国某电网公司智能电表数据集进行模拟和分析。该数据集统计了中国某市2018年3月至2020年12月住宅及部分商业用户用电情况。功率曲线的采样周期设置为30 min。本文根据窃电曲线分类模型,随机选择一些样本生成窃电功率曲线,同时结合真实样本构成混合电力数据样本集。
上述数据集中窃电功率曲线样本均衡性较差,部分样本数量较低。为此,本文根据所提基于条件变分自动编码器的数据增强模型对窃电数据进行增强,从而进一步提高样本均衡性、加快模型训练速度及训练性能。数据增强后样本集数据统计情况如表1所示。

表1 数据增强后样本集数据统计情况Tab.1 Data statistics of sample set after data enhancement
3.2 仿真环境与参数设置
为保证相同试验条件,所有试验均运行在相同的环境。仿真环境具体如下:软件环境为由pycharm搭建算法框架,并由Python基于keras 2.2.4和tensorflow 1.12.0搭建CNN基础网络;硬件环境为酷睿i7 CPU、内存为128 GB ARM的联想服务器;操作系统为Ubuntu 18.04 64位,显卡为 NVIDIA RTX2080Ti 11G。
本文采用随机梯度下降(stochastic gradient descent,SGD)优化器训练模型。试验时,部分参数定义如下:批量大小设置为16;初始学习率设置为10-2;学习率衰减率设置为10-1;学习率衰减周期设置为10;最大迭代次数设置为150;每次迭代训练次数设置为100次。为消除试验过程因随机误差造成的影响,本文对不同模型分别执行30组试验,并取平均值作为测试结果。
3.3 性能分析
3.3.1 基础网络性能对比分析
首先,本节对比了所提模型与RF、SVM、RB、人工神经网络(artificial neural network,ANN)等模型的性能,从而验证所提模型的优势。试验时选取均方根误差(root mean square error,RMSE)指标来衡量模型性能。RMSE计算如式(28)所示。
(28)
式中:Pi为第i个样本的真实值;Oi为第i个样本的估计值。
RMSE较小表示模型估计能力较高,较大表示模型估计能力较低。不同模型比较结果如表2所示。
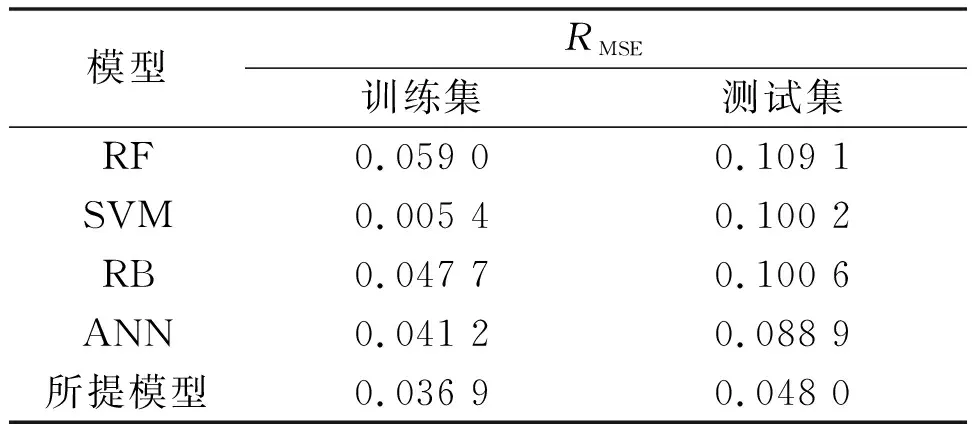
表2 不同模型比较结果Tab.2 Comparison results of different models
由表2可知,RF和SVM模型在测试数据上产生的RMSE通常比在训练数据上产生的RMSE高得多。这表明这些模型存在过度拟合问题。同时,RB和ANN等模型较RF和SVM模型性能有所提升,但RMSE仍有提升空间。所提模型性能优势明显,训练集中RMSE为3.69%,测试集中为4.80%。所提模型较RB和ANN在测试集中的RMSE分别下降5.26%和4.09%。
3.3.2 数据增强策略性能分析
为了验证所提模型生成窃电功率曲线的有效性,本节对比了基于随机过采样(random over-sampling,ROS)、人工少数类过采样技术(synthetic minority over-sampling technique,SMOTE)和生成对抗网络(generative adversarial network,GAN)等数据增强算法在所提基础CNN模型下的性能。对比指标分别选取准确率、F1分数和G均值。其中,指标G均值可有效评估不平衡样本性能。不同数据增强方法性能对比如表3所示。
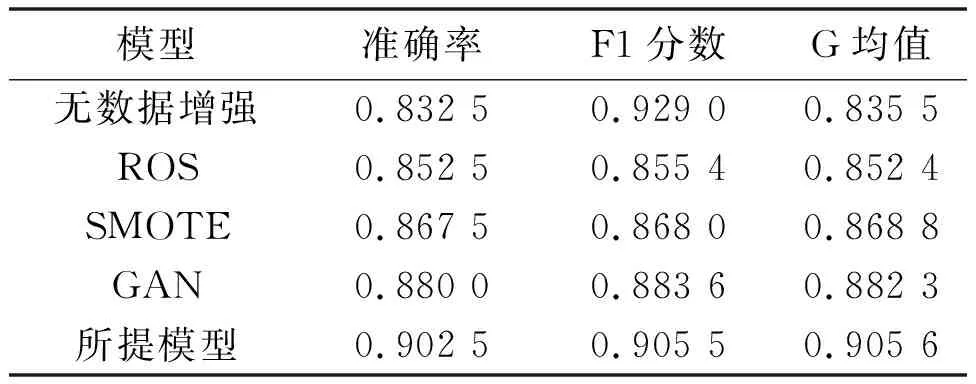
表3 不同数据增强方法性能对比Tab.3 Performance comparison of different data enhancement methods
由表3可知,通过不同方法增加数据后,基础CNN的检测性能得到了显著改善。具体而言,在通过ROS进行数据增强后,与原始数据集相比,CNN的准确率、F1分数和G均值分别提高了2.00%、1.64%和1.69%。经过SOMTE数据增强后,与原始数据集相比,CNN的准确率、F1分数和G均值分别提高了3.50%、2.90%和3.33%。经过GAN数据增强后,与原始数据集相比,CNN的准确率、F1分数和G均值分别提高了4.46%、4.46%和4.68%。经过无数据增强后,与原始数据集相比,CNN的准确率、F1分数和G均值分别提高了7.00%、6.65%和6.01%。因此,与现有的数据增强方法相比,所提数据增强方法可以根据窃电功率曲线的实际形状和分布特征扩展训练集,并且对CNN性能改善效果更优。
4 结论
本文对电力网电力数据进行了研究与分析,建立了1种基于CNN的电力数据分析模型。首先,本文基于条件变分自动编码器的数据增强,提高了样本的多样性和均衡性,提升了模型的准确性和训练效率。其次,本文提出了1种基于CNN的窃电检测模型,从而实现了用电数据的准确分类。该模型为电力数据分析及安全故障隐患的发现提供了借鉴。未来可对电力数据安全管理领域进行研究,如引入区块链、云计算等技术提高混合配电网数据交互可靠性及效率,以进一步完善智能化电力故障诊断及定位方案。
