车辆舒适停车二次速度曲线算法

徐哲,刘豪,党威,胡趁义,龙永文

(1. 重庆理工大学 车辆工程学院,重庆 400054;2. 东风柳州汽车有限公司,广西柳州 545000)

车辆的制动过程容易产生点头现象,引起驾乘人员的不适,有经验的驾驶员通过在制动后期松踏板可以实现对制动点头的抑制。随着电动制动助力器等关键零部件的应用,制动系统已经能够实现踏板与制动压力之间的解耦,通过在电动助力器中使用控制算法可以模拟经验丰富的驾驶员的松踏板操纵动作,实现车辆的舒适停车功能。另外随着自动驾驶时代的来临,车辆的制动操纵由驾驶员输入变为由控制系统给定,对制动过程的控制算法的好坏直接影响对车辆的评价,因此研究舒适停车控制算法具有重要的意义。

制动过程的舒适性优化可以由以下几个方面入手: 1) 单纯降低车辆俯仰角,可通过主动/半主动悬架产生主动力来控制车身在制动时的姿态[1-4],还可以通过调节前后轴制动力大小的分配来降低俯仰角从而优化制动舒适性[5-6]; 2) 从制动操纵输入进行控制,重新规划速度及加速度,在减小车身冲击度的同时减小制动俯仰变化程度[7]; 3) 将轮胎模型考虑到整车模型中,在制动后期,轮胎和车身由于制动钳的结合会引起整车的频率变化,使整车的振动频率下降到人体不舒适的频率范围内,故可以通过在制动后期调整制动力大小来使车身远离不舒适的频率范围,从而提高制动的舒适性[8-11]; 4) 通过微分平坦方法直接求解制动力,微分平坦是一种已知输出求输入的逆动力学方法,这种方法需要根据制动目标来对制动力输入进行逆向求解[12-13]。

通过主动(半主动)控制悬架各部件以此来控制车辆姿态的方法从理论上来说固然有效,但是由于其技术复杂加上成本昂贵,要想实现规模应用还有很长的路要走。调整前后轴制动力大小的分配来降低俯仰角在一定程度上解决了制动舒适性问题,但是其需要精确的识别路面条件来给制动力大小的分配提供有力的保障以确保行车的安全性。从频域上来解决制动舒适性往往会涉及到悬架与制动系统的联合控制,还是包含了通过悬架控制的缺点。

图1为解决制动舒适性常用研究方法的雷达图,可以看出每种方法都有一定的局限和优势,综合来说,通过制动力输入控制来改善制动舒适性具有较好的应用价值。

图1 制动舒适性研究方法雷达图

传统汽车的硬件结构决定了其制动力输入只能由驾驶员决定,而新型制动系统如电动制动助力器,可通过控制助力器内的电机主动调节制动液压力大小,从而使精确控制制动力输入成为可能[14-16]。在制动后期对制动力输入进行控制是目前解决制动舒适性问题的主流方法,许多厂商如博世、伯特利、联创所设计的产品功能的实现也是基于这一方法。

本文提出了一种舒适停车功能算法,通过重新规划速度及加速度曲线,在制动后期使速度呈二次曲线减小,加速度呈一次曲线减小,并使二者同时变为0,以此求解制动力输入,降低制动冲击度,提高制动舒适性。本文重新分析制动过程,指出停车制动速度变为零时的加速度阶跃变化时产生制动不适的主要原因,在此基础上设计控制算法,进行仿真,并考虑舒适性与安全性,完善舒适停车算法,开展实车试验。

1 制动不适原因分析

在制动过程中,随着时间的变化,车身及乘员通常呈现出不同的姿态,通过解构制动过程,可以分析出对制动舒适性影响最大的时期,才能有控制作用的侧重点,达到从机理上优化制动舒适性的目的。

根据车身及乘员的不同响应,可以将制动过程分为3个阶段[17]:制动前期,制动中期,制动后期。

图2为制动过程中车身与乘员的姿态变化示意图。

图2中垂直向上的箭头表示前后轴的载荷,水平箭头表示制动力,箭头的长短不同则大小不同。在制动初期,驾驶员踩下制动踏板,加速度开始建立,由于惯性作用,乘员开始前倾,且随着时间的推移向前倾的角度不断增大,此过程为车辆制动点头过程。直到制动中期,车辆加速度与乘员的惯性力在数值上保持稳定,此时乘员保持一种平衡状态,保持身体的前倾状态。到了制动后期,车辆速度为零,由于速度的消失,车辆的加速度也立即消失,此时车辆的加速度相当于阶跃输入,车辆的惯性力阶跃减小为零,乘员的俯身状态被打破,快速后仰。

图3为普通制动过程中的俯仰角和加速度变化曲线,在普通的制动过程中,即使车辆的加速度很小,其数值也会在制动后期突变为零,因为车辆完全停止时,与地面的相对运动也就随之消失了。加速度阶跃变化为零,这也是造成车辆停止后仰运动的原因。

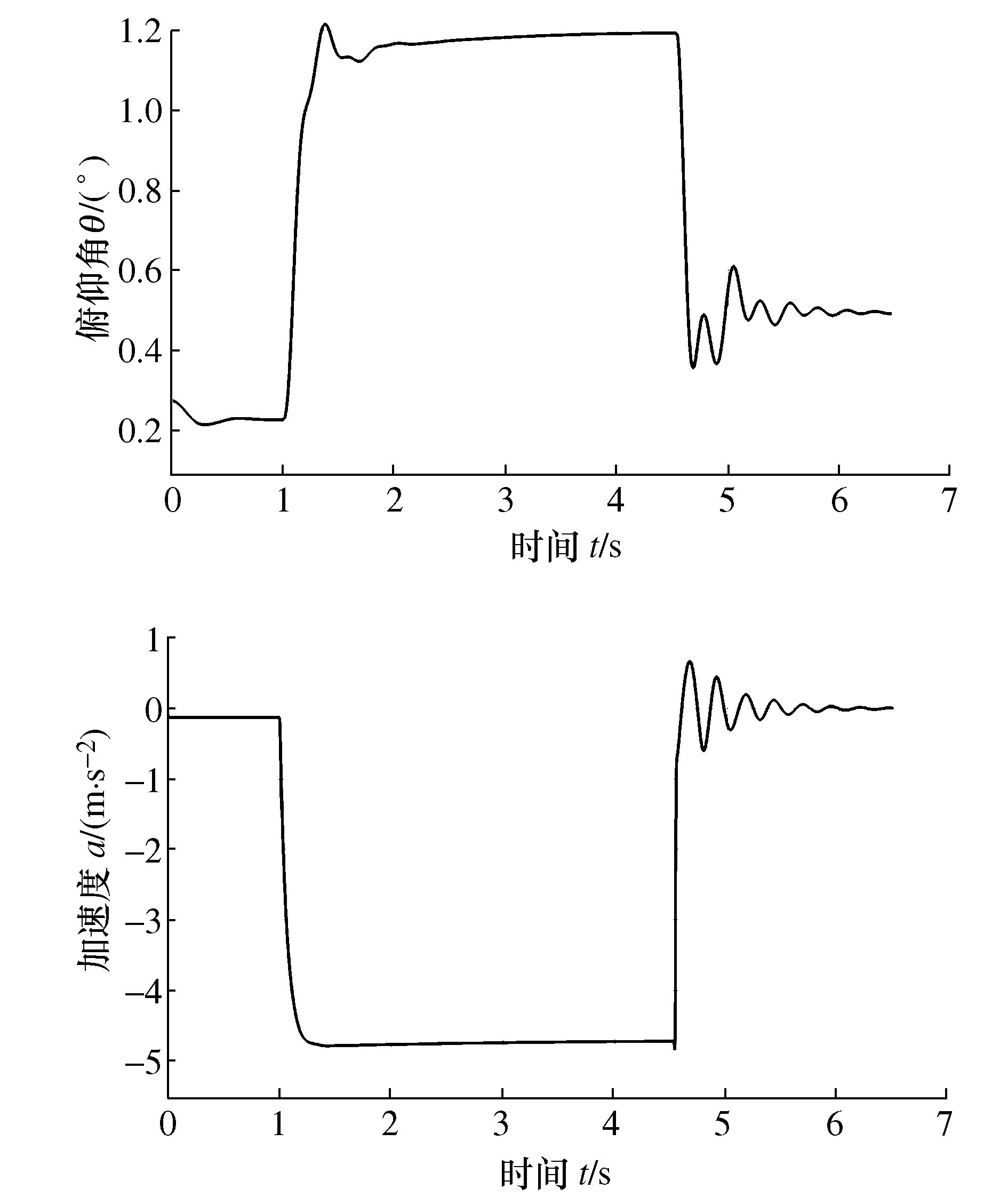
图3 普通制动时加速度、俯仰角曲线Fig.3 Acceleration and pitch angle response during normal braking

相关的研究表明[10],人们的前庭系统无法感受速度的变化,却能感受加速度的变化,制动后期姿态的变化极易使人晕车。所以制动舒适性的研究重心应放在制动后期上。由于在制动前期制动力的施加有个逐渐变化的过程,即使在紧急制动工况下,制动系统仍然需要100～200 ms的制动力施加时间,所以,该过程的加速度变化较为缓慢,所以其造成的不适较小。造成乘员不舒适的主要原因是在制动后期俯身状态的突然变化,这种突然变化可由冲击度大小来表示。本文以此为切入点,在制动后期通过重新规划速度曲线,减小冲击度优化制动舒适性。

2 控制算法设计

2.1 加速度规划

通过上节的分析可知,临近停车时应尽可能的使加速度处于较小的值,有研究表明,低于2.5 m/s2的车辆加速度对于乘客来说是舒适的。除了加速度的大小,加速度曲线对制动舒适性也很重要[18]。

控制加速度由阶跃形式减为0转变为在停止前缓慢减小并使车辆的瞬时加速度收敛于0是本文的目标。设计使加速度曲线连续的、小幅度的减小到0,即为一次曲线型的规划形式。

2.2 速度规划

在制动后期,加速度与速度曲线应平滑的收敛到0,以保证冲击度处于较小的值。图4为未进行规划时的速度曲线,呈一次曲线形式变化。

图4 普通制动时的速度曲线Fig.4 Velocity profile during normal braking

对制动后期的速度曲线进行规划,其算法原理可表示为:

ax(tf)=0,vx(ti)=0

(1)

ax(tf)=ax(ti)+j·(tf-ti)=0

(2)

vx(tf)=vx(ti)+ax(ti)·(tf-ti)+

(3)

(4)

式中:ax(tf)为算法结束后的加速度;ax(ti)为算法开始作用时的加速度;vx(tf)为最终的速度,vx(ti)为开始时的速度。

从式子的形式可以看出:式(1)决定了加速度的形式为一次型,式(2)决定了速度的形式为二次型,式(3)为冲击度的数值计算。冲击度作为评价舒适性的一个指标应为常数,其形式为

(5)

(6)

3 仿真验证

3.1 算法验证

完成舒适停车算法的设计后,在MATLAB环境下编写算法原型,得出了基于速度二次曲线规划的制动舒适性模型。假设初始加速度为-8 m/s2、舒适停车算法开始作用时速度为3 m/s,规划后的加速度、速度曲线如图5所示。

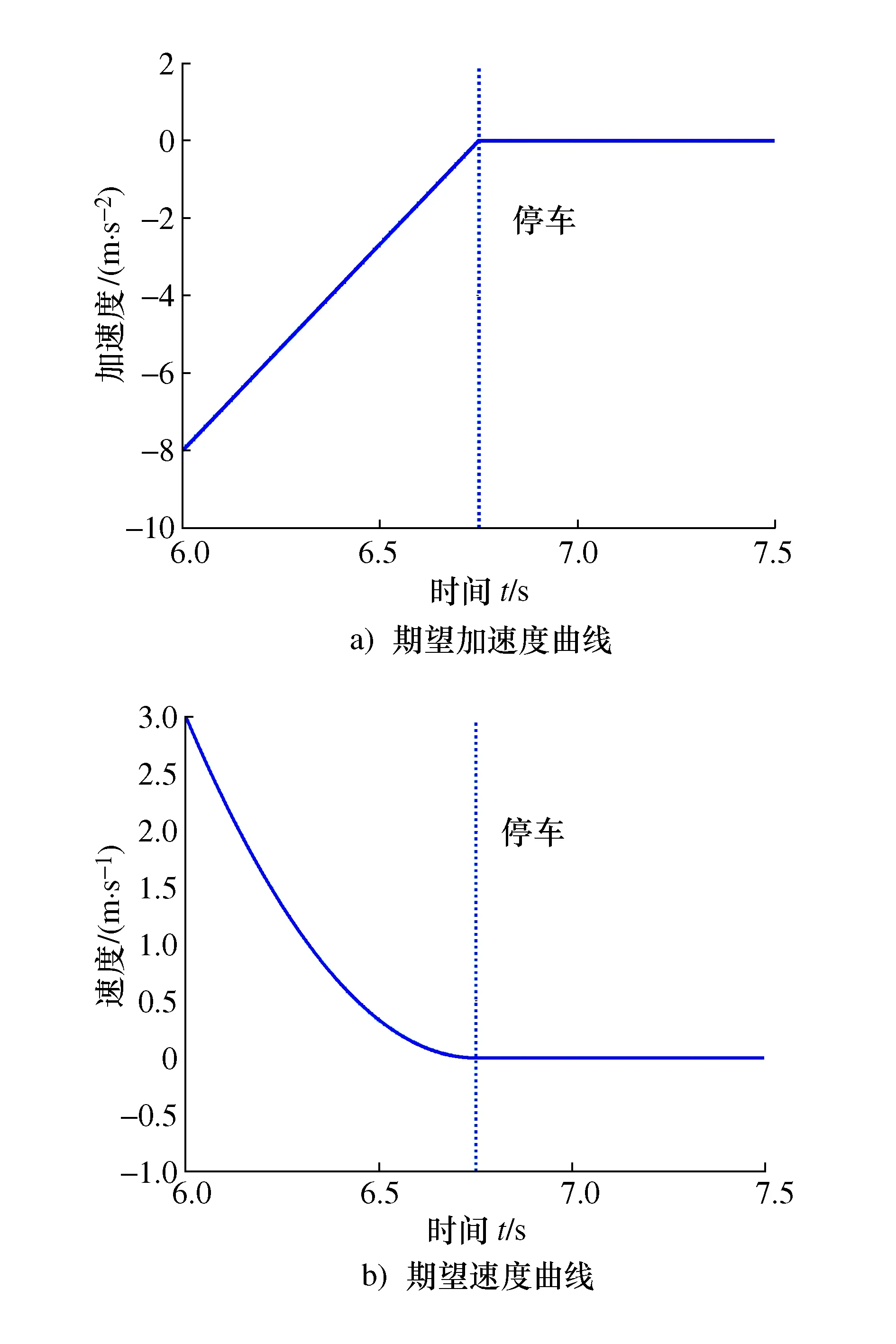
图5 规划的加速度、速度、冲击度曲线Fig.5 Planned acceleration, velocity and jerk curves

可以明显的看到,规划后的速度呈二次曲线减小,符合预期的设想。本文以制动时的冲击度作为舒适性评价的标准[19]。图6a)为普通制动时的冲击度曲线,在制动后期冲击度的数值很大,图6b)为理想的施加算法后的冲击度曲线。可以看到冲击度数值大大降低。

3.2 联合仿真验证

图7为舒适停车算法的整个控制框架,分为硬件和软件两个层面。可以看出算法的作用效果还需要在整车模型上进行验证。

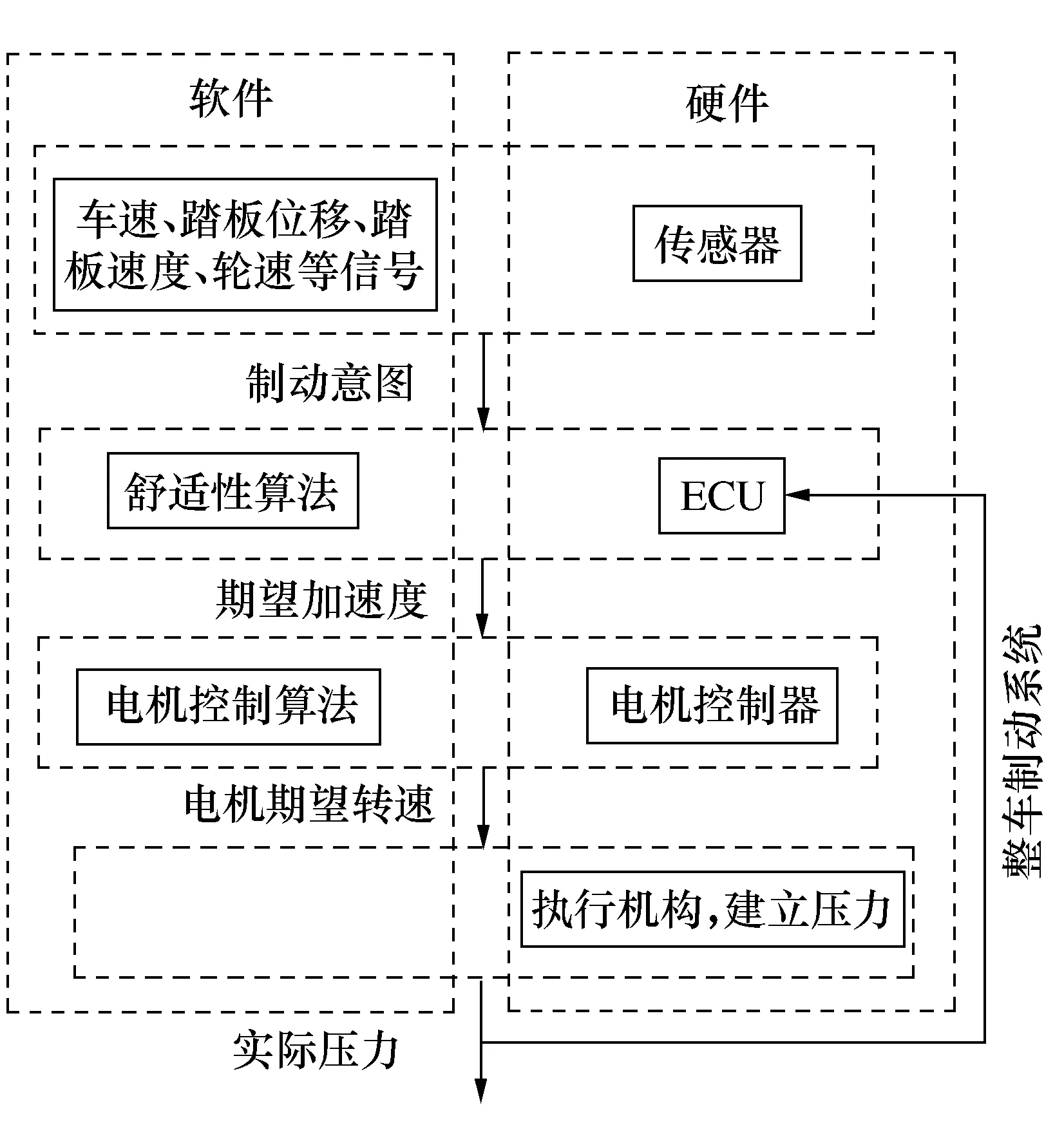
图7 舒适停车算法控制框架Fig.7 Control framework of comfort parking algorithm

在MATLAB/Simulink环境下搭建了舒适停车控制算法,与Carsim联合仿真,得到了带有整车模型的仿真结果,如图8所示。施加算法后速度呈二次型减小,加速度呈一次型减小,并且停车后的加速度波动幅度明显减小,在图8d)中可以看到,由于加速度的变化,在制动后期俯仰角也大幅度的减小,体现在冲击度上表现为很小的数值,制动舒适性得到了大幅度的提高。

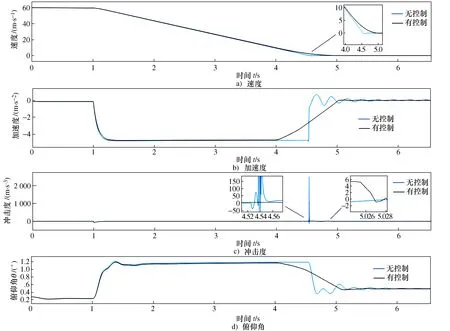
图8 理论上算法作用效果对比Fig.8 Comparison of theoretical algorithmic effects

4 舒适停车功能算法完善

在对制动后期的加速度、速度进行规划后,需要进一步完善算法,以保证制动的安全性。考虑到车辆处于制动工况,制动压力不能一直处于低压状态,不然会使驾驶员丢失制动信心而不被人们所接受,并且会降低车辆的安全性。基于以上分析,需要在减压后进行保压,之后再将制动压力恢复至原来水平,在这个过程中车辆也最终平稳的停下来。算法的作用还需考虑驾驶员的制动意图,在满足驾驶员制动意图下进行舒适停车算法作用,驾驶员意图可简单用踏板速度和踏板位移来描述,进一步可分为高强度制动,中强度制动,低强度制动[20]。在高强度制动时,以制动安全性为主要目标,舒适停车算法会主动退出。驾驶员制动意图不是本文讨论重点,故在本文中假设驾驶员以中低强度进行制动。

舒适停车需要界定工况发挥作用,通常在中小制动强度下工作,同时需要保证车轮不被抱死。舒适停车的过程实际是减小压力的过程,所以,减小压力实际上减弱了车轮抱死的可能性,另外车辆现在均配备了防抱死制动系统,当它监测到车轮存在抱死的可能时,控制器会作出决策,防抱死程序优先执行,舒适停车功能退出。

4.1 考虑因素

对算法进一步完善时,应考虑某些关键影响因素以保证算法的效果。针对算法的特点主要考虑以下4个因素:算法作用时的初速度、减压限值、保压时间以及增压速度。具体如下:

1) 算法作用时的初速度过高会导致制动距离延长,安全性降低,过低会导致算法的效果减小,舒适性降低。

2) 减压限值同样会影响算法的作用效果,若是压力释放的过多会使车辆处于不安全的工况,若是压力释放的过低,冲击度减小的不明显,制动舒适性仍未明显的改善,并且在控制过程中保持一定的制动管路压力能使车辆仍保持一定的制动能力,使得车辆在一定坡度的路面上不受影响。

3) 保压时间对应的是驾驶员的制动信心,若是保压时间过长,会让驾驶员产生“刹不住车”的感觉,保压时间过低仍会使冲击度过高。

4) 增压速度是指对制动系统再次建压的速度,若是此速度过高会造成车辆的二次冲击,仍会破坏制动舒适性。

4.2 改进后的仿真验证

图9是考虑了安全性的仿真验证。制动系统实时监测车辆状态,在车辆刹停前,当制动工况满足舒适停车算法作用的条件且车速降到3 m/s时,算法开始作用。速度曲线呈二次曲线形式,加速度曲线呈一次曲线形式且建压后的加速度震荡幅度减小,很快的收敛到0。从而俯仰角也迅速收敛到0,如图9d)所示,在制动中期,车身所保持的俯仰角也有一定的减小。对于冲击度而言,其数值大小从无控制的“2 511”减小为有控制的“125”,此“125”为制动系统增压至车辆完全停止时产生的冲击度。

图9 考虑安全性的仿真验证Fig.9 Simulation and verification with security considered

制动距离的长短可作为制动安全性的评判标准之一,图10为施加算法前后的制动距离对比,车辆的初速度为60 km/h,最大制动压力为3 MPa。如表1所示,未控制时的制动距离为46.24 m,施加算法后的制动距离为46.29 m,制动距离增加了5 cm,作为评价制动舒适性的冲击度却大大减小,改善的质量很可观。

图10 施加算法前后的制动距离Fig.10 Brake distance with or without algorithm implementation

4.3 实车验证

基于以上分析,重新优化制动舒适性算法并进行实车验证以验证算法的有效性。实验车辆为某国产电动汽车,该汽车的制动助力方式为电动助力,即利用电机对制动系统进行建压控制,可实现制动压力的精确控制。将Simulink模型编译成C代码,用编译器将代码刷写至电动制动助力器控制板上。当制动系统开始工作时,利用VECTOR VN1640A测试模块采集底盘数据,包括制动压力、制动加速度、车速等。并通过CANoe软件对数据信号进行和处理和分析,本试验按照《GB 21670-2008乘用车制动系统技术要求及试验方法》的标准进行。图11为实车及测试模块。

初始车速为40 km/h,在CANoe软件配置中选择显示制动压力、踏板行程、加速度、车速等参数。如图12所示,分别为制动过程中各参数的变化曲线,时间间隔T为保压时间,实验结果表明施加算法后,制动后期的加速度呈一次曲线减小,车速呈二次曲线减小,与仿真结果一致。且临近停车时加速度基本没有出现波动。车辆的制动冲击度在时域上被延迟并大幅减小,制动舒适性明显改善。

5 结论

本文对制动舒适性进行了深入的研究,重新解构了车辆制动过程,得出制动后期是影响车辆制动舒适性的关键时期的重要结论。提出了基于速度二次曲线规划的舒适停车算法,重新规划了速度曲线,通过仿真验证了算法的有效性,在抑制了车辆俯仰运动的同时减小了冲击度。考虑了制动舒适性与安全性的关系,改进控制算法,提出“减压-保压-增压”的解决方案,与Carsim联合仿真验证了改进后的控制策略,制动冲击度的数值从未优化的2 511降至优化后的125,制动舒适性得以改善。