典型山地风场三维效应大涡模拟研究
2023-10-30郑德乾卞莉李亮方平治
郑德乾,卞莉,李亮,方平治
(1 河南工业大学 土木工程学院,河南郑州 450001;2 中国气象局上海台风研究所,上海 200030)
0 引言
准确预测山区地形风场,对山区建筑物选址、建造至关重要。在大气边界层近地面处,受到地形起伏影响,空气流经山区形成复杂流动现象,使得山区风速预测更加困难。
目前对于山区地形风场的研究方法主要有理论研究[1-2]、风洞试验[3]和数值模拟[4]。随着计算机技术不断发展,数值模拟也越来越广泛应用于山区地形风场特性研究。基于时间平均RANS 方法(Reynolds averaged Navier-Stokes)和基于空间平均大涡模拟方法(large eddy simulation,LES)是较常用数值模拟方法。相较于RANS 方法,LES 方法不仅能够获得平均风场,也可以较为准确地获得湍流特性。Tamura 等[5]和Cao 等[6]采用大涡模拟和风洞试验方法,研究了不同来流情况下不同坡度粗糙与光滑表面二维山脊,研究表明大涡模拟能够很好模拟山区地形平均风场特性,但对陡峭山脊湍流特性,大涡模拟与风洞试验存在差异。Liu 等[7]对相同坡度二维对称山脊以及三维对称山丘进行风洞试验,研究不同维度下典型山地平均风和脉动风特性,研究表明受到三维绕流影响,三维山丘流动分离与二维山脊有明显差异。段静等[8]通过缩尺风洞试验,研究气流越过山体后背风面尾流分布特征。综上所述,大涡模拟在典型山地平均风特性方面有较好预测效果,对湍流特性尤其是山坡背风面存在一定问题需解决。且山地形横纵比对其三维效应如绕流撞击流动分离等现象影响需进一步明晰。
本文以典型山地为对象,采用基于自保持边界条件[9]改进涡方法[10-11]合成入流脉动,分别进行二维和三维模型非定常绕流大涡模拟,并与文献风洞试验结果对比,验证数值模拟方法有效性;从二维和三维模型风场演化、时均和瞬态流场及地形加速效应与各国规范对比,详细研究山地风场三维效应。
1 地形模型和CFD 模型
本文研究对象为图1 所示余弦型山丘[7],数学表达式为:
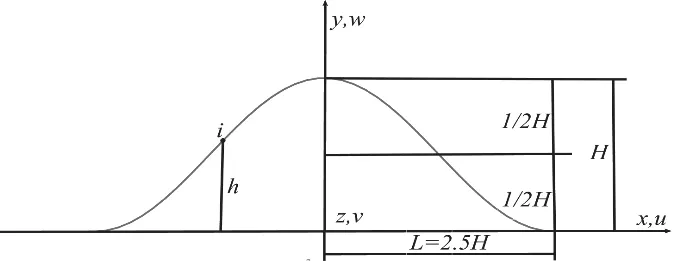
图1 山体形状
式中:H 为模型高度,取值为H=400mm;L 为迎风面宽度L=2.5H,其中山丘二维模型展向无限长。
本文二维山丘模型(下文简称“二维模型”)采用准三维计算,其中Mesh-1 和Mesh-2 计算域为37.5H(x)×10H(y)×10H(z),Mesh-3 计算域为37.5H(x)×12.5H(y)×22.5H(z),模型距离入流面12.5H,距离出流面20H,如图2 所示。采用非均匀结构化网格对计算域进行离散,在地面关心区域网格加密,具体设见表1。
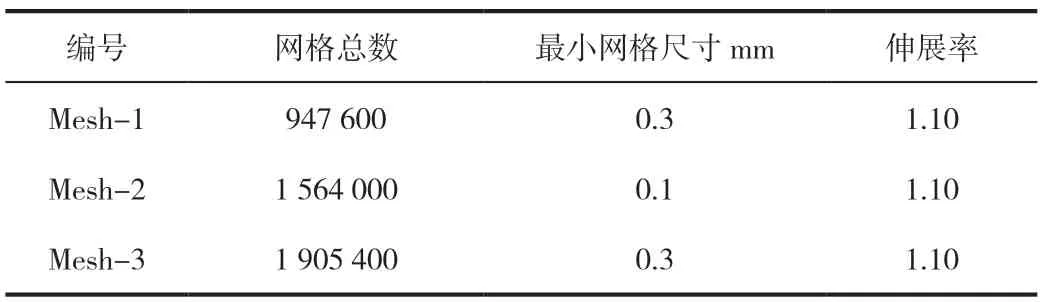
表1 网格分辨率
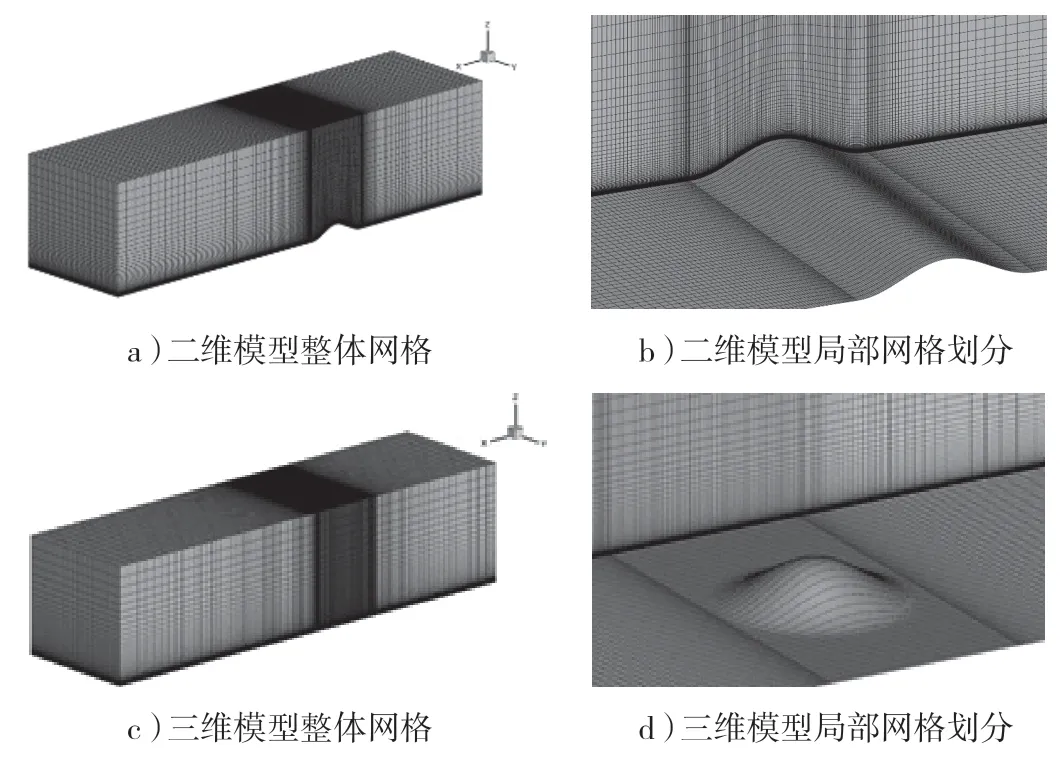
图2 计算域、计算模型及网格划分示意图
入流面为速度入口,入流脉动采用涡方法合成。出流面为压力出口,计算域两侧及顶部为对称边界条件,山体表面及地面设置为无滑移壁面。压力速度耦合采用SIMPLEC 算法;时间离散格式为二阶隐式,时间步长为0.0004s;空间离散格式采用有限中心差分格式,选用动态亚格子模型。
2 结果分析与讨论
平均风剖面和湍流剖面以模型上方4H 高度处风速Uref无量纲化[7]。地形加速效应是典型山地地形风场研究重要指标,其定义为[2]:
式中:Ui(x,z’)为z’高度处平均风速;U0(z’)为z’高度处来流平均风速;z’=z-h,其中z 为测点i 位置处距离水平地面高度,h 为测点i 位置处地形高度。
2.1 数值模拟方法可靠性验证
图3 为不同网格大涡模拟所得二维模型在入口处平均风及湍流剖面,图中“EXP”为文献[5]风洞试验结果,可知基于Mesh-1、3 网格模型得到湍流强度与风洞试验一致性更好,提高网格分辨率及扩大计算域未显著提高模拟精度,整体上与风洞试验差距较小,本文大涡模拟方法可有效重现B 类湍流边界层风场。
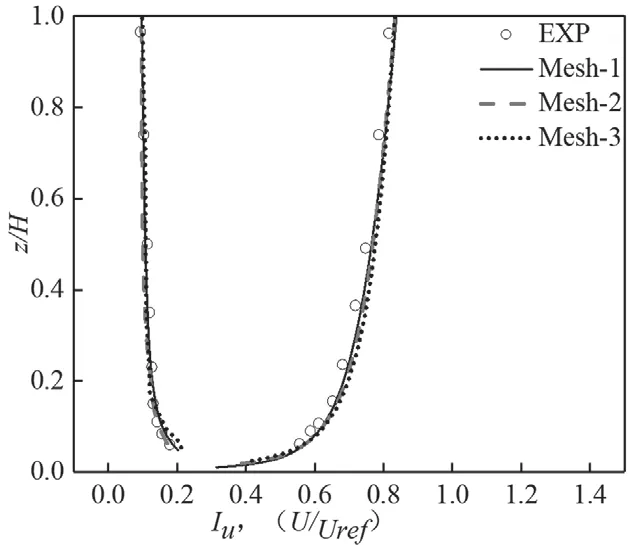
图3 湍流边界层风场大涡模拟与试验结果比较
图4 为不同网格分辨率二维模型y=0 纵剖面不同位置处平均和脉动风速剖面与风洞试验结果[7]和CDRFG 法[12]大涡模拟结果对比,由图可见:
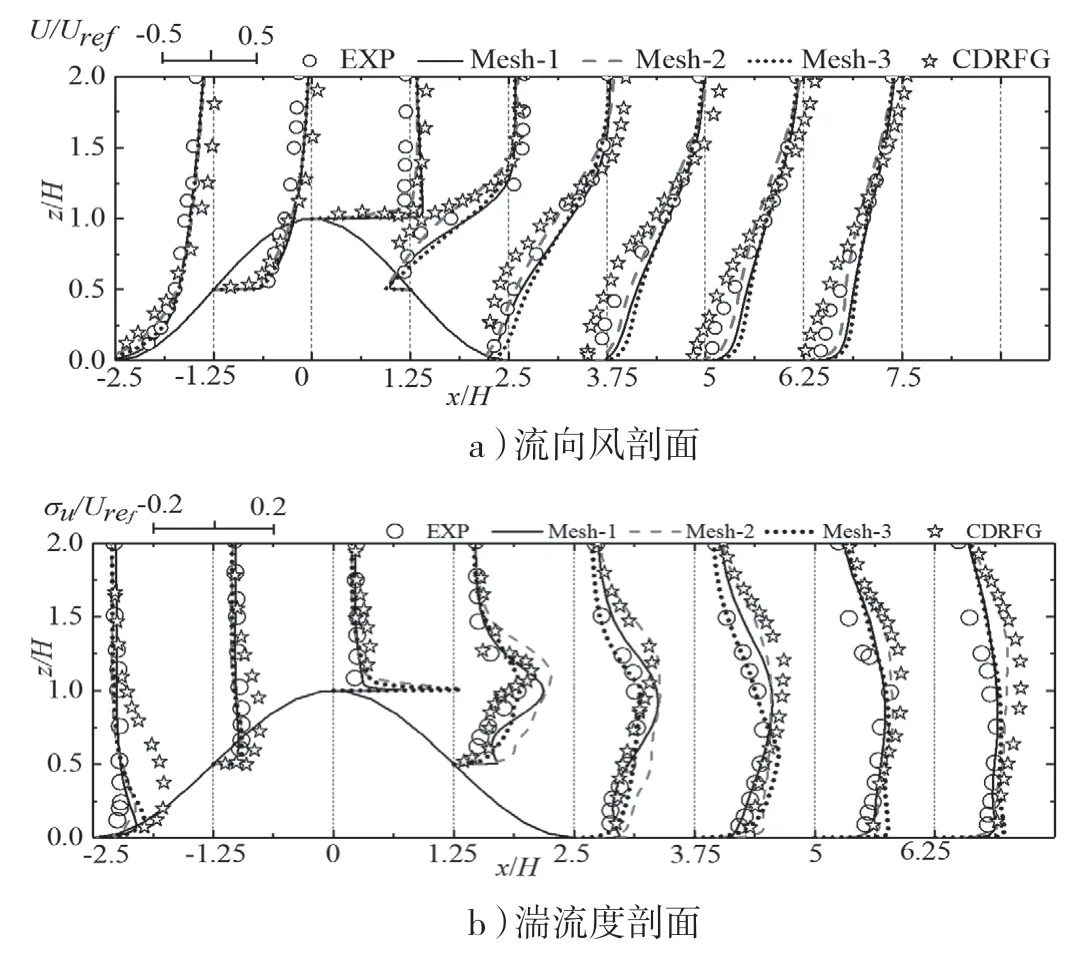
图4 二维模型风场大涡模拟与试验结果对比
1)迎风面,流向平均风(图4a)均随测点高度增加而增大,在山顶处近壁区达最大,数值比入流面近壁区相应位置增大5倍左右,说明受地形影响山顶处风速存在明显增大效应;在背风面,受到地形影响,背风面流向平均风剖面表现出流动分离更为剧烈,大致在x/H=0.91 位置开始发生流动分离且在近壁区有明显回流现象(图4a),在下游x/H=5 位置处逐渐恢复正常,这与文献[13]基本一致,本文大涡模拟方法是有效的;
2)湍流度剖面(图4b)总体迎风面近壁区随测点高度增加而减小,背风面尾流区明显观察到剖面形状在相当大高度范围内均存在较明显变形,值明显增大,由此说明受地形影响导致背风面湍流流动更复杂;
3)从不同网格模型模拟结果看,三种网格在二维山丘迎风面与风洞试验具有较好一致性,在模型背风面,扩大模型计算域能略微提高模拟精度,背风面三种网格与风洞试验趋势总体一致;提高网格精度未进一步提高湍流强度模拟精度,扩大模型计算域没有显著提高二维山丘模拟精度,由于计算域足够高,顶部对气流影响较小,风速在一定高度范围内变化较小,不影响背风面及尾流区气流分离和回流。综上,基于Mesh-1 网格模拟结果与风洞试验有较一致性;
4)对比CDRFG 法大涡模拟得到结果,对于平均风剖面(图4a)在迎风面至山顶处,两方法得到结果与风洞试验基本一致,主要差距在背风面尾流区,基于涡合成法大涡模拟在背风面过高估计近壁面风速,但其与风洞试验差距小于5%;湍流度剖面(图4b)CDRFG 法在迎风面山脚和山腰处过高估计湍流度,在背风面山脚和尾流一定高度范围内会过高估计湍流度,较涡方法与风洞试验差距较大。
由此可见,相较于CDRFG 方法需要复杂编程实现大涡模拟入流脉动生成,通过改变Fluent 内置涡合成法大涡模拟方法更高效、便捷及精度较高,后续计算均基于涡方法及Mesh-1 网格。
2.2 二维和三维山地模型风场比较
本节通过相同坡度二维和三维模型大涡模拟结果,分析地形风场三维效应,相应平均风剖面和湍流度剖面结果对比如图5所示,由图可见:
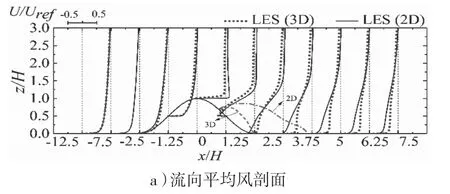
图5 二维对称山脊和三维对称山丘风剖面大涡模拟结果对比
1)对于流向平均风剖面(图5a),在模型前方和迎风面区域,二维模型和三维模型风剖面基本一致;在山顶处,二维模型流向地形加速效应明显大于三维模型,在z/H=1.01 高度处差距最明显,二维三维模型无量纲流向平均风速分别为U/Uref=1.04和0.01,说明受三维效应影响,三维模型在山顶处风速明显小于二维模型;在背风面及尾流区,二维模型流向平均风剖面变化更剧烈,在流动分离点位置,(红色虚线)三维模型分别约在x/H=0.76 位置处开始出现流动分离,约在x/H=2.5 位置处结束,而二维模型(绿色虚线),约在x/H=0.91 处开始出现流动分离,约在x/H=5 位置处结束,流动分离发生更早,位置更靠近上游,且水平影响范围较二维模型减小了约1.35 倍,下文流场分析中将予以解释。
2)对湍流剖面(图5b),在山顶位置近壁区,三维湍流度大于二维,分别在z/H=1.04 位置处差距最大,比二维模型分别大约1.64 倍;在x/H=5~7.5 位置处,差距明显,体现在z/H=2.0以下范围内二维模型湍流度不仅数值较大,且曲线拐点位置也高于三维模型,较三维模型平均高约22.2%。
2.3 二维和三维山地模型地形加速效应比较
地形加速效应是典型山地地形风场研究重要指标之一。本节将二维和三维模型计算所得迎风面山腰(x/H=-1.25)、山顶(x/H=0)和背风面山腰(x/H=1.25)三个位置处地形加速效应,与规范进行对比。
1)不同位置处三维与二维模型地形加速效应变化规律类似,均在近壁区达到最大。在迎风面山腰处(图6a),两种模型地形加速效应值相差不甚明显,自z/H=0.2 高度处开始出现一定差异,其中二维模型值略偏大,最大差值约5.8%。在山顶位置(图6b),两种模型差异显著,其中二维模型地形加速效应值总体上约为三维模型1.13 倍。在背风面山腰处(图6c),二者差异也比较明显,当z/H<0.5 时三维模型地形加速效应值偏大,而当z/H>0.5 时二维模型值偏大。
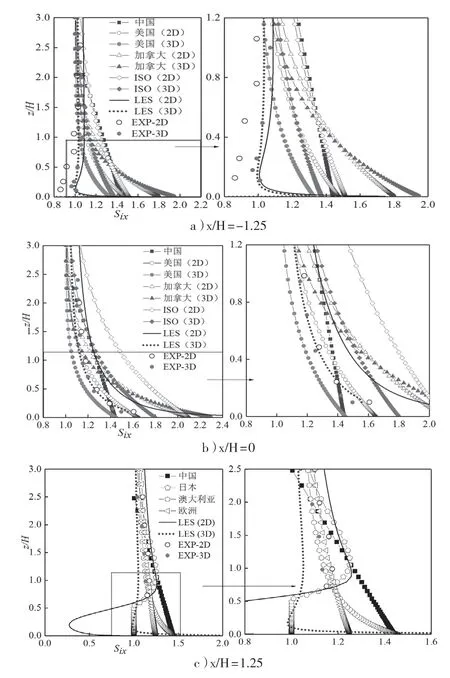
图6 地形加速效应对比
2)与文献实验[2]对比发现,大涡模拟得到二维山丘地形加速效应与文献实验相比,在迎风面和山顶处偏大,在背风面底部偏小,上部偏大,但总体与文献实验趋势一致;与二维山丘相比,大涡模拟得到三维山丘地形加速效应与风洞试验一致性最好,数值上比较接近,说明本文数值模拟方法有效性。
3)与不同国家规范相比,中国规范地形加速效应值随高度线性变化,其他国家规范和本文LES 结果均随高度呈现比较强非线性变化。在迎风面山腰位置(图6a)近地面处,LES 所得地形加速效应值随高度变化趋势比较剧烈,数值也明显低于各国规范值;就各国规范取值来说,中国规范取值介于各国规范中间,加拿大规范及ISO 规范地形加速效应偏安全。在山顶处(图6b),美国规范三维(“美国-3D”)地形建议值最小,ISO 规范二维(“ISO-2D”)地形建议值最大,本文数值模拟结果和其它规范值介于“美国-3D”和“ISO-2D”之间。对于背风面山腰位置(图6c)地形加速效应值,在z/H<0.5 近地面区域,本文三维模型大涡模拟(“LES-3D”)值Six≈ 1.0,与日本规范取值(该规范规定Six<1.0 时,取1.0)比较一致;而在z/H ≥ 0.5 位置,本文二维模型大涡模拟(“LES-2D”)结果与日本规范和中国规范建议值更为接近;澳大利亚规范和欧洲规范本文数值模拟、中国和日本规范建议值之间。
2.4 流场分析
图7 为不同时刻大涡模拟所得二维和三维模型流向y=0 纵剖面,以及三维模型距地z=1/2H 高度处水平截面瞬态涡量分布及其随时间演化。由图可见:
1)二维和三维模型迎风面前方近地面处均存在驻涡,其中二维模型前方驻涡尺寸相对较大,这是二维模型迎风面处气流仅能沿山体向上或向下流动,而三维模型则还能够沿山体两侧流动所致;随着时间增加,迎风面前方小尺度涡逐渐脱离并发展成为较大尺度条状涡;
2)在山顶,二维模型迎风面处形成旋涡逐渐脱离壁面并向山顶位置移动,在山顶处脱落,涡尺度均相对较大;相比之下,三维模型在山顶处漩涡脱落虽较复杂,但分离涡尺度相对较小,能量耗散更明显,这也是图5 中三维模型在山顶处湍流度剖面在近壁面变化较为复杂主要原因;
3)在背风面及尾流区,二维模型尾流区形成了上下覆盖范围较宽涡道,涡尺度较大;而三维模型尾流区涡道则相对较窄且更靠近上方,涡尺度相对较小,这是由于三维模型尾涡由山顶处脱落分离涡,以及山体两侧脱落旋涡(图7c)冲撞混合而成,导致旋涡脱落更为复杂,涡脱频率成分丰富,能量分布更分散,湍流强度相对较弱,存在较明显流动三维效应。
图8 为二维和三维模型在Q=1000 时模型周围瞬态涡量图,受地形影响,二维模型由于山体展向长度较长,气流在山丘表面仅存在“越山风效应”,漩涡只能沿山丘向上或向下演变,而三维模型不仅存在“越山风效应”,也伴随着“孤峰绕流”现象,漩涡绕山丘两侧绕流和向上演变影响,在背风面三维模型漩涡尺度更加丰富,条状涡和锥形涡、以及环状条形涡均存在,而二维模型则以条状涡为主,说明受到地形影响,山丘三维效应明显改变了模型在背风面涡结构;较三维模型而言,在背风面二维模型受到在山顶处气流流速较大影响,漩涡沿山体向下发展时,较三维模型会更远离壁面,这也是上文图5b 中在近壁面三维模型流向湍流度较大原因,同样,随漩涡在背风面不断发展,受到三维山丘影响,在背风面漩涡脱落和撞击现象产生更加频繁,且在周边有小尺度锥形涡以及条状涡脱离主涡道,而二维模型受到气流只能沿山体向上或向下限制,在背风面涡量演变多以大尺度条状涡和锥形涡为主,靠近山体背风面区域鲜有小尺度涡出现,说明受到山丘三维效应影响,可显著改变模型在背风面漩涡发展演变过程。
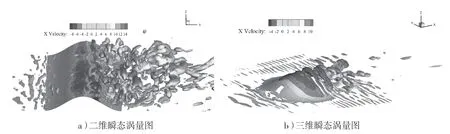
图8 二维和三维模型瞬态涡量图(Q=1000)
图9 为二维模型以及三维模型时均流线图,由图可见:受山体阻挡,气流在迎风面近地面处形成驻涡,同时气流发生绕流现象,分别沿三维模型两侧向后和迎风面向上绕流通过,而对于二维模型则仅沿迎风面向上绕流通过山体;在山顶位置均发生了流动分离,其中三维模型分离点较二维模型略靠近下游。以上流动现象不同,使得二维模型山顶处流向速度明显高于三维模型,这一点从图5a 所示流向平均风剖面对比结果可以更明显地观察到。在模型背风面,两模型背风面均形成了较明显分离泡,其中二维模型和三维模型分离涡核心距离地面分别为z/H=0.45 和0.75,二维模型为三维模型相应值0.6 倍,二维模型分离泡尺寸更大、更靠近地面,这是由于二维模型顶部气流速度较高所致。此外,由于三维模型分离涡较小且远离地面,使得其背风面近地面处还形成了一定流动再附现象。以上二维和三维模型流动特性不同,导致了两种模型在山顶附近、背风面及尾流区平均风剖面、湍流度剖面,以及地形加速效应值不同,可见,地形三维效应不容忽略。
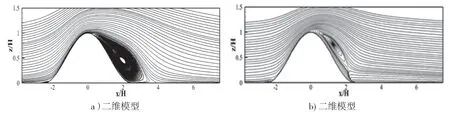
图9 流向y=0 纵剖面时均流线图
3 结论
1)本文基于涡方法大涡模拟方法及参数所得数值模拟结果与风洞试验具有较好一致性,能够有效模拟山地地形平均风以及脉动风特性,且满足湍流特性指标。
2)二维和三维山地模型平均风剖面和湍流度剖面在迎风面基本一致,但背风面流向平均风剖面和湍流度剖面存在一定差异,其中二维模型平均风剖面值较大,而三维模型湍流度剖面值较大,说明地形三维效应存在较明显影响。
3)流场分析结果显示,二维模型仅存在“越山风效应”,而三维模型不仅存在“越山风效应”,同时也伴随着“孤峰绕流”现象,因此其流场结构较为复杂,与二维模型相比,三维山地模型涡量分布以及漩涡脱落频率更复杂,能量更为分散,不同时刻三维模型尾流区漩涡脱落轨迹不尽相同,流动存在明显三维效应,这也是导致三维模型与二维模型背风面平均风和湍流特性均有较大差异的主要原因,因此在工程中,山脉等地形横纵比较小的地形可参考二维山丘模型,而山峰等横纵比较大地形因存在“孤峰绕流”等现象,需考虑地形三维效应。
4)二维和三维模型地形加速效应及其与各国规范对比表明,二维模型加速效应在迎风面和山顶位置偏大,而在背风面靠近地面处则明显偏小,地形三维效应不容忽略。不同国家规范地形加速效应取值总体上偏安全,特别是在近地面位置处;在迎风面和山顶处可参考加拿大规范和ISO 规范,而在背风面可参考日本规范。
