钢混组合梁结构受力分析与仿真试验研究

刘 洋

（中交公路规划设计院有限公司，宁夏 银川 750000）

随着我国路桥建设得到快速发展，为城市化进程贡献了突出力量，使出行更便利[1]。在路桥建设过程中，梁结构应用非常广泛。梁结构的质量直接决定了整个工程项目的品质，也对后续使用安全和使用效率起决定性因素。在传统梁结构的设计中，钢结构梁和混凝土结构梁是2 种非常常见的形式，都曾经在路桥建设中发挥了重要作用[2]。在此基础上，钢结构梁和混凝土结构梁在形式上融合，出现组合梁结构。同时，钢混组合梁使用混凝土材料和钢材，通过特定的结构设计和特殊的连接方式形成组合式的梁结构，发挥了2 种基本结构的优势[3]。因此，对钢混结构梁结构进行力学研究，并有针对性地分析2 种材料不同配置的钢混组合梁结构的性能，这对设计更合理的钢混梁结构具有十分重要的意义，这也是该文研究的出发点。

1 钢混组合梁结构的力学分析模型

钢混组合梁的结构设计是在钢结构和混凝土结构的基础上将2 种结构组合在一起，以达到更好的性能。在设计过程中，要根据工程项目的实际需求，对钢混材料进行几何结构层面的合理设计，进而通过调整相应参数达到最佳的设计效果。在该设计过程中依托钢混梁几何结构进行力学分析，是确保设计结果准确、可靠的关键。

1.1 截面换算分析方法

在截面分析和设计方法的实施过程中，将组合梁中的钢材和混凝土都假设为不发生塑性变形的弹性材料，那么这2 种材料组合以后仍然是弹性体。同时，忽略连接件的特殊属性，将其看作梁整体的一部分，并且也都符合弹性体特征。在这样的假设基础上，钢材和混凝土材料之间可能产生的滑移，也可以忽略不计。

从大量的工程项目实践中可以发现，钢混组合梁的力学特征和钢材为主体材料的梁结构更相似。因此，为准确地进行力学分析，可以将钢混组合梁的截面换算成钢材为主体材料的梁截面。换算关系如公式（1）所示。

式中：ACS为混凝土和钢材混合后形成组合梁的截面积；AC为混凝土结构梁的截面积；EC为混凝土结构梁的弹性模量；ES为钢结构梁的弹性模量。

经过截面换算后，组合梁结构中的混凝土截面都换算成了钢结构的截面，这样可以得到其几何特征，如公式（2）所示。

式中：ySC为组合梁结构完整截面的对称轴到组合梁截面底部的距离；yC为混凝土梁结构换算截面的对称轴到组合梁整体截面底部的距离；yS为钢结构梁换算截面的对称轴到组合梁整体截面底部的距离；ACS为混凝土和钢材混合后形成组合梁的截面积；AS为钢结构梁的截面积；A为混凝土材料换算后组合梁结构的整体截面积。

1.2 截面换算后的力学性能分析

经过截面换算后，梁结构中的混凝土部分需要达到的抗弯性能，如公式（3）所示。

式中：MC为组合梁结构中混凝土部分需要承载的弯矩；fC为合梁结构中混凝土部分能够提供的抗压强度；WC为组合梁结构中混凝土部分形成的抗弯截面系数。

经过截面换算后，梁结构中的钢材部分需要达到的抗弯性能，如公式（4）所示。

式中：MS为组合梁结构中钢材部分需要承载的弯矩；fS为合梁结构中钢材部分能够提供的抗压强度；Ws为组合梁结构中钢材部分形成的抗弯截面系数。

进一步可以计算组合梁结构中混凝土部分某一点需要承载的法向力，如公式（5）所示。

式中：σC为梁结构中混凝土部分某一点需要承载的法向力；M为组合梁需要承担的整体弯矩；yC为混凝土梁结构换算截面的对称轴到组合梁整体截面底部的距离；IC为组合梁结构中混凝土部分所能达到的惯性矩。

进一步可以计算组合梁结构中钢材部分某一点需要承载的法向力，如公式（6）所示。

式中：σS为梁结构中钢材部分某一点需要承载的法向力；M为组合梁需要承担的整体弯矩；yS为钢材梁结构换算截面的对称轴到组合梁整体截面底部的距离；IS为组合梁结构中钢材部分所能达到的惯性矩。

2 钢混组合梁结构的力学性能分析试验

在前文中，基于截面模型法进行钢混组合梁的力学特性分析，接下来将根据仿真试验对截面模型分析方法的效果进行检验。基于有限元模型构建钢混组合梁的三维仿真形态，如图1所示。

图1 钢混组合梁的仿真结构形态

图1 中，钢混组合梁是细小栅格构成的T 型梁结构，上方受到两处集中载荷的作用，可以考察钢混梁可能出现的受力和变形情况。

在仿真梁形态基本固定的情况下，对钢混组合梁的设计内容包括选择钢材的型号和混凝土。首先，以C50 型号的混凝土和Q355型的钢材为主要材料设计钢混结构梁。为便于细致地考察钢混结构梁可能出现的各种情况，进一步配置不同比例的钢纤维，包括4 种形式：第一种是以C50型号、Q355 型号钢材的混凝土为主要材料，不配置钢纤维。第二种是以C50 型号、Q355 型号钢材的混凝土为主要材料，配置0.5%的钢纤维。第三种是以C50 型号、Q355型号钢材的混凝土为主要材料，配置1.0%的钢纤维。第四种是以C50 型号、Q355 型号钢材的混凝土为主要材料，配置1.5%的钢纤维。

首先，比较当4 种材料可承受的极限载荷值和极限载荷发生时对应出现的挠度值，结果如图2所示。

图2 4 种型号钢材对应的极限载荷和对应跨度

从图2 的结果可以看出，4 种型号材料所承受的极限载荷都大于140kN，并且相差幅度不大。首先，从4 种型号材料可以承受的极限变形来看，以C50 型号、Q355 型号钢材的混凝土为主要材料并配置1.5%的钢纤维的材料效果最好，可以抵御约22mm 的变形；其次，以C50 型号、Q355 型号钢材的混凝土为主要材料并配置1.0%的钢纤维的材料，可以抵御约20mm 的变形；再次，以C50型号、Q355 型号钢材的混凝土为主要材料并配置0.5%的钢纤维的材料，可以抵御约18mm 的变形；最后，以C50型号、Q355 型号钢材的混凝土为主要材料并不配置钢纤维的材料，可以抵御约14mm 的变形。

进一步观察4 种材料配置的组合梁结构挠度变化随跨中距离远近的变化，如图3所示。

图3 组合梁结构的挠度变化随跨中距离远近的变化

图3 中，横坐标为测试点距离跨中的距离（X/L），纵坐标是跨中挠度，mm。从这组曲线的变化情况可以看出，4 种材料的最大挠度变化都发生在跨中位置。距离跨中两侧越远，挠度发生量就越小。从总体上看，以C50 型号、Q355 型号钢材的混凝土为主要材料并配置1.5%的钢纤维的材料，可以承受的挠度变化，一直优于其他3 种材料。

接下来进一步改变材料配置方式，在以T355 型号钢材为主要材料的基础上，改变混凝土型号的配置，分别配置C50 型号混凝土、C75 型号混凝土、C100 型号混凝土，从而形成3 种新的配置情况，进一步观察这3 种材料挠度的变化，结果如图4所示。

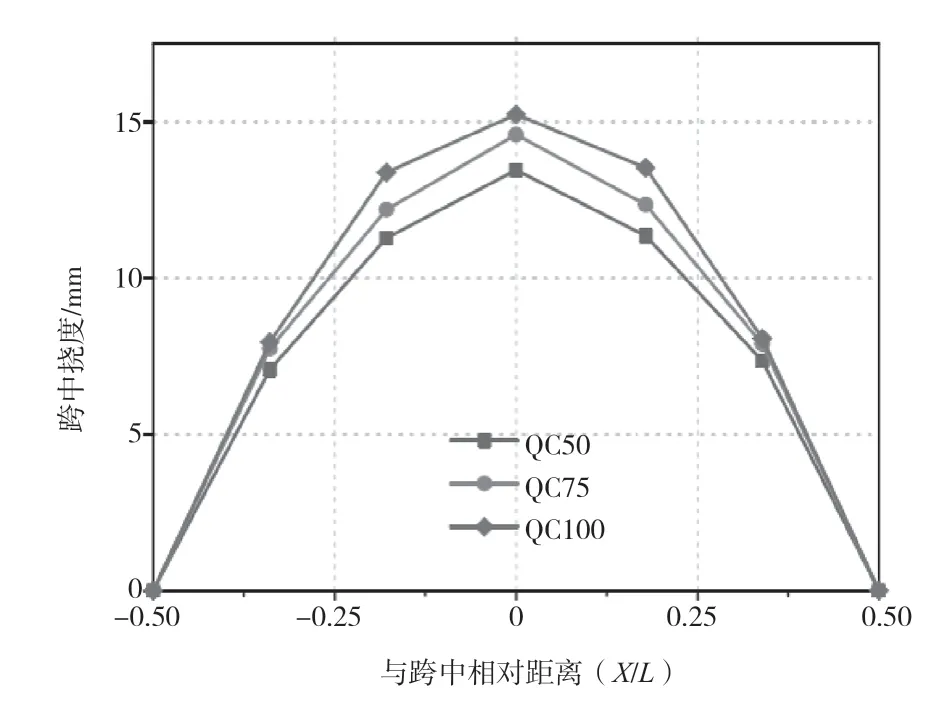
图4 另外3 种材料下组合梁结构的挠度变化随跨中距离远近的变化

图4 中，横坐标为测试点距离跨中的距离（X/L），纵坐标是跨中挠度，mm。3 组曲线中，QC50 代表以C50 型号混凝土、T355 型号钢材的为主要材料的组合梁，QC75代表以C75 型号混凝土、T355 型号钢材的为主要材料的组合梁，QC100 代表以C100 型号混凝土、T355 型号钢材的为主要材料的组合梁。

图4 中3 种材料的最大挠度变化都发生在跨中位置。距离跨中两侧越远，挠度发生量就越小。3 种材料的组合梁的挠度变化曲线都比较接近，跨中挠度极限值分布在13mm～15mm，差距不大。综合图3 和图4 可以看出，新配置的3 种材料，对最大变形的承受性能，要弱于之前的4 种材料。由此可以看出，组合梁中钢纤维植入的必要性，可以更大程度地提升钢混组合梁的性能。该结果也可以表明，为了提升钢混组合梁结构的力学性能，除了混凝土和钢筋的合理配置，还要注意钢纤维的植入，进一步提升梁结构的抗弯性能，从而提升其在载荷情况下抵抗变形的能力。

3 结论

在混凝土结构梁和钢结构梁基础上发展起来的组合梁，对路桥工程具有十分重要的意义，其安全性更高、使用范围更广。该文依托截面模型分析法，首先，将混凝土材料进行钢材料的截面换算，进而构建包括截面、挠度、弯矩和抗弯效果等参数的力学分析模型。其次，分别设计7 种材料组合下的混合梁结构，并分析其所能承受的极限载荷值和所能抵抗的最大挠度变形情况。试验结果表明，组合梁跨中挠度最大，距离跨中越远，产生的挠度变形越小；从7 种材料的配置情况来看，以C50 型号、Q355 型号钢材的混凝土为主要材料并配置1.5%的钢纤维的材料可以达到最好的力学性能效果，这也证明钢纤维植入对钢混组合梁具有十分重要的作用。