水轮发电机组碰摩转子系统模型的周期解及数值分析

刁洋洋

（山东华邦建设集团有限公司，山东 潍坊 262500）

水轮发电机组的转子和定子之间具有一定的轴径间隙，受振荡作用的影响，转子在水平方向存在小幅度的偏移风险，进而导致定子和转子间出现碰摩，探索碰摩转子系统的周期解能够建立科学的运动控制参数、降低碰摩对转子和定子的破坏程度。由于运动过程属于强非线性微分方程，难以直接求解，因此运用数值分析法进行迭代计算。

1 水轮发电机组碰摩转子系统模型及运动方程

1.1 转子-轴承模型

在直角坐标系o-xyz中，水轮发电机组的定子和转子运动系统如图1所示，其中椭圆实线部分为发电机定子，椭圆虚线部分表示发电机转子，定子和转子的几何中心为o点，轴径的初始中心为s点。当系统处于静止状态时，o点和s点重合；当系统处于运动状态时，受振动效应的影响，o点和s点有可能出现位置偏移。A点和B点分别为上导轴承、下导轴承的几何中心，ω为大轴转速。将转子的重心记为G，转子的质量偏心可为向量e0，大轴的旋转偏心可为向量e。

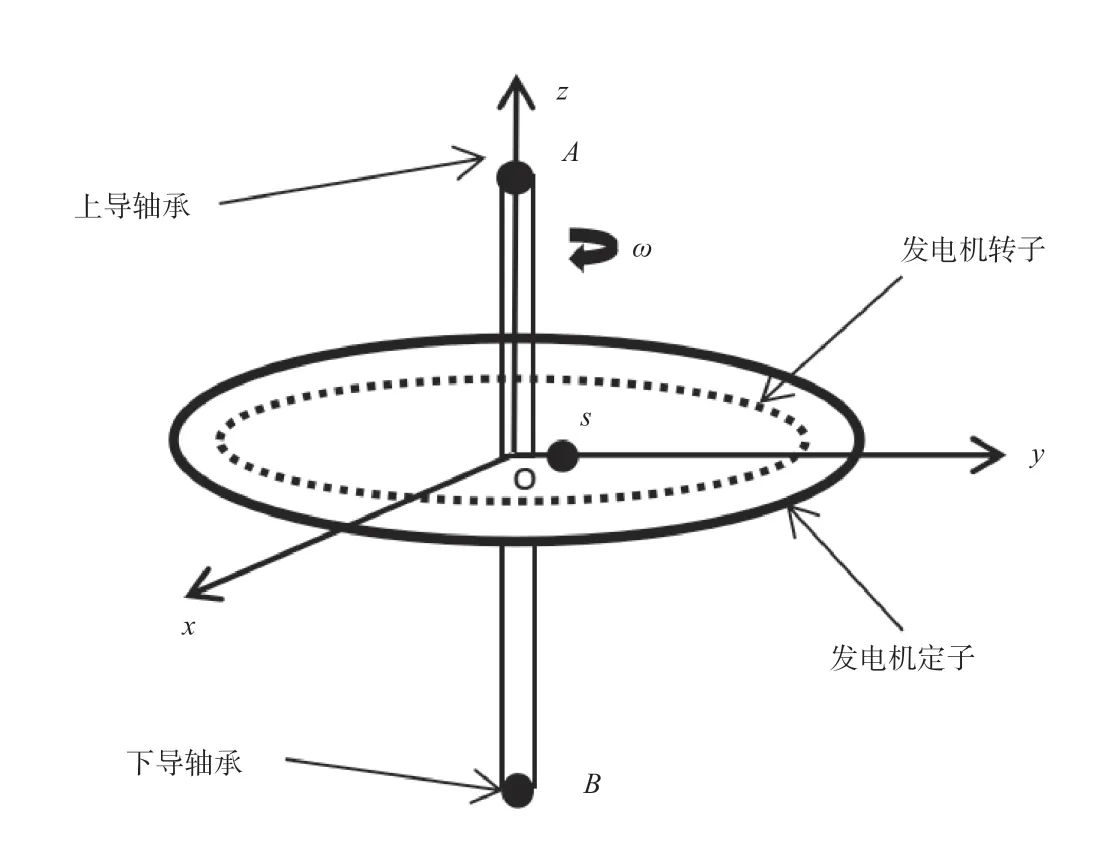
图1 水轮发电机转子-轴承系统示意图

1.2 建立运动微分方程

1.2.1 模型基本假设

将发电机转子简化成质量为m1的圆盘结构，转子的支撑结构为可滑动的轴承，该轴承为均匀的对称结构，其上、下端质量均为m2。转子位于上、下导轴承的中点，以线性方式处理轴承的阻尼和刚度。转子的振动效应较复杂，存在多个方向的分量，该模型仅考虑横向振动，不考虑陀螺力矩和扭转效应的影响。

1.2.2 转子-轴承碰摩运动微分方程

在仅考虑横向振动的情况下，转子在水平方向会产生一定的振动幅值，转子和定子之间存在特定的距离，当转子的水平运动幅值超过该距离时，转子和定子就会产生碰摩作用。从理论上讲，碰摩过程必然会引发热效应，并且定子会发生不可预知的形变[1]。为了便于建立运动微分方程，可将定子形变视为线性形变，同时不考虑碰摩产生的热效应。综合以上假设条件，定子和转子之间的摩擦力符合库仑摩擦力（见表1）的应用条件。转子处于运动状态，当产生碰摩作用时，以滑动摩擦力为主，将摩擦力分解至x轴和y轴，分解后的摩擦力如公式（1）所示。

表1 库仑摩擦力的基本观点

式中：Fx_rub、Fy_rub为撞摩擦力在x、y轴的分量；e1为发电机转子的径向位移；f为摩擦力系数；kr为定子径向刚度；δ0为定子和转子的平均气隙长度；H为函数。

H函数式如公式（2）所示。

根据现有研究成果，水轮机转子-轴承系统在运行过程中主要存在3 种作用力，分别为不平衡磁拉力（Unbalanced Magnetic Pull，UMP）、碰摩力和非线性油膜力。将轴承径处的坐标记为（Z，W），则定子-转子系统的运动微分方程组如公式（3）所示。

式中：m1为电机转子圆盘的质量；m2为轴承上端或者下端所集中的质量；转子质量偏心为e0；c1为转子处的阻尼；c2为轴承处的阻尼；Fx_ump、Fy_ump是不平衡磁拉力在x轴、y轴方向的分量；Ke为大轴的刚度；fx、fy为非线性油膜力在x轴、y轴的分量；将转子外圆几何中心的坐标记为（X，Y，0）；X''、X'分别为对坐标的二阶微分、一阶微分；Y''、Y'、Z''、Z'、W''、W'的含义与X''、X'类似。

2 碰摩转子系统模型的周期解及数值分析

2.1 周期解的近似表达式

2.1.1 运动微分方程的解析方法

谐波平衡法（Harmonic Balance，HB）是处理非线性问题的常用方法，但公式（3）属于强非线性微分方程，HB 方法难以对该方程进行解析[2]。隐式谐波平衡法（HB-AFT）由HB 方法和时域频域转换技术（Alternating Frequency/time，AFT）综合发展而来，能够解析强非线性微分方程，其原理如下。

假设存在某个非线性系统，其二阶微分方程如公式（4）所示。

为了得到公式（4）的周期解，假设x与t的关系式为x（t），并且x（t）为周期性函数，其周期为T，于是有x（t）=x（t+T）。此时函数f（·）与x（t）建立了相同的正交基，可分别对其实施傅里叶展开，进而获得二者的隐式非线性代数关系式。

2.1.2 周期解近似表达式的推导过程

根据HB-AFT 方法的应用原理，应该先对公式（3）进行非线性函数谐波平衡化，再从中获取主方程，具体过程如下：对方程在X、Y、Z、W这4 个坐标点的周期解实施傅里叶展开，得到相应的傅里叶级数形式和线性外力的傅里叶级数[3]。例如非线性外力如公式（5）所示。式中：cx0、cy0、cz0以及cw0均为常数；cxk、cyk、czk以及cwk为余弦项相关的系数；dxk、dzk、dwk以及dyk为正弦项相关系数。

将经过傅里叶展开的周期解和非线性外力代入公式（3）中，即可推导出有关常数项的代数方程，将该方程记为G。将X、Y、Z、W方向的周期解经过傅里叶展开后同样可得到常数项ax0、ay0、az0、aw0，相应的余弦项系数为awk、azk、ayk、axk，相应的正弦项系数包括bwk、bzk、byk以及bxk。

难以直接对隐式非线性方程G进行求解，于是利用牛顿迭代法来求解，其实施步骤包括确定需要迭代的变量、构造迭代关系式以及控制迭代过程[4]。利用X、Y、Z、W方向周期解傅里叶展开级数中的常数项、余弦系数项、正弦系数项，构造出迭代关系式P，则有P=[ax0ay0az0aw0ax1ay1az1aw1bx1by1bz1bw1...axkaykazkawkbxkbykbzkbwk]。再将非线性外力经过傅里叶展开所形成的常数项、正弦系数项、余弦系数项构建立为迭代式Q，则有Q=[cx0cy0cz0c w0cx1cy1cz1cw1dx1dy1dz1dw1...cxkcykczkcwkdxkdykdzkdwk]。在求周期解的过程中，将迭代关系式Q作为已知因素，P为求解目标，以不动点迭代法求解P，但计算过程涉及大量数学推导且较抽象，难以直观展示，下文将通过数值分析展示求解过程。

2.2 数值分析

以某型水轮发电机为数值分析对象，其对应的m1、m2质量分别为60kg、25kg，转子阻尼和轴承阻尼分别为c1=4000N·s/m、c2=1200N·s/m，转子和轴承的半径分别为Rr=0.06m、Rb=0.5m，将转子和轴承的对应长度记为Lr和Lb，取值分别是0.15m、0.3m。定子和转子的平均气隙长度为δ0=0.0045m，转子的质量偏心e0=0.0006m。励磁电流Ij=4A，碰摩擦系数f取0.01。将空气的磁导系数记为μ0，取值为4π×10-7H/m，µ为润滑油绝对黏度，取值为1.8×103Pa·s。

2.2.1 周期1的近似解

2.2.1.1 设置对照求解方法

为了评价HB-AFT 方法在碰摩转子系统周期解数值分析中的效果，将Runge-Kutta 方法作为对照组。Runge-Kutta方法是一种隐式或显式迭代法，在非线性微分方程的求解中具有重要应用，其优点为求解精度高，缺点为实现原理较复杂，不易操作[5]。

2.2.1.2 数值分析结果

数值分析结果具体如下。

首先，周期解的求解结果。水轮机大轴转速ω取值为13rad/s，轴径间隙设置为0.0002m，时域离散点的数量设置为144 个，迭代精度设定为1×10-11，谐波次数设置为8。根据隐式谐波平衡法的实施原理，通过MATLAB 软件求解出水轮机碰摩转子系统周期1 的近似解析表达式，将X方向的周期解记为X（t），Y方向的周期解记为Y（t），结果如下。

X（t）=-1.6432231×10-11+6.13443091×10-3sin（ωt）-1.1020326×10-11cos（2ωt）+1.61331×10-11cos（3ωt）+1.12521×10-10sin（3ωt）；Y（t）=0+6.1343138×10-4cos（ωt）+1.10925×10-10cos（3ωt）。

其次，求解方法性能评价。HB-AFT 求解法和Runge-Kutta 求解法在相同条件下得到的数值解如图2（a）所示，二者的数据高度吻合，说明求解结果具有良好的可信度。上述2 种方法求解的转子X方向时域图如图2（b）所示，其中τ为周期数。Runge-Kutta 法于大约第260 个周期达到稳态解，所用时间约为17.42s。与Runge-Kutta 法相比，HB-AFT 法更早达到稳态，所用时间约为7.72s。可见，HBAFT 法不仅具有较高的精确度，还能有效缩短求解时间。

图2 HB-AFT 求解法与Runge-Kutta 求解法性能对比

2.2.2 周期运动的稳定性分析

2.2.2.1 改变轴径间隙的周期解

在周期1 的运动分析中，将轴径间隙设置为0.0002m，为了进一步验证周期运行是否具有稳定规律，将轴径间隙扩大至0.0014m，其他模拟条件保持不变。同样利用HBAFT 法和Runge-Kutta 法进行迭代计算。HB-AFT 法在新条件下的X方向和Y方向周期解X1（t）和Y1（t）如下。

X1（t）=3.2755×10-8+2.82821×10-8cos（0.25ωt）-2.6488×10-1sin（0.25ωt）-2.4338×10-8cos（0.5ωt）-4.490×10-8sin（0.5ωt）-1.2406×10-8cos（0.75ωt）-1.6481×10-8sin（0.75ωt）-1.7878×10-7cos（ωt）。

Y1（t）=0+2.6144×10-1cos（0.25ωt）-2.8433×10-8sin（0.25ωt）+3.1124×10-8sin（0.5ωt）-1.2481×10-8cos（0.75ωt）+1.7214×10-8sin（0.75ωt）+1.7654×10-7sin（ωt）。

2.2.2.2 稳定性分析

Floquet 理论可用于分析周期运动的稳定性，通过特征乘子判断运动过程是否稳定。如果最大特征乘子小于1，表明周期运动是稳定的；当最大特征乘子大于1 时，表明周期运动不稳定（出现分叉）；如果最大特征乘子等于1，说明周期运动处于临界稳定状态[6]。设置不同的轴径间隙，计算最大Floquet 乘子，结果见表2。从表2 可知，当可调参数轴径间隙为0.0001m、0.0002m、0.0009m 和0.0014m时，系统呈现出稳定的周期运动，其他轴径间隙均出现了分叉。

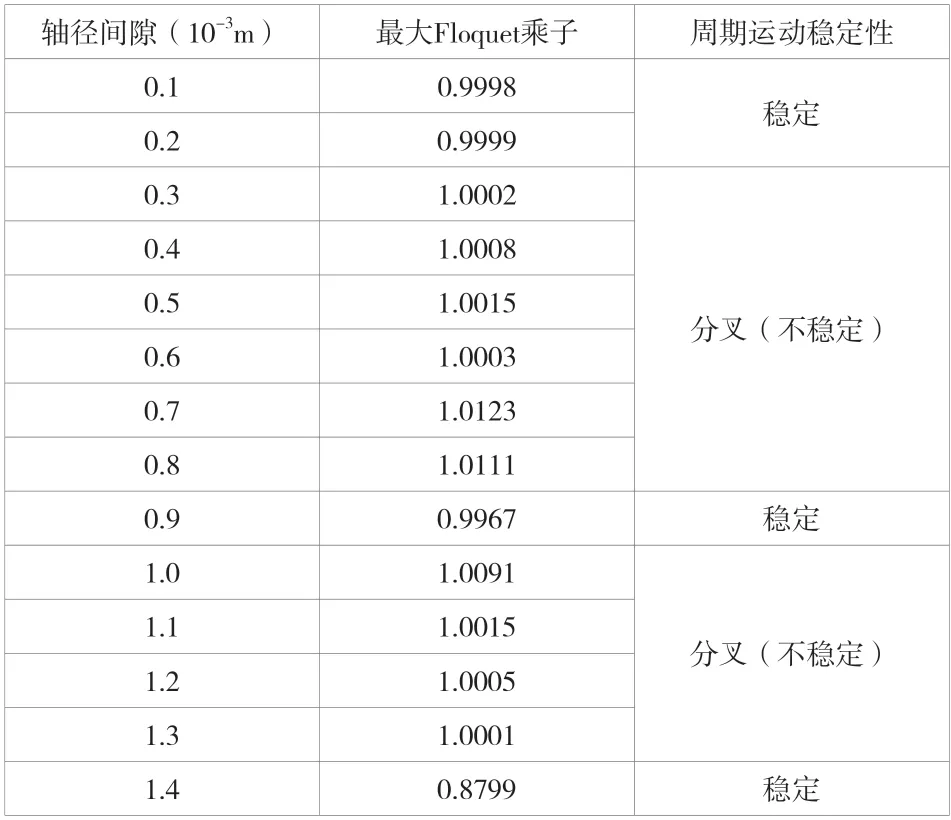
表2 不同轴径间隙对应的最大Floquet 乘子及周期运动稳定性结果

3 结语

对以上研究内容进行总结，得到以下3 个结论：第一，通过HB-AFT 法对碰摩转子系统的运动方程进行迭代结算，可有效求出X方向和Y方向的周期解。第二，与Runge-Kutta 法相比，HB-AFT 法均能达到基本相同的计算精度，计算耗时也有明显降低。第三，当轴径间隙为0.0001m～0.0014m 时，仅有0.0001m、0.0002m、0.0009m、0.0014m 共4 种取值能够使碰摩转子系统达到稳定运行状态。