基于改进遗传算法和支持向量机的轴流风扇优化计算

徐文静

（佛山市顺德区宏翼工业设计有限公司，广东 佛山 528000）

轴流风扇是飞机环控系统的重要组成部分，其作用是给飞机设备舱或飞机座舱提供再循环的动力[1-2]。合理的轴流风扇能够提高飞机飞行的安全性和节约生产成本，因此对轴流风扇优化计算进行研究具有重要意义[3]。

轴流风扇在航空航天、汽车和机械制造领域都有广泛应用，专家学者们对轴流风扇的优化设计也进行了大量研究。文献[4]利用CFD 建立了轴流风机参数优化模型，研究了风压、风量和转速等因素对轴流风机性能的影响，提出了一套可用于工程实际的轴流风机智能优化平台。文献[5]利用涡量分析法对轴流风扇的优化设计进行了分析，提出了一种轴流风扇结构优化计算模型，通过实例仿真验证了风机叶片增加导向筋可以显著提升轴流风扇的气动性能。文献[6]对便携式轴流风机的结构进行了优化设计，通过分析轴流风机的内部流动特性，确定了最优风扇叶片数量和最佳安装角度。

实际上轴流风扇的效率主要受机匣间距和叶片数量的影响，为此该文采用改进遗传算法和支持向量机对轴流风扇进行优化设计，以确定机匣间距和叶片数量的最优值，从而提高轴流风扇的机械性能。

1 支持向量机

支持向量机（Support Vector Machine，SVM）是Vapnik 等人提出的一种回归算法，由于SVM 在处理回归问题时受样本容量的影响较小，因此在交通、金融和医疗等领域得到了广泛应用。关于回归问题，SVM 的处理策略是利用核函数对样本数据进行映射，在高维空间利用最优超平面进行回归，以减少回归训练的计算量[7]。

SVM 最优超平面构造示意图如图1所示，令H为最优超平面，H可将图1 中的数据分为2 类，此时可以得到另外2 个超平面H1和H2，它们均与最优超平面H平行，H1、H2上的数据到H的距离最近，这些数据就是所谓的支持向量。

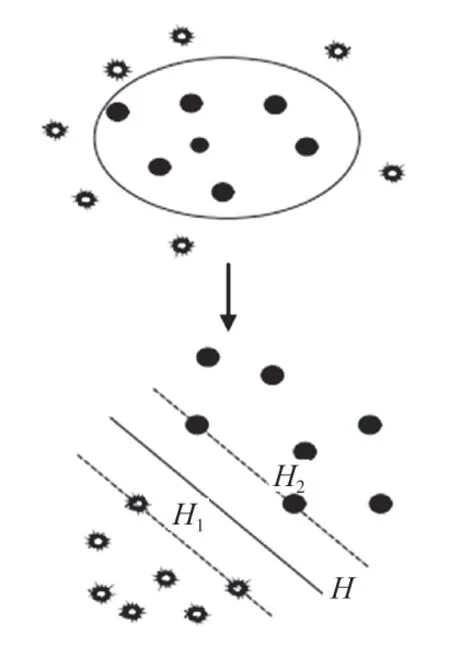
图1 SVM 最优超平面构造示意图

SVM 回归的基本原理如下。令样本容量为l的样本集合为zl={（x1，y1），…，（xl，yl）}，x∈Rn，y∈Rn，其中zi为样本容量l 集合，x为数量，y为输出量，构造如公式（1）所示的回归函数。

式中：f（x）为回归函数；x为数量；w为权值；b为偏置量。

为了控制训练误差，并保持回归函数的平滑，建立下列优化目标和约束条件，如公式（2）所示。

式中：w为权值；x为数量；y为输出量；b为偏置量；ε为误差。

由此可以得到公式（3）。

式中：C为惩罚因子，C∈（0，+∞）；|yi-f（xi）|g为不敏感函数。

不敏感函数满足公式（4）。

利用拉格朗日函数处理后，如公式（6）所示。

通过偏导计算可以得到公式（7）。

进而可以得到如公式（8）所示的对偶函数。

转化为矩阵后，如公式（9）所示。

式中：e=[1，…，1]T；Qi，j=（xi，xj）。

对公式（10）的矩阵进行求解，可以得到权值，如公式（10）所示。

根据KKT 条件，取得最优解应满足如公式（11）～公式（14）所示的条件。

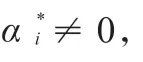
式中：SVs为所有支持向量样本集。

由此可以得到SVM 的回归函数，如公式（18）所示。

式中：K（xi，x）为核函数。核函数可以完成SVM 的线性到非线性转换，它的作用是将低维空间中的样本数据映射到高维空间进行求解，避免低维空间的维度灾难，降低求解难度。SVM 的核函数有多种，应用不同的核函数会使SVM 的性能有所不同，目前应用较多的有多项式核函数、Sigmoid 核函数和径向基核函数。非线性回归问题通常将径向基核函数作为SVM的核函数，其表达式如公式（19）所示。

式中：σ为核参数。

2 改进遗传算法

2.1 遗传算法

遗传算法[8]（Genetic Algorithm，GA）是Holland 等人受生物遗传原理的启发提出来的，其原则是优胜劣汰，通过选择、交叉和突变等操作完成生物进化，以寻找优化问题的最优解。GA 算法通过下列7 个步骤实现种群进化，具体如下。

第一，初始化编码。对优化问题的编码进行初始化，并将其转化为二进制编码。

第二，初始化种群。随机生成初始种群W=（W1，W2，…，WN），其中W为种群，N为种群容量。

第三，计算个体适应度值。根据优化目标定义适应度函数。

第四，执行选择操作。根据个体适应度值的好坏进行排序，保留适应度值更好的个体进入下一代，目前常采用轮盘赌法进行选择，选择概率的计算如公式（20）所示。

式中：pi为第i个个体被选中的概率；fi为第i个个体的适应度值，i=1，2，...，N。

第五，执行交叉操作。交叉操作的依据是生物遗传定律，其表达式如公式（21）、公式（22）所示。

式中：Wqi、Wsi均为基因；b为随机数，b∈[0，1]。

第六，执行突变操作。在GA 算法迭代过程中可能会陷入局部最优，为了避免该问题，需要执行突变操作，其表达式如公式（23）、公式（24）所示。

式中：Wmax、Wmin分别为Wij的最大值和最小值；g、Gmax分别为当前进化代数和最大进化代数；r、r2为随机数，r、r2∈[0，1]。

第七，重复执行选择、交叉和突变等操作，即可找到优化问题的最优解。

2.2 改进遗传算法

研究表明，GA 算法在寻优过程中，交叉概率和突变概率始终为固定值，导致算法出现不收敛的现象。为了提高GA 算法的优化性能，该文利用种群平均适应度值对交叉概率和突变概率进行动态调整，如公式（25）所示。

式中：Pc为交叉概率；Pcmax为Pc的最小值；N为种群容量；favg为种群平均适应度值；Pca为交叉概率调整系数；Pm为突变概率；Pmmax为Pm的最大值，Pma为突变概率调整系数。

IGA 算法的交叉概率和突变概率经过动态调整后，在迭代前期，种群的多样性更好，有助于算法展开全局搜索。而在迭代后期，种群的局部搜索性能更强，有助于算法跳出最优解，加快算法收敛。

3 轴流风扇参数优化计算

机匣间距和叶片数量是影响轴流风扇效率的主要参数，两者并非简单的线性关系，无法通过线性拟合确定二者之间的函数关系，为此该文采用支持向量机和改进遗传算法解决上述问题。

3.1 基于SVM 的风机参数拟合

某型号轴流风扇效率与风机叶片数量和机匣间距组成的样本数据见表1，利用表1 中的数据对SVM 模型进行训练，确定风机效率与风机叶片数量和机匣间距之间的函数关系。

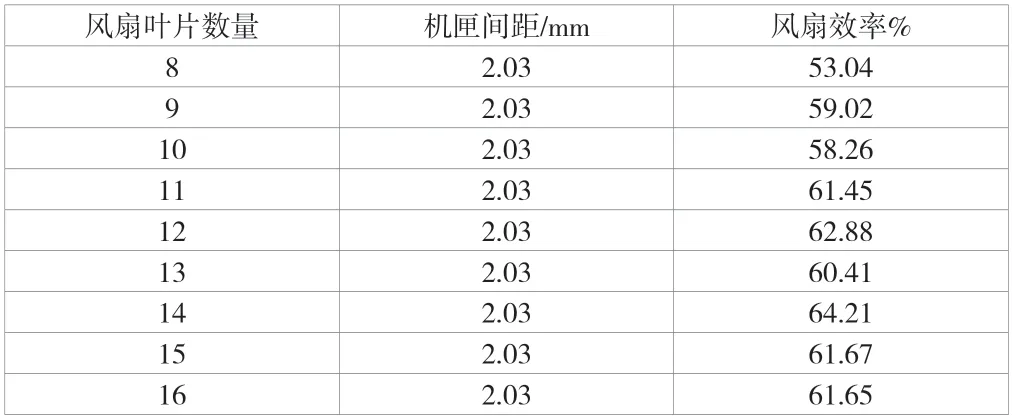
表1 轴流风扇样本数据

训练完成后，利用另外3 组测试数据对SVM 模型的计算效果进行检验，具体见表2。由表2 可知，3 组测试数据的测试误差均在0.05%以内，满足工程要求。由此可见，基于SVM的风机参数拟合是合理的。

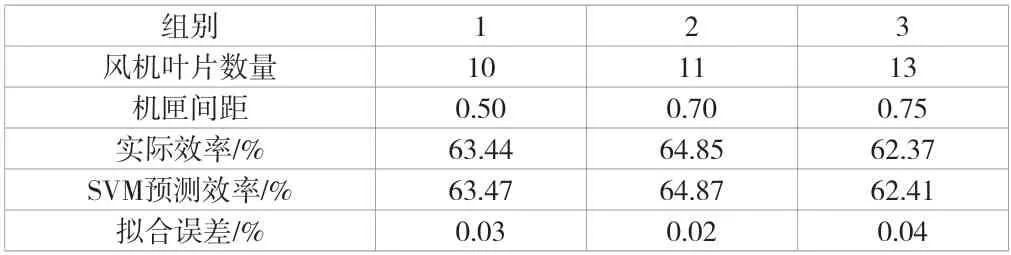
表2 SVM 预测结果

3.2 基于IGA 算法的性能参数寻优

轴流风扇效率与风机叶片数量和机匣间距之间存在一定的函数关系，为此，该文采用所提IGA 算法对轴流风扇效率的最大值进行计算，并采用GA 算法进行对比和分析。

IGA 算法的参数设置如下[9]：种群容量为30，最大迭代次数为300，突变概率最小值和交叉概率最大值分别为0.5 和0.05。将GA 算法的突变概率和交叉概率设为固定值，其值分别为0.7 和0.04，其余参数保持不变。

采用IGA 算法和GA 算法对轴流风扇效率进行优化，2 种算法的收敛曲线如图2所示。对比图2 中的2 条收敛曲线可知，IGA 算法的迭代次数更少，最优适应度值更好。

图2 IGA 算法和GA 算法的收敛曲线

IGA 算法和GA 算法的收敛结果见表3。对比表2 中的数据可知，IGA 算法只需要65 次迭代即可找到最优适应度值，其值为73.31%，IGA 算法优化效果更好，此时对应的风机叶片数量和机匣间距分别为12 和0.65mm。由此可见，当风机叶片数量为12、机匣间距为0.65mm 时，轴流风机效率最高。

表3 IGA 算法和GA 算法收敛结果对比

4 结论

该文提出了一种基于改进遗传算法和支持向量机的轴流风扇优化计算方法。采用支持向量机对轴流风扇效率、风机叶片数量和机匣间距之间的函数关系进行了拟合，利用改进遗传算法对轴流风扇效率的最大值进行了计算。结果表明，当风机叶片数量为12、机匣间距为0.65mm 时，轴流风机最大效率为73.31%，并通过与遗传算法对比验证了该文所提方法的正确性和优越性。