天体运动中应澄清的两类问题
2023-10-30邵立凯
邵立凯
(山东省青岛即墨区第五中学)
天体运动中,有两类问题是学生一直比较困惑的,一是天体椭圆运动中万有引力和向心力的关系,二是天体圆周运动中不同质量天体的机械能关系.笔者调查发现,学生在第一类问题上出错的根源是对万有引力公式和向心力公式中的“r”认识有偏差,误认为二者是相同的;第二类问题出错的根源则是受思维定式的影响,将引力势能与重力势能零势能的选取混为一谈,没有认识到二者的区别所在.鉴于此,笔者对两类问题分别予以辨析,以正本溯源,澄清错误,促进学生对该类问题的深度认识.
1 椭圆运动中万有引力和向心力的关系
1.1 问题引入
如图1所示,天体m绕天体M运动,其运动轨迹为椭圆,天体M处在椭圆的一个焦点上,当天体m运动到A点 或B点时,所受万有引力和向心力的大小关系如何?
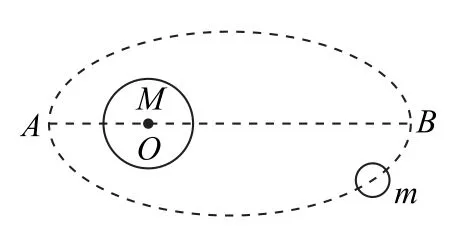
图1
下面结合椭圆的基本知识,从万有引力的作用效果进行讨论.
1.2 分析问题
以天体m运动到B点为例,设OB间的距离为rB,天体m运动到B点的速度大小为vB,在B点,天体m所受万有引力F万与其速度vB垂直,如图2所示.在该位置,天体m无切向加速度,只有法向加速度,故其所受万用引力与向心力相等,即,需要注意的是中的rB和中的并不相同,rB表示天体m到M中心间的距离,则表示椭圆在B位置的曲率半径,结合椭圆知识可知a2=b2+c2,rB=a+c,则;同理在A点,天体所受万有引力与向心力亦相等,即有,其中rA=,则b、c分别为椭圆的半长轴、半短轴和半焦距,如图3所示.
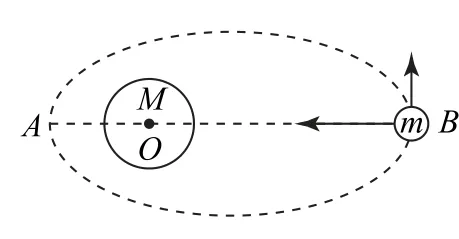
图2

图3
例1“天问一号”探测器成功在火星软着陆,标志着我国成为世界上第一个首次探测火星就实现“绕、落、巡”三项任务的国家.“天问一号”在火星停泊轨道运行时,近火点距离火星表面的高度为h1,运动至该点时的速度大小为v1,远火点距离火星表面的高度为h2,运动至该点时的速度大小为v2.已知火星半径为R,质量为M,“天问一号”的质量为m,万有引力常量为G,则下列说法正确的是( ).
2 圆周运动中不同质量天体的机械能关系
2.1 问题引入
如图4所示,两颗人造卫星A和B都围绕地球做匀速圆周运动,其质量之比为mA∶mB=1∶4,周期之比为TA∶TB=1∶8,则卫星A和卫星B的机械能大小关系如何?

图4
2.2 分析问题
部分学生之所以认为卫星A的机械能小于卫星B的机械能,是将卫星的引力势能类比为地面附近的重力势能造成的,对于地面附近不同高度处的物体,可认为同时处于地面附近,因此可以取地面为零势能面,而对处于不同轨道的卫星而言,不能认为同时处于地面附近,除非它们离地面的高度远小于地球的半径,故不能取地面为零势能面,必须取无穷远处为零势能点.根据势能的定义可知,将质量为m的物体由距地心为r处移动到无穷远处,万有引力做的功即为物体在r处所具有的引力势能,其大小为Ep=,则对卫星A有EpA=,对卫星B有,又mA∶mB=1∶4,rB=4rA,故有EpA=EpB,结合EkA=EkB,可知卫星A和卫星B的机械能相同.
例2地球对其周围的物体产生的万有引力是通过地球周围的引力场产生的,物体在引力场中具有的势能被称为引力势能.若规定距地球无限远处为引力势能零点,可得到在半径为r的轨道上做匀速圆周运动的人造地球卫星引力势能的表达式Ep=,其中M为地球的质量,m为卫星的质量,G为万有引力常量.
(1)若一质量为m的人造地球卫星在半径为2r的轨道上做匀速圆周运动,则其机械能为多少?
(2)已知在地球表面附近,对于质量为m的物体离开地面高度为h时,若规定地球表面为重力势能零点,物体重力势能的表达式为E0=mgh(g为重力加速度),这个表达式虽然与题干中引力势能的表达式在形式上有很大的差别,但二者本质相同,试证明在忽略地球自转的情况下,当h远小于地球半径R时,重力势能和引力势能的表达式是一致的.(可能用到的数学知识:当|x|≪1时,
在教学的过程中,教师对于学生存在的疑虑或困惑,决不能单凭几个结论去解决问题.要尽可能从源头上厘清知识的来龙去脉,促进学生对该部分知识的深度认识.只有这样,才能从根本上消除学生心中的困惑,真正提升学生分析问题和解决问题的能力.
(完)
