城市盾构隧道下穿对既有桥梁的影响分析

2023-10-30郑恒重周斌

建材与装饰 2023年32期

郑恒重，周斌

（广东省重工建筑设计院有限公司，广东广州 510670）

0 引言

随着我国城市化人口增加对交通出行的需求与日俱增。而城市地面交通发展逐渐受到空间条件的限制。城市地下轨道因其客运量大和准时方便的优势已成为各个城市重点发展的重点。城市轨道的线路不可避免的会遇到侧穿既有城市桥梁基础。由于盾构隧道的开挖会影响到周围原状土体，对土体与既有桥梁桩基的相互作用产生扰动，最终导致桥梁桩基在盾构开挖过程中产生位移。在位移达到一定程度后，因位移而增加的荷载将严重影响既有桥梁安全性与稳定性[1-2]。

研究表明盾构在中风化泥质砂岩中穿越高铁桥梁基础时可通过合理布置洞内壁后二次注浆加固方案，避免同类工程常见的隔离桩施工[3]。通过运用有限元分析软件模拟双线隧道下穿桥梁，结果表明地表的沉降曲线为单峰“V”字形正态分布[4]。以西安地铁十六号线下穿城市高架桥为背景进行数值模拟，结果表明地铁隧道开挖对既有桥梁桩基影响，临近隧道的桩基变形影响最大，沉降值达到7.14mm，而且后开挖隧道桩基变形规律为先增大后减小的趋势[5]。

本文以广州城市轨道交通地铁某线下穿既有桥梁为工程背景，通过midas GTS NX 与midas civil 三维模型模拟盾构隧道施工时桩基变形对既有桥梁的影响，并采用LEC 法对盾构隧道下穿既有桥梁进行风险评估分析。

1 工程概况

广州市轨道交通某线区间隧道长约950m，采用盾构法施工。隧道外径D6.4m，内径D5.5m。隧道在ZDK17+446.551—ZDK17+531.850、YDK17+448.108—YDK17+531.850 穿越既有高架桥，左右线区间侧穿现状桥梁83#、84#墩1～4#桩基，其中右线区间隧道距离83#桥墩83-2 桩基最近距离为1.9m；左线区间隧道距离84#桥墩84-1 桩基最近距离为19.4m；隧道穿越长度约为19m。既有高架桥建于2000 年。该桥为单幅桥，垂直路宽幅度为19m。区间下穿位置桥梁联长110m，上部结构采用（30+50+30）m 预应力混凝土现浇连续箱梁。下部结构为薄壁墩+承台桩基础，主墩采用墩梁固结形式。桩基为钻孔灌注桩，直径为1.5m。83#桩桩长27.16m，84#桩桩长33.34m。

隧道范围地层为中风化泥质粉砂岩<8-1>、中风化泥质粉砂岩<8-3>、强风化泥质粉砂岩<7-3>，地面至隧道拱顶自上而下地层为粉质黏土<5N-2>、粉质黏土<4N-2>、中粗砂<3-2>、淤泥质中粗砂<2-3>、淤泥质土<2-1B>、淤泥<2-1A>、杂填土<1>。

2 有限元分析

2.1 研究思路

为分析地铁施工对既有高架桥的影响，采用迈达斯GTS NX 2015 建立三维模型模拟隧道施工变形。采用迈达斯CIVIL2020 模拟既有桥梁结构，将隧道施工产生的变形施加到既有桥梁桩基，研究既有桥梁结构内力变化。

2.2 模型的建立

根据既有高架桥竣工图，结合桥墩、桩基、承台构造和地层特性，对下穿盾构隧道建立三维有限元模型，模型尺寸为147m×110m×55m。本计算模型地层厚度自上而下分别为：杂填土2.19m，淤泥质土2.70m，粉质黏土3.00m，淤泥质土2.80m，粉质黏土1.80m，强风化粉砂质泥岩2.90m，强风化粉砂质泥岩下为角砾状构造破碎带（表1）。计算模型中的土层采用实体单元，其本构模型采用各向同性弹塑性模型中的修正莫尔-库伦模型，其破坏准则为MohrˉCoulomb 破坏准则。桥梁桩基采用一维梁单元；盾构隧道衬砌采用二维平面板单元；桥墩和承台采用实体单元，其材料本构模型均为各向同性弹性模型。

表1 三维数值模拟材料参数取值

采用有限元分析程序Midas Civil 2020 建立有限元模型进行整体静力分析。上部结构为预应力混凝土连续箱梁，下部结构为花瓶墩，桩基约束采用桩土弹簧模拟。桥梁模型计算荷载及组合如下。

（1）永久作用。上部结构的沥青混凝土桥面铺装自重计算采用容重24kN/m3；钢筋混凝土自重计算采用容重26kN/m3；旧桥成桥20 年永久沉降考虑10mm；桩基新增不均匀沉降根据岩土模型计算结果取值。

（2）可变作用。本桥为连续箱梁，当按照单梁模型进行计算时，汽车荷载需考虑偏载效应，综合计算得活载效应系数为：4×0.67×1.15＝3.082。均匀温度作用为整体升温20℃，整体降温-20℃；梯度温度按《公路桥梁设计通用规范》规范执行。

2.3 模拟结果分析

模型计算工况为初始场地（位移清零）：跨线桥和车站施工；位移清零；盾构隧道施工（先施工隧道右线，隧道右线通过后施工隧道左线）。以下为右线隧道下穿前、下穿时、下穿后、左线隧道下穿前，下穿时和下穿后的位移计算结果如表2 所示。

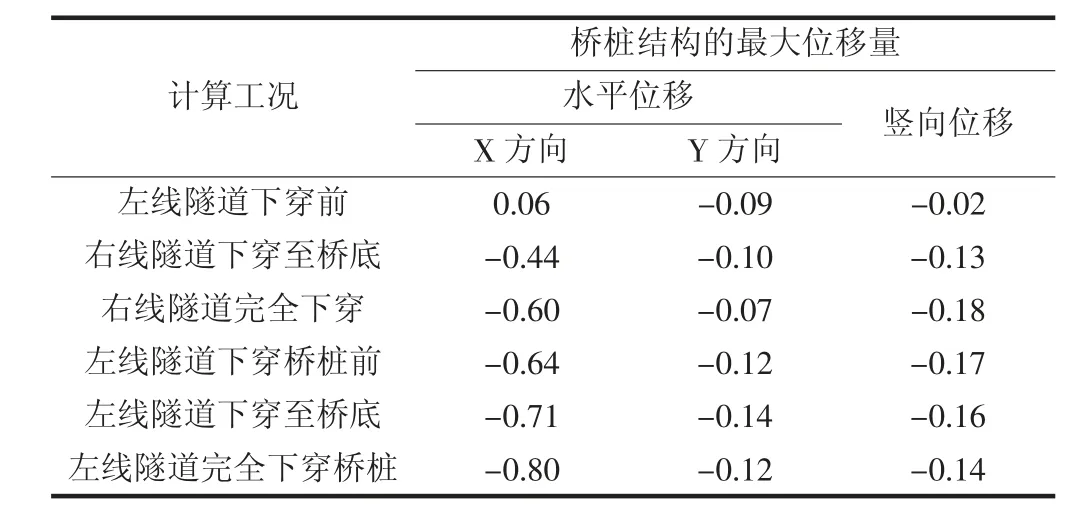
表2 桥桩结构位移汇总单位：mm

由表2 计算结果可知，隧道下穿过程中X 方向位移大于Y 方向、竖向位移，且盾构过程中X 方向位移增加速率较大。X 方向位移最大值出现在左线隧道完全下穿桥桩后为-0.80mm。Y 向水平位移与竖向位移随着盾构进行位移增加速率较X 方向速率小。其中Y 方向位移极值为-0.14mm，出现在左线下穿至桥梁底时；竖向位移最大值出现在右线隧道完全下穿，竖向位移极值为-0.18mm；

将桩基变形结果通过强制位移施加到CIVIL 桥梁模型中，对既有桥梁进行检算，结果如表3 所示。

表3 既有桥梁计算结果汇总（一）

由表3 可知，隧道下穿过程中，桩基产生的位移对桥梁影响可控，既有桥梁各项设计指标均满足设计规范要求。

本项目施工诱发高架桥最大差异沉降为0.18mm，最大差异水平位移为0.8mm。由于83#墩与盾构隧道水平距离较近，因此在施工过程中产生的差异沉降与水平位移最大。为探讨该差异沉降控制作用下桥梁的承载力安全状态，假设既有产生15mm 差异沉降，5mm差异水平位移，对桥梁进行结构验算，结果如表4 所示。

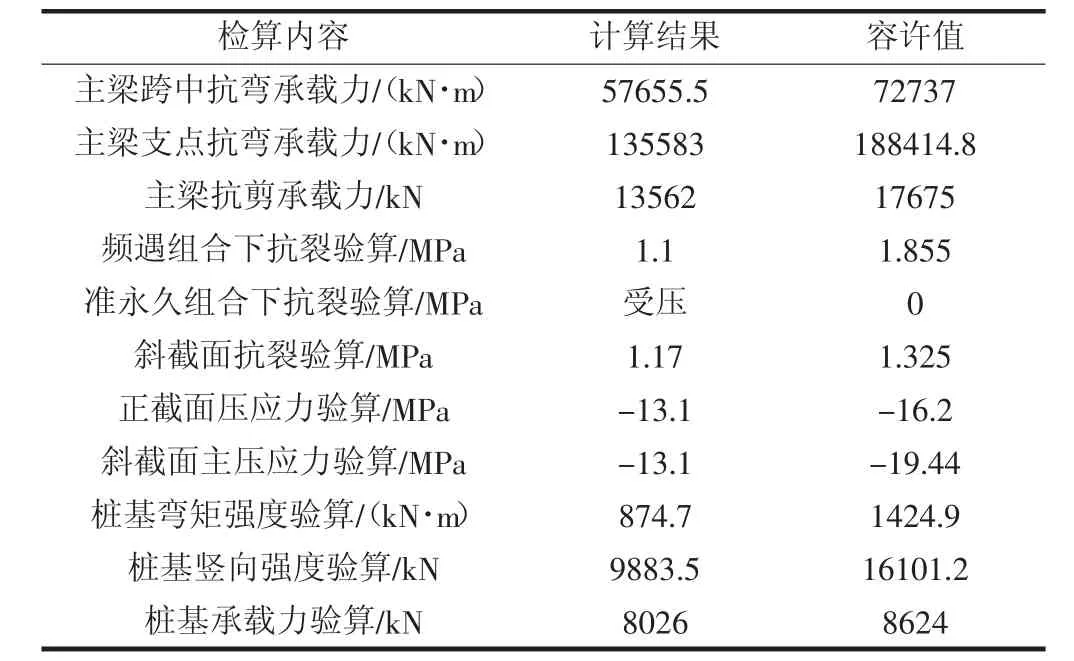
表4 既有桥梁计算结果汇总（二）

经测算，水平位移5mm 时，差异沉降10mm 时，桥梁上部结构应力验算均满足要求，桩身强度验算均满足要求。根据《城市桥梁隧道结构安全保护技术规范》6.4.1 规定，竖向差异可定沉降控制值为10mm，水平位移控制值为5mm，监测预警等级及应对管理措施如表5所示。

表5 监测预警等级划分及对应管理措施

3 风险分析评价

选择LEC 法对盾构施工（地下水位控制）、同步注浆、二次注浆、回填注浆进行风险估测如式（1）所示。

式中：L——发生事故的可能性大小；E——人体暴露在这种危险环境中的频繁程度；C——一旦发生事故会造成的损失后果；D——危险性。

为了简化计算，将事故发生的可能性、施工人员暴露时间、事故发生后果划分不同的等级并赋值。根据式（1）可计算作业的危险程度，并判断评价危险性的大小。将结果按下表分级。D 值越大，危险性大。本项目各评价单元危险性评价如表6 所示。需要增加安全措施，或改变发生事故的可能性，或减少人体暴露于危险环境中的频繁程度，或减轻事故损失，直至调整到允许范围内。