面向E级计算的线性代数解法器研究综述
2023-10-29何连花
何连花,徐 顺,金 钟
中国科学院 计算机网络信息中心,北京 100190
数值线性代数算法是大多数科学算法的支柱,大量科学与工程问题最终都归结为数值线性代数即矩阵计算问题。数值线性代数主要研究线性方程组求解、特征值问题、奇异值分解、最小二乘问题等,目前已经存在非常多的优秀算法来求解这些问题[1-5]。
数值线性代数解法器的发展可以追溯到20世纪70 年代,以LINPACK(linear system package)的产生为标志。此后,产生一系列优秀的数值线性代数解法器,为科学计算提供了有力的支撑。实现块操作优化的LAPACK(linear algebra package)[6]在20 世纪80 年代被正式推出(http://www.netlib.org/lapack/)。1995年用于并行分布式多核系统的ScaLAPACK(scalable linear algebra package)[7]产生了。随着多核处理器的出现,关注多核计算的PLASMA(parallel linear algebra software for multi-core architectures)[8-9]在2008年被正式推出。同时,随着GPU的出现,GPU版本的线性代数库MAGMA(matrix algebra on GPU and multicore architectures)[10]产生。最近几年,随着准E 级机及E级机的出现,出现了很多面向E级机架构设计的数值线性代数解法器,例如美国的SLATE(software for linear algebra targeting exascale)[11]、中国的xMath[12]、日本的KMATHLIB(https://www.r-ccs.riken.jp/labs/lpnctrt/projects.html)。如图1 所示,可以明显看出数值线性代数解法器一直随着计算机体系结构的变化而发展。

图1 稠密矩阵数值线性代数解法器发展Fig.1 Development of dense matrix numerical linear algebra solvers
本文总结了国外高性能数值线性代数解法器已有工作,特别关注主流稠密及稀疏线性代数解法器面向现代体系架构在功能及性能方面的优化。介绍了稀疏线性代数解法器,包括:PETSc(portable,extensible toolkit for scientific computation)[13]、Trilinos[14]、Hypre[15]、Ginkgo[16]、SuperLU[17]/STRUMPACK(structured matrix package)[18]。
1 E级架构特点和挑战
如今,高性能计算(high-performance computing,HPC)正处于一个关键时刻,计算机体系结构多方面的结合,给数值线性代数算法的发展,既带来了挑战,又提供了机遇。本章首先介绍E级架构具有的特点,然后介绍数值线性代数算法研究趋势。
1.1 E级架构特点
当今高性能计算机具有如下特性[19]:
(1)异构化
目前各种异构架构的CPU(如:x86、ARM、Power)不断涌现,同时各种基于不同体系结构的计算加速部件(如:GPU、张量处理器(tensor processing unit,TPU)、FPGA(field-programmable gate array)、其他应用专用加速卡)也陆续出现。E级计算机节点数量很大,且每个节点都包含一个重量级多核处理器和许多重量级硬件加速器。大规模并行和异构体系结构给并行编程带来巨大困难。
(2)数据传输成本变高
目前,超级计算机的浮点性能增长速度超过了内存访问性能或节点间通信性能。这导致计算速度和数据传输速度之间存在严重差异,预计这种差异在未来会越来越大。可以将数据传输性能大概分为延迟和吞吐量。延迟的影响在AllReduce 类型通信中最为突出(如内积、范数)。
(3)能耗增加
目前Top500排名前十的超级计算机的功耗已普遍在MW 甚至10 MW 量级,而E 级计算机功耗将达到30 MW,这给大规模应用的运行带来了极高的能耗成本。尽管很多芯片设计和制造技术能够根据实时负载等信息降低微处理器功耗,但在数值算法设计和实现层面依然需要考虑降低能耗。
(4)拥有多种精度的浮点运算
在E级大规模科学计算中,双精度运算不足的情况会比现在更频繁地发生。但以四倍精度执行所有运算的成本太高。支持多种精度的GPU异构计算在超算环境已普遍应用,这也为混合精度计算提供了必要的硬件基础。
(5)故障率增加
随着技术的进步,大规模集成电路(large-scale integration,LSI)的工艺规则将变得更加精细,从而允许更多的组件集成到一台机器中。尽管这将显著提高超级计算机计算能力和效率,但也带来了可靠性和故障率方面的挑战。
1.2 数值线性代数算法研究趋势
算法、软件和硬件都至关重要。随着E级机器的诞生,数值线性代数算法也需要不断更新以便满足各个领域的应用需求。本节将简单介绍数值线性代数算法领域最近的一些研究方向(见图2),这些研究旨在应对1.1节所提出的挑战。
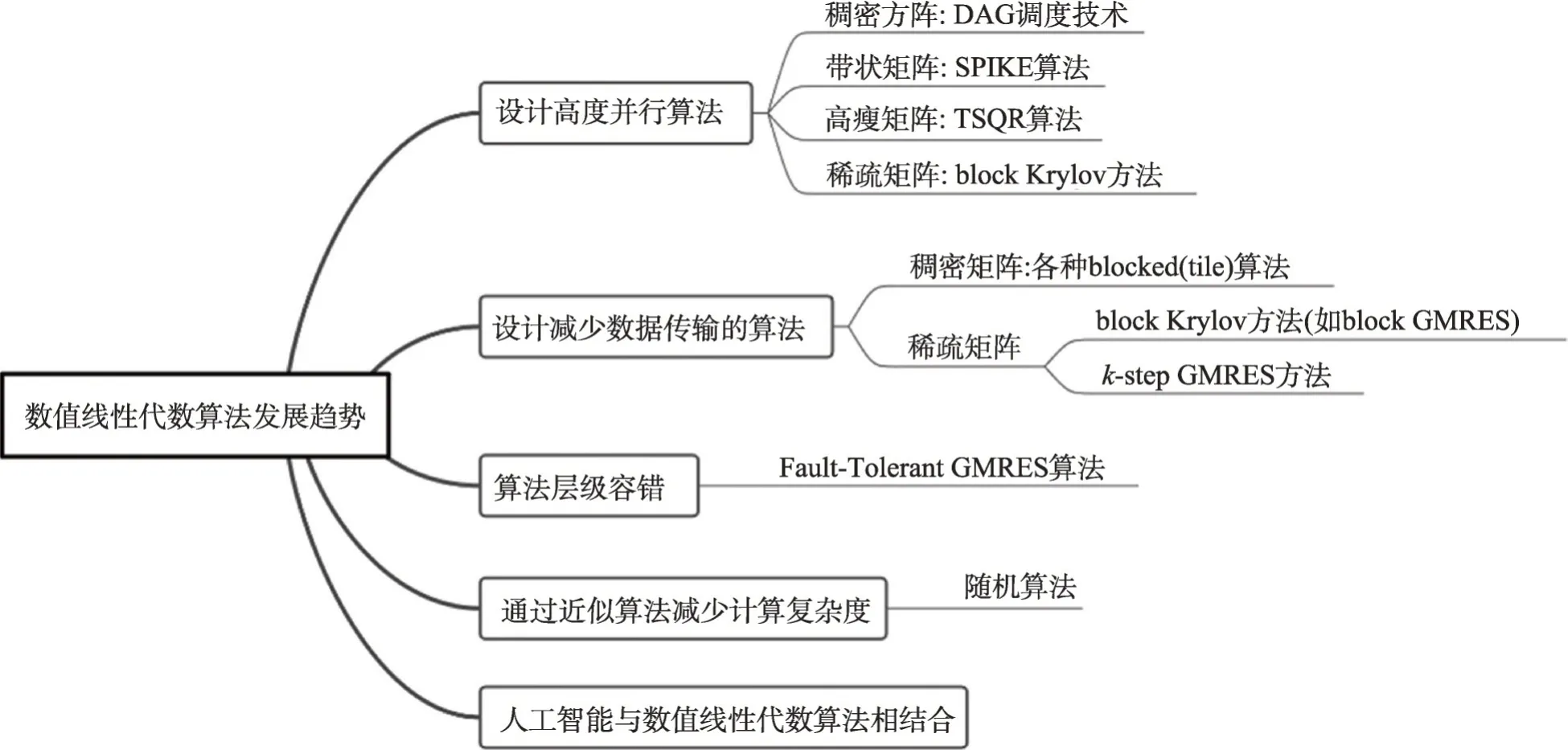
图2 数值线性代数算法发展趋势Fig.2 Research trends of numerical linear algebra algorithms
(1)设计具有高度并行性的算法
为了利用超级计算机的计算核心,数值线性代数算法需要具有高度的并行性。对于稠密矩阵,最近十年基于有向无环图(directed acyclic graph,DAG)[20]的调度技术已经成为标准技术之一。针对高瘦矩阵的QR分解,提出了基于分而治之策略的TSQR算法[21]。对于稀疏矩阵,目前块Krylov方法被广泛使用。
(2)减少数据传输量
在E级机上,主内存访问和节点间通信等数据传输的成本远高于计算。因此,有必要尽量减少数据传输量。在内存层次结构中,较高级别的存储速度更快,但容量有限,而较低级别的存储容量较大,但数据传输速度较低。因此,通过提高数据可重用性,并在数据位于缓存等上层存储中时对数据执行尽可能多的计算,可以最大限度地减少来自较低层存储的数据传输并提高性能。目前使用各种block 方法(例如block GMRES(generalized minimal residual algorithm)方法)可有效减少数据传输量。
(3)降低能耗
这些新的机器特征,要求新一代数值线性代数算法应尽可能最大限度地降低能耗。国内外有很多学者努力通过改进数值线性代数算法以达到降低能耗的效果。2014年,Tan等人[22]对改善高性能数值线性代数运算的功率和能耗的技术进行概述总结。
(4)混合精度算法
目前已经有很多工作关注混合精度数值线性代数算法,Abdelfattah等人[23]对混合精度数值线性代数算法进行了全面的总结。研究表明混合精度算法的性能超过了在高精度下运行的传统算法。对于性能受限的稠密线性代数算法,采用低精度误差矫正的混合精度迭代更新(iterative refinement,IR)算法仍然是利用低精度计算能力的首选算法。对于稀疏线性代数,算法的内存约束性质使将内存精度与算术精度解耦的思想更具发展前景。此外,有效的预处理器精度调整,可以在不影响迭代求解器收敛的情况下节省运行时间。2022 年,Higham 等人[24]对数值线性代数中混合精度算法进一步概述总结。
(5)算法层级容错
目前已经出现一些具有算法级容错能力的数值线性代数算法,例如Fault-Tolerant GMRES 方法[25]。但目前这方面的研究还远远不够,需要新的范式将算法容错、应用程序容错以及系统容错综合考虑。
2 稠密线性代数解法器
在稠密数值线性代数中,求解线性方程组Ax=b时,一般先将矩阵A分解为具有一定规律的矩阵的乘积,然后通过向前回代和向后回代(有时计算矩阵的逆),从分解的矩阵中轻松求解x。不同的矩阵分解适用于特定的问题类别。图1 展示了稠密线性代数解法器的发展历程,数值线性代数软件库在不断进行优化以便适应新的体系架构,从而发挥出更好的计算性能。本章分别介绍了ScaLAPACK、PLASMA、MAGMA及SLATE的功能,且表1汇总了它们的特点。
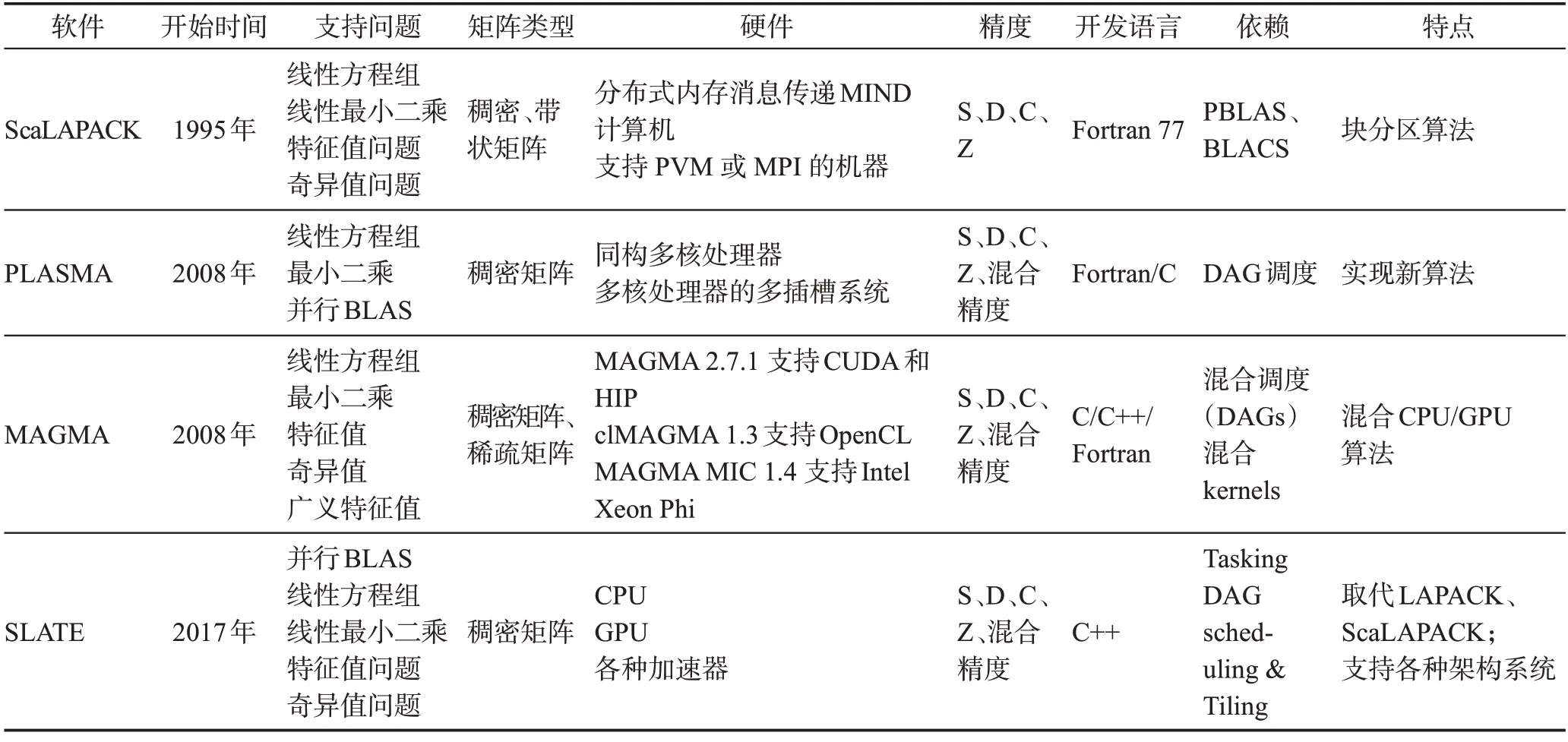
表1 ScaLAPACK、PLASMA、MAGMA及SLATE特点汇总Table 1 Summary of ScaLAPACK,PLASMA,MAGMA and SLATE features
2.1 ScaLAPACK
ScaLAPACK(http://www.netlib.org/scalapack/)是一个高性能线性代数库,适用于分布存储的多指令流多数据流(multiple instruction multiple data,MIMD)并行机,例如Intel Paragon、IBM SP 系列和Cray T3 系列。此外,该软件的设计使其可以通过网络环境与工作站集群一起使用,并通过PVM(parallel virtual machine)或MPI(message passing interface)与异构计算环境一起使用。
ScaLAPACK 可以在任何支持PVM 或MPI 的机器上运行。ScaLAPACK 可以求解线性方程组、线性最小二乘问题、特征值问题和奇异值问题,可以处理矩阵分解或估计条件数等,可求解稠密和带状矩阵。ScaLAPACK 主要设计思想包括:将数据矩阵以块状循环分布的方式分布到各进程上;使用块分区算法以确保高质量的数据重用,减少内存层次结构中不同级别之间的数据移动频率。ScaLAPACK基本构建模块是PBLAS(parallel basic linear algebra subprograms)和BLACS(basic linear algebra communication subprograms)。
2.2 PLASMA
PLASMA(https://bitbucket.org/icl/plasma)是 由美国田纳西大学开发的稠密线性代数包,主要目的是解决LAPACK 和ScaLAPACK 库在多核处理器上的性能缺陷。PLASMA目前提供了一系列用于求解线性方程组、最小二乘问题、特征值问题和奇异值问题的例程。在过去的十年中,PLASMA 已经被广泛用于使用英特尔CPU处理器、IBM POWER处理器和ARM 处理器的各种系统中。PLASMA 的设计是为了超越LAPACK 和ScaLAPACK,主要是通过重构软件结构,尽可能在基于多核处理器的现代计算机上实现更大的效率,同时实现新的或改进的算法。然而,目前由于功能有限,PLASMA 并不能完全取代LAPACK。PLASMA 旨在为多核处理器系统提供高性能服务,这一目标是通过结合并行算法、系统调度和软件工程中最先进的解决方案实现的。特别是,PLASMA是围绕以下三个概念构建的。
(1)Tile矩阵布局
PLASMA 采用基于tile 的存储方法。矩阵被细分为相对较小的方块,称为tiles,每个方块占据一个连续的内存区域。Tiles被有效地加载到缓存中。使用tiles 布局可最大程度地减少冲突cache 失效、TLB(translation lookaside buffer)失效和错误共享,并最大限度地提高预取(prefetch)的能力。PLASMA 包含并行和缓存高效的例程,用于在传统的LAPACK布局和tile 布局之间进行转换。PLASMA 目前存储两个版本的矩阵,因此它的内存需求比LAPACK大。
(2)Tile算法
PLASMA 引入了重新设计的新算法,从而最大限度地提高多核系统缓存级别的数据重用率。tiles被加载到高速缓存中,并在被传回主内存之前被完全处理。对小tile的操作产生了细粒度的并行性,从而提供足够的工作以保持大量的核心占用。
(3)动态调度
PLASMA 依赖于顺序任务的并发运行时调度。运行时调度基于在任何给定的时间点上根据处理数据的可用性将工作分配给内核的想法,因此有时也称为数据驱动调度。该概念与通过DAG表达计算的想法密切相关,并且在运行时采用DAG 的灵活性。这与fork-and-join 调度(ScaLAPACK 所采用的)直接相反,fork-and-join 调度中人工同步点暴露了代码的串行部分,在顺序执行时多个内核处于空闲状态。PLASMA最初使用的是自制的QUARK运行时调度器。目前,PLASMA 依靠OpenMP(open multi-processing)进行动态、基于任务的调度[26]。
DPLASMA(distributed parallel linear algebra software for multicore architectures)[27]通过PaRSEC(https://icl.utk.edu/parsec)运行时系统将PLASMA 算法扩展到分布式环境,并使用CUDA(compute unified device architecture)支持GPU 加速器。在DPLASMA 中,许多算法使用参数化任务图(parameterized task graph,PTG)来描述任务和依赖关系,其中每个任务通过state-space描述其所有后续任务。在此表示中,不需要在运行时推断任务依赖关系,并且可以有效地执行PTG。
Chameleon(https://project.inria.fr/chameleon/)[28]以不同方式扩展了PLASMA 算法,从而可以支持各种运行时系统:QUARK、OpenMP、PaRSEC或StarPU(https://starpu.gitlabpages.inria.fr)。其中PaRSEC 和StarPU 支持分布式环境和使用CUDA 的GPU 加速器。在DPLASMA 和Chameleon 中使用高级运行时是一个成功的策略。但面临的困难是它与运行时相关,这往往需要与运行时的开发者密切协作。例如,增加ROCm或oneAPI的支持很可能需要首先在运行时中增加这种支持。
2.3 MAGMA
MAGMA(https://icl.utk.edu/magma/)是用于异构/混合架构的线性代数软件包,MAGMA 是由开发LAPACK 和ScaLAPACK 的团队设计和实现的,融合了混合避免同步和通信避免算法以及动态运行时系统的最新发展。MAGMA 库的设计在功能、数据存储和接口方面与LAPACK 相似,从而用户可以轻松地将他们现有的应用程序从LAPACK 移植到MAGMA,以便充分发挥混合架构的计算能力。
许多科学计算既需要解决大型数值线性代数问题(如BLAS、卷积、奇异值分解线性系统求解器),也需要批量求解可以并行求解的并发小问题。MAGMA包括完善的求解大型矩阵的能力,并支持AI 和高性能数据分析(high performance data analytics,HPDA)、高阶有限元方法、图形分析、神经科学、量子化学、信号处理和许多其他问题领域中发生的较小矩阵计算。例如,在ECP CEED(https://ceed.exascaleproject.org/)项目中,MAGMA 批处理方法用于对许多分组(例如,批处理)的小型高强度GEMM(general matrix to matrix multiplication)进行拆分计算。
MAGMA还支持各种稀疏数据格式,包括压缩稀疏行格式(compressed sparse row,CSR)、ELL(ELLPACK)、SELL-P 等。目前该团队的工作重心放在GPU 硬件加速上。基准测试结果所示[29],MAGMA-sparse在性能方面可以与NVIDIA 稀疏矩阵库cuSPARSE 8.0 相竞争。
2.4 SLATE
SLATE(https://icl.utk.edu/slate/)[11,30]为当前和未来的分布式内存系统提供基本的稠密线性代数计算能力。SLATE 将提供现有的LAPACK 和ScaLAPACK功能,包括BLAS的并行实现、线性系统求解器、最小二乘法求解器以及奇异值和特征值求解器。在这方面,SLATE 将作为LAPACK 和ScaLAPACK 的替代品,LAPACK 和ScaLAPACK 经过20 年的运行,已经无法完全适应现代的复杂架构体系。
SLATE 的目标是为ECP(exascale computing project)应用提供稠密线性代数计算功能,如EXAALT(exascale atomistics for accuracy,length,and time)、计算化学软件NWChemEx、量子蒙特卡洛软件QMCPACK、从头计算量子化学软件GAMESS,以及其他软件库和框架,如FBSS。SLATE主要特点有:
(1)面向现代硬件体系设计,例如已经面世的E级计算机。
(2)通过依靠标准的计算组件(如BLAS 和LAPACK的供应商实现)和标准的并行编程技术(如MPI、OpenMP)或可移植的运行时系统(如PaRSEC)来保证可移植性。
(3)依靠直观的单程序多数据(single program/multiple data,SPMD)编程模型和一组简单的abstractions 来表示稠密矩阵和稠密矩阵运算,从而提高工作效率。
(4)通过使用C++语言的有用工具(例如模板以及函数和运算符的重载)来确保可维护性,并最大程度地减少代码膨胀。
3 稀疏线性代数解法器
稀疏线性代数对稀疏矩阵进行操作,即在线性方程组Ax=b中,A的矩阵元素主要为零,稀疏矩阵中零元素的比例被称为稀疏性。因此,它可以利用压缩数据结构来实现计算和内存效率,其中只存储非零值及其索引。系数矩阵A的稀疏性决定了两种类型的线性代数之间的一个基本区别,即稠密线性代数一般是受计算复杂度约束,而稀疏线性代数通常是受内存约束的。
目前有很多优秀的稀疏线性代数解法器。Anzt等人[31]介绍了ECP 项目在为E 级计算平台提供稀疏求解器方面的挑战、策略和进展。本章介绍了PETSc、Trilinos、Hypre、Ginkgo 及SuperLU/STRUMPACK 的功能和特点。
3.1 PETSc
PETSc(http://www.mcs.anl.gov/petsc/)是由美国阿贡国家实验室开发的可移植可扩展科学计算工具包。PETSc是通过MPI实现进程之间的通信,通过调用BLAS 实现数值计算。PETSc 包含线性代数方程解法器、非线性代数方程与无约束优化方程解法器、偏微分方程(partial differential equation,PDE)或常微分方程(ordinary differential equation,ODE)时间依赖方程解法器等,且提供与MATLAB、ESSL、ParMETIS(https://scicomp.ethz.ch/wiki/ParMETIS)等的接口。PETSc 可用于用C、C++、Fortran 和Python 编写的应用程序。PETSc 支持分布式内存、共享内存和异构CPU-GPU架构,以及任何混合架构。2015年和2016年“戈登·贝尔”奖(Gordon Bell Prize)的获奖应用均使用了PETSc。
为了更好地利用基于众核和GPU 的系统,并提供对E级系统的扩展性,PETSc团队近几年主要关注以下三点:(1)开发部分无矩阵的可扩展求解器;(2)减少同步算法,与带有同步点的求解器相比,可以扩展到更大的并发性;(3)所有核心数据结构的性能和数据结构优化。
将PETSc数值库扩展到E级系统的挑战有:(1)用于线性、非线性和ODE 求解器的传统基于稀疏矩阵的技术以及优化算法都受到内存带宽的限制;(2)任何需要在所有计算单元之间进行的同步(如,内积或范数)都会极大地影响解法器的可扩展性;(3)需要支持E级系统里的各种加速器,以及支持应用程序团队用于性能可移植性的编程模型。为了解决数值库的可扩展性问题,PETSc实现了新的求解器和数据结构,包括:延迟使用内积和范数结果的pipeline Krylov方法,允许归约(reduction)和其他计算的重叠;使用高阶方法的部分无矩阵求解器,具有高浮点-内存访问比率,并且具有良好的使用众核和GPU 系统的潜力;代数多重网格所需的稀疏矩阵-矩阵乘积的节点内优化,以更好地利用众核系统。
3.2 Trilinos
Trilinos(https://trilinos.github.io/)是Sandia 国 家实验室开发的用来解决大规模复杂科学计算问题的科学软件库的集合,尤其以线性求解器、非线性求解器、瞬态求解器、优化求解器和不确定性量化(uncertainty quantification,UQ)求解器而闻名,支持并行计算机上复杂的多物理场和多尺度工程应用程序。Trilinos最初是为“flat MPI”而设计的,但近年来节点并发性随着从多核到众核架构(例如GPU)的广泛采用而增长,Trilinos采用了两级并行模型。在顶层,对象(矩阵、向量)分布在MPI rank 中。分布由映射给出,映射是Petra对象模型中的一阶对象。
在Trilinos 中,求解器包括直接稀疏方法,如Amesos2软件中的稀疏LU/Cholesky,以及Belos中包含的迭代方法(主要是Krylov 方法)[32]。预处理程序包括稳态方法和不完全因式分解(Ifpack2)、区域分解方法和(不)完全因式分解(ShyLU),以及代数多重网格(MueLu)。最近几年,Trilinos 的主要关注点是在Belos 中开发以加速器为中心的迭代求解器;在MueLu中开发多线程和面向GPU加速的多重网格方法;在ShyLU 中开发基于Kokkos[33]的直接因式分解方法,如Basker[34]和Tacho[35];在Ifpack2 和ShyLU 中开发面向GPU加速的区域分解方法。
3.3 Hypre
Hypre(http://www.llnl.gov/casc/hypre)是由劳伦斯利弗莫尔国家实验室开发的软件包,为在大规模并行计算机上解决大型稀疏线性系统提供了高性能的预处理器和求解器。Hypre 特点之一是提供概念线性系统接口,其中包括结构化、半结构化和传统的线性代数系统接口。这些接口为用户提供了一种更自然的方式来描述其线性系统。Hypre 库提供非结构化和结构化多重网格求解器,在各种高性能计算机上表现出出色的可扩展性,例如Blue Gene 系统(非结构化求解器BoomerAMG 已扩展到125 万个MPI内核,总共有450万个硬件线程)[36]。Hypre已经被许多ECP 应用程序团队所使用,包括ExaAM、Subsurface、ExaWind、CEED等。
非结构化代数多重网格求解器BoomerAMG,它是Hypre 最常用的预处理器,包含启动和求解两部分。粗网格算子是通过三个矩阵相乘得到的,这导致粗网格矩阵中每行的非零元数增加,并且相邻进程的数量也随之增加。以前在分布式内存机器上实现最佳收敛和性能的插值策略不适合在GPU或类似架构上实现,且计算机体系结构上的通信和计算成本之间的差异越来越大,因此开发试图最小化通信与计算比率的算法非常重要。这对于具有最优O(N)计算复杂度的多重网格方法来说尤其困难。消除通信通常会降低收敛性,因此可能不会加快整体求解时间(或降低功耗)。但Hypre 团队已经在许多方法上取得了一些成功,包括:通过稀疏插值技术使三维可变系数扩散问题加速了10 倍以上[37];具有乘性多重网格收敛速率的高并发加性多重网格方法使三维非结构化Laplace问题的速度提高了2.5倍[38];用于减少粗网格耦合和通信的非Galerkin 方法使固定系数三维Laplace问题的速度提高了15%至400%[39]。
3.4 Ginkgo
Ginkgo(https://ginkgo-project.github.io/)为迭代求解稀疏线性系统提供了求解器、预处理器以及中心基本构件。它适用于多核和众核架构,主要是C++实现的,它提供了多种稀疏矩阵格式,例如COO(coordinate,坐标的形式)、CSR、ELL、HYBRID、SELLP。同时,它提供了不同格式之间的高性能转换程序。
Ginkgo 提供了多种迭代求解器,例如共轭梯度方法(conjugate gradient,CG)、灵活的共轭梯度方法(flexible conjugate gradient,FCG)、双共轭梯度方法(biconjugate gradient,BiCG)及其稳定版本(biconjugate gradient stabilized method,BiCGSTAB)、广义最小残差法(GMRES)等Krylov 子空间方法,还提供更通用的方法,如迭代更新方法(IR)。Ginkgo 还支持带不完全因式分解预条件的直接和迭代三角求解。基于内存访问器,Ginkgo团队部署了压缩基GMRES(compressed basis GMRES,CB-GMRES)求解器,该求解器通过以较低的精度存储Krylov基矢从而加速内存访问,且性能优于GMRES[40]。
Ginkgo 具有一些最先进的通用预处理器,如支持通过动态调整内存精度减少内存带宽压力的块Jacobi预条件[41],该版本通过动态调整内存精度来减少对内存带宽的压力,以满足数值要求,这种方法已被证明对具有块结构的问题非常有效[42]。Ginkgo 还具有高度并行的不完全因式分解预条件,如ParILU和ParILUT 预处理[43]、近似逆预条件(如不完全稀疏近似逆预处理)以及多重网格预条件。
由于稀疏算法在几乎所有的现代架构上都受到内存的限制,人们探索了各种策略来减轻对内存带宽的压力,如分层结构的稀疏数据格式压缩技术和混合精度算法。Ginkgo 解决了内存瓶颈问题,它采用模块化精度生态系统,将内存精度与算术精度格式解耦,只为算术操作保留全精度,并根据算法要求动态调整内存精度。Ginkgo还包含了最新的混合精度算法[41],这使得该库适用于各种科学应用。Ginkgo是超大规模软件开发工具包(xSDK,https://xsdk.info/)的一部分,是超大规模科学软件栈(E4S,https://e4s-project.github.io/)的一部分,并且已经集成到一些库中,如deal.II、MFEM和HyTeG。
3.5 SuperLU/STRUMPACK
稀疏分解和对应的求解算法(如与LU分解相关的三角求解)通常是多物理学和多尺度模拟的线性系统最稳健的算法选择。它们可以作为直接求解器被使用,例如作为多重网格算法中的粗网格求解器,或者作为迭代求解器的预处理子。SuperLU/STRUMPACK这两个求解器都是纯代数的,适用于各种各样的应用领域。
SuperLU(https://portal.nersc.gov/project/sparse/superlu/)是一个通用的库,用于直接求解大型稀疏非对称的线性方程组,已有超过20年的发展历史,它适应的体系架构从多核、分布式内存发展到最近的多核GPU 集群。该库是用C 语言编写的,可以从C 语言或Fortran程序中调用。它支持实数和复数数据类型,支持单精度和双精度计算。该库包含部分主元LU 分解以及通过向前和向后回代进行三角系统求解。LU 分解程序可以处理非方阵,但三角系统求解只针对方阵。SuperLU还包含预估条件数、计算相对向后误差等。SuperLU 有超过20 年的发展历史,从多核、分布式内存发展到最近的多核GPU集群,被能源部、工业界和学术界的众多应用所使用。尽管它们具有广泛的实用性,但传统因式分解算法的一个基本扩展障碍是,所需的flops 和内存与问题大小不是线性关系。
STRUMPACK(https://portal.nersc.gov/project/sparse/strumpack/)是一个提供线性代数程序和线性系统求解器的软件库,它于2015年首次发布,目前拥有许多能源部的用户。STRUMPACK用于稀疏和稠密秩结构的线性系统。STRUMPACK 使用multifrontal 算法实现稀疏LU 分解。他们在稀疏因子中的稠密块(frontal矩阵)中引入了数据稀疏性,使用了几种分层矩阵低秩压缩格式,包括分层半分离(hierarchically semi-separable,HSS)、分层非对角线低秩(hierarchically off-diagonal low rank,HODLR)和块低秩(block low rank,BLR)。除了秩结构压缩,STRUMPACK 稀疏求解器还支持使用ZFP库对因子进行压缩,这是一种针对浮点数据的通用压缩算法。这可以在指定的精度下使用,也可以使用无损压缩。
STRUMPACK的稀疏求解器也可以作为精确的直接求解器使用,在这种情况下,它的功能与SuperLU或Superlu_Dist 等类似。STRUMPACK 还提供预条件GMRES和BiCGStab迭代求解器。
4 数值线性代数核心技术进展
新一代数值线性代数算法,除了最大限度地提高速度和准确性外,最大限度地降低能耗也是一个重要考虑标准。这些优化技术包括:提高缓存局部性和向量化程度以最大化利用体系结构特征;深入理解科学应用的动态行为,并在必要时适当降低计算性能和数值精度以满足降低能效的目标;设计新的通信避免算法以减少节点间数据传输。为了利用好现代及未来的超级计算机,Dongarra等人[44]讨论了一些高效可行的优化方法。
4.1 性能可移植性
之前的超级计算机均采用NVIDIA GPU,但是最近几年AMD GPU和Intel GPU也陆续被一些超级计算机所采用,例如:Frontier 和EL Capitan 使用的是AMD GPU,Aurora 使用Intel GPU。表2 列出了主流数值线性代数解法器目前对各GPU 架构的支持情况。针对性能可移植性,目前采取的策略主要有:
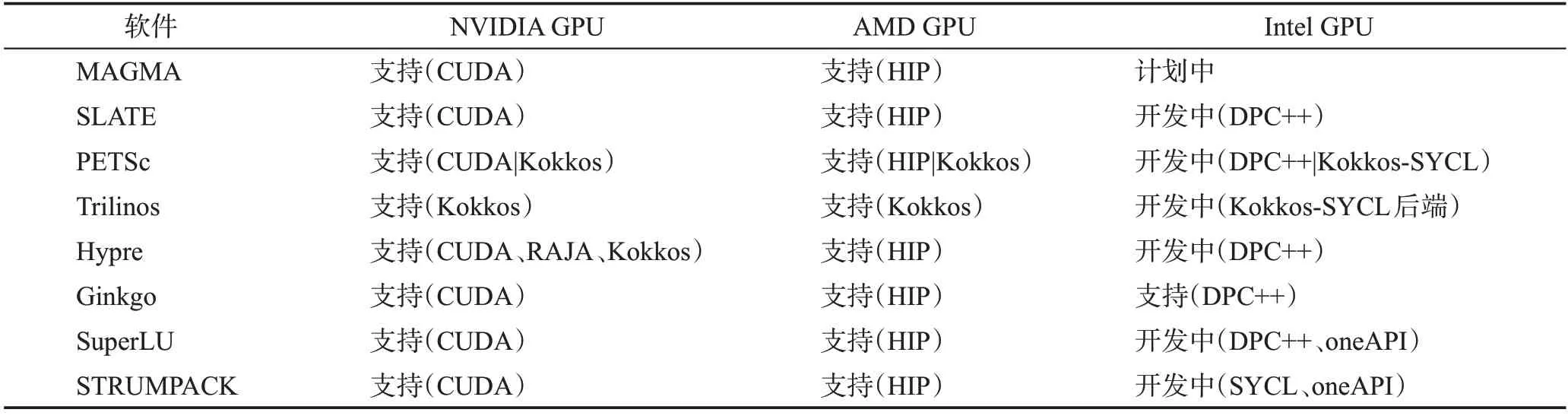
表2 对主流GPU架构支持的情况Table 2 Support for mainstream GPU architectures
(1)主要采用隔离影响性能的代码,编写CUDA、HIP、SYCL(https://www.khronos.org/sycl)后端;
(2)使用Kokkos和RAJA(https://github.com/LLNL/RAJA)作为主要可移植层;
(3)结合前面两种策略。
MAGMA 的最新版本是用于CUDA 和HIP 的MAGMA 2.7.1。MAGMA采用多种针对异构平台的优化方法,例如混合同步、动态任务调度及通信避免。MAGMA 使用混合方法,算法被拆分为不同粒度的任务,并且被分配到相应可用的硬件组件上进行计算。调度可以是静态的,也可以是动态的,通常在关键路径上安排的小型不可并行化任务都调度到CPU上进行计算,而更大的可并行化的任务(通常是3级BLAS)调度在GPU上进行计算。
SLATE 是建立 在MPI 和OpenMP 等标准以及NVIDIA CUDA和AMD HIP等行业标准解决方案之上的。与ECP Exa MPI 和OMPI-X 项目的合作是为了提高消息传递能力,而与ECP SOLLVE 项目的合作旨在改进多线程能力。SLATE 项目还包括为BLAS、LAPACK 以及batch BLAS 设计和实现C++API。在这些API 下,将调用高度优化的供应商库以实现最大性能,如Intel MKL、IBM ESSL、NVIDIA cuBLAS、AMD rocBLAS。
PETSc性能可移植性主要基于Kokkos和Kokkos Kernels,支持向量、矩阵和矩阵矩阵操作。PETSc/TAO中支持加速器的总体策略基于灵活性和关注点分离(separation of concerns),将用户编程语言和编程模型的数据指针包装在PETSc矢量和矩阵矢量对象中。这种方法使PETSc项目组能够将精力集中在向量、矩阵向量、矩阵矩阵和其他计算的kernels 上,而使用PETSc 的人员可以专注于他们的应用程序。PETSc提供多个后端,并支持AMD、英特尔和NVIDIA加速器。
Trilinos 依靠基于库的方法来实现可移植性,其中模版化分布式线性代数容器Tpetra 的底层基本都是基于Kokkos 实现。Kokkos 可以轻松地将Tpetra移植到新的计算机架构,并扩展其对并行计算内核和线程可扩展数据结构的使用。Tpetra有以下优点:(1)通过Kokkos 支持多核和众核架构;(2)模板化的标量类型允许轻松切换精度,包括混合精度;(3)64位整数和指针支持非常大的计算规模。
Hypre 库之前使用MPI/OpenMP 且不支持GPU。由于当今计算机体系架构以异构为主,Hypre团队近几年开始研究使Hypre 能够利用GPU 的各种方案,如使用CUDA、OpenMP 4.5、RAJA 和Kokkos。他们将后三种方案限制在结构化接口和求解器上,使用了BoxLoops 循环宏。对非结构化接口采用了模块化的方法,这种方法依赖于重组求解器组件以使用较小的kernels,这些kernels 的CUDA 版本正在实现中。由于HIP与CUDA相似,移植到AMD GPU 上是相当直接的。他们正在研究使用供应商提供的从CUDA到SYCL的转换工具,将结构化和非结构化的求解器移植到带有Intel GPU的E级计算机上。
Ginkgo 在线性代数求解器、预条件求解器和矩阵格式方面具有可扩展性。它主要是基于C++(C++11标准)实现,利用各种C++功能(如数据抽象、泛型编程和自动内存管理)来提高库的性能,同时保持易用性和可维护性。为了最大限度地提高兼容性和可扩展性,Ginkgo 将包含算法的core 与特定架构的后端分开。使用特定架构的“执行器”,可以根据硬件架构和并行化策略的变化而添加、删除或修改后端。Ginkgo 支持CUDA(用于NVIDIA GPU)、HIP(用于AMD GPU)和OpenMP(用于通用多核处理器,如英特尔、AMD或ARM的处理器)。Ginkgo与硬件供应商的库(如hipSPARSE 和cuSPARSE)相比具有竞争力。
STRUMPACK使用混合MPI+OpenMP的并行方式。STRUMPACK的求解器和预处理器采用多层次的并行性:稀疏矩阵消去树的并发性、HSS 层次的并发性和BLAS/(Sca)LAPACK程序的并发性。STRUMPACK 中的多层次并行性使得代码移植到GPU 架构上非常具有挑战性。STRUMPACK目前仅支持稀疏直接求解器中的GPU 加速,预条件和秩结构化求解器尚未支持GPU加速。
4.2 混合精度
多年来,科学计算一直在支持IEEE 1985算术标准的硬件上进行单精度(fp32)或双精度(fp64)运算。2008 年,修订后的IEEE 标准引入了半精度(fp16)和四倍精度(fp128)格式。半精度仅用于存储,但现在一些硬件支持将其用于计算。除了IBM z13系统,四倍精度仅在软件中可用。
期望浮点运算的成本与操作数的位数大致成正比,因此从双精度到单精度或从单精度到半精度应该会有2 倍加速。较低精度的数据还可以降低存储要求和数据移动成本。NVIDIA 的Volta 和Turing架构包含tensor cores,可以执行块FMA(fused multiplyadd)运算。Tensor Cores 支持混合精度计算,动态调整计算以加快吞吐量,同时保持精度。
2019 年,LINPACK 基准和HPL 的提出者Dongarra 对LINPACK 进行扩展,即HPL-AI(https://icl.utk.edu/hpl-ai),以评估超级计算机在混合精度计算上的性能。HPL-AI在矩阵求解过程中放弃双精度计算的要求,可以利用已有的和即将推出的AI 设备来加速整个求解过程。同时使用IR 算法,恢复在低精度运算中损失的精度。
Abdelfattah等人[45]总结了ECP xSDK-multiprecision开发和部署的混合精度技术进展。
PLASMA为求解一般线性方程组和对称正定矩阵方程组实现了混合精度例程[9]。PLASMA 采用和LAPACK 一样的混合精度算法。这些算法基于在迭代更新(IR)过程中以单精度对矩阵进行因式分解,并在迭代更新过程中采用双精度。
MAGMA 库支持多个精度,支持基于LU、Cholesky 和QR 分解的混合精度IR 算法,其中采用fp16或fp32作为低精度运算。
SLATE 中实现了两个混合精度求解器[46]:基于LU 分解的gesvMixed()例程和基于Cholesky 分解的posvMixed()例程。这些例程将低精度和高精度作为模板参数。因式分解在低精度下进行,迭代更新在高精度下进行。
Ginkgo 采用三种机制实现混合精度算法的性能:(1)Ginkgo 具有封装动态压缩的内存访问器,用于将内存精度与算术精度解耦。这会加快内存约束算法的性能,这些算法可以容忍内存操作中的一些信息丢失。(2)Ginkgo 允许不同精度格式存储的向量不需要进行显式格式转换即可进行线性操作。(3)Ginkgo 包含许多有效的混合和多精度算法,如混合精度稀疏近似逆预处理或CB-GMRES方法。
Trilinos、Kokkos Core 和Kokkos Kernels 最近加入了一些混合精度和多精度功能。主要包括:(1)在Kokkos Core 中增加了半精度功能。这使得ECP 应用程序和软件技术项目可以使用半精度的可移植算术特征实现,并使用半精度类型的Kokkos 编程模型范式。出于性能的考虑,Kokkos也支持对某些操作使用更高的精度。(2)支持半精度稀疏/稠密线性代数。(3)Trilinos在其线性求解器中具有单精度MueLu(多重网格)和IfPack2(基于因式分解的)预处理能力。
PETSc 中的混合精度方法侧重于为供应商代数库(如cuBLAS/cuSPARSE、rocBLAS/roc-SPARSE)和其他支持混合精度的库(如Ginkgo)开发抽象层。PETSc团队拟计划在PETSc 4中增加多精度功能。
Hypre 库目前可以构建成三种精度(单精度、双精度和四倍精度)。精度类型的选择由用户在构建时通过设置选项--enable-来指定
4.3 通信避免算法
通过提高数据可重用性并在数据位于cache 等上层存储中时对数据执行尽可能多的计算,可以最大限度地减少低级别存储的数据传输并提高性能。
Barron 等人[47]在1960 年首次尝试减少稠密线性代数中的通信,他们使用EDSAC 2 计算机通过高斯消去法求解线性方程组。他们采用块LU分解,这种块分解是在大多数稠密线性代数库中(如LAPACK、ScaLAPACK、PLASMA)实现的算法的基础。近年来,为了减少甚至最小化数值线性代数中的通信,人们引入了一种不同的方法,即依靠不同的方式来计算相同的代数运算。例如,矩阵的LU分解是通过使用不同的选主元策略而不是使用列/行选主元来计算的,同时保持数值的稳定性。这些算法被称为通信避免(communication-avoiding,CA)的算法。ECP PEEKS和Clover项目最近支持的算法重点也是通信避免方法。
SLATE[48]中使用Grigori 等设计的tournament 选主元LU方法(通信避免的LU分解,CALU)[49]。该方法已经被证实是有效的[50]。CALU 的主要思想是通过执行冗余算术运算来减少panel分解期间交换的消息数量。CALU 和经典LU(即列/行选主元LU)之间的主要区别在于panel 分解。在LU 中,处理器需要同步panel的每一列,而在CALU中,处理器只需要同步panel的每个列块。
虽然Krylov 方法具有良好的收敛性,但它们通常依赖于全局内积(或正交化),这对于大规模的计算体系可能很昂贵。Trilinos 中Belos 软件包现在支持single-reduce、pipelined 和s-step(CA)求解器[31],这是减少通信和同步的三种不同方式。single-reduce方法通过将两个或更多的all-reduce 操作合并为一个,将每次迭代中调用全局(all-)reduce 的数量减少到只有一个。pipelined方法将全局通信、局部通信和计算重叠在一起。s-step方法每s步通信一次,其中s是一个小整数。在CA-GMRES 中,正交化步骤被更有效的块正交化所取代。代价是需要更多的内存来存储“ghost”数据。未来的一个潜在改进是采用“矩阵幂kernel”来计算Krylov基。
为了降低算术复杂度,SuperLU团队开发了一种新型的通信避免的因式分解和三角矩阵求解方法[51],其中MPI 进程被布置为三维进程网格,沿进程网格的第三个维度选择性复制数据,用少量增加的内存换取大大减少的每个进程上的通信。由于算术强度较低和任务依赖性较高,求解阶段比因式分解更具挑战性。他们引入了两种主要技术来减少同步的数量:第一种技术使用基于异步二叉树的通信方案,通过非阻塞的MPI函数实现,在4 000多个核心上实现了4倍的改进;第二种技术利用one-sided MPI通信功能来实现无同步任务队列,允许更多的通信和计算重叠,从而在4 000多个核心上获得额外的2倍改进[52]。
5 总结与展望
为了充分发挥现代超级计算机的计算性能,提升应用计算规模,降低能耗成本,主流稠密及稀疏线性代数解法器面向高性能计算体系架构进行了许多功能及性能方面的优化。本文对主流线性代数解法器进行了总结。针对新一代超级计算架构,解法器的发展主要有两类表现:一类是新开发的数值线性代数软件包,如SLATE 和Ginkgo 明确针对新型节点架构从头设计实现新算法;另一类是已经存在的数值线性代数库,如Hypre、PETSc和Trilinos等,正在模块化集成、调整适配式发展。
面向现代计算架构,数值线性代数解法器也需要进行优化,这些优化技术包括:隔离异构计算模块和设计新的统一编程框架,以实现软件的性能可移植性;利用混合精度方法提升数值计算和数据存储的性能水平;发展并实现通信避免算法,避免或减少效率低下的大规模数据通信。目前各解法器在这些方面都取得了阶段性进展,但还需要根据E级计算的特点继续完善。比如,对于硬件驱动的算法设计,了解到该行业将继续生产针对其他市场(如ML应用程序)的加速器。在不久的将来,GPU加速器(NVIDIA、AMD/ATI、Intel)和具有宽矢量扩展的多核处理器(如ARM SVE和Intel的AVX512)将继续占据主导地位。因此,还需要加大力度设计及实现适配这些加速器的数值线性代数算法。
面对我国E级超级计算机的特定体系架构,国家也推出一些高性能数值线性代数解法器,从而为顶层应用性能发挥提供了基础支撑。目前我国高性能数值线性代数解法器要更好地发展,还需从几个方面努力:首先,加强与应用领域专家合作,实现面向应用需求的解法器性能优化和功能扩充,特别是大规模计算应用驱动的软件算法发展;其次,加强与国内计算数学领域专家合作,将最新的优秀算法集成到解法器里;最后,加强与具体超级计算机体系架构适配,充分挖掘硬件性能,实现面向特定体系结构的解法器性能优化和功能扩充。
