某型号转向机上管柱仿真研究

2023-10-29郝佳伟刘杰赵鸿博孙通刑祚祥

农业装备与车辆工程 2023年10期

郝佳伟，刘杰，赵鸿博，孙通，刑祚祥

（1.201800 上海市博世华域转向系统有限公司；2.200093 上海市上海理工大学机械工程学院）

0 引言

转向系统是汽车最重要的部件之一，对安全性和驾驶舒适性有直接的影响。转向系统一直受到汽车设计人员和生产制造商的广泛关注，相关研究在过去几十年中取得了重要进展。汽车上管柱结构作为汽车转向系统的核心部件，连接了方向盘和车身横梁，对汽车的行驶安全具有至关重要的作用。

近年来，学者们对转向机系统的研究主要集中在结构设计、仿真优化以及控制等方面。Bu 等[1]为六轮电动汽车设计了一种具有较高灵活性的独立转向系统；李谷楠等[2]详细阐述了管柱式助力转向系统的结构；徐畅[3]通过ANSYS 软件对转向机的核心结构进行了实际工况的仿真分析和优化；李文中等[4]针对转向支架进行了强度分析，并验证了疲劳分析结果与实际寿命；Gao 等[5]通过数值方法研究了转向系统刚度和阻尼对不同类型操作频率下车辆瞬态特性的影响；米峻男[6]设计一种双余度线控系统，提高了转向系统的安全可靠性；此外，周全[7]针对齿轮齿条式动力转向机进行了故障预测，为转向机的寿命管理提供了重要的参考；Fu 等[8]提出一种基于风险优先级数的驱动系统容错定量评价方法，并通过多体仿真研究了典型的失效模式的影响；Guo 等[9]针对液压转向系统高耗能等问题，提出了一种基于闭环泵控的电动轮式转载机电液流量匹配转向系统，通过实验验证该转向系统能耗降低22.8%。以上研究更多关注转向控制，针对上管柱的结构频率分析很少涉及。

本文以简化的转向系统上管柱结构模型为例，采用ABAQUS 有限元仿真软件，对其结构频率及进行了仿真分析和试验验证，并研究了轴承支承刚度值对系统固有频率的影响。

1 转向机系统模型

1.1 三维模型

采用CERO 三维软件建立了如图1 所示的转向系统模型，其由上管柱结构、中间轴、下管柱3部分组成。其中上管柱结构主要由上管柱和驱动单元组成，其三维模型如图2 所示。

图2 上管柱结构三维模型Fig.2 3D model of upper tube column structure

1.2 有限元模型

（1）动力学模型。由于上管柱结构太过复杂，工程实际中常进行简化之后搭建有限元模型，建模后的动力学方程为

式中：M——质量矩阵；K——刚度矩阵；C——阻尼矩阵；x——系统的位移响应量；F——激振力。

（2）有限元模型建立。对上管柱结构进行分析时，由于上管柱结构以及连接关系复杂，在充分考虑实际工况的情况下，将有限元模型进行简化。模型中的输入轴、输出轴、扭杆等都采用beam 单元进行等效代替，轴承采用Wire 进行连接，方向盘和电机采用集中质量单元mass 进行等效代替，简化后的有限元模型如图3 所示。其中钣金件的材料为结构钢，铸造件的材料为铸铝，具体属性如表1 所示。

表1 结构的材料属性Tab.1 Material properties of the structure

图3 上管柱有限元模型Fig.3 Finite element model of upper tube column

2 结果分析

2.1 模态分析

假设系统在分析时不受到阻尼的影响，求解对系统的固有频率。当系统没有阻尼力时，此时系统的运动方程为

求得位移响应为

将式（3）代入式（2），得到

由于系统在振动过程中的振幅不全为0，所以

通过将方向盘总成2.56 kg 的质量施加在方向盘质心点处，采用ABAQUS 仿真软件中Block Lanczos 得到上管柱系统的前6 阶模态振型图，如图4 所示。可见，随着模态阶数增大，上管柱系统振动幅度越大。1 阶模态时系统基本没有发生变化；2 阶模态时系统在水平方向上振动；3 阶模态时系统在垂直方向上振动；4 阶模态时系统在垂直方向上振动；5 阶模态时系统在水平方向上振动；6 阶模态时系统在水平方向上振动。

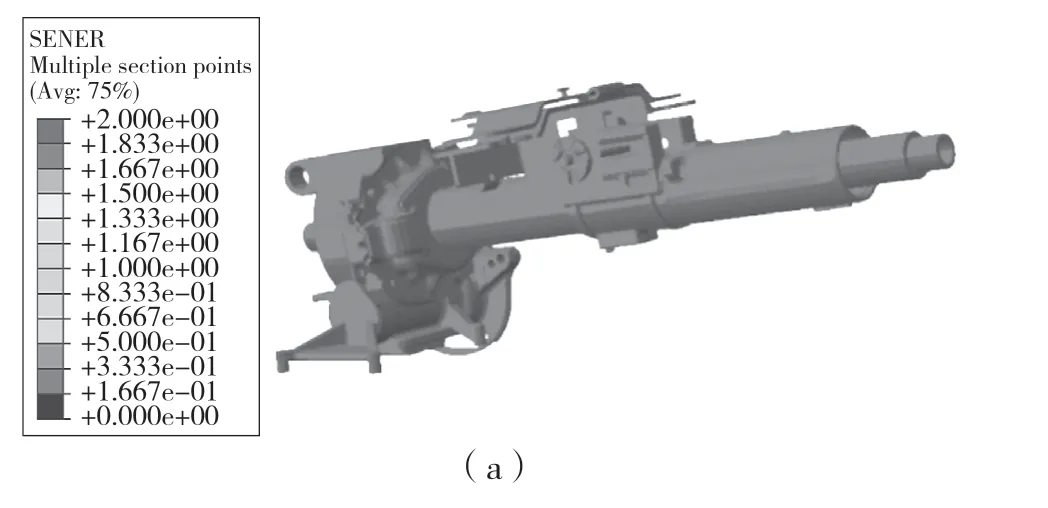
图4 系统前6 阶振型图Fig.4 The first six orders of system vibration diagram

上管柱结构前6 阶固有频率如表2 所示，由表2 可知，在第4 阶模态时系统固有频率迅速变大，因此在实际工况中为防止汽车发生共振，需要避开系统的固有频率。

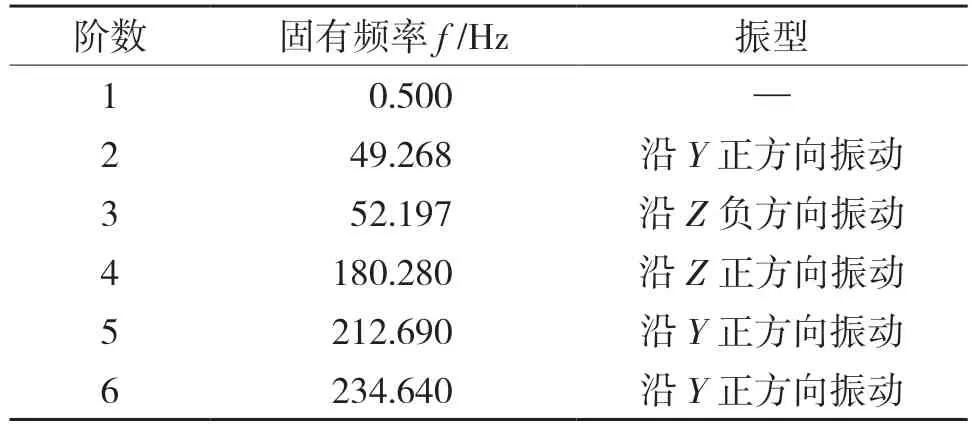
表2 上管柱结构前6 阶固有频率值Tab.2 The first six orders of inherent frequency values of upper tube column structure

2.2 试验结果验证

将转向管柱固定于频率试验台，管柱处于角度调节最下、长度调节最长位置，各附件固定夹紧，装上实车用方向盘或等质量配重块，配重块重心位置同方向盘，测定固有频率。图5、图6 分别为垂直和水平方向上的频谱图，垂直方向和水平方向的试验频率均为51 Hz。对比仿真结果可得，水平和垂直方向的误差分别为3%和2%，满足试验要求。

图5 垂直方向上试验频谱图Fig.5 Experimental spectrum in vertical direction

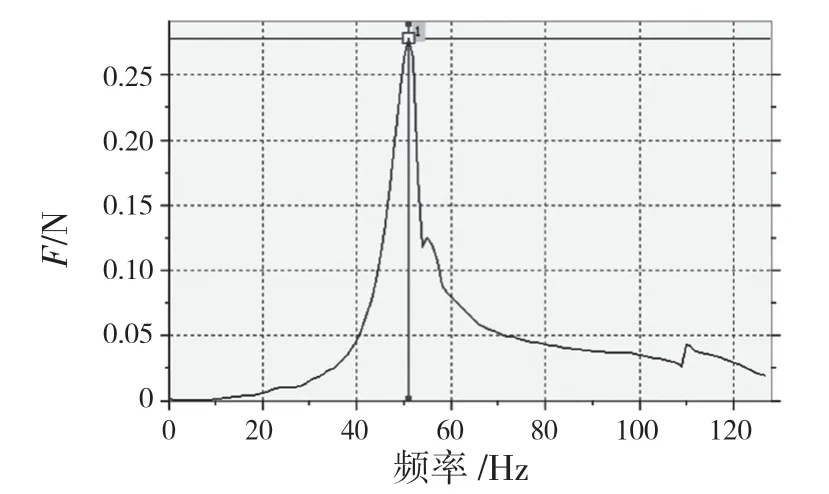
图6 水平方向上试验频谱图Fig.6 Experimental spectrogram in horizontal direction

3 轴承刚度对系统固有频率的影响

实车管柱连接了方向盘和车身横梁，串联系统具有更大的柔性及更大的集中质量，故系统固有频率更低，在路面或发动机激励下，最低阶模态容易被触发，产生共振，从而导致转向系统发生严重失效，甚至会导致车毁人亡。

由于上管柱各轴系通过支撑轴承进行连接，导致支撑轴承的刚度必然会对系统的固有频率产生较大影响。改变上轴承的支承刚度研究系统固有频率的变化，其中系统的固有频率随支承刚度值的变化如图7 所示。由图7 可见，随着支承刚度增大，第1 阶固有频率基本不发生变化；第2 阶到第6 阶固有频率在支承刚度为200～3 000 N/mm 的范围内快速增大；当支承刚度超过3 000 N/mm 时，系统的固有频率基本不发生变化，保持一个恒定值。因此在选取支承刚度值时需避开对固有频率影响较大的区间。