基于ANSYS 的四旋翼无人机结构拓扑优化方法

蔡文杰

（200093 上海市 上海理工大学 机械工程学院）

0 引言

无人机发展于20 世纪90 年代，具有体积较小、高机动性、低成本等优点，在军事和民用2 个方面皆有广泛应用[1]。多旋翼无人机按照轴数可分为三轴、四轴、六轴、八轴等。其中四轴旋翼无人机较多，因其结构相对简单且不需要反扭装置[2]。四旋翼无人机主要由控制器、机体机构、数据通信链、动力系统4 部分组成。对机身结构的研究主要是对其静力学进行强度校核，再根据分析结果修改设计，如此反复。目前，对无人机的研究主要集中于飞行控制算法，在设计流程中加入拓扑优化设计的较少[3]。

本文以四旋翼无人机机架为研究对象，建立了初始几何模型，对其进行静力学分析。基于Workbench 对机架进行拓扑优化，在拓扑结果上对初始模型进行重构并且二次验证性能；在无人机机架变形较小的情况下，对机身进行了轻量化设计。研究结果为实际生产制造无人机机架提供一种新的思路，为实现低成本、轻量化的结构设计提供一种新的途径。

1 拓扑理论与数学模型

1.1 拓扑优化理论

拓扑优化是结构优化的一种，其主要根据载荷情况、约束条件和性能指标，在规定的区域内对材料分布进行优化。拓扑方法主要有均匀化方法、变密度法、渐进结构优化法、水平集方法、可变形孔洞法等。本文采用变密度法连续体拓扑优化，其优化设计变量为单元相对密度。在离散型优化问题中，单元优化设计变量取值为0 或1[4]，由于单元相对密度的引用，单元优化设计变量的取值在区间[0,1]连续，从而转化了离散型优化和连续型优化问题[5]。

1.2 数学模型

在变密度法优化的过程中，SIMP 插值模型法目前使用较为普遍，其数学表达式为

在SIMP 材料插值模型法基础上，连续体拓扑优化问题数学模型为

式中：C——目标函数，结构的总体柔度；F——力向量；U——位移列阵；K——结构总刚度矩阵；V0——整个设计域的初始体积；f——优化体积比；V——优化后的结构体积；xi——设计变量是单元相对密度；xmin、xmax——单元相对密度的最小极限值和最大极限值；uiT——单元位移向量；n——结构离散单元总数[6]。

2 静力学仿真及结果分析

2.1 初始结构设计

四旋翼无人机的结构设计需要具备质量轻、强度高、布局合理等性能要求。除了4 个旋翼的动力系统之外，无人机还包含了控制、通讯、能源系统。在充分考虑其他系统的空间位置、工艺要求下，确定了无人机机架的初始模型，如图1 所示。4 处旋翼对称分布在机架的前后、左右方向且处于同一高度平面，4 个旋翼结构相同、半径相等。机架中间螺纹孔用于安装飞行控制模块等外部设备。该无人机机身整体采用增材制造，其材料属性见表1。

表1 某四旋翼无人机机架材料属性表Tab.1 Rack material properties of a quadrotor UAV

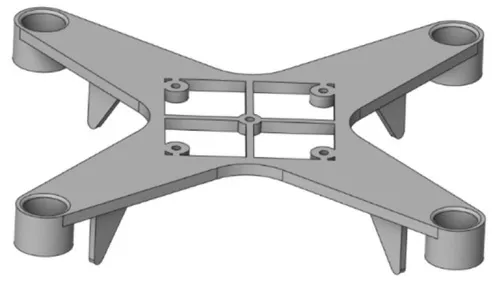
图1 无人机机架模型Fig.1 UAV rack model

2.2 静力学分析

在ANSYS Workbench中新建静力学分析模块。导入建立的机架模型，并进行网格划分，网格大小设置为1.5 mm，如图2 所示。在对无人机这类完全无约束的模型进行静力学分析时，通常使用惯性释放边界条件对机身进行约束[7]。

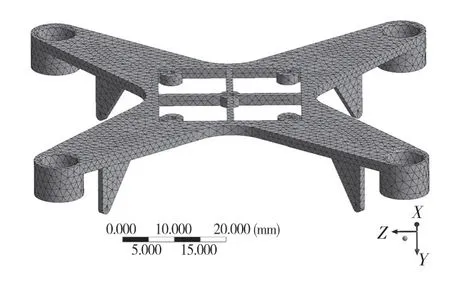
图2 无人机机架网格划分图Fig.2 UAV rack grid partition diagram

四旋翼无人机飞行原理是电机调节4 个旋翼的转速，实现4 个旋翼升力的变化，从而调节飞行器的姿态。机身一共有4 处电机，当无人机平衡飞行时，1、4 号电机顺时针旋转，2、3 号电机逆时针旋转，陀螺效应与空气动力扭矩效应均被抵消。四旋翼无人机机架主要受力为螺旋翼的拉力、自身重力和飞行时的风阻，具体受力分析如图3 所示。

图3 无人机受力分析图Fig.3 Force analysis diagram of UAV

本文主要对无风工况下无人机在空中悬停状态进行研究分析。无人机空中悬停时，4 个旋翼的升力和机身自身重力需要满足静力平衡条件。

式中：G——重力；F——机翼升力；M——无人机飞行重量；g——重力加速度。

无人机载荷M=1 500g，取g=9.806 6，由式（7）得重力G=14.708 N。根据静力平衡条件，升力F=14.708 N。进行力学仿真，结果如图4 所示。由图4（a）可知，最大变形位置出现在机翼最外端旋翼处，最大总变形为1.928 9 mm；由图4（b）可知，最大应变位置在机架中部螺丝固定处，最大等效应变为0.011 8；由图4（c）可知，最大应力位置出现在机架中间处，最大等效应力为30.041 8 MPa。对于塑性材料的许用应力[σs]=σs/ns（ns=1.2～2.0），取ns=2.0，则[σs]=40 MPa，小于机身材料的许用强度，因此该无人机机架满足静强度要求。由于四旋翼无人机机臂对称分布，弯曲变形产生的旋翼平面分力可以抵消。故1.928 9 mm 的变形量完全不影响无人机正常使用。

图4 机架静力学分析结果云图Fig.4 Frame statics analysis result cloud image

3 拓扑优化及模型重构

按照体积约束对机架进行拓扑优化，保留原体积的62%，获得拓扑云图，如图5 所示。4 个旋翼安装孔和机架中间几个螺纹孔处为非优化区域。机身和支脚部分均被优化成镂空状。

图5 机架结构拓扑优化结果云图Fig.5 Cloud image of topology optimization results of rack structure

拓扑后的模型是由诸多小面片拼接而成的实体，为便于后续模型分析和产品的美观性，在充分解读拓扑结果的前提下，采用Spaceclaim 的建模方式重建拓扑后的机架构型。如图6 所示，重构后的模型对称镂空了4 处机翼部分，处理了支脚和机架中间部分的拓扑结果边缘，使得模型更加简洁美观。

图6 重构的无人机机架结构Fig.6 Reconstructed UAV rack structure

4 二次静力学验证

为更好地验证重构后无人机机架合理性与力学性能，对新机架进行静力学分析。约束条件和载荷的设置均与拓扑前的模型静力学分析相同，计算得到的云图如图7 所示。

图7 新型机架静力分析云图Fig.7 Static analysis diagram of new frame

由总变形云图可知，新型机架最大变形量为1.843 5 mm，最大应力为17.806 MPa。新型结构的应力分布合理，最大应力出现在机翼与机身连接处且小于材料许用应力40 MPa，故新型机架满足刚度和强度要求。

5 结语

本文对某型消费级四旋翼无人机机架进行设计，并使用Spaceclaim 进行模型的建立。

（1）分析了无人机在无风工况下空中悬停时的受力情况，基于ANSYS Worbench 对机架的强度和刚度进行研究，机身所受到的最大等效应力为30.041 8 MPa，小于许用应力40 MPa，最大总变形为1.928 9 mm，对无人机使用影响较小，符合刚度条件。

（2）在此静力学基础上，基于ANSYS 拓扑优化模块，以最小体积为约束，最小质量为优化目标，对无人机机架进行拓扑优化。

（3）重构了拓扑结果，设计了新型机架，并对其进行静力学分析与动力学分析，二次验证机架的力学性能。

（4）新机架静力学分析结果表明：总变形量较小，最大等效应力小于材料的许用应力值。

新型无人机机架在满足性能需求的情况下，质量减少了41%，为无人机机架的结构设计提供一种新的设计思路。