基于改进蚁群算法的无人机三维路径规划

唐熙，王海宝，罗强

（404120 重庆市 重庆三峡学院 智能山地农机技术研究中心）

0 引言

无人机的路径规划算法是实现无人机自主飞行的重要研究方向。与传统地面机器人相比，无人机在路径规划中不仅要考虑时间和动力学的约束，还要考虑地形可能导致的碰撞[1]。因此学者们提出了许多三维环境下的路径规划方法，如人工势场法[2]、萤火虫算法[3]、RRT 算法[4]等。

蚁群算法是模拟蚂蚁觅食提出的一种算法，被广泛应用于解决旅行商问题[5]。Huang 等[6]考虑到无人机在路径规划时的静态威胁和动态威胁，在蚁群算法的基础上为障碍物添加排斥力场，并将斥力作为性能考察指标，改进后的算法能生成更加光滑的低成本路径；Zhang 等[7]利用插值法对地图进行栅格化处理，根据坡度阈值将三维地图转化为二维地图，利用并行技术加快蚁群算法；袁梦顺等[8]通过将人工势场法与状态转移策略进行融合，设置了双精英蚂蚁策略，提高了算法的全局搜索能力；刘雨青等[9]利用Dijkstra 算法进行信息素初始化，根据不同路径点能量消耗的差异来改进启发式函数，并采用贝塞尔曲线进行平滑处理，规划出的路径较传统蚁群算法能耗比降低了20%；王飞等[10]构造了新的启发函数，利用优质蚂蚁更新策略，自适应调整信息素挥发因子，比传统蚁群算法路径长度减少10%，迭代次数减少了40%左右，但是时间是传统蚁群算法的2 倍。

本文在现有蚁群算法的基础上以算法运行时间和最优路径长度为优化目标，采用改变搜索窗口大小的方式，根据无人机工作的最优高度范围改进启发式函数，通过2 组实验对本文改进算法与蚁群算法、王飞等[10]的算法（下文称算法W）进行比较，并得出结论。

1 三维模型建立

1.1 三维环境建模

首先以A为坐标原点建立一个ABCD-EFGH三维空间坐标系，其中无人机横向移动的方向为X轴，纵向移动的方向为Y轴，垂直移动方向为Z轴，沿X轴方向对AE进行K次等分，即可获得K+1 个平面，如图1 所示。利用地形高程信息中的横纵坐标与XY轴坐标对应，将高度信息存储在如式（1）所示矩阵T 中，则地形高度的顶点在坐标系中可以用（X，Y，T[m，n]）表示，连接相邻坐标即可表示整个地图的地形。

图1 三维模型Fig.1 Three-dimensional model

1.2 搜索模式

进行路径搜索时采取节点前进方式。无人机起飞点为Us，目标点为Ue，沿着X轴方向前进。从起始点所在平面K1开始，探索在K2平面可行区域内最优的下一节点位置，以此往复，总共探索K个平面。无人机在一定时间内的最大横移和最大纵移动为Ymax和Zmax，则无人机的搜索范围为（2Ymax+1）×（2Zmax+1）。搜索范围的大小对算法的运行时间有极大影响，减小搜索范围可以缩短蚁群算法运行时间，但搜索范围太小会导致蚁群算法陷入局部最优。传统蚁群算法搜索范围是一个固定值，缺乏灵活性，本文采用动态调整的方法。开始时，让无人机在一个较大的范围内搜索，在距离目标点一定范围内后，减小搜索范围（如图2 所示），加快算法运行时间，使整体算法性能达到最优。

图2 搜索模式Fig.2 Search mode

1.3 距离计算公式

在三维空间中，（xi，yi，zi）是蚂蚁当前的坐标，（xj，yj，zj）是下一点的坐标，（xe，ye，ze）为目标点的坐标。

蚂蚁从当前点到下一点距离

蚂蚁从当前点到目标点距离

2 改进蚁群算法

2.1 启发式函数改进

启发式函数是蚁群算法的核心，设计一个符合当前模型的启发式函数能提高蚁群算法的效率。蚂蚁m从当前节点到下一个目标点会依据路径上的信息素值和启发式信息计算状态转移概率[11]，其表达式为

式中：α——信息素启发因子；β——期望启发因子；ηij——启发式信息函数；τij——信息素函数。

启发式信息函数为

式中：M——距离系数，用于调整距离在启发式函数中的权重。

传统蚁群算法仅考虑与下一节点的距离，这样容易导致蚁群陷入局部最优。本文采用当前节点与下一节点和目标点的距离来引导蚂蚁选择距离目标点更近的下一节点，促使其向最优路径方向前进。

无人机在空中飞行也会受到地形的影响，如低空突防[12]、植保作业[13]会跟随地形进行飞行。之前的三维蚁群算法只是将高度作为一个安全状态看待，无人机飞行高度大于地形高度即为安全，反之为不可飞行区域。但是在无人机实际使用过程中，会存在一个最适工作高度，通过这一特性设置高度适应函数Sij，让无人机在执行任务过程中在最适高度飞行，以保证无人机有更好的作业条件，具体表达式为

式中：Fmin——安全状态下的最小离地高度；Wmax、Wmin——无人机最适飞行高度的最大值和最小值；Ti——当前位置的地形高度；dz——飞行高度。

2.2 初始信息素优化

蚁群算法在初期的搜索是随机的，初始化的信息素值对其有很大的影响。普通蚁群算法初始化信息素值是开始时设置一个统一的值。统一的信息素值会影响算法的收敛速度，为解决这一问题，在沿起始点到目标点的直线距离范围内的空间设置初始有利区域，该区域中初始信息素值高于其他区域的信息素初始值，表达式为

式中：τ0——信息数初始值；dse——起始点到终点的距离；P——dse上在无人机搜索范围内的点集合。

沿初始点到目标点设置不均匀的信息素分布[14]，有利于引导蚂蚁朝着目标点的方向前进，加快收敛速度。

2.3 精英蚁群信息素更新

信息素更新包括信息素挥发和信息素增强。信息素挥发有利于探索未知区域，避免陷入局部最优，信息素增强是增加路径上的信息素值，加快收敛速度。当蚂蚁在完成节点间探索后，当前节点的信息素会按照设置的信息素衰减系数ζ进行挥发，更新公式为

当蚂蚁完成一条路径的探索后会将本次路径长度与整个蚁群的最短路径进行比较，选出最短路径，在该路径上进行信息素增强，增大后续蚂蚁选择该路径的概率，采用蚁周模型更新信息素，更新公式为

式中：length(m)——第m只蚂蚁经过的路径长度；ρ——信息素系数；N——信息素常数。

为防止信息素过小，收敛速度慢，信息素过大，陷入局部最优，限定τij∈[τmin,τmax]。

2.4 改进算法流程

算法实现步骤：

（1）初始环境建模，设定起始点，目标点，设置蚁群数量，最大迭代次数等参数；

（2）信息素的初始化，根据式（8）计算初始值，并进行不均匀的信息素分配；

（3）蚁群探索。探索路径，根据状态转移概率式（4）求得下一节点，并按照式（9）进行挥发，直到探索完所有节点；

（4）判断蚁群是否完成路径探索，是进行步骤5，否返回步骤3，直到蚁群完成探索；

（5）对所有到达目标点的蚂蚁走过的路径进行信息素更新，并按照式（10）、式（11）增加最短路径各节点的信息素；

（6）判断蚁群的迭代次数是否达到设定值，是进行步骤7，否进行步骤2，直到完成迭代；

（7）输出最优路径长度，算法结束。

3 仿真与分析

算法运行环境为：处理器为AMD Ryzen 5800X，内存16 GB，MATLAB R2021a，采用本文改进蚁群算法、算法W 和传统蚁群算法进行对比实验，每种算法进行20 次实验，随机抽取其中5组作为最终结果，并选择出路径最短的一组对比其迭代次数。蚁群初始参数设置如表1 所示。

表1 蚁群初始参数Tab.1 Initial parameters of ant colony

3.1 实验1

随机生成一个20 km×20 km×2 km 的栅格地图，设置起飞点为（1，11，3），目标点为（21，10，5）。传统蚁群算法、算法W 和本文改进算法的实验结果分别如图3—图5 所示，3 种算法最优路径长度如图6 所示。实验结果见表2。

图3 蚁群算法Fig.3 Ant colony algorithm

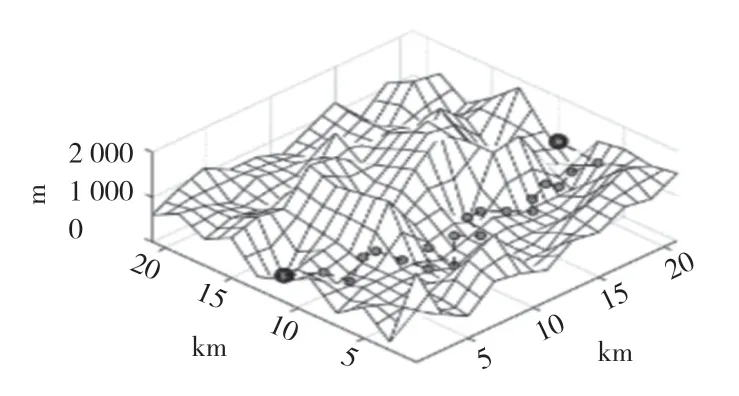
图4 算法WFig.4 Algorithm W

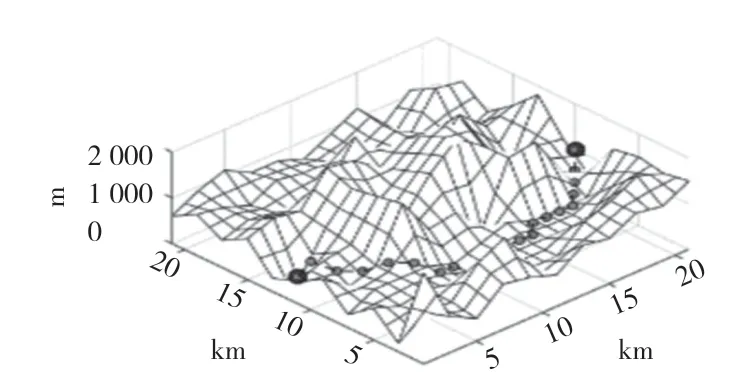
图5 本文改进算法Fig.5 Improved algorithm

图6 最优路径长度迭代次数变化曲线Fig.6 Variation curve of iterations number of optimal path length

由图3—图5 和表2 可知，本文的改进算法最优路径长度比蚁群算法减少了19%，比算法W 减少了14%；运行时间比蚁群算法减少了27%，比算法W 减少了52%。根据最适高度改进启发式函数后，改进算法寻找的路径更加跟随地形，不均匀的信息素分布加快了算法的收敛速度，在改进算法搜索窗口大小后，算法整体运行的时间也明显减小。

3.2 实验2

为检验算法的通用性，验证其在更加复杂的环境下的性能，采用30 km×30 km×2 km 的栅格地图，设置起飞点为（1，20，5），目标点为（31，19，5）。传统蚁群算法、算法W 和本文改进算法的实验结果分别如图7—图9 所示，3 种算法的路径长度与迭代次数对比如图10 所示。实验结果见表3。

表3 仿真实验结果Tab.3 Simulation experiment results

图7 蚁群算法Fig.7 Ant colony algorithm

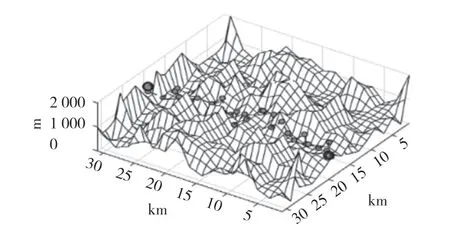
图8 算法WFig.8 Algorithm W

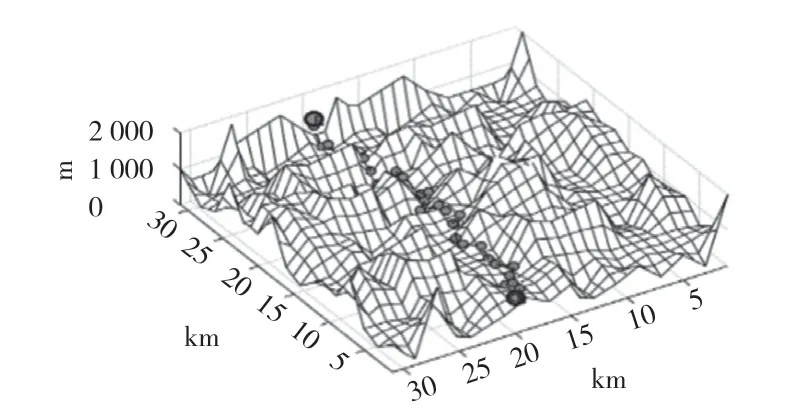
图9 本文改进算法Fig.9 Improved algorithm

图10 最优路径长度迭代次数变化曲线Fig.10 Variation curve of iteration number of optimal path length

结合图7—图9 和表3 可知，本文的改进算法得到的最优路径长度比蚁群算法减少了13%，比算法W 减少了9%；运行时间比蚁群算法减少了31%，比算法W 减少了60%。在更加复杂的环境中，本文改进算法依然可以找到最优路径，且所需时间大幅度减少。通过2 个实验结果可知，改进后的算法在不同环境下都能搜索到最优路径，且所需时间大大减少，证明了改进算法的优越性和可行性。

4 总结

本文为解决蚁群算法在求解无人机路径规划问题中遇到的运行时间长、局部最优等问题，采用不均匀的初始化信息素，在蚁群搜索过程中改变搜索窗口大小,根据无人机工作的最优工作高度改进启发式函数，对达到目的地最短的蚂蚁进行信息素更新等方法对蚁群算法进行改进。通过2组对比实验表明，改进后的蚁群算法比传统蚁群算法和算法W 最优路径长度更短，运行时间更短。