如何利用角平分线巧作辅助线
2023-10-28胡莲
语数外学习·初中版 2023年8期
胡莲

在一些几何问题中,常常出现有关角平分线的条件,能否恰地当利用角平分线巧作辅助线,往往成为解题的关键.下面举例说明如何利用角平分线作辅助线,来解答有关线段或者角的数量关系问题.
一、作垂线
当题目的已知条件中出现角平分线的时候,我们立刻想到它的性质定理:1.把已知角平分为两个相等的小角;2.角平分线上的点到角的两边的距离相等.因此,经过角平分线上任意一点作角的两边的垂线后,可以根据角平分线性质找到全等三角形,然后得到相等的边长和角度.
例1
证明
二、截取相等线段
当证明题中有角平分线时,常在角的两边截取相等的线段,构造全等三角形或等腰三角形,得到一些相等的线段和角度.运用这种作辅助线的方式解题,有截长和补短两个方向,即延长短的线段或在长的线段上截取一部分使之等于短的线段.无论延长还是截取都要证明线段的相等,进而达到所证目标.
例2
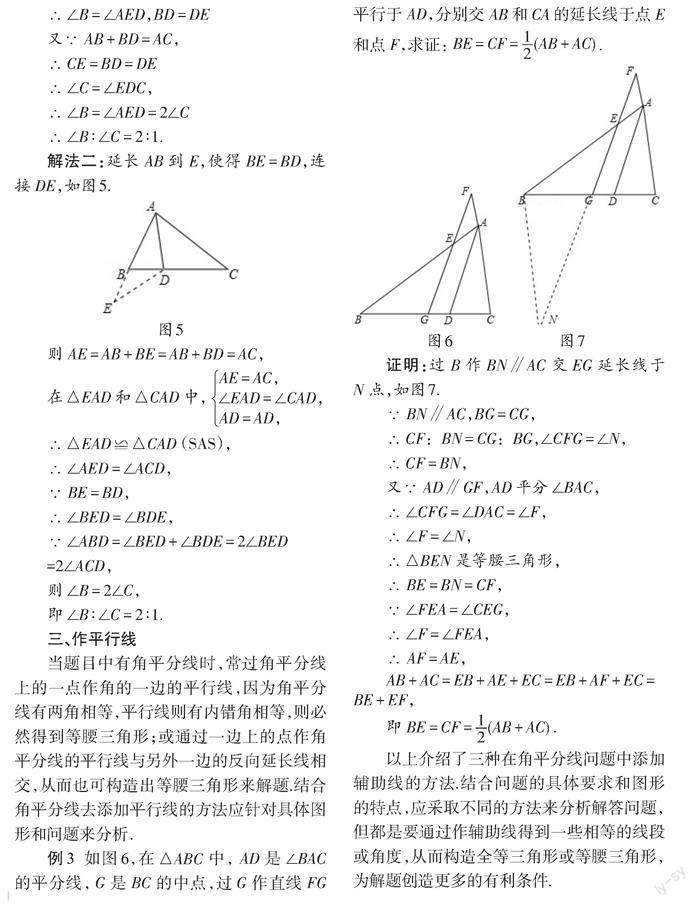
解法一
解法二
三、作平行线
当题目中有角平分线时,常过角平分线上的一点作角的一边的平行线,因为角平分线有两角相等,平行线则有内错角相等,则必然得到等腰三角形;或通过一边上的点作角平分线的平行线与另外一边的反向延长线相交,从而也可构造出等腰三角形来解题.结合角平分线去添加平行线的方法应针对具体图形和问题来分析.
例3
证明
以上介绍了三种在角平分线问题中添加辅助线的方法.结合问题的具体要求和图形的特点,应采取不同的方法来分析解答问题,但都是要通过作辅助线得到一些相等的线段或角度,從而构造全等三角形或等腰三角形,为解题创造更多的有利条件.
