基于输入变量筛选与卷积神经网络的黄河流域高精度灌溉用水空间栅格研究

张 敏

（太原理工大学建筑设计研究院有限公司，太原 030000）

0 引 言

水是维系生态系统和人类生活、生产活动的基本要素，随着社会经济的发展以及人口的增长，用水需求呈现出不断增加的趋势[1]，而气候变化的影响使得水资源供需矛盾更加突出[2]，因此合理优化配置以实现更高效地利用水资源成为缓解水资源短缺问题的关键[3]。水资源优化配置的关键在于明晰来水条件、用水状况以及水利工程能力，随着分布式水文模型的发展与研究，来水条件在不同时空尺度上均得到了有效的模拟和预测[4-6]；亦有众多学者提出了不同情景下的水资源多目标优化配置方案与算法[7,8]。然而，用水状况的研究仍然停留在以行政区为单元的统计调查尺度[9]。来水条件的空间尺度往往是具有流域特征的水资源分区，导致用水状况与来水条件之间存在着的空间尺度不匹配问题，这给水资源的配置带来了挑战，增加了供水的不确定性和缺水风险[10]。

农业灌溉是我国的用水大户，根据《2021 年中国水资源公报》，我国用水总量为5 920.2 亿m3，其中农业用水量3 644.3 亿m3，占总用水量的61.5%，因此研究农业灌溉用水的空间栅格化以保障精准灌溉对于我国农业的稳定稳产尤为重要。目前已有较多学者针对农业灌溉用水的用水效率[11,12]、用水定额[13]、影响要素[14]、用水预测[15]等方面开展研究，缺少对灌溉用水在空间分布上的研究。黄河流域在我国经济高质量发展和农业生产安全方面具有十分重要的地位，改革开放以来经济社会高速发展，水资源消耗不断增加，在保障黄河流域绿色发展的前提下维稳农业生产尤为关键[16]。

基于此，本文以黄河流域为研究对象，基于地理变量相互关系的思想，筛选与灌溉用水相关性强的地理变量（输入变量），利用卷积神经网络构建地理变量与灌溉用水（输出变量）的相互关系，通过输入变量的空间分布以及输入变量与输出变量的关系来实现灌溉用水的空间栅格化。以此为基础，分析黄河流域灌溉用水栅格的时空分布特性，以期为黄河流域灌溉用水的合理调配提供科学支撑，为黄河流域实现高质量发展提供决策参考。

1 研究区域与数据

1.1 研究区域

黄河发源于青藏高原巴颜喀拉山北麓，从西到东依次流经青海、四川、甘肃、宁夏、内蒙古等9 个省（自治区），全长5 464 km，流域总面积为79.5 万km2，在我国经济社会发展和农业生产安全方面具有十分重要的地位。黄河流域范围及流域内地级市边界如图1所示。

图1 黄河流域及流域内城市边界图Fig.1 Urban boundary map of the Yellow River Basin and its interio

1.2 数据来源与数据预处理

研究选取2000-2013 年黄河流域内77 个地级市（自治州）的灌溉用水量数据作为输出变量数据，数据来自于由Zhou等[17]构建的中国用水量数据集NLWUD（National Long-term Water Use Dataset of China）。数据主要来源于第一次和第二次全国水资源调查评价资料、省级行政区的水资源公报，具有较好的时间连续性和可靠性。

收集的地理变量包含土壤含水量数据、社会经济数据（GDP、人口）、气象站点数据、遥感影像数据（归一化植被指数）、土地利用/覆盖数据、DEM 数据等。其中土壤含水量数据来源于He 等[18]发布的VIC 水文模型模拟数据，社会经济数据来源于中国科学院资源环境科学与数据中心（www.resdc.cn），气象站点数据来源于中国气象数据网（data.cma.cn）。

由于收集的地理变量在时空尺度上存在多样性，为了实现时空尺度的统一（年尺度，空间尺度1 km），需要对数据进行预处理。预处理的方法包含两类：时间尺度的升/降尺度，空间尺度的升/降尺度。土壤含水量数据原始空间尺度为0.25°×0.25°，采用一种基于地理变量的机器学习算法[19]降尺度到1 km×1 km；社会经济数据则在时间上进行线性内插，土地利用/覆盖数据与DEM 数据采用最邻近法进行重采样升尺度，气象站点数据则采用反距离加权法进行空间插值。数据详情与预处理方法如表1所示。

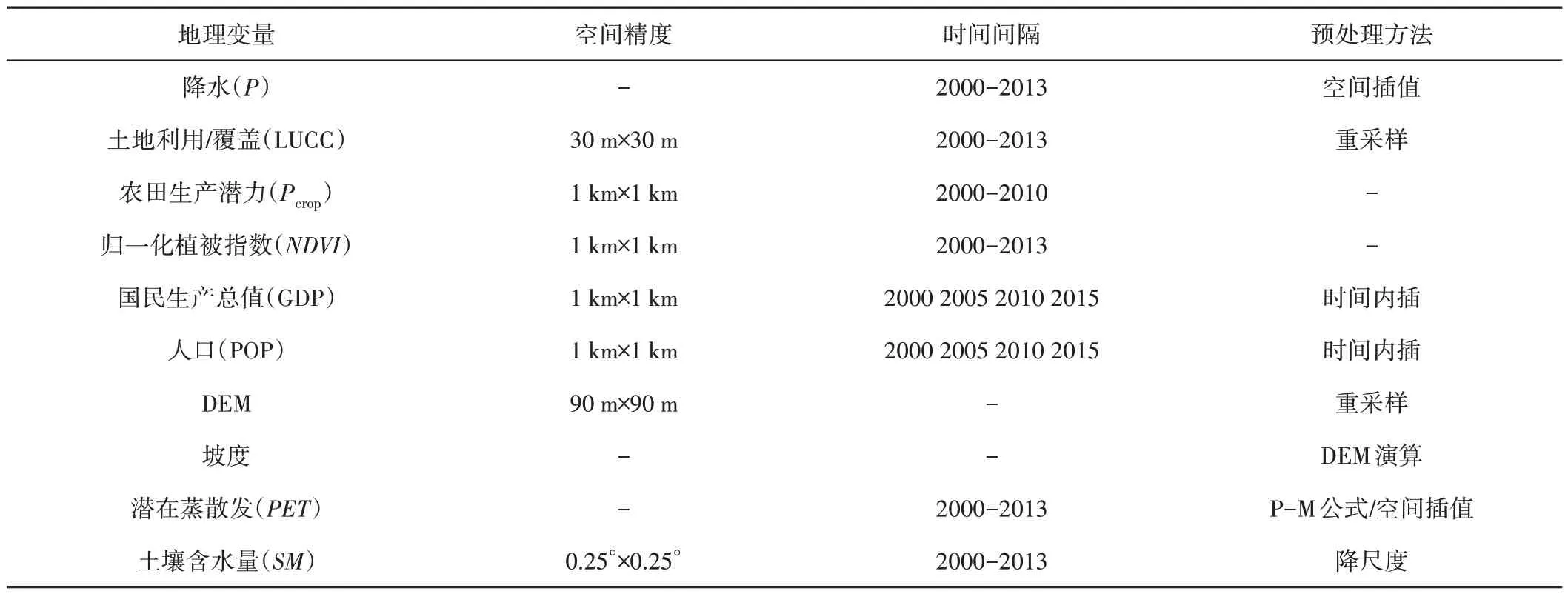
表1 地理变量数据详情与预处理方法Tab.1 Details of geographic variable data and preprocessing methods

2 研究方法

2.1 地理变量相互关系法与地理变量筛选

地理变量相互关系法，简单来说就是建立目标变量和输入变量的相互关系。通过输入变量的空间分布，利用输入变量与目标变量的关系来展现目标变量的空间分布。这一方法在社会数据空间化的研究中应用广泛，随着GIS 与遥感数据发展，研究的趋势也从单一数据源逐渐向多元复合数据源前进。

对收集到的地理变量，采用Spearman 相关分析筛选地理变量，Spearman相关系数的计算如下：

式中：n 为2000-2013 年77 个地级市的总样本数；di为通过排序得到的第i个奇偶样本之间的位置偏差。

根据各地理变量与输出变量（灌溉用水）的相关系数，最终筛选地理变量作为之后模拟模型的输入变量。

2.2 卷积神经网络的工作原理及流程

通过地理变量筛选确定输入变量后，采用卷积神经网络构建输入变量与灌溉用水的关系并实现灌溉用水的空间栅格化模拟。

卷积神经网络（Convolutional neural network，CNN） 是一种具有交替卷积层和子采样层的前馈神经网络[20]。卷积神经网络的典型架构由输入层、卷积层、池化层、全连接层和输出层组成。卷积层学习输入变量的卷积，并为特征提取提供最佳性能。池化层降低了输入变量中特征的维数，而不改变这些输入变量的信息从而提高CNN 的计算效率。完全连接层可以重新组织提取的特征，以减少输入变量中的信息损失。CNN 在面对不同维度的输入变量时具有自适应能力，由于本研究中采用的输入数据具有二维形式，且CNN-2D 架构已被证明能够有效映射时间连续的二维形式输入变量[21]，因此，本文采用CNN-2D 架构进行黄河流域灌溉用水的空间栅格化。

研究方法流程图如图2所示。

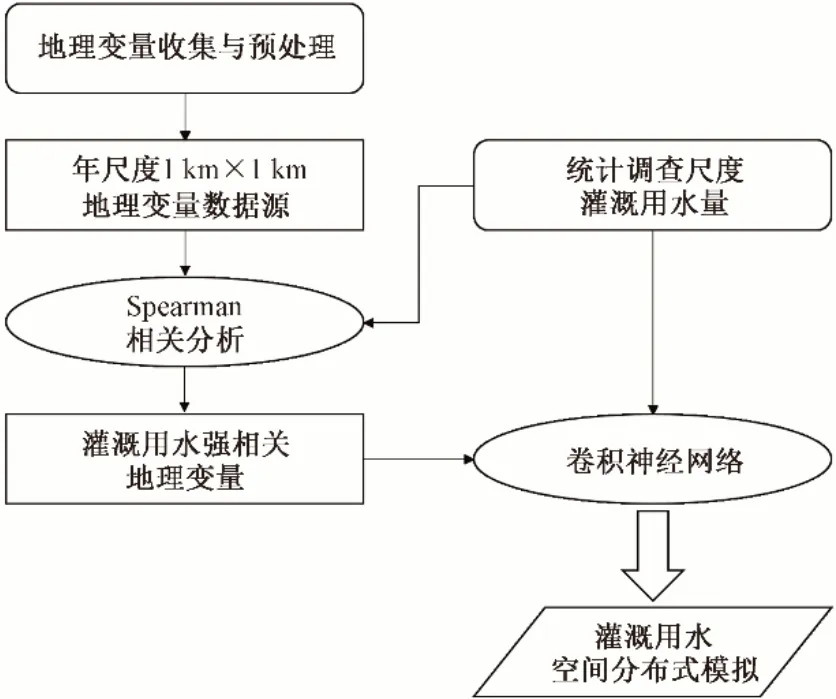
图2 研究流程图Fig.2 Flowchart of research

3 结果分析

3.1 地理变量筛选结果

利用Spearman 相关分析方法，最终从收集的10 个地理变量（降水、土地利用/覆盖、农田生产潜力、归一化植被指数、GDP、人口、DEM、坡度、潜在蒸散发、土壤含水量）中筛选出6个输入变量，分别为：潜在蒸散发（PET），降水（P），归一化植被指数（NDVI），土壤含水量（SM），净初级生产力（NPP）和农田生产潜力（Pcrop）。

这6 个输入变量与输出变量（灌溉用水IWU）之间的Spearman相关系数热力图如图3所示。

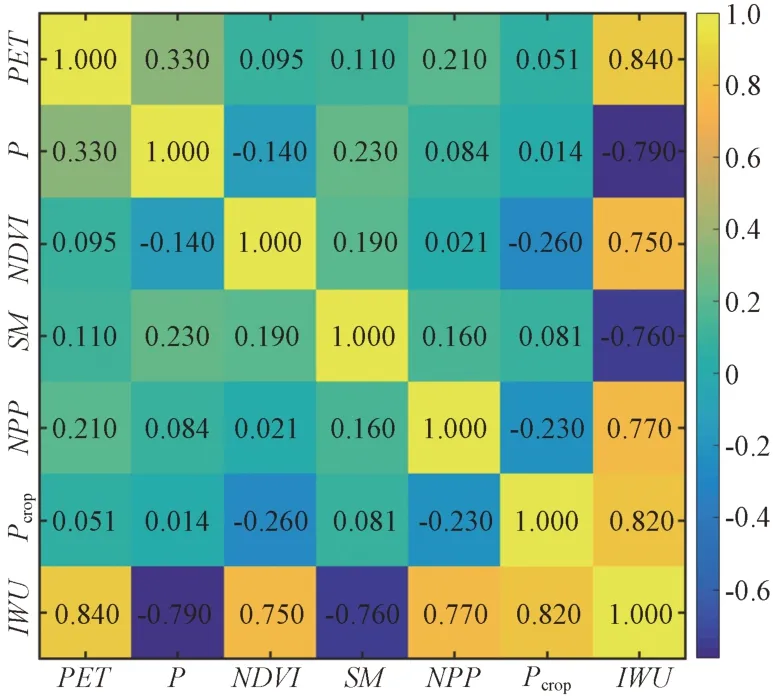
图3 输入变量与灌溉用水Spearman相关系数热力图Fig.3 Thermal diagram of spearman correlation coefficient between input variables and irrigation water

由Spearman相关系数热力图可得6个输入变量与灌溉用水的相关系数，其中潜在蒸散发[22]和农田生产潜力与灌溉用水的相关系数较高，达到0.82 以上；净初级生产力和归一化植被指数次之，在0.75 以上；降雨和土壤含水量与灌溉用水的关系为负相关，且相关系数在0.76以上。

出现此类结果的原因在于，灌溉用水主要用于作物在降雨量及土壤含水量之外正常生长发育所需的额外水量，故而灌溉用水与降雨和土壤含水量呈负相关；同时，作物生产力越高、植被覆盖率越大，则构成植物体所需的水量之和也就越大，灌溉用水量就越大，因而，灌溉用水与净初级生产力和归一化植被指数呈正相关；而灌溉用水在正常生长发育过程中，主要用于作物蒸腾、棵间蒸发以及构成植株体的水量之和，因次，潜在蒸散发和农田生产潜力与灌溉用水的相关系数最高，并呈正相关。

3.2 灌溉用水空间栅格模拟精度评价

采用均方根误差（Root Mean Squared Error，RMSE）、纳什效率系数（Nash-Sutcliffe Efficiency，NSE） 与相对误差（Relative Error，RE）3 个指标对模拟的灌溉用水空间栅格进行精度评价，将黄河流域灌溉用水的空间栅格在地级市边界内统计，与各地级市统计调查的2000-2013年灌溉用水量进行对比，各评价指标如图4～图6所示。

图4 黄河流域灌溉用水空间栅格RMSE空间分布图Fig.4 Spatial grid RMSE spatial distribution map of irrigation water use in the Yellow River Basin

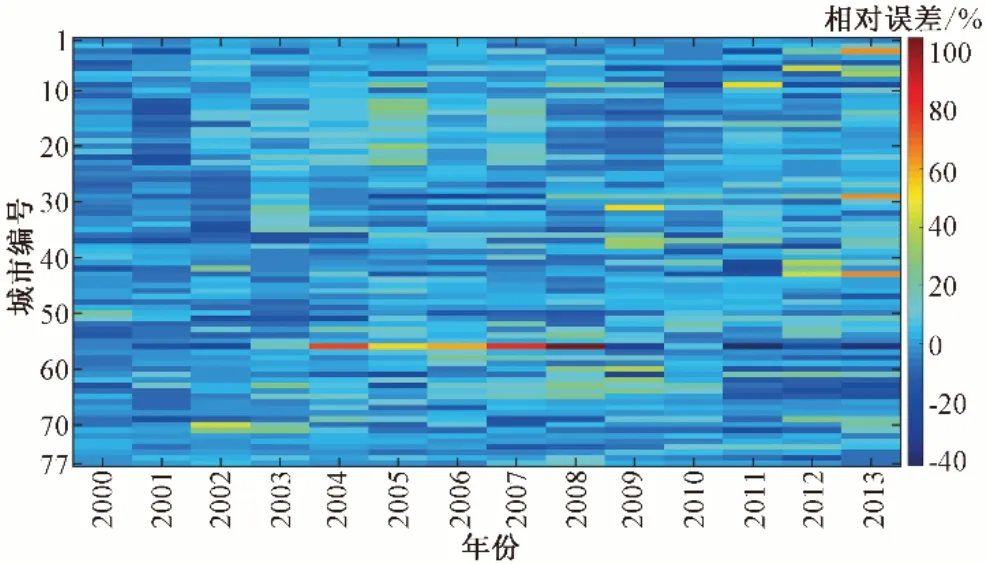
图5 黄河流域灌溉用水空间栅格相对误差Fig.5 Relative error of spatial grid for irrigation water use in the Yellow River Basin

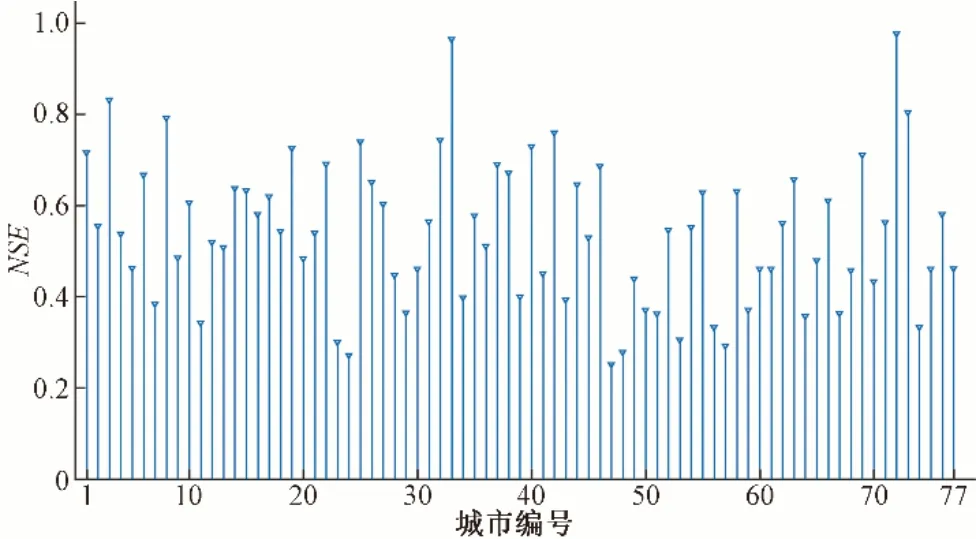
图6 黄河流域灌溉用水空间栅格NSEFig.6 Irrigation water spatial grid NSE in the Yellow River Basin

由图4可知，在河套地区以及黄河下游地区，模拟的灌溉用水空间栅格的均方根误差较大，而在其他地区均有着较高的模拟精度。由此也可看出，河套地区及黄河下游地区灌溉用水量远高平均值，造成该结果的主要原因为：该区域地势平坦，作物种植面积大，农田生产潜力、净初级生产力和归一化植被指数同其他地区相比较高，而且，由于气候干燥昼夜温差大，潜在蒸散发能力强，同时降雨不足[23]，土壤含水量低造成该区域灌溉用水远高平均值。

各城市在不同年份间的模拟精度也有所不同（图5），如山西晋城市，相对误差在2000-2013 年间变化幅度较大，在2008 年相对误差为105%，这是由于晋城市灌溉用水在2000-2013年间变化幅度较大，2000-2008年间维持下降趋势，而在2008-2013 年间迅速增长，2008 年晋城市灌溉用水量为0.035亿m³，而在2013 年灌溉用水量增长至0.144 亿m³，增长幅度巨大导致模型模拟精度在2008年尤为差。

模拟的灌溉用水空间栅格的NSE 值整体维持在可接受范围内，大部分城市NSE值均大于0.4，部分城市NSE值大于0.8（图6）。由此，模型模拟的灌溉用水空间栅格精度较高，能够较好地展现灌溉用水的空间分布状况。

3.3 灌溉用水栅格时空特性分析

模拟的2000-2013 年黄河流域灌溉用水空间栅格如图7 所示。由图7可知，灌溉用水的高值主要集中在甘肃地区、宁夏平原、河套平原、渭河、汾河两岸以及花园口以下地区。出现此类现象的主要原因是：原始的气候因素如甘肃及宁夏地区气候干燥，昼夜温差大，当地作物潜在蒸散发能力强，因而需水量高；灌溉面积因素如河套平原区，地势平坦，作物种植面积大，导致的需水量高；灌溉条件成熟如渭河、汾河两岸土壤肥沃，灌溉条件优越，故而所需水量高；作物种植模式如花园口以下地区作物种类多样，故而需水量高。其综合因素均体现为潜在蒸散发强，降水少，归一化植被指数高，土壤含水量低，净初级生产力高和农田生产潜力高等，该结果同地理变量筛选结果保持一致。

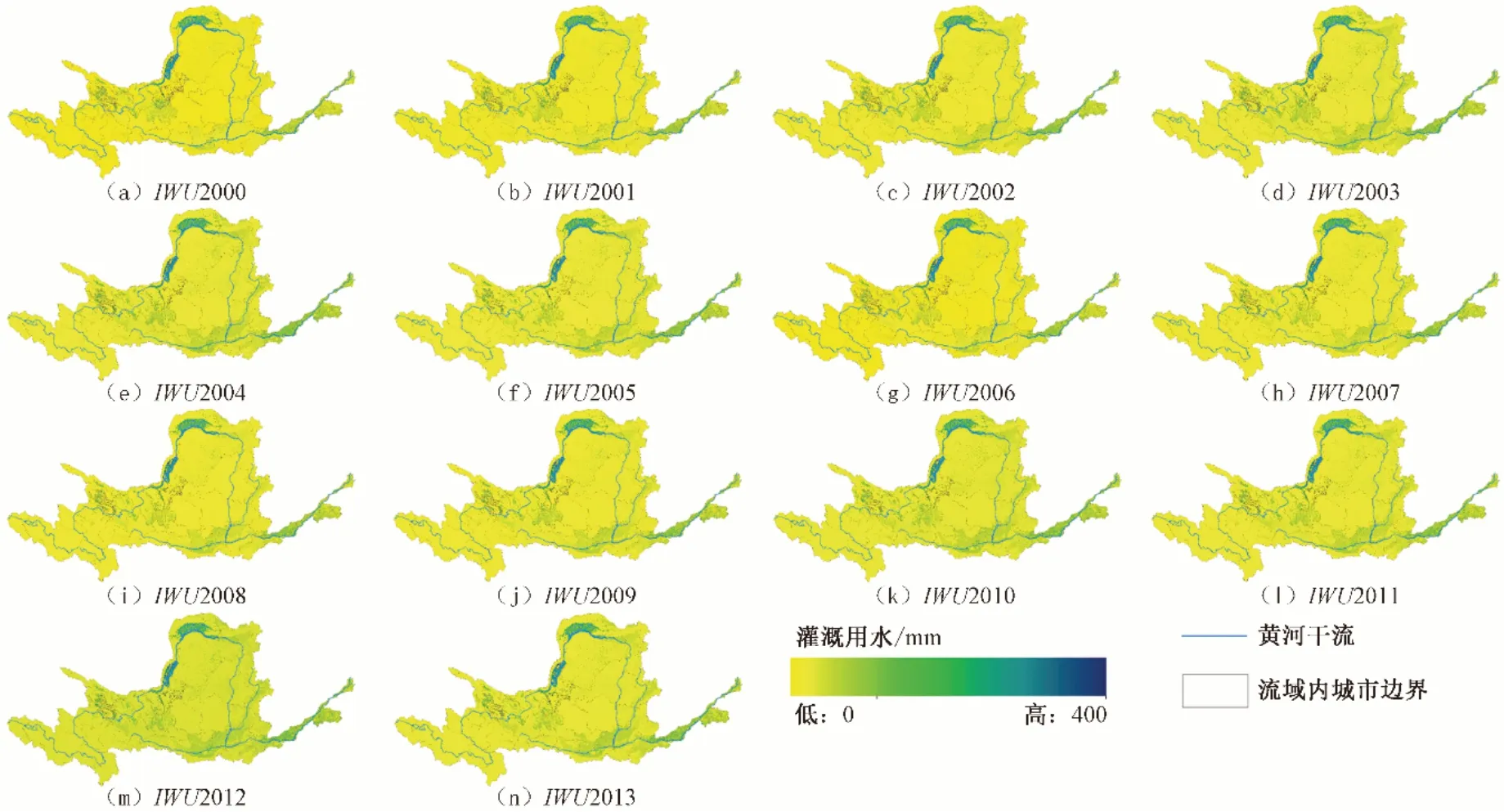
图7 黄河流域2000-2013年灌溉用水空间栅格Fig.7 Spatial grid of irrigation water use in the Yellow River Basin from 2000 to 2013

灌溉用水量在不同年份之间存在着分布差异，但空间用水整体稳定，能够为黄河流域灌溉用水的合理调配提供科学支撑。

为了探究黄河流域灌溉用水空间栅格的空间自相关性，采用全局莫兰指数进行空间自相关性的检验。黄河流域灌溉用水空间栅格的全局莫兰指数如表2所示。黄河流域灌溉用水量的全局莫兰指数均保持在0以上，表明黄河流域的灌溉用水量呈现正向的空间集聚，即整个流域在地理空间具有较好的空间自相关性，其空间属性间聚合程度较好，并且灌溉用水的空间集聚在2000-2013年间有所下降（全局莫兰指数减小），即空间差异性随时间拉大。该结果说明了将黄河流域作为一个分析系统是完全合理的。

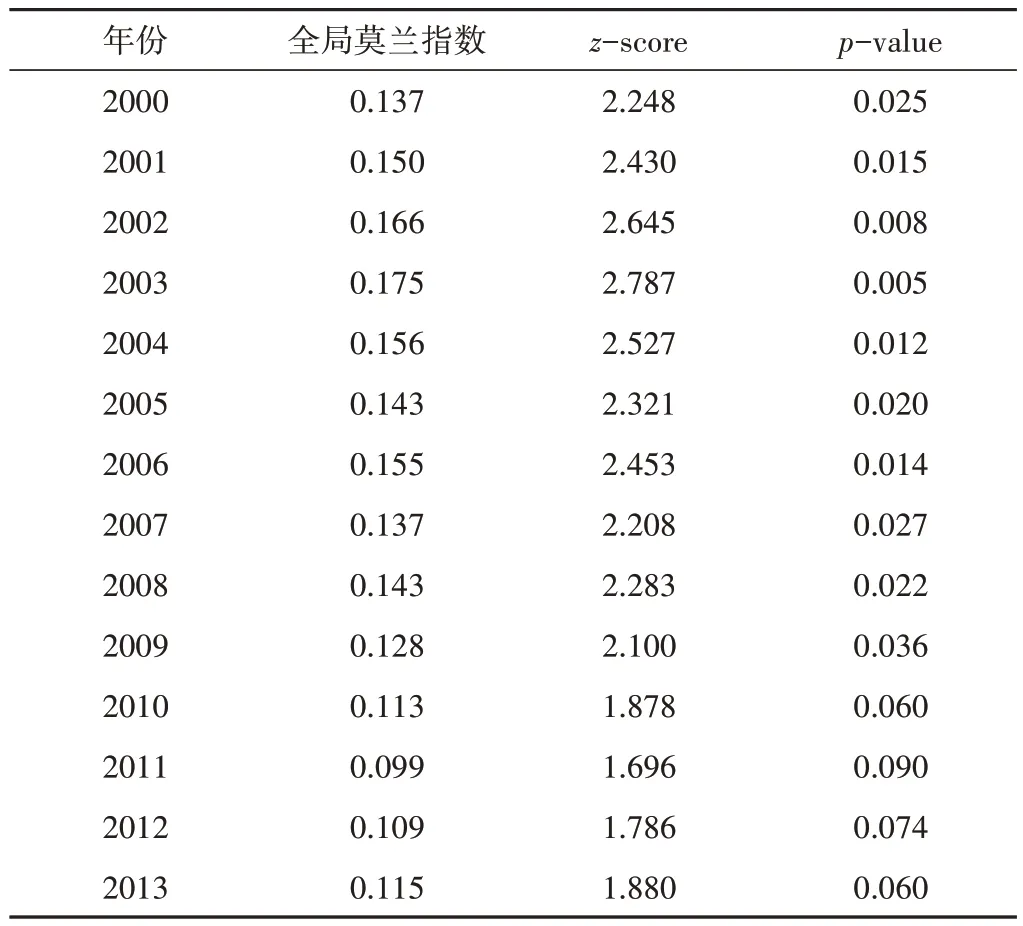
表2 黄河流域灌溉用水空间栅格全局莫兰指数Tab.2 Global Moran's index of spatial grid of irrigation water use in the Yellow River basin

在时间演变规律上，黄河流域灌溉用水年均变化率如图8所示。由图8 可知在黄河流域大部分地区，灌溉用水较为稳定，年均变化率不高，可以为黄河流域灌溉用水提供较为精确的灌水预测，为黄河流域实现高质量发展提供决策参考。仅在青海西宁市、甘肃天水市和山西晋城市，年均增长率较高，分别为6.04%、5.12%、12.14%，其中山西晋城市灌溉用水量年均增长率最高；在甘肃甘南藏族自治州，灌溉用水量年均减少率最高，为-5.49%。

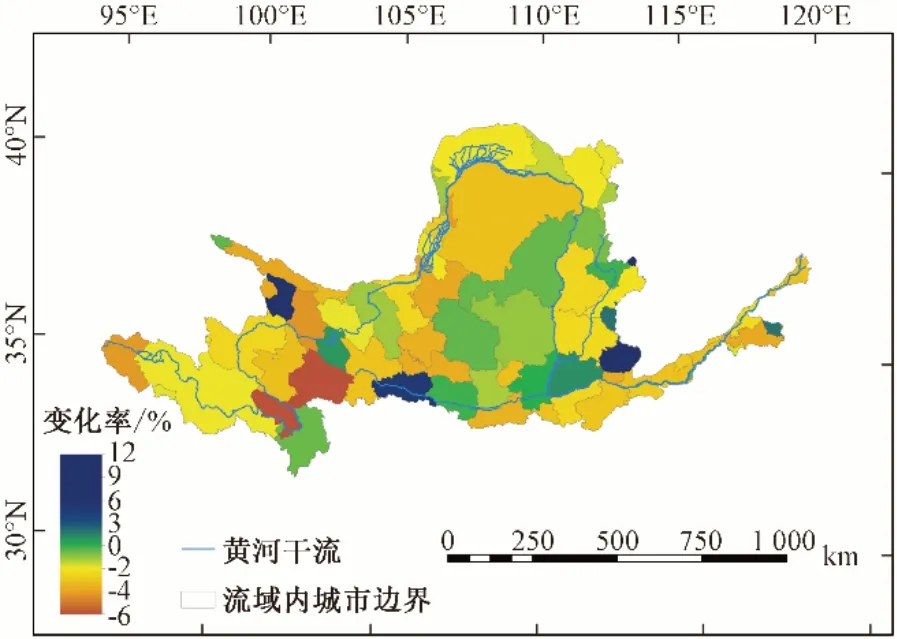
图8 黄河流域灌溉用水年均变化率Fig.8 Annual average change rate of irrigation water use in the Yellow River Basin

4 结 语

本研究基于地理变量相互关系法，通过筛选与灌溉用水高相关的地理变量，利用卷积神经网络，实现了黄河流域内灌溉用水的空间栅格化。

利用Spearman 相关分析筛选的与灌溉用水强相关的地理变量分别为：潜在蒸散发、降水、归一化植被指数、土壤含水量、净第一生产力和农田生产潜力。利用卷积神经网络模拟的2000-2013 年黄河流域灌溉用水空间栅格在精度上较高，误差在可接受范围内。黄河流域的灌溉用水在空间上呈现正向的集聚性，且集聚性有随时间逐渐降低趋势。在时间演变上，黄河流域内不同地区的灌溉用水有着不同的年际变化趋势，在山西晋城有着最高的年均增长率，而在甘肃甘南藏族自治州则有着最高的年均减少率。

由于黄河流域面积广阔，上中下游气候条件、土壤类型和来水条件等差异较大，明晰灌溉用水在黄河流域内的空间分布，可为黄河流域灌溉用水的合理调配提供科学支撑，并且能够为保障黄河流域高质量发展与农业稳产提供决策参考。