基于探地雷达功率谱属性参数的土壤含水状态预测

2023-10-28谢国青聂俊丽陈紫秋熊悦意冯艳玲陈德文

节水灌溉 2023年10期

谢国青，聂俊丽，陈紫秋，熊悦意，冯艳玲，陈德文

（1.贵州大学国土资源部喀斯特环境与地质灾害重点实验室，贵阳 550025；2.贵州大学资源与环境工程学院，贵阳 550025）

0 引言

土壤含水率(SWC)是表征土壤水分状况、反映土体组成的重要指标，准确测定土壤含水量在土木工程、农业生产和生态修复方面发挥着关键作用[1,2]。常规的土壤含水率测量方法需要对土层进行钻孔取样，该方法测量结果虽然直观准确，但容易破坏土层结构完整性且采样费时费力。因此，研究一种无损快速准确探测土壤含水构造的方法，对农业生产、生态环境保护等具有重要意义。探地雷达(GPR)是一种通过高频电磁波推测地质体空间结构和物性参数的地球物理方法，具有无损、快速、探测精度高等优点，近年来，已被广泛应用于中尺度范围内土壤含水率的探测研究中[3-5]。现有的探地雷达探测土壤含水率的方法多利用信号时域属性，通过时域信号估算土壤介电常数并建立相应的关系模型来估算土壤含水率，具有原理简单易于实现的优点，但时域方法反演含水率精度受到反演得到的介电常数及相关关系模型的影响，容易产生误差的二次传递[6]。近年来，越来越多的学者开始研究基于雷达信号频域功率谱估计土壤含水率的方法。杨峰首次将功率谱方法引入路基含水率计算中，提出利用路基材质与水介质对应的功率谱面域能量比值经验公式进行含水率求取与路基富水病害判别。通过雷达检测频谱分析结果与现场取样试验室分析结果对比，归纳总结出对应于模型的雷达波峰谱面域与不同介质元素的峰谱面域构成比例关系[7]。聂俊丽基于ARMA 功率谱估计方法，成功的反演了风积沙地区的砂壤含水率[8]。张浩浩采用ARMA 功率谱分析方法，通过物理实验研究了不同路基病害的雷达信号频谱响应特征，并基于雷达信号响应特征成功地对模型路基富水病害进行了识别[9]。郑龙金针对地下富水异常体探测提出利用功率谱能量统计值与滚动功率谱结合的方法判别富水区域分布情况，并利用谱面域经验公式对富水体含水率进行计算[10]。崔凡等人提出了对功率谱频带进行划分，选择了一个频率分界点，计算低频叠加与整个频谱能量的比值，并建立该值与实测土壤含水率的关系模型，随后使用关系模型成功地反演了0～10 m 砂壤的含水率[11]。前人在利用功率谱方法反演土壤含水率的研究中，仅考虑功率谱单一属性与土壤含水率的关系，并未对功率谱属性进行全面研究，主要方法为通过建立功率谱能量或频域属性与土壤含水率之间的关系模型进行含水率探测。为此，本文在前人对功率谱属性研究基础上，采用属性分析方法提取功率谱多种属性参数，并基于物理模型探地雷达数据，利用探地雷达功率谱属性参数和BP 神经网络相结合的方法对土壤含水率进行预测，以期达到快速准确计算土壤含水率的目的。

1 材料与方法

1.1 物理实验

建立了长宽高分别为1.8、1.0、0.8 m 的不同含水率物理模型，采用5 mm 筛网对土壤进行细筛，使用主频天线为400 MHz 探地雷达对模型4 个采样点进行点测，采样时窗为30 ns，采样点数为1 024。测完后从模型由上至下每间隔10 cm 进行环刀取样，每层在雷达点测处取样，连续取得8个不同深度的土壤样本。一次探测结束后使用搅拌机对土样进行搅拌，每次喷洒相同体积水，搅拌半小时后装入模型静置12 h 后进行探测，共采集了8组不同含水率土壤模型，最后将采集到的土壤样本带回实验室。按照规范《LY/T 1213-1999 森林土壤含水量的测定》的要求，采用烘干法测量样本土壤含水率以及土壤容重等参数，其模型平均含水率见表1。

表1 实测模型含水率Tab.1 The measured water content of the model

1.2 野外实验

采样区域位于贵阳市贵州大学(106°39'19″E，26°26'55″N)，采样点一位于贵州大学物探试验场内，地表植被裸露，地表潮湿土壤含水率较高；采样点二位于贵州大学野外空地，地表覆盖植被，且表层含有薄薄一层腐殖质，为提高探测效果，对探测区域进行了整理，铲除地表植被与累积的腐殖质。首先使用400 MHz天线进行点测，采样时窗为35 ns，采样点数为1 024；然后在测点中间自上而下每隔10 cm 取一个样，取样深度为0.8 m。

1.3 功率谱方法原理及属性提取

假定离散信号x(n)是由一个输入序列u(n)通过一个线性时不变系统H(z)输出所得，通过已知x(n)及其自相关函数rx(m)来估计线性系统H(z)的参数，最后利用H(z)的参数求解信号x(n)功率谱的方法称为现代功率谱分析方法。

离散随机信号x(n)与白噪声方差为σ2的随机噪声u(n)总有如下关系：

其中若b1,b2,…,bq全为零，则式(1)称为自回归(autoregressive,AR)模型，该模型表示当前输出信号是由前p 个延迟信号和现在的输入加权而成；若a1,a2,…,ap全为零，则式(1)称为滑动平均(moving-average,MA)模型；若b1,b2,…,bq和a1,a2,…,ap不全为零时则称式(1)为自回归滑动平均(Auto-Regressive Moving Average Model)模型。其中由于AR 模型参数计算简单，具有较高谱分辨能力，任意的MA 和ARMA 模型都可以由AR模型有限阶推出，所以在功率谱估计中AR 模型应用较多[12]，因此本文选择使用AR 模型作为探地雷达信号功率谱估计的方法。

当b1,b2,…,bq全为零时，式(1)可看作信号x(n)是由k 个随机噪声u(n)和线性随机系统H(z)的关系式：

输入信号u(n)与通过线性随机系统H(z)后输出的信号x(n)有如下关系：

由公式(2)～(5)，得x(n)的p阶AR模型功率谱密度为：

从式(6)可看出当确定AR模型的参数a1,a2,…,ap，白噪声方差σ2和AR 模型阶数p 时，便可得到x(n)的功率谱，其中AR 模型的参数a1,a2,…,ap和白噪声方差σ2可利用Yule-Walker 方程解出：

为实现利用功率谱属性反演土壤含水率，本文在前人的研究基础上从功率谱在频域、能量、聚合程度和能量分布等4个特征属性角度对雷达信号功率谱进行分析，提取雷达功率谱属性共11种[13-16]，表2给出关于功率谱属性的提取方法。

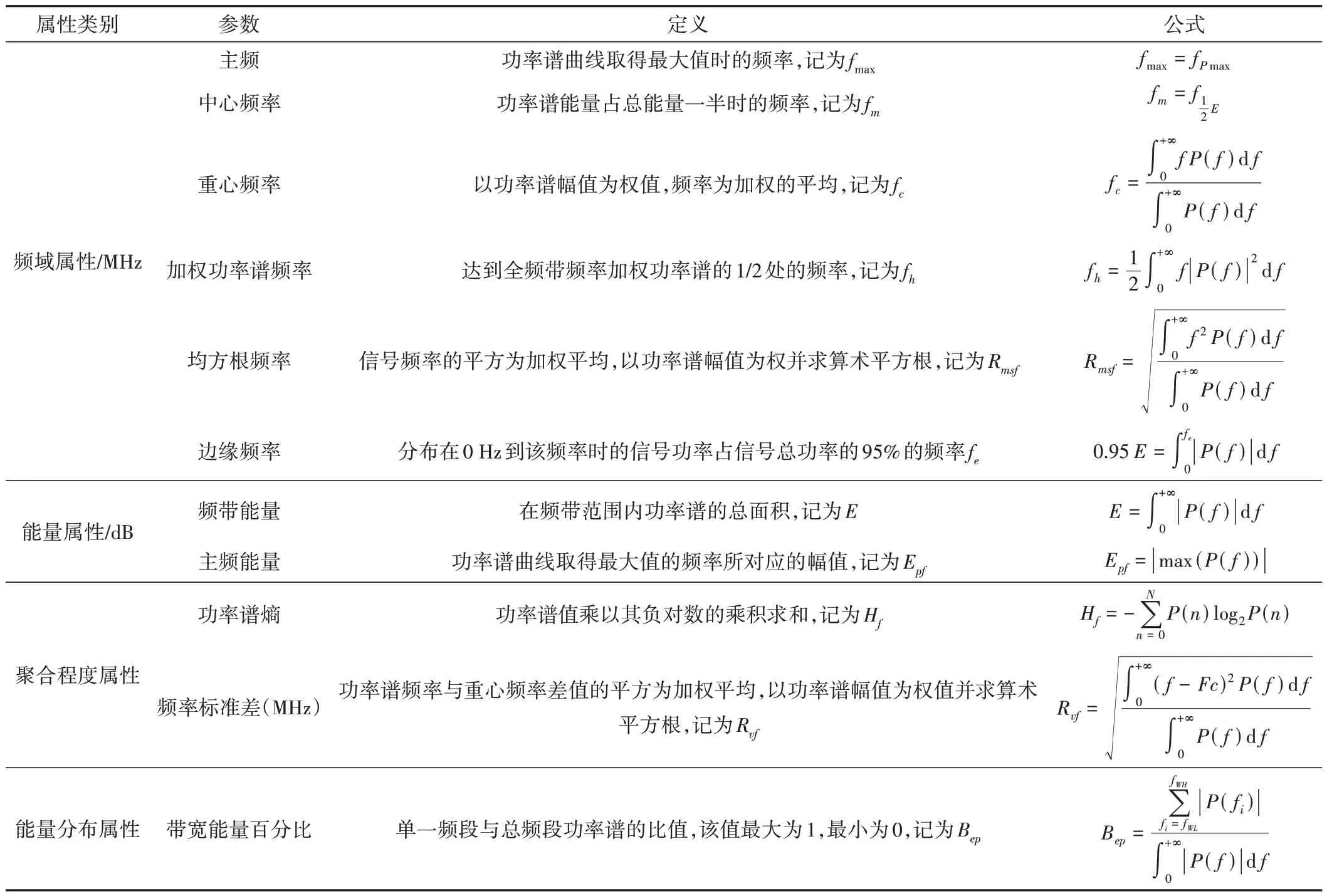
表2 功率谱参数属性表Tab.2 Power spectral parameter attribute table

1.4 神经网络预测模型构建方法

BP 神经网络具有强大的学习、记忆、容错、非线性和自适应能力，可通过反复学习大量数据实现输入到输出的映射，数学理论证明三层神经网络可逼近任何非线性连续函数，使其特别适合于求解内部机制复杂的问题，即具有较强的非线性映射能力[17-19]。因此本文选择BP 神经网络方法对土壤含水状态进行预测。BP 神经网络主要分为输入层、隐含层和输出层，其中隐含层中每层的节点又称为神经元，通过输入层样本在神经网络中正向传播得到输出类别与预期输出进行对比，将分类误差不断反向传播改变隐含层神经元之间的连接权值，使得输入样本通过神经网络的输出与事实输出一致。其算法流程如图1所示，主要分为输入数据预处理、网络设计、正向传播和误差反向调整4个部分。

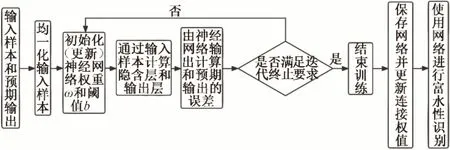
图1 BP神经网络预测算法流程图Fig.1 Backpropagation neural network prediction algorithm flowchart

(1)确认输入样本数据及预期样本输出数据，并对输入样本数据做归一化等预处理。

(2)设计神经网络层数、神经元个数并初始化各层各神经元的权重和阈值。

(3)根据输入层样本数据确认隐藏层输入数据，并根据隐含层激活函数计算隐藏层输出。

(4)由隐含层输出数据计算输出层输入数据，根据输出层激活函数计算神经网络实际输出数据。

(5)依据实际输出数据与期望输出数据计算两者之间的总误差。

(6)将总误差通过隐含层与输出层之间的权重值传递并更新连接权重。

(7)将隐含层之间的误差传递至输入层与隐含层并更新连接权重。

通过设置迭代次数与精度，利用输入样本和预期输出不断更新输出层、隐含层和输出层之间的神经元连接权值直到迭代次数和误差满足精度要求后停止神经网络学习，并保存更新后的权值，这便是一个完整的BP 网络预测算法流程。将测试数据输入神经网络即可完成对输入数据的输出预测。

1.5 数据处理

物理实验和野外实验探地雷达数据预处理、雷达信号功率谱估计、功率谱属性参数提取优化、BP 神经网络模型建立及滚动时间窗剖面技术在MATLAB2020a 中通过编程实现，采用SPSS 22.0进行功率谱属性和土壤含水率的Pearson 相关性分析，使用Origin 2020进行作图。

2 结果与分析

2.1 物理实验结果

在数据采集结束后，使用MATLAB 编写的预处理程序进行零点校正、背景去噪以及滤波等处理。通过模型底部反射面确定实验模型的雷达信号时窗范围，并采用时窗选取压缩变换技术截取模型范围内的雷达信号，利用AR 功率谱法提取雷达雷达信号的功率谱(图2)，并根据表2 提取探地雷达功率谱参数，计算探地雷达功率谱参数与含水率之间的相关系数R1(表3)。

图2 物理实验400 MHz探地雷达功率谱图Fig.2 Power spectral diagram of 400 MHz ground penetrating radar for physical experiment

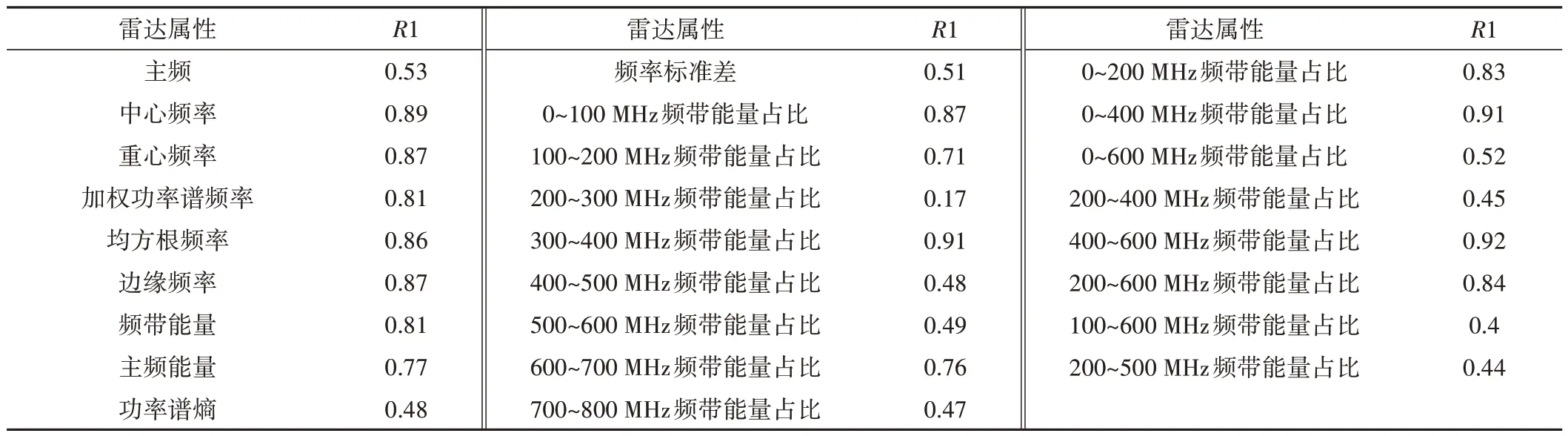
表3 物理实验(R1)功率谱属性参数与含水率相关系数Tab.3 Physical experiment (R1): correlation coefficients between power spectral attributes parameters and moisture content

如图2 所示，图中横坐标为频率(MHz)，纵坐标为含水率(cm3/cm3)，垂坐标为能量(dB)。从图2 中可以看出在天线为400 MHz 的功率谱中，其功率分布的频带主要在0～800 MHz，其功率能量主要分布在0～20×10-12dB 范围内；随着土壤含水率的增高，探地雷达信号的功率谱能量逐渐降低；功率谱的能量分布频带逐渐向低频偏移；功率谱能量分布逐渐聚集；功率谱曲线更加简单；并且功率谱随着土壤含水率的增加，低频的能量占比也逐渐升高。

从表3中可以看出物理实验中的探地雷达功率谱属性参数中聚合程度属性参数与土壤含水率相关性下降程度较快，频率属性参数和能量分布属性参数与土壤含水率相关性受探测条件影响较小。从表3中可看出，与土壤含水率相关关系大于0.3的属性参数个数为25个，但提取出来的探地雷达属性之间并不一定互相独立，为优化选择与含水率相关性大且属性之间相关性较小的功率谱属性参数，采用互相关法对功率谱属性参数进行优化选取。按照统计学中的定义，相关系数R介于0.75～1.00 两者呈强相关性，介于0.3～0.7 两者呈中等相关，考虑到计算精度、属性类别及空间冗余程度的影响，选择与含水率相关系数大于0.5 的功率谱属性进行互相关，其互相关关系如图3所示。

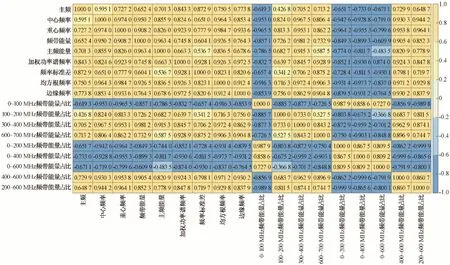
图3 400 MHz功率谱属性参数互相关热力图Fig.3 Thermographic map of cross-correlation of power spectral attribute parameters at 400 MHz

从图3中可看出，表征雷达功率谱频率的属性参数：中心频率、重心频率、加权功率谱频率和均方根频率的互相关系数均大于0.8，且呈显著正相关关系；表征雷达功率谱能量的属性参数：频带能量和主频能量的互相关系数为0.963，呈显著正相关关系；表征雷达功率谱能量各频带占比属性参数：0～100、0～200、0～400、0～600 MHz 频带能量占比相关系数均大于0.7，呈显著正相关关系，300～400 和200～600 MHz 频带能量占比相关系数大于0.7，呈显著正相关关系，600～700 和400～600 MHz 频带能量占比相关系数为0.897，呈0.01 水平的显著正相关关系。对上述呈显著正相关关系的属性参数结合与含水率的相关关系选取优化，选出主频、重心频率、边缘频率、频带能量、频率标准差、0～400 MHz 频带能量占比、400～600 MHz 频带能量占比等7 项功率谱属性参数作为探地雷达功率谱特征属性参数计算土壤含水率。

2.2 BP神经网络预测土壤含水率结果

2.2.1 基于功率谱属性与BP神经网络的土壤含水率定性识别

首先通过塑、液限实验测得贵阳市红黏土液限为53.3%,塑限为30.58%，因此选定含水率30%为土壤含水率富水界限。然后引入混淆矩阵及相关性能评价指标对神经网络识别土壤富水精度进行评价，混淆矩阵[20-22]是将分类模型中识别正确和错误的样本进行统计，放入矩阵中表现出来。

如表4 所示，TP 为正类识别为正类的个数、TN 为负类识别为负类的个数、FN 为正类识别为负类的个数、FP 为负类识别为正类的个数。除此之外，精确率、召回率、特异度、准确率、曲线下面积和F1 值也能从另一个方向衡量分类模型的性能，表5对各个指标进行了简单介绍。

表4 二值分类混淆矩阵Tab.4 Confusion matrix for binary classification

表5 神经网络性能评价指标介绍Tab.5 Introduction to performance evaluation metrics for neural networks

根据2.2 物理实验功率谱属性参数互相关分析结果，选择400 MHz天线中的功率谱属性参数：主频、重心频率、边缘频率、频带能量、频率标准差、0～400 MHz频带能量占比、400～600 MHz 频带能量占比等7 个功率谱属性参数作为神经网络的输入样本，输出层有2个节点用于判断土壤是否富水。

选取物理模型实验中土壤含水率小于30%的7 组模型中60 道雷达信号，大于30%含水率模型中120 道雷达信号，共计540道信号计算其功率谱特征参数，并将其作为含水率雷达功率谱参数样本库，随机选取功率谱参数样本的70%作为模型训练样本，30%作为模型测试样本进行土壤富水性识别。通过持续地学习过程中对神经网络参数的调整，发现网络的隐含层数、隐含层节点数、学习效率及训练次数分别为3 层、10 个节点、学习效率0.15 及训练30 000 次时，得出BP 神经网络识别富水体模型效果最佳，其混淆矩阵与评价指标见图4和表6。

表6 神经网络性能评价Tab.6 Performance evaluation of neural networks

从图4 和表6 可看出，神经网络模型对非富水土层的召回率为100%，对富水土层的特异度分别为83.3%，对于非富水土层的精确率分别为95.5%，总体样本预测准确率分别为96.3%，表明神经网络模型对土壤富水性的实测预测精度较高；就模型分类性能而言，F1 值为0.988，AUC 为0.99，证明模型分类可靠，预测能力极好，精度较高。总的来说BP 神经网络可以满足对于检测土壤富水性的要求。

2.2.2 基于功率谱属性与BP神经网络的土壤含水率定量探测

将主频、重心频率、边缘频率、频带能量、频率标准差、0～400 MHz 频带能量占比、400～600 MHz 频带能量占比作为BP 神经网络的输入层参数，输出层有1 个节点用于反演土壤含水率。

在物理模型实验所取得32 个土壤样本，22 个用于训练模型，10 个用于检验模型反演效果。通过凑试法不断对隐含层维数、节点数、学习效率和终止条件进行调整，结果表明在隐含层数为3 层，节点数为6 个，学习效率为0.1，网络训练1 000次时，预测模型达到最优。

通过训练成功的神经网络模型对测试的10 组数据进行预测。图5为网络输出回归分析线，反演土壤含水率与实际含水率的相关系数达0.936，表明模型输出含水率与实际含水率接近。图6 为BP 神经网络反演与实测含水率比较图，其中反演含水率与实际含水率的平均绝对误差为1.25%，最大绝对误差为2.6%，最小绝对误差为0.07%，均方根误差RMSE 为0.015。表明反演结果较好，基于功率谱属性参数与BP 神经网络结合的方法能够反映土壤含水率与探地雷达属性之间的非线性关系。

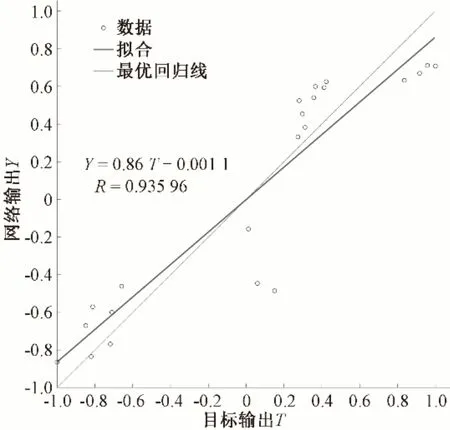
图5 网络输出回归分析线Fig.5 Regression analysis line of network output

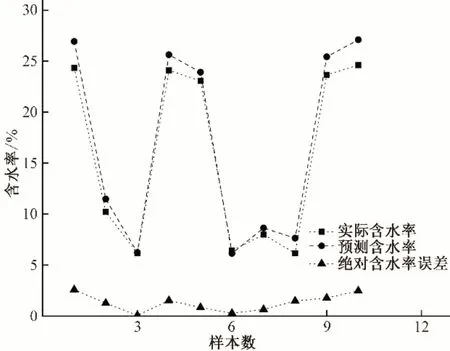
图6 BP神经网络反演与实测含水率误差分析图Fig.6 Error analysis plot of BP neural network inversion and measured water content in a physics experiment

2.3 实测验证

在物理实验结果分析及BP 神经网络预测土壤含水率中，仅是采用整道探地雷达信号研究利用功率谱预测土壤含水率的可行性，为实现利用功率谱预测不同深度上土壤含水率。首先利用时窗选取压缩变换技术截取0～80 cm 范围内的探地雷达信号，约24 ns，并将信号设置为1 024个数据点；然后采用滚动时间窗剖面技术将信号分为8 段，每段128 个数据点，每段时窗长度及深度范围分别为3 ns 及10 cm；最后利用AR 功率谱方法计算各深度上的探地雷达功率谱属性参数。将野外实验得到的探地雷达功率谱属性参数作为测试样本集，利用物理模型训练出的BP 神经网络对野外探测的土壤含水率进行识别与探测。并将BP 神经网络中得出预测结果与烘干法比较，验证结果如表7所示。

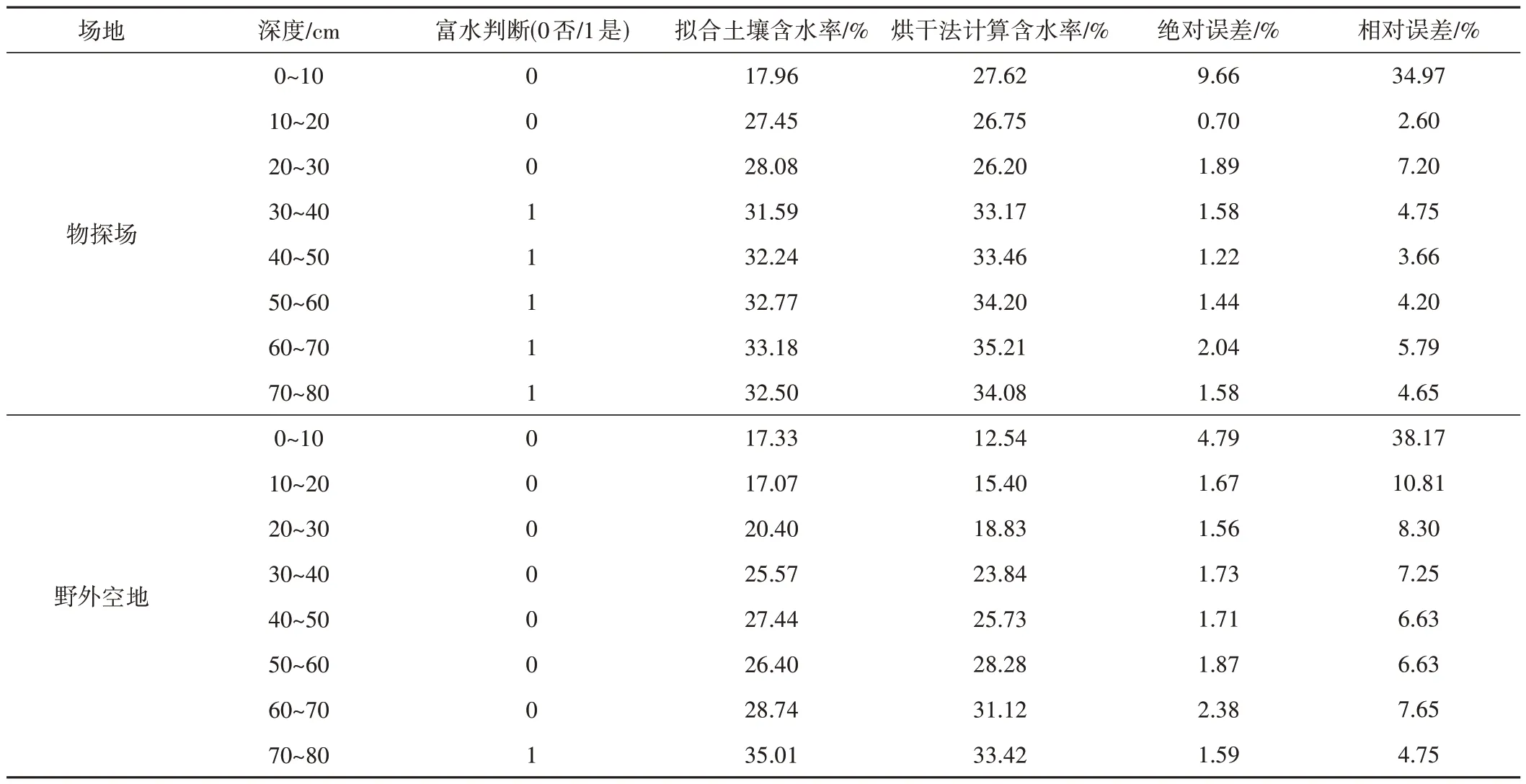
表7 野外实验探地雷达功率谱属性结合BP神经网络土壤含水率拟合对照表Tab.7 Comparison table of soil moisture estimation using field experiments, ground-penetrating radar power spectrum attributes, and BP neural network

在物探场及野外空地的16 组土壤含水率富水性识别中，出现一次错误，整体来说利用功率谱属性参数结合神经网络能成功的识别土层富水性。功率谱属性参数结合神经网络识别土壤含水率的方法均在0～10 cm的误差较大。10～80 cm范围内400 MHz 和900 MHz 绝对误差和相对误差分别在3%和10%以内，可以看出利用功率谱属性参数结合BP 神经网络方法反演土壤含水率精度较高。