涡发生器强化环形翅片管束管外传热的数值研究

陈 晨 虞 斌 方玮玮 凌卫平

（南京工业大学机械与动力工程学院）

随着我国经济的发展，节约能源、保护环境不仅是工业领域的任务，也与人们的日常生活息息相关。 随着餐饮行业市场化发展，天然气因储量大、安全、污染低等优点，成为餐饮业的主要能源。 我国部分地区餐饮业燃气灶产生的烟气大多不经环保装置处理直接排放至大气中，造成环境污染；烟气中含有的大量余热能源也得不到合理的回收利用，能源利用率低。 基于此，笔者提出了一套集制备热水、蒸汽和热风于一体的大型厨房余热回收再利用系统，该系统参照工业工程中常用的烟气余热回收方案，针对气体换热效率低的问题，采用分离式热管换热器作为主要的换热装置， 通过蒸发段来提取燃料燃烧后的高温余热，再由两个冷凝段释放热量达到余热回收并利用的目的。

热管内部传热通过工质相变实现，传热效率极高，而外部则是通过对流换热来实现的，由于烟气的对流换热系数较小，因此，笔者通过在环形翅片上增加纵向涡发生器（LVGs）来强化烟气侧的传热。 目前国内外学者对LVGs有大量的研究。 赵兰萍等在平翅片上添加三角形小翼，通过优化小翼位置角度来提升翅片管的换热效率［1］。曾卓雄等研究了H型翅片管上增添涡发生器后的流动特性，随着发生器迎风角度的增大，温差、压损及换热因子等均逐渐增大，但综合性能则是先增大后减小［2］。 王翠华等采用CFD模拟，对螺旋通道内A形翼和B形翼两种组合涡发生器进行比较，两者均能强化传热，且B形翼综合换热性能更好，在此基础上，通过研究涡发生器攻角和螺旋通道的曲率，来确定整体螺旋通道的最优综合换热性能［3，4］。 唐凌虹和曾敏在矩形通道内布置矩形翼、三角形翼及椭圆支柱的不同组合方式以此来强化光通道的换热性能， 研究表明CFU式三角形翼与椭圆支柱组合能提供最优的综合换热性能［5］。KE Z Q等采用图像法来分析动态壁面干扰引起的纵向涡，发现矩形通道的高度及LVGs纵横比是影响不同LVGs有效性的两个最关键因素［6］。

笔者将加装纵向涡发生器的翅片管束与光翅片管进行比较，并研究涡发生器相对位置对环形翅片热管管束流动及传热特性的影响。

1 数值模拟方法

1.1 物理模型

环形翅片管束的基本尺寸为管外径18 mm，翅片外径43 mm，翅片厚度0.8 mm，翅片间隙6 mm，共11排管，管束采取叉排排列方式，横向管间距为52 mm，纵向管间距为45 mm（图1）。 因蒸发段管束模型尺寸较大，故结合管束具有几何周期性的特点，截取高度6 mm，宽度26 mm的计算流体域（图2），流体域为天然气烟气。

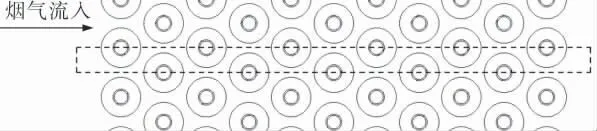
图1 环形翅片管束示意图

图2 物理模型计算流体域

在数值模拟过程中，对模型作如下几点简化和假设：假设流体为定常不可压缩流动；忽略重力因素；假设管壁为恒定壁温，因为热管工质是通过相变来实现传热的，因此壁面温度可认为是均匀的［7］；假设环形翅片与管壁恒定导热性且不考虑热辐射影响；为减弱出口回流现象，提升入口出口的流速均匀性，现将计算流体域的入口和出口均延长10倍的翅片外径。

1.2 数学模型

Fluent是建立在流体力学基本控制方程基础之上的，且流体的流动也受连续性方程、动量方程、能量守恒方程控制。 三大方程的数学形式（不可压缩流动）如下：

式中 cp——定压比热容；

p——流体微元上的压力；

ST——流体黏性在流动过程中机械能转化为热能部分；

T——温度；

λ——流体传热系数；

ρ——流体的密度；

υ——流体的运动黏度。

1.3 边界条件及数据处理

边界条件设置为：入口为速度入口，温度为673 K，出口为压力出口，管壁温度设为恒壁温，前5排管壁温为471 K，后6排管壁温为414.6 K。因为热管管束实际尺寸较大，为了提高数值模拟的计算效率，对整体模型截取计算流体域，计算流体域左右面设置为对称边界条件，上下面设置为周期性边界条件。

Fluent湍流模型选择SST-ω模型，此模型近壁面处理较好，近壁面处采用k-ω，主流区采用k-ε，通过转换方程进行转换，且SST模型是简化的BSL模型，一定程度上减小了计算量；压力速度耦合采用SIMPLEC求解方法，压力、动量、湍流动能等都采用二阶迎风格式离散，残差均设置为10-6。

所得数据按下式进行处理：

式中 AH——翅片管的总传热面积；

Amin——最小流量截面面积；

D——管束外径；

f——阻力因子，表征流体阻力特性；

f0——光翅片时阻力因子；

h——对流换热系数；

Nu——努塞尔数，表征流体对流换热强弱；

Nu0——光翅片时努塞尔数；

q——热流密度；

tin、tout、tw——进、出口及管壁温度；

Δp——压降；

ΔT——对数平均温差；

um——最小截面处流速。

其中，PEC为综合评价因子，能综合考虑换热和阻力因素，PEC大于1则表征强化传热具有意义，小于1则传热恶化［8］。

1.4 网格无关性检验及模型验证

以光翅片为例， 对计算流体域进行网格划分， 分别划分33万、73万、124万和170万网格，并在风速为2 m/s工况下进行数值模拟，所得努塞尔数及误差见表1。 由表1中数据可见，124万网格与170万网格数下误差仅相差0.48%， 因此选用124万网格进行模拟，既能保证计算的准确性也提升了计算机的运算效率。

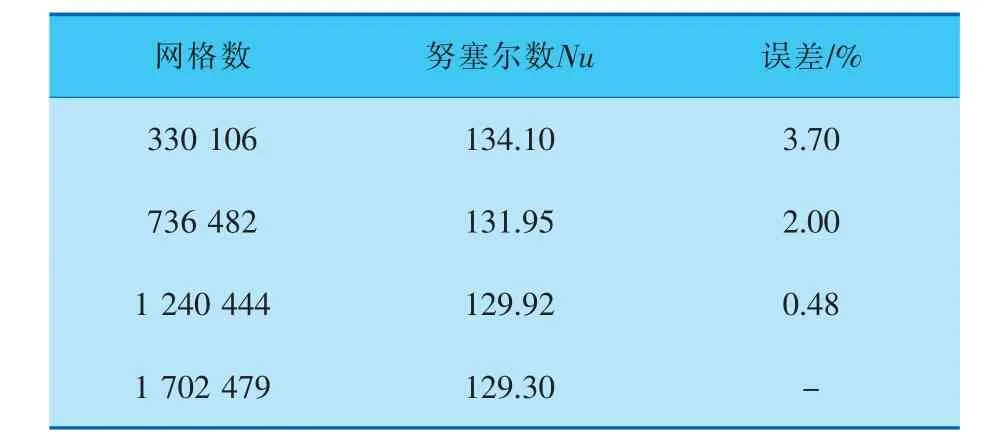
表1 光翅片不同网格数下的努塞尔数及误差

为了验证所选模型的准确性，将模拟结果与文献［9］中圆翅管束实验传热关联式所得结果进行比较，结果如图3所示。 通过关联式计算得到的努塞尔数与笔者的数值模拟值相对误差均在20%以内，且变化趋势相似，可认为该模型能有效地反映流体流动传热特性，证明模型可靠［10］。

图3 实验关联式与文中模拟结果对比

2 结果与讨论

纵向涡发生器的布置及安装方式如图4所示，图4a为内八型摆放形式矩形涡发生器，图4b为外八型摆放形式矩形涡发生器，图4c为内八型摆放形式角矩形涡发生器。 涡发生器的尺寸长度为6 mm，高度H=3.5 mm，厚度为1.5 mm，采用极坐标定位方式，以管中心为极点，纵向涡发生器中心点到极点的距离为极径r，极径与水平的夹角作为极角α。 笔者通过数值模拟方法对涡发生器进行选型和摆放形式选择，研究涡发生器相对位置对流体流动换热性能的影响，强化翅片管束的换热性能。

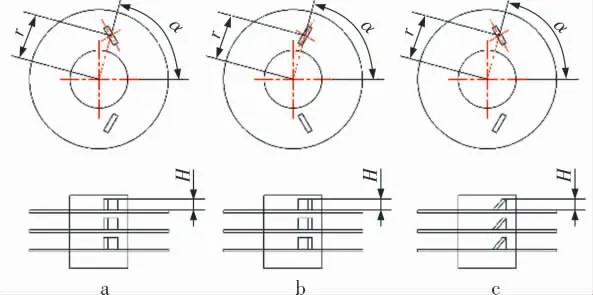
图4 涡发生器结构示意图

2.1 涡发生器流动换热性能比较

为了更好地强化翅片管束的换热能力，对上文提到的3种摆放形式的纵向涡发生器进行选型。 控制涡发生器在光翅片上的相对位置为极径r=14 mm，极角α=75°，迎风夹角为60°，且风速为3 m/s，对环形光翅片加装矩形涡发生器，角矩形涡发生器以及发生器摆放形式的模型进行数值模拟后，与光翅片管束进行对比，得到努塞尔数Nu、阻力因子f和综合评价因子PEC，如图5所示。

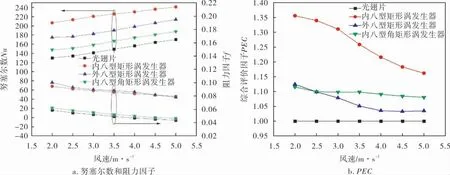
图5 不同涡发生器及摆放形式Nu、f和PEC的影响

分析图5可知， 内八型摆放的矩形涡发生器所得的努塞尔数最大，即换热性能最好，相较于光翅片Nu提升了42%～58%。其次为外八型摆放的矩形涡发生器和内八型摆放的角矩形涡发生器。阻力因子矩形涡发生器明显大于光翅片和角矩形涡发生器， 角矩形相较于光翅片提升了5.3%～6.6%；矩形涡发生器提升了近一倍，主要是因为矩形涡迎风面积比角矩形大了一倍，所以对流体的阻力也就更大。 阻力因子呈下降趋势是因为流体碰撞涡发生器的形体阻力是一定的，但随着流速的增大， 导致形体阻力占总压降比值变小，使得阻力因子呈下降趋势。 由图5b可知，内八型摆放形式矩形涡发生器的综合评价因子提升了16.2%～35.6%， 虽然内八摆放的矩形涡发生器产生的流动阻力要大于角矩形的，但其产生的扰动提升的换热性能要远大于阻力的影响，所以强化换热相较于其他两种涡发生器形式更有优势。

因每排管束后产生的涡旋效果类似， 故图6为截取第3排管管后1 mm处纵向截面上的速度矢量图， 能够有效反映纵向涡发生器对流体的扰动。 图中展示了管束的纵向涡，内八型矩形涡发生器（图6c）产生了4个纵向涡旋，相较于其他模型产生的涡旋更多，强度更强，涡旋冲刷流体边界层，使边界层减薄，其他3个计算模型产生的涡旋数量和强度要低于该模型（图6c）。 图7反映了内八型矩形涡发器纵向截面上的二次流强度，使上下冷热流体充分掺混，在翅片换热区域纵向冲刷换热边界层，因此内八型摆放形式矩形涡发生器换热性能更佳，努塞尔数提升更明显。

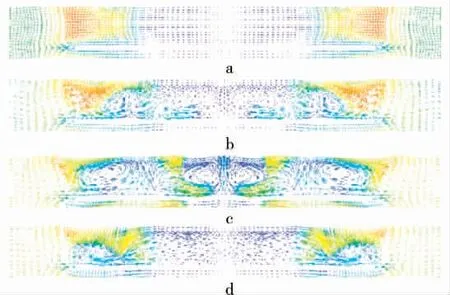
图6 不同模型纵向截面矢量图

图7 内八型矩形涡发生器纵向截面二次流强度云图

图8为4种模型流线图和速度云图，反映了计算流体域在z轴3 mm处流体流向和y方向上的速度云图。 由图可知，光翅片后形成了两个很大的涡旋回流区，流速低且具有滞留特性，导致该区域的对流换热能力相对较弱。 加装内八型矩形涡发生器（图8c）时，高速区的流体由矩形发生器引流，冲刷管后低速回流区的涡旋，使涡旋明显缩小， 发生器后形成了4个小涡旋， 使冷热流体掺混，提升了流体与管束之间的换热驱动力，此模型加剧流体的扰动和掺混，因此努塞尔数提升最大。 图8b、d所示模型涡发生器对流体有一定的扰动作用，但对管束后低速回流区的涡旋削减能力相较于图8c较弱，所以努塞尔数相对较低，强化换热能力较弱。

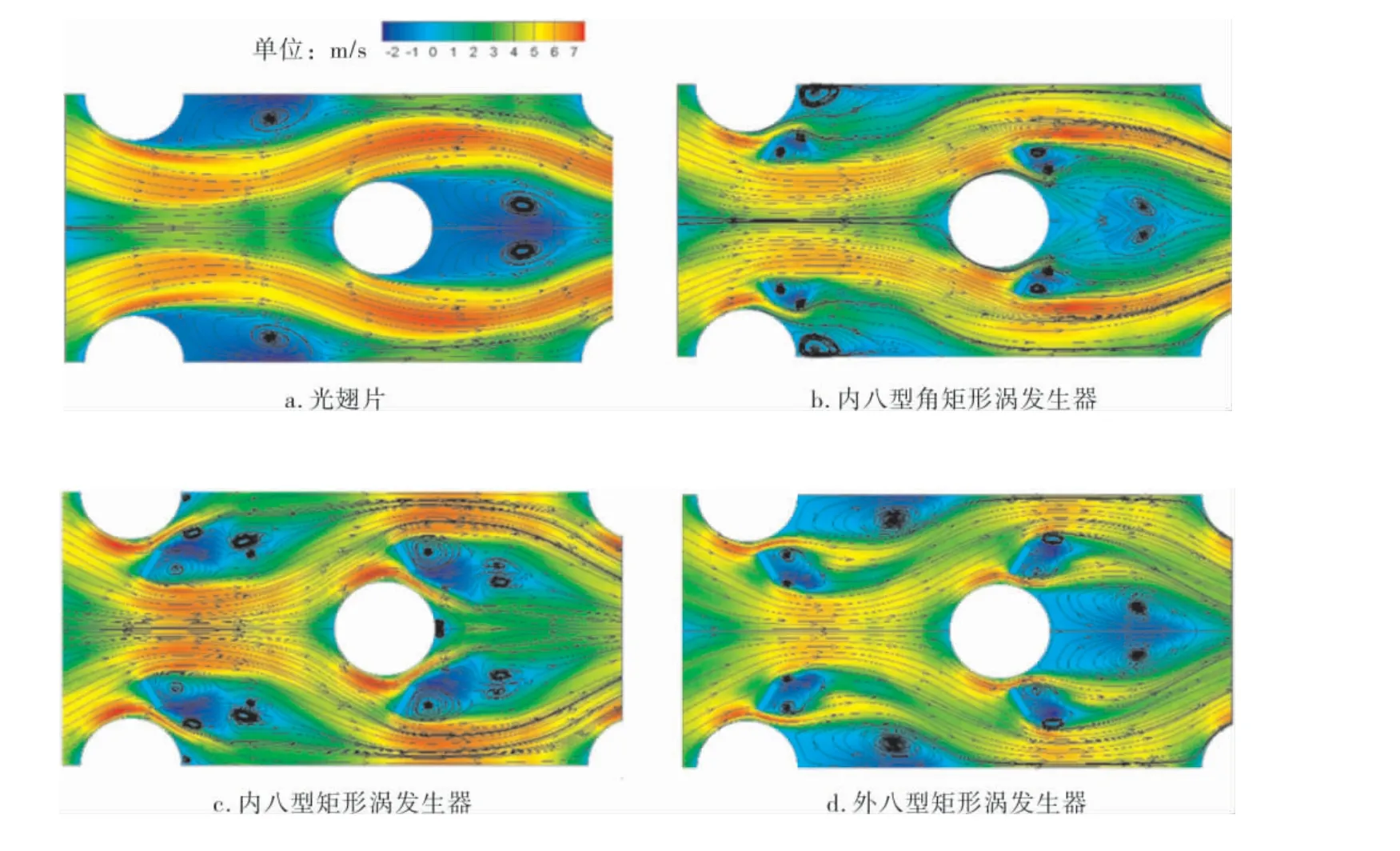
图8 不同模型横向截面流线图与速度云图

图9为不同模型横向截面的温度云图， 内八型矩形涡发生器 （图9c） 横截面的平均温度为558.7 K，无发生器（图9a）的平均温度为571.5 K，通过云图可直观地看出内八型矩形涡发生器对冷热流体的掺混和换热相较于其他模型更强，使高温流体能够更均匀地与低速回流区的低温换热面进行对流换热，流体流出时温度更低。

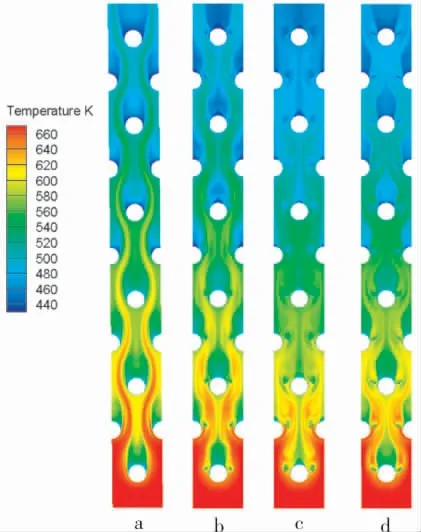
图9 不同模型横向截面温度云图

2.2 极径对管束流动传热性能指标分析

由上节选型研究讨论，最终选取内八型摆放形式的矩形涡发生器作为位置优化对象。

控制矩形涡发生器的迎风夹角为60°， 极角α=75°，研究对比了不同极径r（14、16、18 mm）下装有涡发生器的翅片和光翅片的流动传热特性。

如图10所示，随着风速的增加，不同极径的涡发生器努塞尔数均有所提升，这是因为速度增加，冲刷减薄了边界层厚度，降低了边界层热阻，提升了换热能力。 在相同风速下， 极径为14 mm时，努塞尔数最高，其次为极径16 mm，极径18 mm时的物理模型。 当矩形涡发生器相对位置在极径14 mm时， 相较于光翅片努塞尔数提升了41.9%～58.6%，换热能力提升最显著。这是因为极径小，矩形涡发生器更靠近管束，使得高速旁通区流体经发生器冲刷管束后的低速回流区；涡发生器距离管束越近则压缩管后涡旋能力越强。

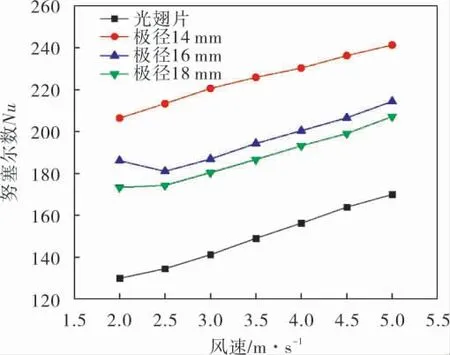
图10 不同极径对涡发生器传热性能的影响

如图11所示，3种位置PEC均大于1，说明该方式有利于强化传热。 在相同风速下，矩形涡发生器在极径为14 mm处时，综合评价因子最高，相较于光翅片提升了16.2%～35.6%， 强化了环形翅片管的流动换热能力，PEC呈下降趋势是因为随着流速的增加，涡发生器产生流体湍动占比越来越小所造成的。

图11 不同极径对涡发生器综合性能的影响

2.3 极角对管束流动传热性能指标分析

控制矩形涡发生器的迎风夹角为60°， 极径r=14 mm，研究对比了不同极角α（60、75、90°）下装有矩形涡发生器的翅片和光翅片的流动传热特性。

如图12所示，管束的换热能力随风速的增加逐渐增强，在相同风速下，矩形涡发生器在环形翅片上的相对位置在极角为75°时， 努塞尔数最高，其次为极角60°和极角90°位置，这是因为在极角75°时，涡发生器正好处于管束的高速旁通区与低速回流区过渡区域上，在对流体进行扰乱的同时，将高速的流体引入低速回流区，压缩了低速回流区的涡旋， 提升了低速回流区的换热能力，所以努塞尔数最高；极角为90°时，涡发生器完全处于高速旁通区，只对流体产生了扰动，对管束后的低速回流区的涡旋压缩作用不大，所以换热能力为3个位置中最差。

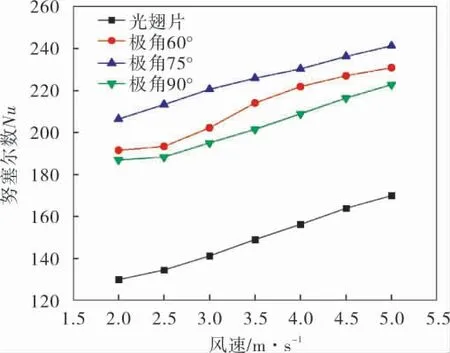
图12 不同极角对涡发生器传热性能的影响

由图13可知，极角为90°时，环形翅片管束整体的综合评价因子相较于其他两种位置最低，这是因为该位置对流体的阻力最大，而努塞尔数提升不大，造成综合换热能力不佳。 随着风速的增加，在风速低于3 m/s时，极角75°位置时要高于极角60°时的综合评价因子；当风速高于3 m/s时，则反之。 出现这一情况是因为， 虽然极角75°时，管束的努塞尔数最大，换热能力更强，但其产生的阻力却比极角为60°时要大，随着流速的增加，涡发生器相对位置在极角60°位置时， 从2.5 m/s开始，努塞尔数的提升速度加快，大于极角75°时的提升速度，且两者换热能力差距缩小，因此综合考虑阻力和换热双重因素的影响，极角60°风速3 m/s时超越极角75°时的综合评价因子。

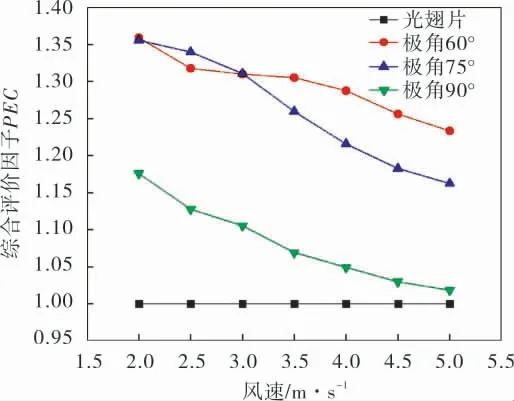
图13 不同极角对涡发生器综合性能的影响

3 结论

3.1 在环形光翅片上增加涡发生器能够提升流体的扰动，挤压低速回流区的涡旋，并且产生更多的纵向涡及二次流， 使冷热流体进行掺混，提升了环形翅片管束的综合换热性能。

3.2 由数值实验模拟可知，当矩形涡发生器和角矩形涡发生器为内八型摆放形式时，矩形涡发生器的综合换热能力要大于角矩形涡发生器；当矩形涡发生器在摆放形式上为内八型和外八型比较时，内八型摆放形式所得出的综合评价因子更高。

3.3 对内八型矩形涡发生器在环形光翅片上的相对位置进行研究讨论，以极坐标形式确定涡发生器在翅片上的相对位置。 研究发现，当矩形涡发生器中心位置在以翅片管中心为原点，极径为14 mm时，管束整体的综合换热性能最佳，综合换热能力提升了16.2%～35.6%；根据工况，当风速较低时，极角在75°位置时更佳，当风速较高时，极角为60°时更好。